Electricity Generation System with Piezoelectric Element Using Acoustic Radiation Energy

Hiroyuki Moriyama¹, Yuta Yamamura²

¹Department of Prime Mover Engineering, Tokai University, Hiratsuka, Japan.
²Course of Mechanical Engineering, Graduate School of Tokai University, Hiratsuka, Japan.

DOI: 10.4236/jpee.2018.610001                

Abstract

In this study, a circular plate that is installing a piezoelectric element at its center is adopted as energy-harvesting system and is subjected to a harmonic point force. Because this system cannot avoid the influence of its acoustic radiation, the influence is considered theoretically using the equation of plate motion taking into account its radiation impedance and is estimated by the electricity generation efficiency, which is derived from the ratio of the electric power in the electricity generation and the mechanical power supplied to the plate. As a result, the efficiency is suppressed by the acoustic radiation from the plate, so that the efficiencies are so different in whether to take into consideration the radiation impedance or not. Because those results are verified by the electricity generation experiment and radiation acoustic energy has a hopeful prospect for improving the performance of this system, mechanical-acoustic coupling is used to make the most of the acoustic energy. Therefore, a cylinder that has the above plates at both ends is also adopted as the electricity generation system and mechanical-acoustic coupling is caused between the plate vibrations and an internal sound field into the cylindrical enclosure by subjecting one side of each plate to a harmonic point force. Then, the effect of coupling is evaluated by comparing with the efficiencies in the electricity generation system of only plate. Specifically, because the radiation impedance increases with the plate thickness, i.e., with the natural frequency of the plate, it is demonstrated that the effect of coupling becomes remarkable with increasing the thickness on the electricity generation efficiency.

Keywords

Electricity Generation System, Piezoelectric Element, Radiation Impedance, Coupling

1. Introduction

Energy harvesting utilizes various energy sources, such as heat, wind, solar energies, and so on. Even among them, untapped vibration energy exists fully around us and technologies to be able to scavenge such energy are so significant. Although several methods to harvest the vibration energy have been proposed a lot, piezoelectric materials that can convert it into usable electric energy are taken up and electricity generation systems that are attaching the materials to host structures attract considerable attention. Because a simple cantilever beam is adopted generally as the host structure, it is comparatively easy to theoretically model it and to carry out the theoretical procedure model [1] . Then, the electricity generation system is regarded as one of promising energy sources. However, in order to actually use such a system, it is so significant to be able to recover electric energy more efficiently from vibration energy, because energy harvesting with piezoelectric elements is generally limited.

In such an energy-harvesting system, matching the load impedance with the input impedance is significant. Therefore, the variations in the maximum power have been considered by changing the resistance of the resistor by which the load impedance was characterized [2] [3] . Then to improve the modal equivalent stiffness ratio, modal electro-mechanical coupling coefficient, and modal piezoelectric voltage coefficient of a piezoelectric element attached to a beam, two mechanical impedance matching methods were proposed, and then they were derived from using spacers between the piezoelectric element and beam structure and from tuning for the size of the piezoelectric element [4] . In the case of the cantilever beam that was selected as the host structure, because the vibration characteristics were adjusted easily due to a tip mass and related directly to the efficiency (with respect to the tip mass), the influence of the size and position on electricity generation characteristics was considered [2] . In general, the rectangular strip shape is adopted as the host structure. However, because it is also possible to assume various shapes, electricity generation characteristics were compared in rectangular and triangular shapes, and it was verified that the performance of a triangular shape was superior to that of a rectangular shape [3] . Although vibrators have been used as vibration sources in almost all cases, fluttering caused by placing a plate into a flow was also employed. In that case, a small set of piezoelectric elements that consisted of one, two, or three pairs was used and the impact of these arrangements on nonlinear dynamics and energy harvesting efficiency was studied numerically and experimentally. Moreover, a parametric numerical study was carried out to determine the optimal arrangement [5] .

Naturally, the use of a large element or many elements is also a useful way to improve electricity generation characteristics. With respective to the above strip beam, the short sides should be enlarged to expand the adhesive area of piezoelectric elements. However, the strip beam must be regarded as a rectangular plate in case the flexural displacement along the short sides cannot be ignored because of their vibration modes. Not only rectangular plates, but also circular plates, are fundamental two-dimensional host structures. Therefore, a disk-type harvester that consisted of a rather thick base metal plate with two bimorph piezoceramic plates and a metal circumferential passive mass was introduced as a new energy harvester [6] .

However, a three-dimensional hexahedral acoustic cavity was adopted, and its walls were rigid, except the top one, which was a flexible aluminum plate. The plate was excited by a point force, and the piezoelectric element was bonded on its surface to suppress the plate vibration energy and internal acoustic energy that were amplified by mechanical-acoustic coupling. Then it was shown that the damping technique using a resistor-inductor shunt circuit, to which the piezoelectric element was connected, was very effective for the attenuation of the above vibration and acoustic energies in the low frequency range [7] . Moreover, the coupled FEM-BEM model was obtained by using a compatible mesh at the fluid-structure interface. The vibration reduction of an elastic plate backed by a closed acoustic cavity was considered as with Reference 7. On the other hand, the attenuation of the sound field emitted from a simply-supported plate in a half-space acoustic domain was simulated using the piezoelectric shunt system [8] .

In this study, a circular plate, on which a piezoelectric element is installed at its center, is adopted as the host structure and is subjected to a harmonic point force. As described above, in many cases, a cantilever beam is used as the host structure and an influence of its acoustic radiation has been able to be ignored on electricity generation characteristic. However, this system cannot avoid the influence derived from enlarging contact areas with the surrounding medium on both plate surfaces, so that harvesting acoustic energy radiated from the circular plate is one of important matters to improve electricity generation characteristics. In our previous work, some problems remained unsolved with respect to such an influence and the convergence of some theoretical solutions [9] . Therefore, the influence is considered theoretically using the equation of plate motion taking into account its radiation impedance and is estimated by the electricity generation efficiency, which is derived from the ratio of the electric power in the electricity generation and the mechanical power supplied to the plate, and then these results are verified by the electricity generation experiment. Then the convergence is considered enough in the theoretical procedure. On the other hand, to utilize such an acoustic radiation for energy-harvesting, a cylinder that has the above plates at both ends is also adopted as the electricity generation system and mechanical-acoustic coupling is caused between the plate vibrations and an internal sound field into the cylindrical enclosure by subjecting one side of each plate to a harmonic point force. Then the effect of coupling is evaluated by comparing with the efficiencies in the electricity generation system of only plate.

2. Analytical Method

2.1. Analytical Model

Figure 1 shows the analytical model that consists of a cavity with plates 1 and 2.

Figure 1. Configuration of analytical model.

It is assumed that both plates are supported by translational and rotational springs. These springs are distributed at constant intervals and the support conditions are determined by the translational spring stiffness T and the rotational spring stiffness R. The plates whose radius and thickness are denoted by r_c and h_c, respectively, have a Young’s modulus E_c and a Poisson’s ratio ν_c. Piezoelectric elements are installed at the centers of the plates and have radius r_p, thickness h_p, Young’s modulus E_p, and Poisson’s ratio ν_p. Then an electrode plate that is made of brass is sandwiched between the above plate and piezoelectric element and has radius r_b, thickness h_b, Young’s modulus E_b and Poisson’s ratio ν_b. The suffixes c, p, and b denote the circular plate, piezoelectric element, and electrode plate. On the other hand, the cylinder has the same radius as that of the plates and the sound field is formed inside the cavity via coupling with the plate vibrations. The length L is varied widely because the resonance frequency depends on the length. The boundary conditions are regarded as structurally and acoustically rigid at the lateral wall except the plates. The representative coordinates are radius r, angle θ between the planes of the plates and the cross-sectional plane of the cavity, and distance z along the cylinder axis. Plate 1 is excited by the periodic point force F at distance r₁ and angle θ₁ and its natural frequency is employed as the excitation frequency.

Because the suffixes 1 and 2 indicate Plates 1 and 2, the flexural displacements of the Plates 1 and 2 are denoted by w_c1 and w_c2 and those of the piezoelectric elements installed on the plates are denoted by w_p1 and w_p2, respectively. Their displacements are expressed by Equation (1) as suitable trial functions and have the plate mode $X_{nm}^s$ of Equation (2). The flexural displacements of the piezoelectric elements are identical to those of the plates, respectively, because it is assumed that the piezoelectric elements adhere completely to each circular plate through the electrode plate.

$\begin{array}{l}{w}_{c1}=w_{p1}={\displaystyle \underset{s=0}{\overset{1}{\sum }}{\displaystyle \underset{n=0}{\overset{\infty }{\sum }}{\displaystyle \underset{m=0}{\overset{\infty }{\sum }}{X}_{nm}^s{A}_{1nm}^s{\text{e}}^{\text{j}\left(\omega t+{\alpha }_1\right)}}}},\\ w_{c2}=w_{p2}={\displaystyle \underset{s=0}{\overset{1}{\sum }}{\displaystyle \underset{n=0}{\overset{\infty }{\sum }}{\displaystyle \underset{m=0}{\overset{\infty }{\sum }}{X}_{nm}^s{A}_{2nm}^s{\text{e}}^{\text{j}\left(\omega t+{\alpha }_2\right)}}}},\end{array}$ (1)

$X_{nm}^s=\sin \left(n\theta +s\text{π}/2\right){\left(r/r_c\right)}^m,$ (2)

where n and m are the circumferential and radial orders and s is symmetry index with respect to the vibration mode. $A_{1nm}^s$ and $A_{2nm}^s$ are coefficients to be determined and correspond to the amplitude of the flexural displacement. ω is the angular frequency of the harmonic point force acting on the plate and t is the elapsed time. α₁ and α₂ are the phases of the respective plate vibrations, here, α₁ is set to 0˚, and α₂ ranges from 0˚ to 180˚.

2.2. Modeling of Piezoelectric Part

To explain modelling of only the piezoelectric part of Plate 1, this section takes note of its stress ${\sigma }_{p1}$, strain ε_p1, electric displacement D₁, and electric field E₁ and their relationships are as follows:

$\left\{\begin{array}{c}{\sigma }_{p1}\\ D_1\end{array}\right\}=\left[\begin{array}{cc}{E}_p^E& -e^{\text{T}}\\ e& {\gamma }^{\epsilon }\end{array}\right]\left\{\begin{array}{c}{\epsilon }_{p1}\\ E_1\end{array}\right\}.$ (3)

$E_p^E$ signifies Young’s modulus when a electric field is constant and ${\gamma }^{\epsilon }$ indicates the dielectric constant when a strain is constant. Because electrical and mechanical characteristics of a piezoelectric element are related by the piezoelectric coupling coefficient e, these relationships are represented by Equation (3). The piezoelectric coupling coefficient becomes as follows:

$e=d_{31}{E}_P^E$, (4)

where d₃₁ is the piezoelectric strain constant, and here, electric field occurs in the normal direction of the in-plane strain.

Then the electric field E₁, which occurs in the above direction of the piezoelectric element, is expressed as follows:

$E_1=Y_{nm}{v}_1=-R_c{\stackrel{\dot{}}{q}}_1=\text{j}\omega B_{1nm}^s{e}^{\text{j}\left(\omega t+{\alpha }_1\right)}$ . (5)

v₁ is the voltage that occurs in the electric field. The electric potential across the piezoelectric element is constant since it is assumed that it does not reach the plate, so that Y_nm is defined as Equation (6). R_c is the overall resistance value in an electricity generation circuit. The magnitude ofthe electric charge q₁ depends on the coefficient $B_{1nm}^s$ that is determined in this analysis as with $A_{1nm}^s$ .

$Y_{nm}=\{\begin{array}{l}-1/h_p{h}_c/2<z<h_c/2+h_b+h_p,\\ 0h_c/2<z<h_c/2+h_b+h_p,\end{array}$ (6)

$q_1=B_{1nm}^s{\text{e}}^{\text{j}\left(\omega t+{\alpha }_1\right)}$ . (7)

To make the electro-mechanical equation concise, the elements $M_{1nm{m}^{\prime }}^s$ and $K_{1nm{m}^{\prime }}^s$ of the mass and stiffness matrices can be defined as

$M_{p1nm{m}^{\prime }}^s={\displaystyle {\int }_{V_{p1}}{\rho }_p{X}_{nm}^s{X}_{n{m}^{\prime }}^s\text{d}{V}_{p1}},$ (8)

$K_{p1nm{m}^{\prime }}^s={\displaystyle {\int }_{V_{p1}}{z}^2{X}_{nm}^s{}^{"}{E}_p^E{X}_{n{m}^{\prime }}^s{}^{"}\text{d}{V}_{p1}}.$ (9)

The index m' has a transposed relation to a radial order m. The respective elements of electro-mechanical coupling and capacitance matrices are denoted by β₁ and C_p1 and they are defined as follows:

${\beta }_1=-{\displaystyle {\int }_{V_{p1}}z{\rho }_p{X}_{nm}^{s}e{Y}_{n{m}^{\prime }}\text{d}{V}_{p1}},$ (10)

$C_{p1}={\displaystyle {\int }_{V_{p1}}{Y}_{nm}{\gamma }^{\epsilon }{Y}_{n{m}^{\prime }}^s\text{d}{V}_{p1}}.$ (11)

2.3. Governing Equations of Electromechanical-Acoustic Coupling

Here, electro-mechanical coupling is based on the above several relationships, and then mechanical-acoustic coupling is also induced from the relationships between the vibrations of both plates and the sound field into the cylindrical cavity. Resultantly, this electricity generation phenomenon takes place under the situation of electro-mechanical-acoustic coupling, so that the plate vibrations, the sound field, and the electricity generation are governed by the following Equations (12) and (13), respectively [9] :

$\begin{array}{l}{\displaystyle \underset{m^{\prime }=0}{\overset{\infty }{\sum }}[K_{c1nm{m}^{\prime }}^s\left(1+\text{j}{\eta }_c\right)+K_{p1nm{m}^{\prime }}^s\left(1+\text{j}{\eta }_p\right)+K_{b1nm{m}^{\prime }}^s\left(1+\text{j}{\eta }_b\right)\underset{}{\underset{}{}}}\\ -{\omega }^2\left(M_{c1nm{m}^{\prime }}^s+M_{p1nm{m}^{\prime }}^s+M_{b1nm{m}^{\prime }}^s\right)\\ +r_c{F}_{sn}\left\{T+\left(\frac{m}{r_c}\right)\left(\frac{m^{\prime }}{r_c}\right)R\right\}]A_{1n{m}^{\prime }}^s{\text{e}}^{\text{j}{\alpha }_1}-{\displaystyle \underset{m^{\prime }=0}{\overset{\infty }{\sum }}{\beta }_1{v}_1^{-}{B}_{1n{m}^{\prime }}^s{\text{e}}^{\text{j}{\alpha }_1}}=F_{nm}^s{\text{e}}^{\text{j}{\alpha }_1}-S_{1nm}^s,\end{array}$ (12)

$\begin{array}{l}{\displaystyle \underset{m^{\prime }=0}{\overset{\infty }{\sum }}[K_{c2nm{m}^{\prime }}^s\left(1+\text{j}{\eta }_c\right)+K_{p2nm{m}^{\prime }}^s\left(1+\text{j}{\eta }_p\right)+K_{b2nm{m}^{\prime }}^s\left(1+\text{j}{\eta }_b\right)\underset{}{\underset{}{}}}\\ -{\omega }^2\left(M_{c2nm{m}^{\prime }}^s+M_{p2nm{m}^{\prime }}^s+M_{b2nm{m}^{\prime }}^s\right)\\ +r_c{F}_{sn}\left\{T+\left(\frac{m}{r_c}\right)\left(\frac{m^{\prime }}{r_c}\right)R\right\}]A_{2n{m}^{\prime }}^s{\text{e}}^{\text{j}{\alpha }_2}-{\displaystyle \underset{m^{\prime }=0}{\overset{\infty }{\sum }}{\beta }_2{v}_2^{-}{B}_{2n{m}^{\prime }}^s{\text{e}}^{\text{j}{\alpha }_2}}=S_{2nm}^s.\end{array}$ (13)

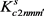$K_{c1nm{m}^{\prime }}^s$, $K_{b1nm{m}^{\prime }}^s$ and, $K_{b2nm{m}^{\prime }}^s$ are stiffness matrix elements in the end plates and $M_{c1nm{m}^{\prime }}^s$, $M_{b1nm{m}^{\prime }}^s$ and $M_{c2nm{m}^{\prime }}^s$, $M_{b2nm{m}^{\prime }}^s$ are mass matrix elements in the electrode plates, respectively. These are elements of the symmetrical matrices, since the index m' has a transposed relation to m, as with $M_{p1nm{m}^{\prime }}^s$ and $K_{p1nm{m}^{\prime }}^s$ . η_c, η_p, and η_b signify the structural damping factors of the end plate, piezoelectric element, and electrode plate, respectively. Then F_sn is a coefficient that is determined by the indices n and s and $F_{nm}^s$ is a load vector that is applied to Plate 1 as the point force. On the other hand, $S_{1n{m}^{\prime }}^s$ and $S_{2n{m}^{\prime }}^s$ matrices are the acoustic excitation terms, which signify coupling between each plate vibration and the internal sound field, and both matrices are including $A_{1nm}^s$ and $A_{2nm}^s$ . The details of F_sn and the respective elements $F_{nm}^s$, $S_{1nm}^s$, and $S_{2nm}^s$ of the vector and matrices are as follows:

$F_{sn}=\{\begin{array}{l}\text{π},\text{at}n\ne 0,\hfill \\ 0,\text{at}n=0\text{and}s=0,\hfill \\ 2\text{π},\text{at}n=0\text{and}s=1,\hfill \end{array}$ (14)

$F_{nm}^s={\displaystyle {\int }_{A_1}F\delta \left(r-r_1\right)\delta \left(\theta -{\theta }_1\right)X_{nm}^s\text{d}{A}_1},$ (15)

$S_{1nm}^s={\displaystyle {\int }_{A_1}{P}_s{X}_{nm}^s\text{d}{A}_1},S_{2nm}^s={\displaystyle {\int }_{A_2}{P}_s{X}_{nm}^s\text{d}{A}_2}.$ (16)

Here, the point force is expressed by performing Equation (12) including the delta function δ on Plate 1, whose area is denoted by A₁. P_s is the sound pressure at an arbitrary point on both plates, and A₂ signifies the area of Plate 2.

On the other hand, the electricity generation behaviors of the piezoelectric elements are also governed by the following Equations (17) and (18), respectively:

${\displaystyle \underset{m^{\prime }=0}{\overset{\infty }{\sum }}{C}_{p1}^{-1}{\beta }_1{A}_{1n{m}^{\prime }}^s}={\displaystyle \underset{m^{\prime }=0}{\overset{\infty }{\sum }}\left(\text{j}\omega R_p+C_{p1}^{-1}\right)B_{1n{m}^{\prime }}^s},$ (17)

${\displaystyle \underset{m^{\prime }=0}{\overset{\infty }{\sum }}{C}_{p2}^{-1}{\beta }_2{A}_{2n{m}^{\prime }}^s}={\displaystyle \underset{m^{\prime }=0}{\overset{\infty }{\sum }}\left(\text{j}\omega R_p+C_{p2}^{-1}\right)B_{2n{m}^{\prime }}^s}.$ (18)

The relationships between $A_{1nm}^s$ and $B_{1nm}^s$ and between $A_{2nm}^s$ and $B_{2nm}^s$ are applied to Equations (12) and (13), respectively, and these coefficients can be derived by solving the above simultaneous equations. However, Plate 1 is excited by the point force of its natural frequency and the behavior is assumed to be harmonic, so that ${\text{e}}^{\text{j}\omega t}$ could be eliminated in Equations (12) and (13). Moreover, ${\text{e}}^{\text{j}\left(\omega t+{\alpha }_1\right)}$ and ${\text{e}}^{\text{j}\left(\omega t+{\alpha }_2\right)}$ could be also eliminated in Equations (17) and (18), respectively.

In the case of the electricity generation by means of only the vibration of Plate 1, i.e., in the condition of removing the cylinder and Plate 2 in Figure 1, $A_{1nm}^s$ and $B_{1nm}^s$ are obtained from solving simultaneously Equations (12) and (17). However, the acoustic excitation term $S_{1n{m}^{\prime }}^s$ is deleted in Equation (12) because of not taking into consideration mechanical-acoustic coupling. Then the flexural displacement w_c1 is calculated by substituting $A_{1nm}^s$ for Equation (1) and the mechanical power P_m to be supplied to Plate 1 is obtained from the relationships between its flexural displacement and the force at the excited point. The voltage v₁ is calculated by substituting $B_{1nm}^s$ for Equations (5) and (7), when the piezoelectric element generates electricity by the vibration of Plate 1. Although the electric power P_e is obtained from the product of its voltage v₁ and the electric current corresponding to v₁, the derivation of its electric current is explained in Section 4.2.

2.4. Radiation Impedance of Vibration Circular Plate

Plate 1 must receive the reaction force from the circumambient medium, being excited by the point force. In other words, this means that the radiation impedance of Plate 1 increases by means of the amount of the reaction. Such an increase is taken up in this section. To simplify the problem, it is assumed that the acoustic radiation is caused by a circular piston source, which is derived from Plate 1 excited by the velocity amplitude U₀. First, velocity potential df at Point P on the x-axis of Plate 1 is considered, and it is derived based on assuming that it is caused by plate vibration on an arbitrary minute area dA₁, as shown in Figure 1. Then, the velocity potential f is obtained from the surface integral in the entire area of Plate 1 as follows:

$\varphi =\frac{U_0{\text{e}}^{\text{j}\omega t}}{2\text{π}}{\displaystyle {\int }_0^{2\text{π}}\text{d}\psi }{\displaystyle {\int }_0^H{\text{e}}^{-\text{j}kh}\text{d}h},$ (19)

$H=x\cos \psi +\sqrt{r_c^2-x^2{\sin }^2\psi }.$ (20)

Here, k is the wavelength constant, and the segment H can be expressed as Equation (20), so that Equation (19) becomes the following equation.

$\varphi =\text{j}\frac{U_0{\text{e}}^{\text{j}\omega t}}{k\text{π}}{\displaystyle {\int }_0^{\text{π}}\left\{{\text{e}}^{-\text{j}k\left(x\cos \psi +\sqrt{r_c^2-x^2{\sin }^2\psi }\right)}-1\right\}\text{d}\psi },$ (21)

$x\cos \psi =\mu ,\sqrt{r_c^2-x^2{\sin }^2\psi }=\chi .$ (22)

In addition, according to variables transformations of Equation (22), the integrand of Equation (21) is expanded in the power series of (μ + χ), and f becomes the following equation.

$\begin{array}{c}\varphi =\frac{U_0{\text{e}}^{\text{j}\omega t}}{\text{π}}{\displaystyle {\int }_0^{\text{π}}[\left\{\frac{\left(\mu +\chi \right)}{1!}-\frac{k^2{\left(\mu +\chi \right)}^3}{3!}+\frac{k^4{\left(\mu +\chi \right)}^5}{3!}-\cdots \right\}}\\ -\text{j}\left\{\frac{k{\left(\mu +\chi \right)}^2}{2!}-\frac{k^3{\left(\mu +\chi \right)}^4}{4!}+\frac{k^5{\left(\mu +\chi \right)}^6}{6!}-\cdots \right\}]\text{d}\psi ,\end{array}$ (23)

$P_s=\text{j}\omega {\rho }_a\varphi$, (24)

where $P_s$ is the sound pressure, and ρ_a is the medium density.

Because f is calculated from the integral of each term in Equation (23), P_s at Point P is obtained by substituting it into Equation (24). Because this sound pressure behaves as a reaction force to Point P, the total reaction forces on the respective surfaces are induced from the surface integral of P_s in the entire area of Plate 1, as shown in Figure 1. For instance, F_ra is expressed by the following equation.

$\begin{array}{c}{F}_{ra}{\text{e}}^{\text{j}\left(\omega t+{\alpha }_a\right)}={\rho }_{s}c{U}_0{\text{e}}^{\text{j}\left(\omega t+{\alpha }_a\right)}[\text{π}{r}_c^2\left\{\frac{{\left(2k{r}_c\right)}^2}{2\times 4}-\frac{{\left(2k{r}_c\right)}^4}{2\times 4^2\times 6}+\frac{{\left(2k{r}_c\right)}^6}{2\times 4^2\times 6^2\times 8}-\cdots \right\}\\ +\frac{\text{j}}{k^2}\left\{\frac{{\left(2k{r}_c\right)}^3}{1\times 3}-\frac{{\left(2k{r}_c\right)}^5}{1\times 3^2\times 5}+\frac{{\left(2k{r}_c\right)}^7}{1\times 3^2\times 5^2\times 7}-\cdots \right\}]\\ =\text{π}{r}_c^2{\rho }_{s}c{U}_0{\text{e}}^{\text{j}\left(\omega t+{\alpha }_a\right)}\left[\left\{1-\frac{{\text{J}}_1\left(2k{r}_c\right)}{k{r}_c}\right\}+\text{j}\frac{{\text{S}}_1\left(2k{r}_c\right)}{k{r}_c}\right],\end{array}$ (25)

where α_a is the phase and J₁ and S₁ are the Bessel function of the first kind and the Struve function, respectively. Because the sound fields are considered symmetric on both sides of Plate 1, F_rb can be expressed by Equation (25) where the phase α_b is adopted instead of α_a.

By taking up the analytical model in which the cylinder and Plate 2 are removed (i.e., the analytical model of only Plate 1), and reflecting the above reaction forces to the motion equation of Plate 1, Equation (12) can be rewritten as follows:

$\begin{array}{l}{\displaystyle \underset{m^{\prime }=0}{\overset{\infty }{\sum }}[K_{c1nm{m}^{\prime }}^s\left(1+\text{j}{\eta }_c\right)+K_{p1nm{m}^{\prime }}^s\left(1+\text{j}{\eta }_p\right)+K_{b1nm{m}^{\prime }}^s\left(1+\text{j}{\eta }_b\right)\underset{}{\underset{}{}}}\\ -{\omega }^2\left(M_{c1nm{m}^{\prime }}^s+M_{p1nm{m}^{\prime }}^s+M_{b1nm{m}^{\prime }}^s\right)\\ +r_c{F}_{sn}\left\{T+\left(\frac{m}{r_c}\right)\left(\frac{m^{\prime }}{r_c}\right)R\right\}]A_{1n{m}^{\prime }}^s{\text{e}}^{\text{j}{\alpha }_1}-{\displaystyle \underset{m^{\prime }=0}{\overset{\infty }{\sum }}{\beta }_1{v}_1^{-}{B}_{1n{m}^{\prime }}^s{\text{e}}^{\text{j}{\alpha }_1}}\\ =F_{nm}^s{\text{e}}^{\text{j}{\alpha }_1}-F_{ra}{\text{e}}^{\text{j}{\alpha }_a}+F_{rb}{\text{e}}^{\text{j}{\alpha }_b}\text{.}\end{array}$ (26)

To estimate the influence of these reaction forces on electricity generation characteristics, the above equation is solved simultaneously with Equation (17).

3. Experimental Apparatus and Method

In the experimental study, the experimental apparatus, which consists of a steel cylinder with circular aluminum end plates, emulates the analytical model, as shown in Figure 2(a). Concretely, the end plates have the radius r_c of 153 mm and their thicknesses are changed as in 2.0, 2.5, 3.0, and 4.0 mm. The cylinder has the inner radius same as the plate radius and its length L ranges from 500 to 1000 mm. The point force is applied to Plate 1 by a small vibrator, the amplitude F is set to 1 N, and the excitation is carried out near the natural frequency of the (0, 0) mode. Then the position of the point force r₁ is 61 mm and is set to r₁/r_c = 0.4 by means of normalizing by radius r_c.

The acceleration a₁ is measured in close proximity of the excitation position and the mechanical power P_m supplied to Plate 1 by the small vibrator is estimated from the relationship between F and a₁. The acceleration a₂ of Plate 2 is also measured simultaneously at the same position as a₁ on Plate 2. Then the phase difference between the plate vibrations is considered from the measurements of a₁ and a₂, resulting in significant effects on the mechanical-acoustic coupling. However, the coupling situation is estimated from not only the phase difference but also the internal acoustic characteristics. Therefore, although the sound pressure level in the cavity is measured using condenser microphones, a probe tube is attached to each microphone not to prevent the sound wave propagation inside the cavity. Because the sound pressure level is maximized near both end plates when the sound field becomes resonant, the tips of the probe tubes are located near the plates and the cylinder wall.

The piezoelectric element used to perform the electricity generation experiment is comprised of a circular piezoelectric part constructed of ceramics and a circular electrode part constructed of brass. The piezoelectric and ceramics parts have radiuses r_p and r_b of 12.5 and 17.5 mm and thicknesses h_p and h_b of 0.23 and 0.30 mm, respectively. The piezoelectric elements are installed at the centers of both plates as with the analytical model. The electric power P_e is generated by the expansion and contraction of the piezoelectric element on the plate surface derived from the flexural vibration of the plate and is obtained from the resistance circuit, which is composed of three resistors having resistances R_v, R_i, and R_c, as shown in Figure 2(b). R_v and R_i are the resistances of the voltmeter and ammeter, which are incorporated into the power meter, and are 2 MΩ and 2 mΩ, respectively. However, R_c is the resistance of the resistor to consume the generated electric power and is mainly 97.5 kΩ, and then the resistor is connected outside the power meter.

Before the experiment, the electric power and other data were also observed without the cylinder (i.e., in the electricity generation under the vibration of only Plate 1). However, the sound pressure levels were measured on both sides of Plate 1, as shown in Figure 3. Thus, the influence of the radiation impedance on the electricity generation characteristics was determined from the phase difference between both radiated sound fields. Moreover, the effects of mechanical-acoustic coupling on energy harvesting was estimated in comparison with those with the cylinder.

Figure 2. Configuration of experimental apparatus: (a) measurement system and (b) electrical circuit of energy-harvesting device.

Figure 3. Configuration of experimental apparatus to measure phase difference.

4. Results and Discussion

4.1. Theoretical and Experimental Conditions

The plate and piezoelectric element were the same as the experimental apparatus in the respective dimensions, and had the mechanical and electrical properties shown in Table 1. The plate radii r_c were constant at 153 mm, and the plate thickness h_c ranged from 1.5 to 4.5 mm. The support conditions of the plates, which had flexural rigidity $D\left[=E{h}_c^3/\left\{12\left(1-{\nu }^2\right)\right\}\right]$, are expressed by the nondimensional stiffness parameters $T_n\left(=T{r}_c^3/D\right)$ and $R_n\left(=R{r}_c/D\right)$ . These values were identical for both plates. If R_n ranged from 0 to 10⁸ when T_n was 10⁸, the support condition could be assumed from a simple support to a clamped support. Although almost all conditions adopted T_n = 10⁸ and R_n = 10¹ to get closer to the experimental support condition, R_n changed in a part of the analysis. Plate 1 was subjected to the point force F that was set to 1 N, as with the excitation experiment. Then, the position was almost located at r₁/r_c = 0.4, whereas, r₁/r_c changed in a part of the analysis.

With respect to the electricity generation system of only Plate 1, which does not have the cylinder and Plate 2 in Figure 1, the theoretical voltage v₁ is indicated with changing the excitation frequency f in Figure 4, and it peaked at f = 279 Hz, which corresponds to the natural frequency of Plate 1. The experimental results are also exhibited in this figure, and they were measured by changing the length L_S of a stick exciting Plate 1. Both voltages had each peak taking place at f = 245 and 231 Hz when L_S was 13.6 and 75.0 mm, respectively. Because the exciting stick existed between the load cell and Plate 1, the influence of the additional mass on the natural frequency could not be avoided. Therefore, the peak frequency shifted to the lower-frequency region if the stick became long. To convert vibration energy into usable electric energy via the piezoelectric element, a suitable resistor that can efficiently consume the electric energy should be chosen. Figure 5 shows the experimental v₁ as a function of the resistance R_c. Because it can be ensured that v₁ is saturated with increasing R_c from approximately 100 kΩ, varying rapidly in the initial range of R_c, the resistance of 97.5 kΩ is valid.

Figure 6 shows the theoretical v₁ as a function of nondimensional excitation position r₁/r_c. Here, v₁ changes with r₁/r_c and it reaches the maximum value at approximately r₁/r_c = 0.45. Because it is natural that v₁ depends strongly on the vibration characteristics of Plate 1, the acceleration a₁ at the excitation position is also indicated in the same figure. Further, a₁ is maximized around r₁/r_c = 0.35, changing with r₁/r_c as with changes in v₁. Although it is remarkable that v₁ and a₁ are not identical in the excitation position, it is more significant that r₁/r_c = 0.4 is valid.

Because it was difficult to apply the additional mass to this theoretical procedure, a theoretical analysis was attempted by shifting the natural frequency of Plate 1, which was caused by changing R_n. Figure 7 shows the theoretical v₁ and a₁ as functions of R_n. R_n ranged from 1.222 to 137.4, and its variation corresponded to f = 200 − 320 Hz. Further, v₁ was maximized at approximately R_n = 1.7 and decreased with increasing R_n beyond the maximum value. Moreover, a₁ behaved with a tendency similar to v₁, whereas the maximum value appeared in the larger range of R_n in comparison with v₁. The theoretical and experimental situations in this study can be understood from these results.

Table 1. Mechanical and electrical properties of plate and piezoelectric element.

Figure 4. Voltage with electricity generation as function of excitation frequency.

Figure 5. Variations in voltage with resistance of resister to consume electric power.

Figure 6. Voltage and acceleration as function of excitation position.

Figure 7. Voltage and acceleration as function of rotational spring stiffness.

4.2. Electricity Generation Derived from Plate Vibration

Here, the power P_m supplied from the vibrator was calculated from the product between F and w_c1. Figure 8 shows the theoretical P_m as a function of the plate thickness h_c, which ranged from 1.5 to 4.5 mm. P_m decreased gradually with increasing h_c and was proportional to the square of w_c1, because w_c1 is proportional to F. However, the electric power P_e at the electricity generation is also exhibited in the same figure. Further, P_e had behavior similar to P_m, because v₁ had strong correlation to w_c1. Because the piezoelectric element was assumed to be incorporated in the electrical circuit of the energy-harvesting device and to be connected in series with the resistance for power consumption, it is natural that an electrical current was in-phase to the voltage. Therefore, P_e was also proportional to the square of v₁ and could be obtained from only the voltage because of Ohm’s law.

A close relationship between P_e and P_m was confirmed from these results. In addition, to consider this relationship specifically, the electricity generation efficiency P_em was defined as follows:

$P_{em}=\frac{P_e}{P_m}\times 100\left[\%\right].$ (27)

Figure 9 shows P_em derived from the above P_e and P_m as a function of h_c, so not only the theoretical but also the experimental P_em is indicated. In the case of only Plate 1, the theoretical P_em increased gradually with increasing h_c, whereas the experimental P_em presented a totally reverse tendency, where it decreased gradually with increasing h_c. In this manner, it is recognized that the discrepancy between the theoretical and experimental data expanded with increasing h_c.

In the analytical model of only Plate 1, the medium contacted on Plate 1 was not assumed (i.e., there is Plate 1 in vacuo). Therefore, the radiated sound field was not formed by the vibration of Plate 1, and the acoustic radiation power was almost spent in the electricity generation, so it is supposed that the above discrepancy took place, because the vibration of Plate 1 formed the sound field. As mentioned in Section 2.4, the radiation impedance Z_r consisted of the radiation resistance R_r of its real part and the radiation reactance X_r of its imaginary part. With respect to R_r, because the sound pressure P_s and the vibration velocity U₀e^jωt were in phase, R_r contributed the acoustic radiation of Plate 1. However, because P_s and U₀e^jωt that relate to X_r had a phase shift of 90˚, X_r did not take part in the acoustic radiation, whereas it functioned in Plate 1 as additional mass. Figure 10 shows variations in the radiation resistance and reactance with the plate thickness h_c; however, the normalized R_rn and X_rn were adopted as a substitute for R_r and X_r. They increased with h_c, with the result that the rate of vibration energy that was directly spent on the acoustic radiation increased with h_c. Then, because the additional mass meant that the surrounding medium was involved in the plate vibration, the vibration energy was consumed further with increasing h_c. Therefore, the discrepancy between the theoretical and experimental P_em in Figure 9 was caused by the acoustic radiation and additional mass, and expanded with increasing h_c because of the behaviors of the radiation resistance and reactance.

To estimate the effect of Z_r on the electricity generation characteristics, an analysis that involved the reactions F_ra and F_rb derived from Z_r was carried out using Equation (26). Here, F_ra and F_rb were in an out-of-phase state, not having a phase shift, so that they were mutually canceled and did not contribute to the electricity generation characteristics. Hence, the phase shift from being out of phase is denoted by Δα, and Figure 11 shows theoretical P_em as functions of Δα with changing h_c. Although P_em suddenly varied in the initial range of Δα, it converged on a constant value beyond the initial range. Then, the tendency shifted to the lager range of Δα with increasing h_c. Because the appropriate Δα could not be decided in this analysis, the theoretical P_em was estimated from Δα, which was measured by the acoustic experiment based on Figure 3, and it is also plotted by each circle in this figure. Further, Δα increased with h_c, with the result that P_em decreased rapidly with increasing h_c from 2.0 mm and converged in a greater range than 2.5 mm. These data are also reflected in Figure 9, whereas they are significantly less than the experimental data. This is because the circular piston vibration is assumed as the acoustic radiation source, and the effect of the reactions is overestimated. However, the theoretical and experimental results are similar and verified that the radiation impedance affects the electricity generation characteristics considerably.

4.3. Electricity Generation Using Mechanical-Acoustic Coupling

According to the results in the previous section, the application of the radiation power is a useful way to improve electricity generation characteristics. The improvement was attempted by using mechanical-acoustic coupling, which was brought to this electricity generation system by adding the cylinder and Plate 2, as shown in Figure 1 and Figure 2. The thicknesses of Plates 1 and 2 were the same, and the point force was set to 1 N, as with that of only Plate 1. Figure 12 shows the sound pressure levels L_pv, L_p1, and L_p2 as functions of the cylinder length L. The theoretical level L_pv was averaged over the entire volume of the cavity and was maximized at a specific L. This was when the plate thickness h_c and the excitation frequency f were set to 3 mm and 280 Hz, respectively, and the phase α₂ of the vibration of Plate 2 ranged from 0˚ to 180˚. The theoretical level L_pv peaked at 610 mm. The peaks were caused by the promotion of mechanical-acoustic coupling between the plate vibration and acoustic mode. Then, the acoustic modes were the (0, 0, 1) mode, whose plane modal shape is similar to that of the plate vibration mode (0, 0). The experimental levels L_p1 and L_p2, measured near Plates 1 and 2, corresponded to L_pv in the occurrence of those peaks, so that it obviously promoted coupling at approximately the above length.

The electric power P_e and the supplied power P_m with coupling were the results under such a situation involving the (0, 0, 1) mode. Although the electricity generation efficiency P_em was obtained from these powers, P_e was the total electric power generated by both plate vibrations. Figure 13 shows the theoretical and experimental P_em as functions of h_c, and P_em without coupling (i.e., by means of only the plate vibration), and is also indicated to estimate the effect of coupling. The theoretical P_em increased gradually with increasing h_c, and was very close to that of only the plate vibration without coupling. The experimental P_em was somewhat less than the theoretical result, whereas it tended to vary similarly

Figure 8. Electric and mechanical powers as function of plate thickness.

Figure 9. Variations in theoretical and experimental electricity generation efficiencies with plate thickness.

Figure 10. Radiation resistance and reactance as function of plate thickness.

Figure 11. Relationships between electricity generation efficiency and phase difference of radiated sound field when changing plate thickness.

Figure 12. Sound pressure level inside cavity as function of cylinder length.

Figure 13. Effect of mechanical-acoustic coupling on electricity generation efficiency.

to theoretical result and the difference from the theoretical result was reduced in comparison with that of only the plate vibration without coupling. This is because the vibration of Plate 1 contributed to the formation of the internal sound field and the vibration of Plate 2, via mechanical-acoustic coupling. Moreover, the expansion between the experimental values with increasing h_c demonstrates the validity of the application of mechanical-acoustic coupling to an electricity generation system with piezoelectric elements.

5. Conclusions

In this study, an electricity generation system, which consisted of a circular plate with a piezoelectric element installed at its center, was examined. To improve the electricity generation characteristics by using the acoustic radiation power derived from the plate vibration, a cylinder that had the above plates at both ends was adopted, and the mechanical-acoustic coupling between the plate vibrations and internal sound field was used. Then, the effect of mechanical-acoustic coupling on energy harvesting was estimated theoretically and experimentally from the electricity generation efficiency.

In the theoretical consideration, the electricity generation efficiency without coupling (i.e., by means of only the plate vibration) increased with the plate thickness. However, the efficiency showed the opposite tendency by means of adopting the radiation impedance in the analysis. This is because the phase differences between the reactions, which were derived from the respective impedances of both plate faces, expanded, and the influence of the reactions intensified with increasing plate thickness. This tendency was also demonstrated by the experiment. The theoretical and experimental efficiencies with coupling (i.e., by means of the cylinder having both end plates), also increased with the plate thickness. However, the reactions were not assumed on the outside surfaces of both plates in the analysis, and the experimental efficiency was somewhat less than the theoretical one. Therefore, it is obvious that the use of the acoustic radiation power via mechanical-acoustic coupling is useful for this electricity generation system.

The excitation in the natural frequency is a rare case and when it is derived from not only random vibration but also vibrations of multi peaks, this electricity generation system does not work even if its characteristics have been improved by coupling. In order to actually use this system, the system should be devised to deal with such excitations together with making further refinements to the electricity generation efficiency.

Acknowledgements

This work was partially supported by JSPS KAKENHI Grant Number 15K05874.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Anton, S.R. and Sodano, H.A. (2007) A Review of Power Harvesting Using Piezoelectric Materials (2003-2006). Materials and Structures, 16, 1-21. https://doi.org/10.1088/0964-1726/16/3/R01
[2]	Ali, W.G. and Ibrahim, S.W. (2012) Power Analysis for Piezoelectric Energy Harvester. Energy and Power Engineering, 4, 496-505. https://doi.org/10.4236/epe.2012.46063
[3]	Basari, A.A., Awaji, S., Wang, S., Hashimoto, S., Kumagai, S., Suto, K., Okada, H., Okuno, H., Homma, B., Jiang, W. and Wang, S. (2014) Shape Effect of Piezoelectric Energy Harvester on Vibration Power Generation. Journal of Power and Energy Engineering, 2, 117-124. https://doi.org/10.4236/jpee.2014.29017
[4]	Yamada, K., Matsuhira, H. and Utsuno, H. (2014) Improvement of Efficiency of Piezoelectric Element Attached to Beam Based on Mechanical Impedance Matching. Journal of Sound and Vibration, 333, 52-79. https://doi.org/10.1016/j.jsv.2013.08.038
[5]	Piñeirua, M., Doaré, O. and Michelin, S. (2015) Influence and Optimization of the Electro Deposition in a Piezoelectric Energy Harvesting Flag. Journal of Sound and Vibration, 346, 200-215. https://doi.org/10.1016/j.jsv.2015.01.010
[6]	Tsaplev, V., Konovalov, R. and Abbakumov, K. (2015) Disk Bimorph-Type Piezoelectric Energy Harvester. Journal of Power and Energy Engineering, 3, 63-68. https://doi.org/10.4236/jpee.2015.34010
[7]	Larbi, W., Deü, J.F. and Ohayon, R. (2012) Finite Element Formulation of Smart Piezoelectric Composite Plates Coupled with Acoustic Fluid. Composite Structures, 94, 501-509. https://doi.org/10.1016/j.compstruct.2011.08.010
[8]	Larbi, W., Deü, J.F. and Ohayon, R. (2014) Coupled FEM/BEM for Control of Noise Radiation and Sound Transmission Using Piezoelectric Shunt Damping. Applied Acoustics, 86, 146-153. https://doi.org/10.1016/j.apacoust.2014.02.003
[9]	Tsuchiya, H., Moriyama, H. and Iwamori, S. (2016) Electricity Generation Characteristics of Energy-Harvesting System with Piezoelectric Element Using Mechanical-Acoustic Coupling. Advances in Acoustics and Vibration, 2016, 1-11. https://doi.org/10.1155/2016/4217517