The Equilibrium of Fractional Derivative and Second Derivative: The Mechanics of a Power-Law Visco-Elastic Solid ()
1. Introduction
The equilibrium of time derivatives of the function of x is denoted as
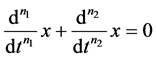 i.e.
i.e.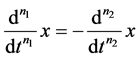 (1)
(1)
where d is the differential operator; and n1 and n2 are the orders of differentiation, where n1 ≠ n2, and n1 and n2 are not necessarily integers. These kinds of differential equations are common in dynamics, e.g. in a mass-spring system, where the spring force (0th derivative) is in equilibrium with the inertial force (2nd derivative).
The term equilibrium should not be confused with the term equality of derivatives, such as
 i.e.
i.e. (2).
(2).
The latter equalities define the so-called cyclodifferential functions [1] , i.e. functions being preserved on repeated differentiations, which are for example:
1) if 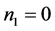 and
and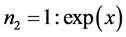 ;
;
2) if 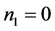 and
and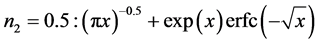 ;
;
3) if  and
and ,
, 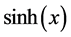 , and
, and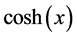 ;
;
4) if  and
and ;
;
5) if  and
and 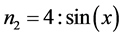 and
and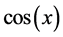 .
.
The aforementioned equilibrium, however, yields solutions different from the traditional cyclodifferential functions:
1) if 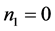 and
and![]() ; e.g.
; e.g.![]() ;
;
2) if ![]() and
and![]() ,
,![]() ;
;
3) if ![]() and
and![]() ;
;
It is therefore of interest to investigate other equilibria involving fractional derivatives, e.g. with orders of n1 = 0.5 and n2 = 2, or, in general, 0 < n1 < 1 and n2 = 2.
These kinds of (extraordinary) differential equations characterize the behaviour of power-law visco-elastic solids. The constitutive equation of a power-law visco-elastic solid, derived from stress relaxation, is
![]() (3)
(3)
[2] [3] , where ![]() is the transformed force,
is the transformed force, ![]() is the transformed deflection of solid’s centre of mass (COM), s is the complex variable of a Laplace-transformed function, k is the stiffness (dF/dx), η is the viscosity constant, and Γ denotes a Gamma function. Considering that kΓ(1 − η) are merely constants, Equation (1) reveals that the function of the force F is a fractional derivative of the deflection x, specifically the ηth derivative. Furthermore, from Equation (1), 0 ≤ η < 1, as the Gamma function of Equation (1) approaches infinity when η approaches 1.
is the transformed deflection of solid’s centre of mass (COM), s is the complex variable of a Laplace-transformed function, k is the stiffness (dF/dx), η is the viscosity constant, and Γ denotes a Gamma function. Considering that kΓ(1 − η) are merely constants, Equation (1) reveals that the function of the force F is a fractional derivative of the deflection x, specifically the ηth derivative. Furthermore, from Equation (1), 0 ≤ η < 1, as the Gamma function of Equation (1) approaches infinity when η approaches 1.
Substituting the function ![]() for a constant deflection x0 applied via a Heaviside function, i.e. for x0/s, with subsequent rearranging and taking the inverse Laplace transform, results in the standard stress relaxation function of a power-law visco-elastic solid, namely F = x0kt−η.
for a constant deflection x0 applied via a Heaviside function, i.e. for x0/s, with subsequent rearranging and taking the inverse Laplace transform, results in the standard stress relaxation function of a power-law visco-elastic solid, namely F = x0kt−η.
Equation (1) corresponds to Scott Blair’s [4] spring pot [5] , a rheological element being “intermediate” between a Hookean spring and a Newtonian damper. However, the structure of the constitutive Equation (1) depends on which time-dependent phenomenon it is derived from. Equation (3) was derived from a power decay stress relaxation, F = x0kt−η; the corresponding power creep resulting from Equation (3) is not x = F0tη/k, but rather x = F0tηsinc(ηπ)/k.
In horizontal oscillations or impact, i.e. without gravitational force, two forces are in equilibrium: the inertial force and the applied or impact force at the contact between free-body diagram and the environment (Figure 1). As the inertial force equals the 2nd time derivative of x, i.e. the acceleration, multiplied by the mass m, i.e. m d2x/dt2, and the applied or impact force equals the ηth time derivative of x, multiplied by kΓ(1 − η) according to Equation (3), the equation of horizontal oscillations or impact exhibits the equilibrium of fractional time derivative of x and second time derivative of x. The multipliers m and kΓ(1 − η), are omitted subsequently, unless they are necessary for understanding, so that these constants do not have to be repeated at each single instance.
The aim of this paper is to analyse this equilibrium and to evaluate the properties of deflection; velocity; and forces, as well their relationship to fractal derivatives.
2. Mathematical Analysis
The force equilibrium of horizontal oscillations or impact is defined as:
![]() (4)
(4)
[2] where the term on the left side of the addition sign equals the transformed inertial force, i.e. the inverse Laplace transform of acceleration times mass (md2x/dt2), and the term on the right side of the addition sign equals the applied or impact force according to Equation (3); and where v0 denotes the initial velocity. Note that the initial deflection, x0, is zero. As v0 is greater than 0, the rules for transforming derivatives result in the term “−v0m”. The latter reflects a unit impulse of x (in the Laplace space) that increases the initial velocity from 0 to v0 instantaneously by a unit step (Heaviside) function, the integral of the unit impulse.
![]()
Figure 1. Rheological model (left) and power-law visco-elastic solid (right); ![]() : centre of mass COM, 1: point mass, 2: symbol of ‘spring pot’ [5] , 3: visco-elastic solid; x: displacement, v: velocity, a: acceleration, FI: inertial force (decelerated COM), FA: applied force (contact force, impact force).
: centre of mass COM, 1: point mass, 2: symbol of ‘spring pot’ [5] , 3: visco-elastic solid; x: displacement, v: velocity, a: acceleration, FI: inertial force (decelerated COM), FA: applied force (contact force, impact force).
Solving for ![]() and multiplying by m/m yields
and multiplying by m/m yields
![]() . (5)
. (5)
Let
![]() (6)
(6)
then
![]() . (7)
. (7)
Substituting Equation (7) for ![]() in Equation (1) yields the applied or impact force function
in Equation (1) yields the applied or impact force function
![]() . (8)
. (8)
Equation (8) is the fractional (ηth) derivative of Equation (5) times kΓ(1 − η).
The first derivative of Equation (7) yields the velocity of the solid’s COM, whose x0 is zero
![]() (9)
(9)
The second derivative of Equation (7) yields the acceleration of the solid’s COM, which, times m, corresponds to the inertial force acting on the COM
![]() (10)
(10)
and
![]() . (11)
. (11)
If η = 0, then the equation of horizontal oscillation or impact becomes the equilibrium of the function of x (times k) and its second derivative (times m):
![]() . (12)
. (12)
The analytical solution after applying the inverse Laplace transform equals the constitutive equation of undamped oscillation, i.e. the behaviour of a Hookean spring:
![]() . (13)
. (13)
If η = 1, then the equation of horizontal oscillations or impact becomes the equilibrium of first derivative of x and second derivative of x:
![]() (14)
(14)
the analytical solution of which is the integral of e−Ct plus an integration constant for satisfying the initial condition of x0 = 0:
![]() . (15)
. (15)
Considering that C → ∞ (i.e. Γ0) when η → 1, Equation (15) reduces to x = 0, i.e. the behaviour of an incompressible, iso-volumetric fluid, and therefore of a Newtonian damper. Consequently, for the equation of a horizontal oscillation or impact, 0 ≤ η ≤ 1, as there is a solution for η = 1. Furthermore, Equation (4), the force equilibrium of horizontal oscillations or impact, reflects the principle of Scott Blair’s rheological element [4] , a material being “intermediate” between a Hookean spring and a Newtonian damper.
If η = 0.5, then the equation of horizontal oscillation or impact becomes the equilibrium of semi-derivative and second derivative of x:
![]() . (16)
. (16)
Analytical solutions of Equation (16) and the more generalized Equation (7) are found when using the Mittag-Leffler Equation. Having different powers of s in the denominator of the transformed equations, e.g. 2 and 0.5 in Equation (16), and 2 and η in Equation (7), leads to Equation (17) with generalized powers of s, namely α and β,
![]() , (17)
, (17)
the inverse Laplace transform of which is
![]() (18)
(18)
[6] , where Eα,β denotes a generalized Mittag-Leffler function. Modifying Equation (17) to the structure of Equation (7) yields
![]() (19)
(19)
so that β = 2, β − α = η, α = 2 − η. Note that α equals the difference between the two orders of differentiation, n1 and n2 of Equation (1), i.e. the 2nd and the fractional (ηth) derivatives. Note that C is negative for solving Equation (1), i.e. the equilibrium case, whereas C would be positive for solving Equation (2), the equality case. As a result, the analytical solution of Equation (7), considering Equation (18), is
![]() . (20)
. (20)
Validating Equation (20) for η = 0 and η = 1, with C = 1 and v0 = 1, yields
![]()
and
![]() (21)
(21)
thereby mirroring the functions of Equations (13) and (15). The derivatives of Equation (20) are
![]() (22)
(22)
![]() (23)
(23)
![]() (24)
(24)
![]() (25)
(25)
where a is the acceleration, FI is the inertial force, and FA is the applied force (Figure 1), respectively. In the course of multiple and fractal differentiations, α remains constant, whereas β reduces by the order of derivative.
3. Oscillation and Impact Model
Oscillations and impact were modeled in horizontal direction, to avoid any influence by the gravitational force. For evaluating the damping and impact dynamics, the solid was represented by a point mass (the solid’s centre of mass, COM) tethered to the frame by a power-law visco-elastic spring (Figure 1). Thus, the model allowed for evaluating both compressive and tensile forces acting on the solid. The point mass was subjected to an initial velocity v0. Equations (7) and (8)-(11) were solved numerically for viscosity constants η from 0 to 1 (k, m, and v0 were set to unity) by using the INVLAP function in Matlab2014b (by Math Works, Natick MA, USA), based on the algorithm of [7] , and by using the Mittag-Leffler function (MittagLefflerE) in Mathematica10 (by Wolfram, Champaign IL, USA). The accuracy of the algorithms was validated by the equilibrium of inertial and applied (impact) force, i.e. by Equations (4), (8) and (11)
![]() (26)
(26)
i.e. the equilibrium of ηth derivative of x and second derivative of x.
4. Terminology
The term oscillation is used for simple harmonic oscillation, undamped or underdamped, whereby the centre of mass (COM) oscillates about, and therefore crosses, the zero line, i.e. x0, the COM position of the unloaded solid.
The term reciprocation is used for forward-backward motion of the horizontally moving COM without crossing the zero line; this term is used exclusively for the transition from underdamped to overdamped states (to be explained in detail below); note that this transition is not related to critical damping.
The magnitude and direction of displacement, velocity, and acceleration of the COM; and of the inertial and impact force are defined as follows:
Displacement x and velocity v are positive on compression, and negative on expansion and tension.
The fractal derivative of the displacement is initially positive. The applied or impact force FA results from the fractal derivative, if multiplied by kΓ(1 − η) and by −1. Therefore, the applied or impact force is initially negative, which corresponds to compression. Tension causes a positive applied force.
The 2nd derivative of the displacement, the acceleration a, is initially negative. The inertial FI force results from the 2nd derivative, if multiplied by m and by −1. Therefore, the inertial force is initially positive.
5. Results
In this section, the displacement, velocity and forces acting on a visco-elastic solid of η = 0.5 are explained first, as the applied or impact force corresponds to the semi-derivative of the displacement. Subsequently, the viscosity is expanded to 0 ≤ η ≤ 1 to understand the effect of different viscosities on the behaviour of the solid at impact. Finally, the damping behaviour and the coefficient of restitution COR are explained as a function of η.
5.1. Impact of a Solid with Viscosity η = 0.5, the Equilibrium of Semi-Derivative and 2nd Derivative
According to Equation (16), the applied or impact force, i.e. the semi-derivative of x, multiplied by kΓ(1 − η), is in equilibrium with the inertial force, i.e. the second derivative of x(multiplied by m). The solution of this EODE (extraordinary differential equation), shown in Figure 2, exhibits an overdamped movement of the COM that, after maximal deflection, returns to the initial position after some minor fluctuations. The semi-derivative of this function (times kΓ(1 − η)), i.e. the applied or impact force, is a
![]()
Figure 2. Displacement function of the COM (centre of mass) of a visco-elastic solid and its derivatives against time; the viscosity η of the solid is 0.5; k is the stiffness, η is the viscosity constant, and Γ denotes a Gamma function; the semiderivative times kΓ(1 − η) corresponds to the applied force or impact force (after multiplying by −1); the 1st derivative corresponds to the velocity of the COM; the 2nd derivative times the mass m corresponds to the inertial force (after multiplying by −1); k, v0 (initial velocity), and m are unity.
mirror image of the 2nd derivative (times the mass, which is unity here), i.e. the inertial force.
Considering the two extreme cases, namely undamped oscillation if η = 0, according to Equation (13), and maximal damping (no movement, x = 0) if η = 1, according to Equation (15), it is evident that η = 0.5 yields a damped function.
After the initial positive semi-derivative spike, the signal becomes negative at t = 2.017 s (Figure 2), corresponding to a positive applied force (or impact force). This positive force indicates that the solid is under tension, but the deflection of the COM, x, is still positive (compressed solid). Although the solid is still compressed at t = 2.017 s, it has already fully relaxed due to dissipation of elastic energy through inner viscous friction, and the viscosity of the solid opposes its expansion. Thus, the applied force is tensile.
5.2. Expansion to 0 ≤ η ≤ 1
Figure 3 shows the displacement functions of viscosities η ranging from 0 to 1. The functions are characterised by various degrees of underdamping and overdamping. In addition to that, the frequency of the underdamped functions changes to slightly smaller wavelengths as the time progresses. The displacement functions terminate in a power decay which is a reverse creep effect. Reverse creep decay occurs at a power of η − 1 (negative gradient). While viscous creep is a result of loading a material with a constant force or stress, reverse creep happens if the load drops to zero, and the compressed material expands and returns to the original shape, i.e. to x0.
Figure 4 and Figure 5 show the first derivatives of the displacement functions (velocity) and the fractional derivatives (applied force, impact force). The velocity functions exhibit a power decay at a power of 2 − η. (positive gradient). The velocity is negative
![]()
Figure 3. Displacement functions of the COM (centre of mass) of a viscoelastic solid against time, for viscosities η of 0 − 1;k, v0 (initial velocity), and m are unity.
![]()
Figure 4. Velocity functions of the COM (centre of mass) of a viscoelastic solid against time, for viscosities η of 0 - 1; k, v0 (initial velocity), and m are unity.
![]()
Figure 5. Force functions of the COM (centre of mass) of a viscoelastic solid against time, for viscosities η of 0 - 1; k, v0 (initial velocity), and m are unity.
when decaying, as the material returns to its original shape. The fractional derivative functions decay at a power of 3 − η; the fractional derivative is negative when decaying, which corresponds to a positive applied force (tensile force), a negative inertial force, a positive acceleration and a negative deceleration. This means that the COM moves away from the frame and is decelerated when decaying.
Figure 6 and Figure 7 show the contour plot and 3D graph of the displacement function against viscosity η and time. At lower viscosities, the oscillations of the COM displacement are clearly visible, fading out at higher viscosities.
Figure 8 shows the 3D graph of the acceleration function (2nd derivative; inertial force) against viscosity and time. As the viscosity increases, the initial acceleration and force spikes become excessively high, whereas the data approach zero subsequently.
5.3. Damping
As already mentioned above, the displacement data show oscillations (underdamping) initially (at least at smaller viscosities), and terminate in a power decay (overdamping). This behaviour stands in sharp contrast to standard damping of a mass-spring-damper system (point mass in series with a Voigt model, i.e. a linear spring and a linear damper in parallel). In the latter model, damping depends on the damping ratio ζ, which defines under-, critical and over-damping, if the damping ratio is ζ < 1, ζ = 1 or ζ > 1, respectively. As ζ approaches 1, the amplitude of the underdamped oscillations asymptotes to zero and their wavelengths increase, until the oscillations vanish in an exponential
![]()
Figure 6. Contour plot of the displacement function of the COM (centre of mass) against time (in seconds) and viscosity; k, v0 (initial velocity), and m are unity; the displacement is colour-coded.
![]()
Figure 7. 3D plot of the displacement function (normalized) of the COM (centre of mass) against time (in seconds) and viscosity; the figure is posterized for contour enhancement; k, v0 (initial velocity), and m are unity.
decay at ζ = 1 (critical damping, transition from under- to overdamping). Under- and over-damping of a Voigt model are exclusively disjunctive, i.e. a system is either overdamped or underdamped throughout its time history.
In a power-law visco-elastic solid, however,
1) the wavelengths of underdamped oscillations decrease as the viscosity increases;
2) under- and overdamping are not exclusively disjunctive but (co-)exist consecutively throughout the time history of the COM displacement function (underdamping at smaller times and overdamping at larger times); and
3) there is no critical damping but rather a transition phase from under- to overdamping, whereby this transition is characterised by a reciprocating COM.
The three damping phases, underdamping, transition, and overdamping are a function of time and occur consecutively after the initial displacement of the COM. At the initial deflection of an oscillating COM, or at impact, the COM approaches the frame
![]()
Figure 8. 3D plot of the inertial force function (normalized) of the COM (centre of mass) against time (in seconds) and viscosity; k, v0 (initial velocity), and m are unity.
and reaches its maximal displacement. After this displacement peak A (Figure 9(a)), damping sets in. The three damping phases are defined as follows:
1) Underdamping: after the initial displacement peak A, the COM oscillates about the zero line (x0), until it crosses the zero line the last time and reaches a positive peak B (Figure 9(a)).
2) Transition phase: after this positive peak B, the COM displacement values stay positive, and reciprocate slightly, with positive and negative gradients, until they reach a peak C (Figure 9(a)) after the last positive gradient. The transition phase can already start at peak A if underdamping phased out at higher viscosities (at η = 0.40088 in Figure 9(b)).
3) Overdamping: after peak C, the COM displacement decays (negative gradient) to zero (i.e. x0), by asymptoting towards a power decay of a power of η − 1 (negative power, as the gradient of the decay is negative). The overdamping phase can already start at peak A if both underdamping and transition phased out at higher viscosities (at η = 0.57774 in Figure 9(b)).
This constitutes a new definition of damping, where under- and over-damping do not only depend on the degree of viscosity but also depend on the time, thereby existing consecutively as a function of time. Figure 9 exemplifies the three phases at η = 0.37 (Figure 9(a)), as well as the damping phase diagram against η and time (Figure 9(b)).
![]() (a)
(a)![]() (b)
(b)
Figure 9. (a) (top): displacement function (red) of the COM of a visco-elastic solid of viscosity η = 0.37; A, B, C = peaks that define the boundaries between underdamping, transition and overdamping; blue curve: power decay function of the overdamping phase which the displacement function asymptotes to; (b) (bottom): damping phase diagram against viscosity and time; the dashed line corresponds to the viscosity η = 0.37 of the top diagram; k, v0 (initial velocity), and m are unity.
5.4. Coefficient of Restitution COR
The COR is the ratio of output velocity of the COM to initial (input) velocity. For impacts, these velocities are rebound and incident velocity, respectively. In a damped oscillating COM, the output velocity corresponds to the first negative velocity peak (Figure 10(a)). The higher the viscosity, the lower is the COR. As viscosity causes energy loss through internal friction, the relative energy lost corresponds to 1 − COR2. Figure 10(b) shows the COR data against the viscosity η. At η of 0, 0.5, and 1, the COR is 1, 0.3002, and 0, respectively. At η = 0.5, the energy loss is 91%.
6. Discussion
Comparable behaviour of damping, i.e. co-existence of under- and overdamping was described by Burov and Barkai [8] [9] in fractional Langevin equations. The authors describe three damping solutions:
1) an underdamped solution as the displacement of a particle oscillates with a non-monotonic decay and crosses the zero line;
2) a non-monotonic decay solution without zero crossing; and
3) an overdamped solution as monotonically decaying, where the decay is of the power law type.
They define a “critical exponent”, where the exponent corresponds to the fractional order of the displacement’s derivative. This exponent corresponds to the viscosity η in Equation (2) and ranges between 0 and 1. If the exponent is smaller than the “critical”
![]()
![]() (a) (b)
(a) (b)
Figure 10. (a) (left): output velocity of four different viscosities (input velocity = 1); k, v0 (initial velocity), and m are unity; (b) (right): COR against viscosity.
one, then “the overdamped behavior totally disappears, and the decay to equilibrium is never monotonic” [8] . In the underdamped regime, for large times, the displacement is greater than 0 [9] , and yet allegedly, “solutions with monotonic decay are not found”. This stands in sharp contrast to own displacement results, which always terminate in overdamping with a power decay, independent of the magnitude of η. Unsurprisingly, the “critical exponent” of Burov and Barkai [8] [9] , 0.402 ± 0.002, is identical to the viscosity that marks the border between underdamping and transition phase (Figure 9(b)), namely η = 0.40088. Other critical exponents were found [9] if the system is driven by an external oscillator (forced oscillations) instead of oscillating freely. In the results of the present study, however, another exponent was found, that marks the border between transition phase and overdamping (Figure 9(b)) of free oscillations, namely η = 0.57774. In the present study (Figure 9), considering that the three phases exist consecutively throughout the time history of damping, the three “solutions” of Burov and Barkai [8] [9] are:
1) underdamping, followed by the transition phase, followed by overdamping (Figure 9(a) and Figure 9(b)) for 0 < η < 0.40088;
2) transition phase, followed by overdamping (Figure 9(b)) for 0.40088 < η < 0.57774; and
3) overdamping only (Figure 9(b)), for 0.57774 < η < 0;
with special cases of η = 0 (undamped) and η = 1 (maximally damped, rigid). In addition to that, a method was presented in the present study (Figure 9(a) and Figure 9(b)) for identifying the borders between the three phases.
Sandev et al. [10] observed changing damping behaviours, similar to the “solutions” of [8] [9] , depending on the magnitude of coefficients of a generalised fractional Langevin equation.
7. Conclusions
The equilibrium of fractional derivative and 2nd derivative of a function implies that this function is a damped oscillation function. If the viscosities of a power-law visco-elastic solid are 0 or 1, then the deflection function is either undamped or maximally damped, respectively. Viscosities η between 0 and 1 result in under- and overdamping. In contrast to a mass-spring-damper system (point mass in series with a Voigt model, i.e. a linear spring and a linear damper in parallel), in which under- and overdamping are exclusively disjunctive, separated by critical damping, in a power-law visco-elastic model under- and overdamping exist consecutively as time progresses, separated by a transition phase. This analytical discovery constitutes a new definition of damping, related to non-linear visco-elastic solids, rather than to linear visco-elastic structures.
The innovation of this discovery is critical for designing non-linear visco-elastic power-law dampers and fine-tuning the ratio of under- and overdamping, considering that three phases―underdamping, transition, and overdamping―co-exist consecutively if η < 0.401; two phases―transition and overdamping―co-exist consecutively if 0.401 < η < 0.578; and one phase―overdamping―exists exclusively if η > 0.578.
Acknowledgements
The author thanks the anonymous reviewers of this paper for their insightful and valuable comments and suggestions on the manuscript, which have led to significant improvements of the paper.