Subject Areas: Applied Physics
1. Introduction
The quantum theory (cf. [1] - [5] ) gives accurate and at-times-remarkably accurate numerical predictions. Much experimental data has fit to quantum predictions for long time.
As for the foundations of the quantum theory, Leggett-type non-local variables theory [6] is experimentally investigated [7] - [9] . The experiments report that the quantum theory does not accept Leggett-type non-local variables interpretation.
As for the applications of the quantum theory, the implementation of a quantum algorithm to solve Deutsch’s problem [10] on a nuclear magnetic resonance quantum computer was reported firstly [11] . An implementation of the Deutsch-Jozsa algorithm on an ion-trap quantum computer is also reported [12] . There are several attempts to use single-photon two-qubit states for quantum computing. Oliveira et al. implemented Deutsch’s algorithm with polarization and transverse spatial modes of the electromagnetic field as qubits [13] . Single- photon Bell states are prepared and measured [14] . Also the decoherence-free implementation of Deutsch’s algorithm was reported by using such single-photon and by using two logical qubits [15] . More recently, a one- way based experimental implementation of Deutsch’s algorithm was reported [16] .
In quantum mechanics, the uncertainty principle is any of the variety of mathematical inequalities asserting a fundamental limit to the precision with which certain pairs of physical properties of a particle known as complementary variables, such as its position x and momentum p, can be known simultaneously. For instance, in 1927, Werner Heisenberg stated that the more precisely the position of some particle is determined, the less precisely its momentum can be known, and vice versa [17] . The formal inequality relating the standard deviation of position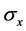 
and the standard deviation of momentum 
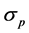was derived by Earle Hesse Kennard [18] later that year and by Hermann Weyl [19] in 1928.
Recently, Ozawa discusses universally valid reformulation of the Heisenberg uncertainty principle on noise and disturbance in measurement [20] . And experimental demonstration of a universally valid error-disturbance uncertainty relation in spin-measurements is discussed [21] . Violation of Heisenberg’s error-disturbance uncer- tainty relation in neutron spin measurements is also discussed [22] .
In this paper, we derive the optimal limitation of Heisenberg’s uncertainty principle in a specific two-level system (e.g., electron spin, photon polarizations, and so on). Some physical situation is that we would measure 
and
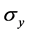, simultaneously. The optimality is certified by the Bloch sphere. We show that a violation of Heisenberg’s uncertainty principle means a violation of the Bloch sphere in the specific case. Especially, the Schrödinger uncertainty relation is equivalent to the Bloch sphere relation in the physical situation. Thus, the experiments [21] [22] show a violation of the Bloch sphere when we use 
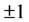as measurement outcome. This conclusion agrees with recent researches [23] [24] .
2. The Schrödinger Uncertainty Relation
In this section, we review the Schrödinger uncertainty relation. The derivation shown here incorporates and builds off of those shown in Robertson [25] , Schrödinger [26] and standard textbooks such as Griffiths [27] .
For any Hermitian operator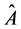
, based upon the definition of variance, we have
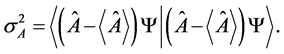(1)
We let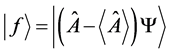 
and thus
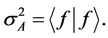(2)
Similarly, for any other Hermitian operator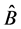 
in the same state
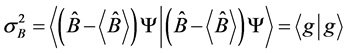(3)
for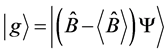
.
The product of the two deviations can thus be expressed as
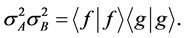(4)
In order to relate the two vectors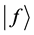 
and
, we use the Cauchy-Schwarz inequality [28] which is defined as
![]()
(5)
and thus Equation (4) can be written as
![]()
(6)
Since ![]()
is in general a complex number, we use the fact that the modulus squared of any complex number z is defined as![]()
, where ![]()
is the complex conjugate of z. The modulus squared can also be expressed as
![]()
(7)
We let ![]()
and ![]()
and substitute these into the equation above to get
![]()
(8)
The inner product ![]()
is written out explicitly as
![]()
(9)
and using the fact that ![]()
and ![]()
are Hermitian operators, we find
![]()
(10)
Similarly it can be shown that![]()
.
For a pair of operators ![]()
and![]()
, we may define their commutator as![]()
.
Thus we have
![]()
(11)
and
![]()
(12)
where we have introduced the anticommutator,![]()
.
We now substitute the above two equations above back into Equation (8) and get
![]()
(13)
Substituting the above into Equation (6) we get the Schrödinger uncertainty relation
![]()
(14)
3. Main Result
In this section, we present an example that the Schrödinger uncertainty relation is optimal. The optimality is certified by the Bloch sphere. In fact, a violation of the Schrödinger uncertainty relation means a violation of the Bloch sphere in the specific case. We derive the Schrödinger uncertainty relation by using the Bloch sphere
relation in the specific case. Let ![]()
be the variance of![]()
, i.e.,![]()
.
Statement 1
![]()
(15)
Proof. By using![]()
, we have
![]()
(16)
Thus,
![]()
(17)
QED
We define N as follows:
![]()
(18)
We define S as follows:
![]()
(19)
We discuss the relation between N and S in the following statement.
Statement 2
![]()
(20)
Proof. We have the following relation:
![]()
(21)
QED
Thus the Schrödinger uncertainty relation is optimal in the specific case. The optimality is certified by the Bloch sphere. A violation of the Schrödinger uncertainty relation means a violation of the Bloch sphere in the specific case. Thus, the experiments [21] [22] show a violation of the Bloch sphere when we use ![]()
as measurement outcome. This conclusion agrees with recent researches [23] [24] .
4. Conclusions
In conclusions, we have derived the optimal limitation of Heisenberg’s uncertainty principle in a specific two- level system (e.g., electron spin, photon polarizations, and so on). Some physical situation has been that we would measure ![]()
and![]()
, simultaneously. The optimality has been certified by the Bloch sphere. We have shown that a violation of Heisenberg’s uncertainty principle means a violation of the Bloch sphere in the specific case. Thus, the experiments [21] [22] have shown a violation of the Bloch sphere when we use ![]()
as measurement outcome. This conclusion has agreed with recent researches [23] [24] .
It is very interesting to study whether Heisenberg’s uncertainty principle would violate when we would use a new measurement theory ![]()
[24] as measurement outcome.