The Asymptotic Iteration Method for the Eigenenergies of the a Novel Hyperbolic Single Wave Potential ()
1. Introduction
The numerical solutions of the Schrödinger equation have taken a great deal of interest in the description of nuclear motion in molecules in the Born-Oppenheimer approximation or in the description of atoms and molecules in self-consistent field approximations. In most cases the use of numerical methods is necessary, where analytical solutions are not possible or difficult to find and the number of exactly solvable problems is very limited [1] . Over the past decade, several numerical methods have been developed for the solution of the Schrödinger equation, such as the Nikiforov-Uvarov (NU) method, Runge-Kutta methods, Matrix Diagonalization Method (MDM), Discrete Variable Method (DVM), Spectral Method [2] - [6] , and the asymptotic iteration method (A.I.M).
Ever since the inception of empirical Morse potential about 85 years ago, a vast number of potential functions have been reported for molecules, with varying degrees of flexibility and accuracy [7] . In this work we are interested to calculate the eigenvalues of hyperbolic single wave potential introduced by H. Bahlouli and A. D. Alhaidari [8] [9] some years ago. The new solvable hyperbolic single wave potential introduced given as
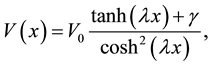(1)
where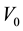 
and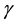 
are real potential parameters and 
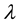is a length scale that determines the range of the potential. The first term of this potential is completely new and cannot be predicted by any of the classical approaches based on diagonal representations. However, the second part is a special case of the hyperbolic Pöschl-Teller potential that has an exact conventional (diagonal representation) solution. Physically, the most interesting situation is when the parameter 
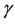lies between 
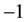and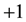 
in which case the shape of this potential becomes a hyperbolic single wave about the origin [8] [9] . The potential has two local extrema at
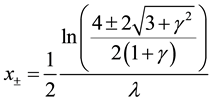(2)
They have dealt with the case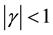 
which carries a richer structure for a given potential.
In [8] they have dealt with case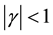 
which carries a richer structure for a given potential. The configuration of this potential allows for both resonances and bound states, which is contrary to the case ![]()
where either bound or resonance energy states are allowed. Nonetheless, their approach can still handle the case ![]()
as long as![]()
. In this work, we apply the asymptotic iteration method, in order to find eigenvalues of hyperbolic single wave potential.
This paper is divided into the following sections. In Section 2, we describe the asymptotic iteration method which introduced to find the solutions for the second-order differential equation. In Section 3, change of variables has been done which allows as transforming Schrödinger equation to another form in order to apply the method to solve the equation with hyperbolic single wave potential. In Section 4, our numerical calculation results have been presented for the eigenvalues of the hyperbolic single wave potential.
2. Solution Methodology
Recently a technique called the asymptotic iteration method (AIM) has been introduced [10] to obtain eigenvalues of second-order homogeneous differential equations. In the case of the Schrödinger equation the AIM was found to reproduce the energy spectrum exactly for most exactly solvable potentials [11] - [13] , while for non- exactly solvable potentials it produces very good results [14] - [18] .
The first step in applying this method to solve Schrödinger-type equations is to transform these equations, with the aid of appropriate asymptotic forms, to second-order homogeneous linear differential equations of the general form
![]()
(3)
where the primes of ![]()
denote derivatives with respect to x, ![]()
and ![]()
are functions in![]()
. The solution of (3) follows from the symmetric structure of the right-hand side of Equation (3). Therefore, if we differentiate (3) with respect to x, we get
![]()
(4)
where
![]()
(5)
By differentiating Equation (4), we get
![]()
(6)
for which
![]()
(7)
In general, the ![]()
and ![]()
derivatives of (3), ![]()
, are
![]()
(8)
Respectively, where
![]()
(9)
The ratio of the ![]()
and ![]()
derivatives can be expressed as
![]()
(10)
For sufficiently large j, we can introduce the “asymptotic” aspect of the method, that is, if
![]()
(11)
Thus, Equation (13) can be reduced to
![]()
(12)
Which yields
![]()
(13)
where ![]()
is the integration constant, and the right-hand side of Equation (13) follows from Equation (9) and the definition of![]()
. Substituting Equation (13) into Equation (8) we obtain a first-order differential equation
![]()
(14)
Which, in turn, yields the general solution to Equation (3)
![]()
(15)
3. Formulation of the Problem
The time-independent Schrödinger equation, in the field of potential ![]()
can be written as
![]()
(16)
where ![]()
is the hyperbolic single wave potential in Equation (1)
Substituting Equation (1) into Schrödinger equation (16) we obtain
![]()
(17)
Before applying AIM to this problem, we have to transform the modified Schrödinger equation (17) to an amenable form for AIM. By using the change of variables, we can simplify Equation (17) by eliminating the hyperbolic functions ![]()
and ![]()
as
![]()
(18)
After making the convenient change of variable, a straightforward calculation shows that Equation (17) becomes
![]()
(19)
With ![]()
and ![]()
are given by
![]()
(20)
and
![]()
(21)
AIM can be applied to the final form of the Schrödinger equation (19).
In order to calculate the eigenvalues![]()
, ![]()
we need to iterate the expansion
![]()
(22)
In each iteration, the expansion will depend on two variables E and r. The calculated eigenvalues ![]()
by the mean of the condition ![]()
should depend on the choice of r. Nevertheless, the choice of r is observed to be critical only to the speed of the convergence of the eigenvalues![]()
, as well as for the stability of the process. In our work, it is observed that the best starting value for r must be![]()
. Therefore, at the end of the iterations we put![]()
.
4. Results and Discussions
In this section, the paper shows the results of applying and using of AIM numerically, also the results of the calculations show that the AIM is powerful and the spectrum of energy for hyperbolic single wave potential can be obtained for all energy states. The resulting energy levels of the AIM are not limited by the magnitude of the parameters ![]()
and ![]()
of the potential. Meanwhile, in the paper which has been done by H. Bahlouli, and A. D. Alhaidari found out that it is not so easy to obtain the energy spectrum for the potential by using the method which has been used to obtain the potential parameter spectrum, since it has to be inverted itself to obtain the energy spectrum, on the other hand, the inversion process is very hard to compute numerically the energy spectrum.
This paper aims to compute the energy spectrum which has not been computed in [8] [9] . To the best of our knowledge, this paper is the first study to compute the eigenenergies for the hyperbolic single wave potential. Before presenting the results, test where made to find out whether the AIM is suitable for finding the energy spectrum for hyperbolic single wave potential. Table 1, elucidate the rate of convergence of the AIM for![]()
, and![]()
. The result shows that for![]()
, the convergence takes place when![]()
, while for ![]()
the convergence takes place when![]()
.
Comparing these results with the results obtained through a private communication with the authors of [8] [9] which are![]()
, they were in a good agreement with them.
The conclusion to be drawn from this behavior which taken from Table 1, is that for the application of the method, the number of iterations depends on the degree of convergence required. In order to get accurate result for higher excited states, one needs to increase the number of iterations j for ![]()
until the convergence for ![]()
take place.
Table 2 a comparison between AIM results and numerical results obtained through a private communication with the authors of [8] [9] are made for the potential (1) with![]()
, ![]()
, and different values of the parameter![]()
, and it is found that the results obtained by AIM are in good agreement with the other.
![]()
Table 1. The rate of convergence of the AIM for the eigenenergies of the lowest states E0, E1 with hyperbolic single wave potential in Equation (1) with V0 = 5, λ = 0.2, γ = −0.4, and m = 1, computed for a number of iterations j.
![]()
Table 2. A comparison of the energy eigenvalues En of the potential (1) with λ = 1, V0 = −5, m = 1 and for different parameter γ.
In conclusion, AIM was used to obtain the energy spectrum hyperbolic single wave potential. One can note that the method gives the eigenvalues if one can transform the Schrödinger equation into a form of![]()
. The obtained numerical eigenenergies are in good agreement with the calculation results.
Acknowledgements
I would like to express my gratitude to Prof. H. Bahlouli, and Prof. A. D. Alhaidari for their valuable comments, encouragement, and discussion to complete this paper. Without their valuable efforts and guidance this paper wouldn’t have been accomplished.