1. Introduction
There are goods and service which have network effects. People obtain benefits if neighbors use it. The social local interaction can be represented by a network. Social network services and programming languages are examples of such goods with network effect. An existing goods has an advantage over new goods. The existing one is already in there and has network externality.
How can new goods beat the existing one under which condition(s), if any, new goods can beat existing ones? Does the structure of social network matter? We will address these questions. The goods and service with network effects can be modeled by a coordination game on networks. The networks are the social networks. Each player plays games with adjacent players only and derives payoff from each game. In a coordination game, a player obtains payoff if the player chooses the same strategy as that of the opponent. Such a coordination game on networks is the model for goods and service with network effects through social local interaction. We denote that a strategy prevails in the network if the strategy is chosen by more than half of the players. We study a coordination game with two strategies, A and B on networks. Suppose that all the players have the strategy B in the beginning and then we will show the condition for strategy A to beat the strategy B and to prevail in the network. The condition depends on the underlying network structures. If more than half of the players change their strategies, then new strategy beats the existing one in regular networks. On the other hand, if very small number of players with large degree change their strategies, then the new strategy beats the existing one in scale-free networks. More specifically, we will investigate the following problem.
1. In the beginning, all the players choose strategy B.
2. Then, the strategies of a fraction of players are changed from B to A.
3. After enough time steps, the state will arrive at either of the two distinct stable states.
(a) More than half of the players still take strategy B. The strategy B still prevails;
(b) More than half of the players change to the strategy A. The strategy A beats strategy B.
This situation is illustrated in Figure 1.
We will address the following questions:
1. What is the ratio of players who should change their strategies from B to A so that strategy A will prevail in the stable state?
2. Is the ratio dependent on network structure? Are they different between regular networks and scale-free networks in particular?
We will show that the network structure matters and that only small number of hub players determine whether new goods beat the existing strategy in scale-free networks. Scale-free networks are typical networks in reality. While more than half of the players must change their strategies from A to B for strategy A to prevail in regular networks, if small number of hub players change their strategies, then the strategy A prevails in scale-free networks.
This research is partly motivated by complex network researches. An academic interest in scale-free networks arose in late 1990’s (see the paper [1] ). Now it is recognized that outcomes of models including games on networks are dependent on network structures. In particular, interesting outcomes happen in scale-free networks because they have great network heterogeneity, which is the variance of degree distribution. One example is an epidemic spread model studies by [2] that investigates a contact network of an infectious disease. In regular networks, an epidemic spread occurs if and only if a certain condition is satisfied. On the other hand, it always breaks out in scale-free networks.
![]()
Figure 1. A blue vertex indicates strategy B, while a red vertex indicates strategy A. Initially, all the players choose strategy B and then strategies of a fraction of players are changed from B to A. In the next time step, two cases can occur by the network effect. In one case, some players return to strategy B, and strategy B prevails again. In the second case, other players choose strategy A, and strategy A prevails. Which occurs depends on the network structure and the fraction of changed players as we will show later.
2. Model
A player is on each vertex on a network. They play games with adjacent players only and derive payoff from each game. We will consider a pure coordination game, which means payoff from choosing the same strategy with adjacent player are the same regardless of the strategy A and B. We derive an average payoff from social interactions in some cases and we derive payoff from each social interaction in orther cases. We will study the latter case. To study this pure coordination game on networks is a good idea in order to investigate the condition that new goods beats the existing goods if they have network effect.
Let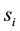 
denote the strategy of player i. We assume that 
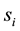takes either 
or 
without loss of generality. The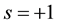 
corresponds to strategy A and 
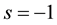to B. The payoff of the player i from the game with adjacent player j is given by
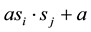. The payoff from choosing the same strategy is 2a and the payoff is 0 otherwise. Let 
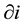denote the set of all players adjacent to player i. The payoff 
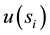of the player i is given by
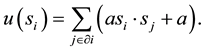(1)
A randomly chosen player updates the strategy in each time step. We assume that player i chooses the strategy with the following Logit probability:
(2)
where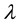 
is the payoff responsiveness parameter which can be understood as rationality. Such a functional form (2) has been used by several well-known papers, for example, [3] - [6] . We have a method to study network problem with this functional form. The mathematical structure itself is the same as that of the Ising model (see references such as [7] - [10] ). We solve the model by the method developed in order to solve the Ising model. Moreover, [6] solved the model by the same method that was developed earlier. After a while, the probability distribution of the strategy will be stable. This state is called stable state and we will focus on it.
3. Beating the Existing Strategy
If the mean strategy of all the players is positive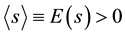
, strategy A prevails in the network; in other words, strategy A beats the existing strategy B. Degree is a number of links a vertex has. Let 
denote the fraction of players with degree 
whose strategies were changed from B to A, ![]()
denote the next neighbor degree, and ![]()
denote the next neighbor degree distribution. The point is that degree distribution of neighboring vertices and the degree distribution of the network are quite different. The probability that player i chooses strategy ![]()
is given by
![]()
(3)
where![]()
. We have the mean ![]()
of strategy as
![]()
(4)
Therefore, we have the following result.
Proposition 1: New strategy A will beat the existing strategy B if and only if ![]()
holds.
3.1. Two Ways of Changing the Strategy
The existing strategies are changed in either of following two ways.
Random replacement: Players change strategies from B to A randomly irrespective of the degree. If a fraction ![]()
of players change, we have ![]()
for all![]()
.
Selective replacement: Players change strategies from B to A according to a descending order of degree. We have
![]()
(5)
meaning if the degree of a vertex is larger than![]()
, the strategy of player is changed from B to A. If strategies of a fraction ![]()
of players are changed from B to A, ![]()
must satisfy
![]()
(6)
3.2. Regular Network
Every vertex has the same degree in regular networks, so elective replacement cannot be considered. We consi- der random replacement. Because of the condition ![]()
we have the following proposition.
Proposition 2: For new strategy A to beat the existing strategy B more than half of the players must change their strategies from B to A in random replacement for regular networks.
What does this imply? The best strategy for players to get the biggest payoff is to choose the strategy chosen by most of the neighbors. In random replacement, the strategies of more than half of the players are changed so that more than half of the neighbors of any player choose strategy A. This is not an effective way to beat the existing strategy since we must change the strategies of more than half of the players. From other respect, regular networks is robust.
3.3. Scale-Free Network
In random replacement, the condition remains the same as Proposition 2.
Proposition 3: For new strategy A to beat the existing strategy B more than half of the players must change their strategies from B to A in random replacement for scale-free networks.
Strategies of more than half of the players must be changed from B to A in scale-free networks. We will discuss selective replacement, wherein we have
![]()
. (7)
We also have![]()
. Because, in uncorrelated networks, the probability ![]()
that an end of a link is attached to a vertex with degree k is given by
![]()
(8)
We will calculate![]()
:
![]()
(9)
Suppose a fraction ![]()
of players change strategy from B to A; we have
![]()
(10)
which yields
![]()
(11)
The condition ![]()
turns out to be
![]()
(12)
Proposition 4:
In scale-free networks and in selective replacement, if more than a fraction ![]()
of players change their strategies from B to A, new strategy A beats the existing strategy B.
An example: Suppose we have a scale-free network with![]()
, and thus![]()
. If the strategies of only 1.56% players change, the strategy A beats the existing strategy B. In scale-free networks, only such a small number of players determine the strategy that prevails in the entire network. This is in sharp contrast to regular networks. Figure 2 illustrates the example, ![]()
of the scale-free one is smaller than ![]()
of the regular one in all the region. The ![]()
of the scale-free network where ![]()
is close to 2 is surprisingly small.
From one respect, scale-free networks are weak to selective replacement. If very small number of hub players changes their strategies, then most of the players change their strategies. On the other hand, scale-free networks are as robust as regular network in random replacement.
3.4. Numerical Simulations
We confirm the claims by numerical simulations. The payoff parameter![]()
, the rationality parameter![]()
, the mean degree![]()
, and the network size ![]()
are the same between the regular network and the
scale-free network for fair comparison. The simulation for regular network was done in the following way. In the beginning all the players are B-player meaning![]()
. Then, the strategy of one randomly chosen player is changed from B to A. After repeating the updates 50,000 times, we end the game. If less than 60% of the players become A-player in the end, we go on to the next game. In the next game, two randomly chosen players become A-player and the other players are B-player. We continue this process. If more than 60% of the players become A-player in the end, we finish the simulation. Suppose ![]()
players change to A-player in the beginning. The threshold is![]()
. In the simulation, the threshold is 0.480 which has good agreement with the theoretical value 0.5. Scale-free networks are constructed by the method of [1] [11] . The simulation for scale-free network is different in choosing the players who change the strategy from B to A in the beginning. We do the selective replacement. The strategies of players are changed from B to A in descending order of degree. We get the threshold for scale-free network. The result of the simulations are illustrated in Figure 3. The numerical simulation confirms the claims including Proposition 4.
![]()
Figure 2. The x axis indicate ![]()
of a scale-free and the y axis indi- cates ![]()
of a regular and a scale-free network.
![]()
Figure 3. The x axis indicate ![]()
of a scale-free and the y axis indi- cates ![]()
of a regular and a scale-free network. The circles are the results of simulations for scale-free networks and the dashed line is the result for regular network.
4. Concluding Remarks
We study goods and service with network effect. For this purpose, we study a coordination game with network structure. We study the condition that new goods and service replace the existing strategy. In regular networks, half of the players must be changed their strategies. On the other hand, it is enough for the new strategy to replace the existing strategy if small number of players with large degree changes their strategies. If![]()
, the number of the players is very small. Only small number of players determines the strategy of the entire network. It is meaningful to study models in scale-free networks because such a network is ubiquitous in reality. Indeed, many social networks in reality are scale-free. We reveal that scale-free networks and network heterogeneity drastically change outcomes.
NOTES
*Publication was supported by a grant-in-aid from Zengin foundation for studies on Economics and Finance.