Unsteady Magnetohydrodynamic Boundary Layer Flow near the Stagnation Point towards a Shrinking Surface ()
1. Introduction
Stagnation flow of an incompressible viscous fluid over a shrinking sheet has many important practical applications in engineering and industrial processes, such as the extrusion of a polymer in a melt-spinning process, continuous casting of metals, the aerodynamic extrusion of plastic sheets, the cooling of metallic sheets or electronic chips and many others. In all these cases, a study of fluid flow and heat transfer has important significance because the quality of the final product depends on the rate of cooling and the process of stretching.
In recent years, the boundary layer flow due to a shrinking sheet has attraction of many researchers because of its useful applications. A very interesting example in which the shrinking sheet situation occurs is of a rising shrinking balloon. Shrinking film is also a common application of shrinking sheet problems in engineering and industries. Shrinking film is very useful in packaging of bulk products because it can be unwrapped easily with adequate heat.
From the stretching case, the flow of shrinking sheet is different and the fluid is attracted towards a slot. Physically, the generated velocity at shrinking sheet has an unsteady flow due to the application of inadequate suction and is not confined within the boundary layer.
In view of all these applications, Sakiadis [1] initiated the study of boundary layer flow over a continuous solid surface moving with constant speed. Later Crane [2] considered the problem of the flow over a linearly stretching sheet in an ambient fluid and gave a similarity solution in closed analytical form for the steady two-dimensional problem. Gupta and Gupta [3] , and Vleggaar [4] have investigated the solution of stretching flow problems at the constant surface temperature while Soundalgekar and Ramana [5] and Grubka and Bobba [6] have analysed the solution of stretching flow problems with a variable surface temperature. Many researchers such as Magyari and Keller [7] , Elbashbeshy and Bazid [8] , Jat and Chaudhary [9] -[11] , Bachok et al. [12] and Zheng et al. [13] have analyzed the stretching sheet problems with different aspects of fluid, such as the heat transfer, the permeability of the surface and the unsteadiness flow. Mahapatra and Nandy [14] [15] studied the unsteady stagnation-point flow and heat transfer over an unsteady shrinking sheet. Recently Aly and Vajravelu [16] and Chaudhary and Kumar [17] discussed numerical solutions of boundary layer flow problems over different surfaces in a porous medium. More recently Nandy et al. [18] and Rosca and Pop [19] investigated the unsteady boundary layer flow over a permeable stretching or shrinking surface.
Realizing the increasing technical applications of the magnetohydrodynamic effects, the aim of the present work is concerned with a steady, two-dimensional unsteady stagnation flow of an electrically conducting fluid over a shrinking surface in the presence of a uniform transverse magnetic field.
2. Formulation of the Problem
Consider an unsteady two-dimensional steady flow  of a viscous incompressible electrically conducting fluid near a stagnation point over a continuously shrinking surface placed in the plane
of a viscous incompressible electrically conducting fluid near a stagnation point over a continuously shrinking surface placed in the plane 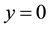 of a Cartesian coordinate system in the presence of time dependent free stream. The x-axis is taken along the shrinking surface in the direction of motion and y-axis is perpendicular to it. A uniform magnetic field of constant strength
of a Cartesian coordinate system in the presence of time dependent free stream. The x-axis is taken along the shrinking surface in the direction of motion and y-axis is perpendicular to it. A uniform magnetic field of constant strength 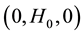 is assumed to be applied normal to the shrinking surface (Figure 1). The surface is assumed to be
is assumed to be applied normal to the shrinking surface (Figure 1). The surface is assumed to be
![]()
Figure 1. Coordinate system for the shrinking surface.
highly elastic and is shrinking in the x-direction with a velocity is 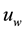 and surface temperature
and surface temperature 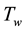 while the velocity of the flow, external to the boundary layer is
while the velocity of the flow, external to the boundary layer is 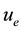 and temperature
and temperature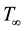 . Therefore, under the usual boundary layer and Boussinesq approximations, the systems of boundary layer equations are given by
. Therefore, under the usual boundary layer and Boussinesq approximations, the systems of boundary layer equations are given by
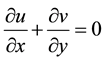 (1)
(1)
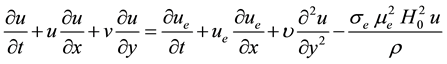 (2)
(2)
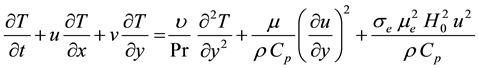 (3)
(3)
where 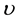 is the coefficient of kinematic viscosity,
is the coefficient of kinematic viscosity, 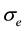 the electrical conductivity,
the electrical conductivity, 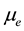 the magnetic permea-
the magnetic permea-
bility, 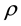 the density, Pr the Prandtl number
the density, Pr the Prandtl number ,
, ![]() the coefficient of viscosity,
the coefficient of viscosity, ![]() the specific heat at constant pressure and
the specific heat at constant pressure and ![]() the thermal conductivity. The other symbols have their usual meanings.
the thermal conductivity. The other symbols have their usual meanings.
The boundary conditions are
![]() (4)
(4)
where c is a constant, ![]() is the shrinking rate and a is the strength of the stagnation point flow.
is the shrinking rate and a is the strength of the stagnation point flow.
3. Analysis
The continuity Equation (1) is identically satisfied by stream function![]() , defined as
, defined as
![]() (5)
(5)
For the solution of the momentum and the energy Equations (2) and (3), the following dimensionless variables are defined:
![]() (6)
(6)
![]() (7)
(7)
![]() (8)
(8)
Equations (5) to (8), transform Equations (2) and (3) into
![]() (9)
(9)
![]() (10)
(10)
where a prime (') denotes differentiation with respect to![]() ,
, ![]() is the unsteadiness parameter,
is the unsteadiness parameter, ![]() is the velocity parameter,
is the velocity parameter, ![]() is the Magnetic parameter and
is the Magnetic parameter and ![]() is the Eckert number.
is the Eckert number.
The corresponding boundary conditions are
![]() (11)
(11)
For numerical solution of the Equations (9) and (10), through a perturbation technique, by assuming the following power series in a small magnetic parameter ![]() as
as
![]() (12)
(12)
![]() (13)
(13)
Substituting Equations (12) and (13) and its derivatives in Equations (9) and (10) and then equating the coefficients of like powers of![]() , we get the following set of equations
, we get the following set of equations
![]() (14)
(14)
![]() (15)
(15)
![]() (16)
(16)
![]() (17)
(17)
![]() (18)
(18)
![]() (19)
(19)
with the boundary conditions
![]() (20)
(20)
The Equation (14) is obtained by Mahapatra and Nandy [14] for the non-magnetic case and the remaining equations are ordinary linear differential equations and have been solved numerically by Runge-Kutta method of fourth order. The velocity and temperature distributions for various values of parameters are shown in Figure 2 to Figure 6 respectively.
4. Skin Friction and Surface Heat Transfer
The physical quantities of interest, the local skin friction coefficient ![]() and the local Nusselt number Nu i.e. surface heat transfer are given by:
and the local Nusselt number Nu i.e. surface heat transfer are given by:
![]() (21)
(21)
![]()
Figure 2. Velocity distribution against η for various values of β and Rem with![]() .
.
and
![]() (22)
(22)
which, in the present case can be expressed in the following forms
![]() (23)
(23)
and
![]() (24)
(24)
where ![]() is the local Reynolds number.
is the local Reynolds number.
Numerical values of the functions ![]() and
and![]() , which are proportional to local skin friction and local heat transfer rate at the surface respectively for various values of the parameter are presented in Table 1 and Table 2.
, which are proportional to local skin friction and local heat transfer rate at the surface respectively for various values of the parameter are presented in Table 1 and Table 2.
![]()
Table 1. Numerical values of ![]() for various values of the parameters β, α & Rem.
for various values of the parameters β, α & Rem.
![]()
Table 2. Numerical values of ![]() for various values of the parameters β, α, Rem, Pr & Ec.
for various values of the parameters β, α, Rem, Pr & Ec.
5. Results and Discussion
Figure 2 shows the variation of velocity distribution against η for various values of the unsteadiness parameter β, the velocity parameter α and the magnetic parameter Rem. It may be observed that, for the fixed value of the velocity parameter α velocity distribution increases with the decreasing value of the unsteadiness parameter β, and opposite phenomenon occur for the magnetic parameter Rem, for a fixed η.
Figure 3 to Figure 6 show the variation of temperature distribution against η for the various values of the parameters such as the unsteadiness parameter β, the velocity parameter α, the magnetic parameter Rem, the Prandtl number Pr and the Eckert number Ec. From these figures it may be observed that the temperature distribution decreases with increasing values of the unsteadiness parameter β, the velocity parameter α, the magnetic parameter Rem, the Prandtl number Pr and the Eckert number Ec.
In Table 1, the numerical values of the function ![]() for various values of the unsteadiness parameter β, the velocity parameter α and the magnetic parameter Rem are given. It may be observed from the table that the boundary values
for various values of the unsteadiness parameter β, the velocity parameter α and the magnetic parameter Rem are given. It may be observed from the table that the boundary values ![]() for the non-magnetic flow are the same as those obtained by Mahapatra and Nandy [14] . The value of the function
for the non-magnetic flow are the same as those obtained by Mahapatra and Nandy [14] . The value of the function ![]() decreases with the increasing values of the unsteadiness parameter β and the magnetic parameter Rem respectively taking other parameters constant and reverse phenomenon occurs for the velocity parameter α.
decreases with the increasing values of the unsteadiness parameter β and the magnetic parameter Rem respectively taking other parameters constant and reverse phenomenon occurs for the velocity parameter α.
In Table 2, the numerical values of the function ![]() for the different values of the unsteadiness parameter β, the velocity parameter α, the magnetic parameter Rem, the Prandtl number Pr and the Eckert number Ec are given. It may be observed from the table that the boundary values
for the different values of the unsteadiness parameter β, the velocity parameter α, the magnetic parameter Rem, the Prandtl number Pr and the Eckert number Ec are given. It may be observed from the table that the boundary values ![]() for the non-magnetic flow are same as those obtained by Mahapatra and Nandy [14] . The value of the function
for the non-magnetic flow are same as those obtained by Mahapatra and Nandy [14] . The value of the function ![]() increases with the increasing value of the unsteadiness parameter β, considering other parameters constant and same phenomenon occurs for the velocity parameter α, the magnetic parameter Rem, the Prandtl number
increases with the increasing value of the unsteadiness parameter β, considering other parameters constant and same phenomenon occurs for the velocity parameter α, the magnetic parameter Rem, the Prandtl number ![]() and the Eckert number Ec. It is further observed that the function
and the Eckert number Ec. It is further observed that the function ![]() decreases with an increasing value of the Prandtl number
decreases with an increasing value of the Prandtl number ![]() for fixed other parameters.
for fixed other parameters.
6. Conclusions
The present work extends the two-dimensional unsteady stagnation flow of an electrically conducting fluid, over shrinking surface in the presence of magnetic field. Under some special conditions, the problem will reduce the results obtained by previous researchers. The effects of different parameters such as the unsteadiness parameter, the velocity parameter, the magnetic parameter, the Prandtl number and the Eckert number are studied in detail. The velocity as well as thermal boundary layer thickness decreases with the increasing values of the unsteadiness parameter, the velocity parameter, the magnetic parameter, the Prandtl number and the Eckert number whereas in the velocity reverse phenomenon occurs for the magnetic parameter. From the results it can be concluded that skin friction and Nusselt number vary according to the velocity and thermal boundary layers thickness respectively with different parameters.