1. Introduction
Quarkonium in particle physics refers to meson whose constituents are a quark and its own antiquark. The famous quarkonium system is charmonium and bottomonium. Bottomonium 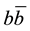 meson has discovered recently with the ATLAS detector at the Large Hadron Collider (LHC) [1] . Bottomonium family is the set of particles that contain both a bottom quark and an anti-bottom quark but are bound together with different energies. A number of botommonium properties are well described by the quark model [2] - [8] where mesons have quantum numbers
meson has discovered recently with the ATLAS detector at the Large Hadron Collider (LHC) [1] . Bottomonium family is the set of particles that contain both a bottom quark and an anti-bottom quark but are bound together with different energies. A number of botommonium properties are well described by the quark model [2] - [8] where mesons have quantum numbers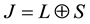 ,
, 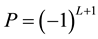 and
and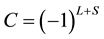 ;
; 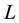 and
and 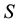 are the quantum numbers for the quark-anti- quark orbital angular momentum and their net spin angular momentum respectively [9] . The main aim of our work is to study the spectra of heavy mesons and the corresponding wave functions. Bottomonium
are the quantum numbers for the quark-anti- quark orbital angular momentum and their net spin angular momentum respectively [9] . The main aim of our work is to study the spectra of heavy mesons and the corresponding wave functions. Bottomonium  spectra, as an example of heavy meson, are investigated by using matrix Numerov’s method [10] [11] via non-relativistic potential model [12] - [14] . However, a vast majority of numerical methods have been used to solve the Schrödinger equation (SE) numerically, for instance, Runge-Kutta method [15] , Shooting method [16] , Numerov’s method [17] , four-step exponentially fitted method [18] and the factorization method [19] . But, here we show that the matrix Numerov’s algorithm is a more efficient and fast one to achieve our goal; we hope this approximation gives the reliability features of heavy meson investigation. Moreover, the heavy-meson wave functions determined in this work can be employed to make predictions of other properties. On the other hand, the main motivation is to calculate the root mean square radius
spectra, as an example of heavy meson, are investigated by using matrix Numerov’s method [10] [11] via non-relativistic potential model [12] - [14] . However, a vast majority of numerical methods have been used to solve the Schrödinger equation (SE) numerically, for instance, Runge-Kutta method [15] , Shooting method [16] , Numerov’s method [17] , four-step exponentially fitted method [18] and the factorization method [19] . But, here we show that the matrix Numerov’s algorithm is a more efficient and fast one to achieve our goal; we hope this approximation gives the reliability features of heavy meson investigation. Moreover, the heavy-meson wave functions determined in this work can be employed to make predictions of other properties. On the other hand, the main motivation is to calculate the root mean square radius 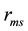 of different states for bottomonium and the numerical values of
of different states for bottomonium and the numerical values of 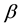 coefficient, which can be used to calculate the decay widths [20] , and differential cross sections [21] for quarkonium states. Besides, an additional aim of our work is to investigate the mass-radius dependence for states of bottomonium. The remainder of this paper is organized as follows. In Section 2, we present some characteristics properties of bottomonium mesons which in turn depend on the potential model. In Section 3, we present our main problem and its analytic solution. In Section 4, results and discussion are given. Finally in the last section, we summarize our main results and conclusions.
coefficient, which can be used to calculate the decay widths [20] , and differential cross sections [21] for quarkonium states. Besides, an additional aim of our work is to investigate the mass-radius dependence for states of bottomonium. The remainder of this paper is organized as follows. In Section 2, we present some characteristics properties of bottomonium mesons which in turn depend on the potential model. In Section 3, we present our main problem and its analytic solution. In Section 4, results and discussion are given. Finally in the last section, we summarize our main results and conclusions.
2. Characteristics of Bottomonium Mesons
2.1. The Potential Model of Bottomonium Mesons
One of the most successful ways of describing the quarkonium system is to solve the non-relativistic Schrödinger equation for these quark-anti quark states with an appropriate potential model. In a non-relativistic constituent quark model, one ignores the dynamical effects of gluon fields on the hadrons structure and properties. Quarks are considered as non-relativistic objects interacting via an instantaneous adiabatic potential provided by gluons, and the non relativistic description with the Schrödinger equation gives acceptable results.
Thus, the potential model used here [22] [23] is written as:
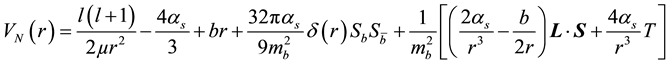 (1)
(1)
where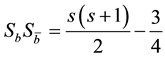 ,
, 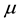 is the reduced mass of the quark and anti-quark,
is the reduced mass of the quark and anti-quark, ![]() is the mass of the bottom
is the mass of the bottom
quark, and S is the total spin quantum number of the meson. For the ![]() mesons, the parameters
mesons, the parameters![]() ,
, ![]() ,
, ![]() , and
, and ![]() are taken to be 0.4036, 0.1624 GeV, 2.4948 GeV and 4.8097 GeV respectively [24] .
are taken to be 0.4036, 0.1624 GeV, 2.4948 GeV and 4.8097 GeV respectively [24] . ![]() is the tensor operator and the spin-orbit operator is diagonal in a
is the tensor operator and the spin-orbit operator is diagonal in a ![]() basis [9] , with the matrix elements.
basis [9] , with the matrix elements.
![]()
2.2. Wave Functions of Bottomonium Mesons
Bottomonium mesons can be described by the wave function of the bound quark-antiquark state which satisfies the SE by using the potential given in Equation (1). Radial Schrödinger equation, ![]() , is written (in natural units) as:
, is written (in natural units) as:
![]() (2)
(2)
where ![]() is the radial wave function,
is the radial wave function, ![]() is the inter quark distance,
is the inter quark distance, ![]() is the sum of kinetic and potential of quark-antiquark system, and
is the sum of kinetic and potential of quark-antiquark system, and ![]() and
and ![]() are defined above through Equation (1). The matrix Numerove’s method is used to solve Equation (1) to get spectra of bottomonium, the detailed of this method could be found in Ref. [11] . In the following sections, we employ that method to obtain the wave functions of bottomonium.
are defined above through Equation (1). The matrix Numerove’s method is used to solve Equation (1) to get spectra of bottomonium, the detailed of this method could be found in Ref. [11] . In the following sections, we employ that method to obtain the wave functions of bottomonium.
3. Basic Properties of Bottomonium Meson
3.1. Bottomonium Root Mean Square Radius ![]()
Define Bottomonium root mean square radius ![]() is one of basic properties of bottomonium. If the distance between the quark and anti-quark in bottomonium is
is one of basic properties of bottomonium. If the distance between the quark and anti-quark in bottomonium is ![]() fm it may be regarded that bottomonium has radius
fm it may be regarded that bottomonium has radius ![]() fm where
fm where ![]() is the distance from the point quark to anti-quark.
is the distance from the point quark to anti-quark. ![]() can be derived from the meson wave function and may be written as [25] .
can be derived from the meson wave function and may be written as [25] .
![]() (3)
(3)
3.2. β Coefficient
The meson wave function is characterized by a momentum width parameter ![]() that is related to the root mean square quark-antiquark separation
that is related to the root mean square quark-antiquark separation ![]() of the meson by [26] .
of the meson by [26] .
![]() (4)
(4)
where ![]() is the principal quantum number and
is the principal quantum number and ![]() is the sub-atomic energy level number. The parameter
is the sub-atomic energy level number. The parameter ![]() is typically taken as a parameter of the model. However, since we are seeking for describing the decay of heavy quark states, it is preferable to reproduce
is typically taken as a parameter of the model. However, since we are seeking for describing the decay of heavy quark states, it is preferable to reproduce ![]() coefficient of the quark model states. These values of
coefficient of the quark model states. These values of ![]() are obtained for the first time. So, we suggest using it to calculate the decay width of heavy quarkonium states.
are obtained for the first time. So, we suggest using it to calculate the decay width of heavy quarkonium states.
4. Results and Discussion
A non-relativistic potential model is used to study some properties of bottomonium meson by using the matrix Numerov’s method. The eigenvalues and the corresponding wave functions are found by using the same method. Then we normalized the wave functions and found the root mean square radius of bottomonium mesons by using Equation (3). Moreover, we can obtain computational values of ![]() coefficient by using Equation (4). The normalized radial wave functions for bottomonium mesons are graphically represented in Figures 1-3 respectively. For bottomonium mesons, our calculated masses and root mean square radius are reported in Table 1 in case of S, P and D States respectively. We observe that our results are in good agreement with the experiment [27] and existing theoretically predicted values [24] , which shows the validity of the used method. Some of our calculated root mean square radii are found to be in good agreement with the published one of ref. [28] . The
coefficient by using Equation (4). The normalized radial wave functions for bottomonium mesons are graphically represented in Figures 1-3 respectively. For bottomonium mesons, our calculated masses and root mean square radius are reported in Table 1 in case of S, P and D States respectively. We observe that our results are in good agreement with the experiment [27] and existing theoretically predicted values [24] , which shows the validity of the used method. Some of our calculated root mean square radii are found to be in good agreement with the published one of ref. [28] . The ![]() values could be used to calculate the decay constants [29] , decay widths [29] , and differential cross sections [30] for quarkonium states with high accuracy as we used complicated potential model. The predictions about these quantities are also reported in Table 1 for bottomonium S, P, and D States respectively. Finally, we investigated the mass-radius dependence for states of bottomonium. We confirmed a leading linear relation between masses
values could be used to calculate the decay constants [29] , decay widths [29] , and differential cross sections [30] for quarkonium states with high accuracy as we used complicated potential model. The predictions about these quantities are also reported in Table 1 for bottomonium S, P, and D States respectively. Finally, we investigated the mass-radius dependence for states of bottomonium. We confirmed a leading linear relation between masses
![]()
Figure 1. Bottomonium S-states reduced radial wave functions plotted together with used potential.
![]()
Figure 2. Bottomonium P-states reduced radial wave functions plotted together with used potential.
![]()
Figure 3. Bottomonium D-state reduced radial wave functions plotted together with used potential.
and the radius for bottomonium and found that, with the exception of the 1S-state, the linear relation is also a good approximation for bottomonium. The relation between mass and radius in case of S-state, P-state and D-state are shown in Figure 4. Moreover, the mass-radius relation for bottomonium ![]() in case of P-state and D-state are shown in Figure 5. It is easily to behold that the S-state seems to be special as it is, in contrast to the other states. It worth noting that, a linear dependence of mass and radius might only be a good guess for states other than the S-state.
in case of P-state and D-state are shown in Figure 5. It is easily to behold that the S-state seems to be special as it is, in contrast to the other states. It worth noting that, a linear dependence of mass and radius might only be a good guess for states other than the S-state.
5. Summary and Conclusion
Bottomium ![]() is predicted by the standard model of particle physics but other models and techniques are required to calculate the particles’ properties. The bottomium
is predicted by the standard model of particle physics but other models and techniques are required to calculate the particles’ properties. The bottomium ![]() meson spectroscopy is studied experimentally
meson spectroscopy is studied experimentally
![]()
Figure 4. The relation between theoretical spectrum and root mean square ![]() of P and D bottomonium states.
of P and D bottomonium states.
![]()
Figure 5. The relation between theoretical spectrum and root mean square ![]() of S, P and D bottomonium states. The S-state data has not been included in fitting.
of S, P and D bottomonium states. The S-state data has not been included in fitting.
according to PDG [27] . In this work we use the matrix Numerov’s method to obtain the radial wave functions of bottomonium meson to calculate the bottomonium ![]() root mean square
root mean square ![]() and
and ![]() coefficient. As a remarkable result, we can point out that it is recommended to use the obtained values of
coefficient. As a remarkable result, we can point out that it is recommended to use the obtained values of ![]() and
and ![]() coefficient to calculate the decay widths and differential cross sections for bottomonium system. We indicate a high level of accuracy by comparing the results of decay width with available published results of decay width. Moreover, the matrix Numerov’s method [11] is tested again to obtain some mesons properties. The obtained results are in good agreement with the published data [28] . Then, the method could be safely used to solve SE. In addition, the relation between theoretical masses we obtained and
coefficient to calculate the decay widths and differential cross sections for bottomonium system. We indicate a high level of accuracy by comparing the results of decay width with available published results of decay width. Moreover, the matrix Numerov’s method [11] is tested again to obtain some mesons properties. The obtained results are in good agreement with the published data [28] . Then, the method could be safely used to solve SE. In addition, the relation between theoretical masses we obtained and ![]() values have been drawn. As pointed out previously, the fitted straight line reflects perfectly the dependence of mass and radius. Eventually, we may notice that the calculated values of
values have been drawn. As pointed out previously, the fitted straight line reflects perfectly the dependence of mass and radius. Eventually, we may notice that the calculated values of ![]() and other parameters are the newer outputs where we didn’t find others for comparison. So, we are looking forward to take these data in consideration by other experimental or theoretical researchers.
and other parameters are the newer outputs where we didn’t find others for comparison. So, we are looking forward to take these data in consideration by other experimental or theoretical researchers.