To Problem of the Rewinding of the Tape with Automatically Adjustable Influences ()
1. Introduction
For the first time the concept idea of servo-constraints has been entered into analytical dynamics by H. Beghin [1] . The methods used by H. Beghin, had the further development in P. Appel’s [2] works, A. Przeborski’s [3] , V. S. Novoselov’s [4] , M. F. Shulgin’s [5] , V. V. Rumjantsev’s [6] [7] , V. I. Kirgetov’s [8] , A. G. Azizov’s [9] [10] and others.
Appendices of methods of analytical dynamics to a wide range of specific targets demand the account and other features connected with steady realization of servo-constraints, and that for such systems it is impossible to distract from a way of their realization.
S. S. Nugmanova’s attention for the first time has been paid to this circumstance [11] . Following the theory of parametrical clearing [12] , and the theory of the compelled motions [13] constructed the theory, allowing to develop the area of practical applicability of methods of analytical mechanics of systems with servo-constraints, including questions of their steady realization [14] [15] . In works [16] [17] the equations of motion of the systems, interfered by constraints of the first and second sort are deduced, and also the obvious kind of forces of reactions of servo-constraints is defined.
In this article the results of works [16] [17] are illustrated to the problem of rewinding of a tape.
2. Forming the Equation of Motion and Refining the Servo-Constraints’ Forces of Reaction
Let’s consider process of rewinding of a tape (Figure 1). Rewinding of a tape from the drum 3 on a drum 2 is carried out by means of electric machine (EM) of a direct current of the independent excitation operating through a reducer with transfer number  on a drum 2. On Figure 1 the feedback providing a constancy of linear speed of motion of tape u = сonst and forming of stabilizing pressure on an input of the electric machine (EM) are illustrated. As well as, from the work of Zijatdinov R. M. (1983) [18] , we will divide the scheme Fig- ure 1 on two parts on a dashed line. Kinetic energy of system looks like as:
on a drum 2. On Figure 1 the feedback providing a constancy of linear speed of motion of tape u = сonst and forming of stabilizing pressure on an input of the electric machine (EM) are illustrated. As well as, from the work of Zijatdinov R. M. (1983) [18] , we will divide the scheme Fig- ure 1 on two parts on a dashed line. Kinetic energy of system looks like as:
 (1)
(1)
where ―the moments of inertia of a reducer both corresponding drums;
―the moments of inertia of a reducer both corresponding drums;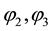 ―angles of rotation of drums 2 and 3.
―angles of rotation of drums 2 and 3.
As drums 2 and 3 represent bodies of variable weight it is necessary to take the general equation of dynamics in the form showed in Bessonov A. P. (1967) [19] :
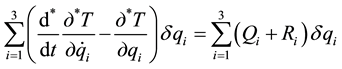 (2)
(2)
where for  co-ordinates
co-ordinates 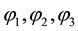 are designated;
are designated; −the generalized force appropriated to co-ordinate
−the generalized force appropriated to co-ordinate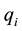 ;
;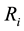 ―the generalized reactive force, which looks like
―the generalized reactive force, which looks like
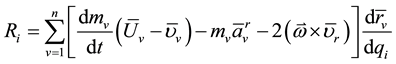
here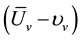 ―relative speed of joining particles;
―relative speed of joining particles;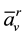 ―particle acceleration in motion concerning the system of co-ordinates connected by a link, and the symbol “*” above specifies that differentiation is made according to a hardening principle.
―particle acceleration in motion concerning the system of co-ordinates connected by a link, and the symbol “*” above specifies that differentiation is made according to a hardening principle.
![]() FM−forwarding mechanism; EM−electric machine; ES−energy source; RC−rein forcer-changer; CCP−converter of code in pressure; CS−converter scheme; DWM−digital watching machine; MG−measuring gauge.
FM−forwarding mechanism; EM−electric machine; ES−energy source; RC−rein forcer-changer; CCP−converter of code in pressure; CS−converter scheme; DWM−digital watching machine; MG−measuring gauge.
Figure 1. Process of rewinding of a tape.
If relative speed of joining particles is equal to zero, and there is no relative motion of joining particles concerning a drum 2, according to Bessonov A. P. [16] (1967) we conclude that:
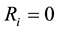
On system, according to assumptions, one ideal geometrical constraint
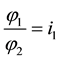 (3)
(3)
and one kinematical servo-constraint in Beghin H. (1967) [1]
![]() (4)
(4)
is imposed, where![]() −radius of an empty drum 2;
−radius of an empty drum 2;![]() −a thickness of a tape.
−a thickness of a tape.
Taking into account (3) kinetic energy (1) systems we will lead to a formula
![]() (5)
(5)
On possible moving constraint (3) imposes restriction [7] :
![]() (6)
(6)
From a way of action of servo-constraint (4) follows that, moving, on which servo-constraint works do not make reaction, look like in Beghin H. (1967) [1] :
![]() (7)
(7)
We will consider the right part from a dashed line. Considering that for the right part,
![]() (8)
(8)
where![]() −the constant moment put EM under the influence of direct current;
−the constant moment put EM under the influence of direct current;![]() −force of a tension of a tape, from (2), (5)-(8), by method (A)-moving [6] [7] , we will receive:
−force of a tension of a tape, from (2), (5)-(8), by method (A)-moving [6] [7] , we will receive:
![]() (9)
(9)
where![]() −reaction of servo-constraint (4).
−reaction of servo-constraint (4).
Considering that for the left part
![]() (10)
(10)
where![]() −radius of no to wind off drum 3;
−radius of no to wind off drum 3;![]() −the brake moment of a drum 3, from (5), (10) we will receive
−the brake moment of a drum 3, from (5), (10) we will receive
![]() (11)
(11)
To the received system of the Equations (9), (11) adding one kinematical equation,
![]() (12)
(12)
will be received system of three Equations (9), (11), (12) concerning unknown persons![]() .
.
Consider a case, when rewinding is carried out with constant brake moment![]() , and speed of a tape
, and speed of a tape ![]() is regulated only.
is regulated only.
As it is known [9] [10] , servo-constraints are carried out not precisely and therefore, along with (4) the have occurrence parity
![]() (13)
(13)
where![]() −the parameter, characterizing clearing of system from servo-constraint (4).
−the parameter, characterizing clearing of system from servo-constraint (4).
Having for an object steady realization of servo-constraint (4), the received system of the equations will be added to (9), (11), (12) equation [9] [10] :
![]() (14)
(14)
and reaction compulsion ![]() we set in a kind,
we set in a kind,
![]() (15)
(15)
where![]() −a positive constant at the expense of which choice there is a possibility to satisfy to quality of transient [19] [20] . Taking into account (3), (15), Equation (14) we will lead to the following:
−a positive constant at the expense of which choice there is a possibility to satisfy to quality of transient [19] [20] . Taking into account (3), (15), Equation (14) we will lead to the following:
![]() (16)
(16)
Thus, the system of the Equations (9), (11), (12), (16) describes dynamics of adjustable process of rewinding of a tape concerning variables![]() . From system of the Equations (9), (11), (12), (16) can be defined
. From system of the Equations (9), (11), (12), (16) can be defined ![]() as function of variables
as function of variables![]() , and by that reaction of servo-constraint in the form of the feedback law. For this purpose from the Equation (11) we will define force
, and by that reaction of servo-constraint in the form of the feedback law. For this purpose from the Equation (11) we will define force![]() :
:
![]() ,
,
and substituting it in (9), the following equation will be received:
![]() (17)
(17)
Taking into account (12), Equation (17) can be led to the following:
![]()
3. Stability
If a reaction of servo-constraint ![]() to form under the law, showed in [17] [18] :
to form under the law, showed in [17] [18] :
![]()
where![]() −a positive constant, the Equation (18) is led to a kind:
−a positive constant, the Equation (18) is led to a kind:
![]()
Taking into account a parity (13), last equation will look like:
![]() (19)
(19)
Considering![]() , from (19) we will receive
, from (19) we will receive
![]() (20)
(20)
Taking into account (20), Equation (19) will look like
![]() (21)
(21)
where
![]() (22)
(22)
Apparently, from (22) the Equation (21) represents the differential equation with variable factors. Stability of its zero decision ![]() it is going to be investigated by a method of functions of Lyapunov, developed for unsteady systems [16] [17] . The auxiliary equation to (21) will look like:
it is going to be investigated by a method of functions of Lyapunov, developed for unsteady systems [16] [17] . The auxiliary equation to (21) will look like:
![]() (23)
(23)
where
![]() (24)
(24)
In expression (24) constant number ![]() we will choose such, that a root
we will choose such, that a root ![]() of the characteristic Equation (23)
of the characteristic Equation (23)
![]()
had a negative material part. This condition, according to Hurvits’s criterion [21] , will look like
![]()
which is reduced to a condition
![]() (25)
(25)
Lyapunov’s definitely positive function ![]() will be chosen as:
will be chosen as:
![]() .
.
Its full derivative on time, worked out owing to the equation of the indignant motion (23), will look like:
![]()
Let’s calculate: ![]()
![]() .
.
Then the condition of certain positively of the form―![]() will look like
will look like
![]()
which it is reduced to a condition
![]() (26)
(26)
Condition (26) show that, for maintenance of steady realization of servo-constraint (4) moment of the electric machine ![]() (EM), the moment of friction
(EM), the moment of friction![]() , the moments of inertia
, the moments of inertia ![]() and a positive constant
and a positive constant ![]() it is necessary to choose on corresponding condition.
it is necessary to choose on corresponding condition.
4. The Realization of Servo-Constraints
We will consider a realization problem of servo-constraint (4) by electromechanical digital watching system (DWS) [20] for which executive element we accept the engine of a direct current of independent excitation. Its full system of the equations will look like [17] :
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() (27)
(27)
where![]() −inductive and ohmic resistance EM;
−inductive and ohmic resistance EM;![]() −delay factors;
−delay factors;![]()
![]() −strengthening factors;
−strengthening factors;![]() −factor against-EDS and the rotary moment;
−factor against-EDS and the rotary moment;![]() − entrance pressure EM;
− entrance pressure EM;![]() −target pressure of the converter of code in pressure (CCP);
−target pressure of the converter of code in pressure (CCP);![]() −target parameter DWM;
−target parameter DWM;![]() ,
, ![]() ,
,![]() −target parameters of gauges measurements (MG) and schemes of transformations (converter scheme) (CS); the moment of inertia of anchor of EM;
−target parameters of gauges measurements (MG) and schemes of transformations (converter scheme) (CS); the moment of inertia of anchor of EM; ![]() −some function of the arguments.
−some function of the arguments.
The law of formation of the operating influences DWM providing stability of motion of system in relation to servo-constraint (4) is defined by the decision of system of the equations:
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() (28)
(28)
rather of![]() . This law looks like:
. This law looks like:
![]() (29)
(29)
Substituting the law (29) in (27), results the Equation (21). Hence, the law (28) provides asymptotically stability of motion of system under the relation of the variety defined by servo-constraint (4).
Along with the generalized model, we will consider the simplified model of watching system [17] [18] , i.e. at assumptions,
![]() , (30)
, (30)
from (28) we will receive the law of formation of operating influences DWM for simplified model DWS:
![]() (31)
(31)
Substituting the law (31) in (27) at the same assumptions (30) we will receive the Equation (21), which stability conditions looks like (26).