Application of the Method of Characteristics to Population Balance Models Considering Growth and Nucleation Phenomena ()
1. Introduction
Pharmaceutical, chemical and food industries produce significant amount of materials in crystalline form. Crystallization is an important separation unit in these industries, and has a significant impact on plant operation and economics. Crystal size distribution is an important quality aspect of the crystalline product. The industrial crystallization process faces a major challenge for the production of crystals of predefined size distribution. Dynamic modeling of crystallization process has received notable consideration in recent time due to its various applications [1] . The population balance modeling is a widely accepted mathematical frame work for dynamic modeling of this process. Hulbert and Katz [2] are the main architects of population balance modeling. The approach has capability to simulate the crystallization process and to describe the evolution of each individual crystal throughout the process.
On the other hand, accurate numerical solution of the population balance equation (PBE) is a challenging task for several reasons. Numerical diffusion and instability are common problems in the numerical solutions of PBEs for seeded batch systems. Incompatibility between the initial and the boundary conditions is one reason of the aforementioned problem. The number density distribution of seeds is unlikely to be the same to that generated by nucleation process. If their values match, the first order derivative of the distribution may not be identical. This can lead to sharp discontinuities that are rapidly broadened by numerical diffusion. Another problem that is usually encountered in the solution of PBEs is the occurrence of steep moving fronts, known as source of numerical instability. This problem arises from the convective nature of growth-dominated process [1] . Several researchers in this filed have tried to develop specified algorithms for tackling these complexities. A verity of accurate and efficient numerical techniques were introduced, such as the finite difference methods [3] [4] , the method of moments [5] [6] , the method of weighted residuals [7] , the Monte Carlo method [8] , and the flux limiting high resolution finite volume schemes [9] -[11] . In this article, the method of characteristics (MOC) [1] [12] -[14] is applied to solve the PBE for simulating crystallization process. The MOC has capability to avoid numerical diffusion and instabilities in the solutions on coarse meshes and has low computational cost. These virtues encourage its applicability to industrial processes. The MOC transforms the given PBE into a system of ordinary differential equations (ODEs), which are then solved along the path line of the particles (characteristic curves). The particles are identified and located at the initial time and the population is trailed with a velocity equal to the growth rate.
This article is organized as follows. In Section 2, the population balance modeling of batch crystallization process is briefly introduced. In Section 3, the method of characteristics is derived. This is followed by Section 4 in which the forgoing numerical technique is applied to four test problems. Finally, the concluding remarks are outlined in Section 5.
2. Batch Crystallization Model
In the one-dimensional batch crystallization model, the crystal size is defined by a characteristic length l. The crystal size distribution (CSD) is depicted by the number density function  which denotes the number of crystals per crystal length at any time t. The crystal growth rate G could be either dependent or independent of crystal size. Balancing the number of crystals in an infinitesimal interval of crystal length, a partial differential equation is obtained which explains the temporal evolution of CSD [12] [15]
which denotes the number of crystals per crystal length at any time t. The crystal growth rate G could be either dependent or independent of crystal size. Balancing the number of crystals in an infinitesimal interval of crystal length, a partial differential equation is obtained which explains the temporal evolution of CSD [12] [15]
 (1)
(1)
The corresponding initial and boundary conditions are given as
 (2)
(2)
The symbol T denotes temperature,  signifies the nucleation rate of particles at minimum crystal size
signifies the nucleation rate of particles at minimum crystal size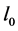 ,
,  is the maximum crystal size, and
is the maximum crystal size, and  is a Dirac Delta function. The solute concentration in the solution obeys the mass balance
is a Dirac Delta function. The solute concentration in the solution obeys the mass balance
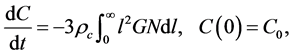 (3)
(3)
where  denotes the density of crystals. The negative sign on the right hand side of Equation (3) explains the decrease of solute concentration (mass) in the solution during the process of crystallization. The rate of nucleation of nuclei of size
denotes the density of crystals. The negative sign on the right hand side of Equation (3) explains the decrease of solute concentration (mass) in the solution during the process of crystallization. The rate of nucleation of nuclei of size  is expressed as
is expressed as
 (4)
(4)
where,  and b are regarded as kinetic parameters, V is the total crystals volume in the system, and
and b are regarded as kinetic parameters, V is the total crystals volume in the system, and  describes the saturated solute concentration which is depending on temperature of the solution. The crystal growth depending linearly on size may be defined as
describes the saturated solute concentration which is depending on temperature of the solution. The crystal growth depending linearly on size may be defined as
 (5)
(5)
In the above equation  is growth rate constant. The exponent
is growth rate constant. The exponent  is a kinetic parameter and a1 and a2 are constants. The relative super saturation
is a kinetic parameter and a1 and a2 are constants. The relative super saturation , which is a driving force for the crystallization process, is expressed as
, which is a driving force for the crystallization process, is expressed as
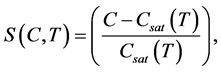 (6)
(6)
where  depends on the temperature T of the solution. A quadratic fit to the solubility data gives us
depends on the temperature T of the solution. A quadratic fit to the solubility data gives us
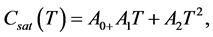 (7)
(7)
where, 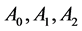 are regarded as constant parameters. Normally, temperature T is either considered constant (isothermal case) or a monotonically decreasing function of time (non-isothermal case). Hence
are regarded as constant parameters. Normally, temperature T is either considered constant (isothermal case) or a monotonically decreasing function of time (non-isothermal case). Hence 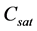 either remains constant or decreases with respect to time but remains positive.
either remains constant or decreases with respect to time but remains positive.
3. The Method of Characteristics
To avoid undesirable phenomena of primary nucleation which often adversely influence the crystal size distribution, seeded batches are operated in industrial batch crystallization. The secondary nucleation only produces infinitesimally small crystals in seeded batch runs. Since nuclei are produced at the minimum crystal size, we can consider a homogeneous PBE by defining the ratio of nucleation and growth terms as a left boundary condition:
 (8)
(8)
Note that Equation (8) is a hyperbolic partial differential equation due to the convection term (second term on the left hand side) and is equivalent to the Equation (1).
Before applying the numerical scheme, we discretize the computational domain. As explained before, the domain of interest is the crystal length, denoted by l. Suppose M is a large integer, and let  signifies the uniform partitioning of the given domain
signifies the uniform partitioning of the given domain . For
. For 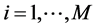 and interval length
and interval length
 , Ni indicate the average value of the number density in each cell
, Ni indicate the average value of the number density in each cell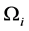 , i.e.
, i.e.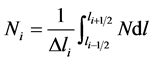 .
.
The rate of change by growth of the total number of particles in the i-th size range can be obtained by integrating Equation (8) with respect to l.
 (9)
(9)
By substituting the growth rate  in the above equation, we obtain
in the above equation, we obtain
 (10)
(10)
This gives
 (11)
(11)
The application of Leibnitz formula for differentiation of integral expressions that have variable limits of integration, Equation (11) becomes.
 (12)
(12)
This leads to the following semi-discrete equation:
 (13)
(13)
According the product rule, the above equation further simplifies to
 (14)
(14)
Thus, we get
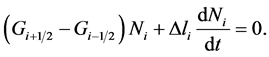 (15)
(15)
After simplifying the above equation, it takes the form
 (16)
(16)
Moreover, as described above
 (17)
(17)
Any time-discretization scheme can be used to solve jointly the system in Equations (16) and (17). In our case, a simple Euler method is employed. In Equations (16) and (17), there is no convection term which could cause much numerical error and instability. Hence the solution obtained by the MOC is very accurate and stable. To overcome the nucleation problem, a new mesh of the nuclei size is added at given time levels. The system size can be kept constant by deleting the last mesh at the same time levels. As a result, all variables ( and
and ) are reinitialized at these time levels and the time integrator restarts.
) are reinitialized at these time levels and the time integrator restarts.
4. Numerical Test Problems
In this section, some test problems are presented for the validation of the proposed numerical schemes. The results of MOC are compared with analytical solutions and results of the finite volume scheme presented in Qamar et al. [12] .
4.1. Test Problem 1
This test problem is taken from the article of Leonard et al. [16] with slight modifications. The growth rate is taken to be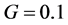 . The initial CSD is given as
. The initial CSD is given as
 (18)
(18)
Equation (18) corresponds to four characteristics peaks in the initial crystal size distribution. The first expression on the right side is a narrow Gaussian, the second and third expressions represent a square step and the last expression signifies a semi-ellipse. The last expression is very challenging because it combines sudden and gradual changes in the gradient. The analytic solution of this problem for the initial profile  is the initial profile which is translated by a distance
is the initial profile which is translated by a distance  i.e.
i.e.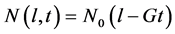 . We divide the crystal length
. We divide the crystal length  into 100 equal subintervals. Figure 1 compares the results of characteristic method, finite volume schemes and the analytical (exact) solution. It can be seen that MOC performed very well in resolving the sharp discontinuities of the step function and peak resolution of the Gaussian function. The MOC solution is comparable with the analytical solution and is superior over the solutions of finite volume schemes [12] .
into 100 equal subintervals. Figure 1 compares the results of characteristic method, finite volume schemes and the analytical (exact) solution. It can be seen that MOC performed very well in resolving the sharp discontinuities of the step function and peak resolution of the Gaussian function. The MOC solution is comparable with the analytical solution and is superior over the solutions of finite volume schemes [12] .
4.2. Test Problem 2
Lim et al. [17] considered this problem for analyzing their numerical algorithm. Here, the PBE in Equation (1) with nucleation and growth terms is considered. The growth rate is constant and the nucleation rate is independent of the solute concentration and, hence, Equation (3) is not needed. Assume that the stiff nucleation occurs at the minimum crystal size  as a function of time:
as a function of time:
 (19)
(19)
The crystal size and time ranges are considered as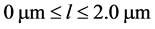 ,
,  , and
, and . The square step initial condition for the number density is expressed as:
. The square step initial condition for the number density is expressed as:
 (20)
(20)
The analytical solution is given as [6]
 (21)
(21)
Figure 2 illustrates the results. The numerical solutions are denoted by the symbol sign, whereas solid line shows the analytical solution. In the solution, a square step discontinuous shock and a narrow wave which is originated from nucleation moving along the propagation path line, . This problem is comparably harder than previous problems due to the stiff nucleation at the left boundary which produces a sharp peak and a profile. The numerical test is carried out on 200 grid points. It is evident that MOC resolves all the profiles of the solution in a better way than second order finite volume scheme [13] .
. This problem is comparably harder than previous problems due to the stiff nucleation at the left boundary which produces a sharp peak and a profile. The numerical test is carried out on 200 grid points. It is evident that MOC resolves all the profiles of the solution in a better way than second order finite volume scheme [13] .
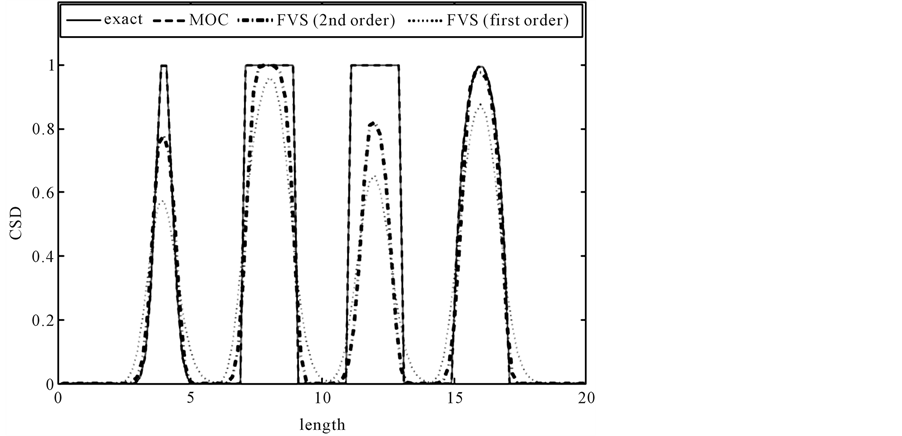
Figure 1. The result of test problem 1 for t = 1.
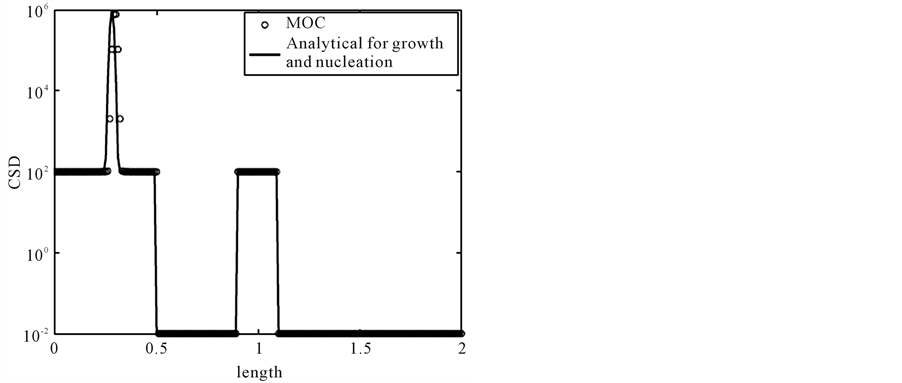

Figure 2. The result of test problem 2 at t = 0.5.
4.3. Test Problem 3
This test problem is taken from [9] which corresponds to the crystallization of potassium nitrate (KNO3) crystals. The nucleation rate is a function of the time-dependent concentration and growth rate is a function of both concentration and crystal size. Thus, we have to solve the coupled Equations (1)-(3). The initial size distribution is given as.
 (22)
(22)
Here we consider the crystals have volume . The initial condition for Equation (3) is taken as
. The initial condition for Equation (3) is taken as
 Also, mesh size is taken as
Also, mesh size is taken as . The given domain
. The given domain  is descritzed into 2200 cells and the simulation time is 1000 s. For size dependent growth rate, we consider
is descritzed into 2200 cells and the simulation time is 1000 s. For size dependent growth rate, we consider  and
and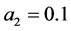 . Moreover, the values of constants in saturated concentration Equation (7) is taken as
. Moreover, the values of constants in saturated concentration Equation (7) is taken as ,
, 
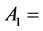 ,
, 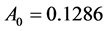 and the remaining parameters are given in Table1 Furthermore, the temperature trajectory is given as:
and the remaining parameters are given in Table1 Furthermore, the temperature trajectory is given as:
 (23)
(23)
No analytical solution exists in this case, thus the results of MOC and finite volume scheme are compared with each other. Figure 3 shows the final crystal size distributions (CSDs). It can be clearly seen that MOC resolves the steep gradients in nucleation part much better than the second order finite volume scheme [12] . The zoomed plots in Figure 4 clearly indicate that MOC is superior over the finite volume scheme.
4.4. Test Problem 4
The purpose of this test problem is to illustrate the applicability MOC for the case of discontinuous crystal growth rate. Here, the simulation of potassium sulfate (K2SO4∙H2O) is considered. The initial seed distribution is taken as [17] [18]
 (24)
(24)
The size range of interest is  and the final simulation time is 180 minutes. The growth rate, that replaces Equation (5), is described as
and the final simulation time is 180 minutes. The growth rate, that replaces Equation (5), is described as

Table 1 . Parametric value for test problem 3.


Figure 4. Zoomed plots of the results in test problem 3.
 (25)
(25)
where,  is the universal gas constant and
is the universal gas constant and 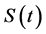 is given by Equation (6). The nucleation rate, that replaces Equation (4), is given as
is given by Equation (6). The nucleation rate, that replaces Equation (4), is given as
 (26)
(26)
Here,  is given as
is given as
 , (27)
, (27)
and 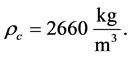 The volume shape factor is defined as
The volume shape factor is defined as
 (28)
(28)
The saturated concentration quantifying solute mass per gram of solvent is given as
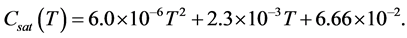 (29)
(29)
The temperature profile used to maintain a constant supersaturation  is given as
is given as
 (30)
(30)
The concentration balance in Equation (3) is replaced by the following equation
 (31)
(31)
The numerical results at 400 grid points are shown in Figure 5. It can be seen that MOC gives better approximation of the solution and correct positions of the discontinuities as compared to the finite volume scheme

Figure 5. The results of test problem 4.
[12] . Thus, MOC has better capability to solve such problems.
5. Conclusion
This work focused on the application of the method of characteristics (MOC) for solving batch crystallization models. The growth and nucleation were considered to be the dominant phenomena and breakage and nucleation were neglected. Three test problems were considered for different growth and nucleation rates. The performance and accuracy of the MOC was analyzed against the analytical solutions and the numerical solutions of finite volume schemes. Steep moving fronts or discontinuities appearing in the solutions were well captured by the MOC without any spurious oscillations and its results were found to be superior over the finite scheme results. It is therefore concluded that attention must be paid to the discretization of growth term (convection term) when devising a numerical algorithm. This could help to obtain a crystal size distribution which agrees well with the experimental one.