Set-Valued Stochastic Integrals with Respect to Finite Variation Processes ()
1. Introduction
Recently, integrals for set-valued stochastic processes with respect to Brownian motion, martingales and the Lebesgue measure have received much attention.
In 1997, Kisielewicz ([1]) defined the integral of setvalued process as a subset of  space, but he didn’t consider the measurability of the integral. In 1999, Kim and Kim [2] used the definition of stochastic integrals of set-valued stochastic process with respect to the Brownian motion. They called it Aumann ([3]) type It
space, but he didn’t consider the measurability of the integral. In 1999, Kim and Kim [2] used the definition of stochastic integrals of set-valued stochastic process with respect to the Brownian motion. They called it Aumann ([3]) type It integrals. In [4], Jung and Kim modified the definition by taking the decomposable closure such that the integral is measurable. Li and Ren [5] modified Jung and Kim’s definition by considering the predictable set-valued stochastic process as a set-valued random variable in the product space
integrals. In [4], Jung and Kim modified the definition by taking the decomposable closure such that the integral is measurable. Li and Ren [5] modified Jung and Kim’s definition by considering the predictable set-valued stochastic process as a set-valued random variable in the product space , and the measurability and decomposability also were based on product
, and the measurability and decomposability also were based on product  -algebra. After that, Zhang et al. ([6,7]) studied the set-valued integrals with respect to the martingale and Brownian motion.
-algebra. After that, Zhang et al. ([6,7]) studied the set-valued integrals with respect to the martingale and Brownian motion.
Stochastic differential inclusions and set-valued stochastic differential (or integral) equations are employed to model the problems with not only randomness but also impreciseness. Recently, there are some references related to set-valued differential equations such as [8-13] etc.
Concerning to the integral with respect to finite variation processes, Malinowski and Michta [12] give the notion of set-valued integral with respect to single valued finite variation but without considering the measurability. Z.Wang and R.Wang [14] defined the Lebesgue-Stieltjes stochastic integral of single valued stochastic processes with respect to set-valued finite variation processes (refer to [14] for the detail).
In this paper, different from the definition in [14], based on the Definition 3.1 in [12], we will study the Lebesgue-Stieltjes integral of set-valued stochastic processes with respect to single valued finite variation process. We shall prove the measurability of integral, namely, it is a set-valued random, which is similar to the classical stochastic integral.
This paper is organized as follows: in section 2, we present some notions and facts on set-valued random variables; in section 3, we shall give the definition of integral of set-valued stochastic processes with respect to finite variation process and then prove the measurability and  -boundedness.
-boundedness.
2. Preliminaries
We denote  the set of all natural numbers,
the set of all natural numbers,  the set of all real numbers,
the set of all real numbers,  the d-dimensional Euclidean space with the usual norm
the d-dimensional Euclidean space with the usual norm ,
,  the set of all nonnegative numbers. Let
the set of all nonnegative numbers. Let  be a complete probability space,
be a complete probability space,  a
a  -field filtration satisfying the usual conditions. Let
-field filtration satisfying the usual conditions. Let  be a Borel field of a topological space
be a Borel field of a topological space .
.
Let  (resp.
(resp. ) be the family of all nonempty, closed (resp. nonempty compact, nonempty compact convex) subsets of
) be the family of all nonempty, closed (resp. nonempty compact, nonempty compact convex) subsets of . For any
. For any  and
and , define the distance between
, define the distance between  and A by
and A by . The Hausdorff metric
. The Hausdorff metric  on
on  (see e.g. [15]) is defined by
(see e.g. [15]) is defined by
 (1)
(1)
 .
.
Denote . For
. For  , we have
, we have

For  the support function of
the support function of  is defined as follows:
is defined as follows:

 : the set of all
: the set of all —valued Borel measurable functions
—valued Borel measurable functions  such that the norm
such that the norm

is finite.  is called
is called 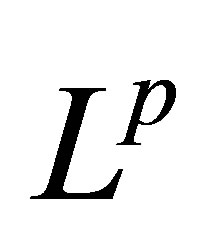 -integrable if
-integrable if .
.
A set-valued function  is said to be measurable if for any open set
is said to be measurable if for any open set , the inverse
, the inverse  belongs to
belongs to . Such a function
. Such a function  is called a set-valued random variable.
is called a set-valued random variable.
Let  (resp.
(resp. ,
, ) be the family of all measurable
) be the family of all measurable  -valued (resp.
-valued (resp.  -valued) functions, briefly by
-valued) functions, briefly by  (resp.
(resp.  ,
, . For
. For , the family of all
, the family of all  -integrable selections is defined by
-integrable selections is defined by
 (2)
(2)
In the following,  is denoted briefly by
is denoted briefly by .
.
A set-valued random variable  is said to be integrable if
is said to be integrable if 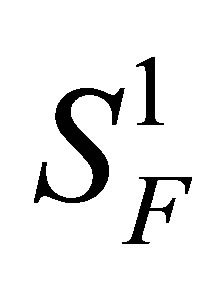 is nonempty.
is nonempty.  is called
is called  -integrably bounded if there exits
-integrably bounded if there exits  s.t. for all
s.t. for all ,
,  almost surely.
almost surely.
An  -valued stochastic process
-valued stochastic process  (or denoted by
(or denoted by ) is defined as a function
) is defined as a function  with the
with the  -measurable section
-measurable section , for
, for . We say
. We say  is measurable if
is measurable if  is
is  - measurable. The process
- measurable. The process  is called
is called  -adapted if
-adapted if  is
is  -measurable for every
-measurable for every . Let
. Let , where
, where  . We know that
. We know that  is a
is a  -algebra on
-algebra on . A function
. A function  is measurable and
is measurable and  -adapted if and only if it is
-adapted if and only if it is  -measurable ([8]).
-measurable ([8]).
In a fashion similar to the  -valued stochastic processes, a set-valued stochastic process
-valued stochastic processes, a set-valued stochastic process  is defined as a set-valued function
is defined as a set-valued function  with
with  -measurable section
-measurable section  for
for . It is called measurable if it is
. It is called measurable if it is 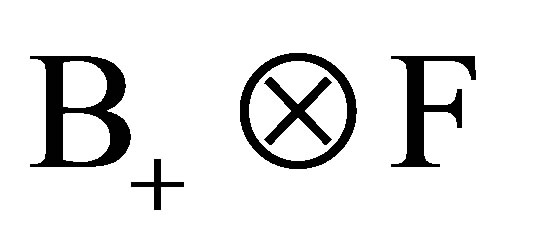 -measurable, and
-measurable, and  - adapted if for any fixed
- adapted if for any fixed ,
,  is
is  -measurable.
-measurable.  is measurable and
is measurable and  -adapted if and only if it is
-adapted if and only if it is  -measurable.
-measurable.  is called
is called  -integrable if every
-integrable if every  is
is  -integrable.
-integrable.
3. Set-Valued Stochastic Integral w.r.t Finite Variation Processes
Let  be a real valued
be a real valued  -adapted measurable process with finite variation and continuous sample trajectories a.s. from the origin. That is to say, for each compact interval
-adapted measurable process with finite variation and continuous sample trajectories a.s. from the origin. That is to say, for each compact interval  and any partition
and any partition  of
of , the total variation
, the total variation

is finite and  a.s. Then for any
a.s. Then for any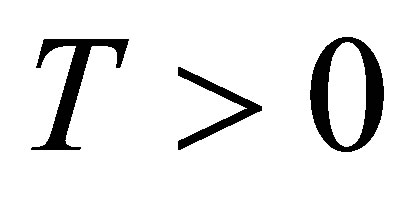 , the process
, the process  can generate a random measure denoted by
can generate a random measure denoted by  in the space
in the space . For any
. For any , let
, let

where  is the decomposition of
is the decomposition of ,
,  and
and  are non-negative and nondecreasing processes,
are non-negative and nondecreasing processes, . In the product space
. In the product space , set
, set
 (3)
(3)
for , where
, where  is the index function. Then the set function
is the index function. Then the set function  is a finite measure in the measurable space
is a finite measure in the measurable space  if and only if
if and only if  . In the following we always assume
. In the following we always assume .
.
Let  be the family of all
be the family of all  -measurable
-measurable  -valued stochastic processes
-valued stochastic processes  such that
such that

For any  and
and , the stochastic Lebesgue-Stieltjes integral
, the stochastic Lebesgue-Stieltjes integral  is defined by the Bochner integral
is defined by the Bochner integral  pathby-path. One can show that the integral process
pathby-path. One can show that the integral process
 is
is  -measurable.
-measurable.
Note: in [12], the integrand is assumed being predictable, in fact the integrand can be relaxed to the  - measurable class since the integrator
- measurable class since the integrator  is continuous.
is continuous.
Let  be the family of all
be the family of all 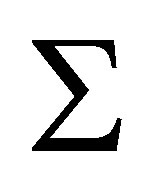 -measurable
-measurable  -valued stochastic processes
-valued stochastic processes  such that
such that

where . For any
. For any  , set
, set
 (4)
(4)
Definition 1. (see [12]) For a set-valued stochastic process  the set-valued stochastic Lebesgue-Stieltjes integral (over interval
the set-valued stochastic Lebesgue-Stieltjes integral (over interval ) of
) of  with respect to the finite variation continuous process
with respect to the finite variation continuous process  is the set
is the set

In [12], the authors call this kind of integral as trajectory integral since they consider it as a
 -valued random variable. Here, we shall consider it as a subset of
-valued random variable. Here, we shall consider it as a subset of  and show the measurability with respect to
and show the measurability with respect to , which is very different from the way in [12], also different from other references such as [10,16,17] etc. In fact, for almost every
, which is very different from the way in [12], also different from other references such as [10,16,17] etc. In fact, for almost every , the above integral
, the above integral  is a subset of
is a subset of . In the following, we shall assume the
. In the following, we shall assume the  - algebra
- algebra  is separable w.r.t
is separable w.r.t . In addition,
. In addition,  is separable and
is separable and , then one can get
, then one can get  is separable. Therefore we can find an
is separable. Therefore we can find an  - measurable set
- measurable set , such that
, such that  and for every
and for every
 , the integral
, the integral  is defined path-bypath. For
is defined path-bypath. For , set
, set , therefore it is well defined for every
, therefore it is well defined for every .
.
 since the continuity of
since the continuity of
 . In the sequel, we shall denote the integral by
. In the sequel, we shall denote the integral by
 instead of
instead of . For any
. For any denote
denote  by
by .
.
Theorem 1. For ,
,  and
and , the Lebesgue-Stieltjes integral
, the Lebesgue-Stieltjes integral  is a compact and convex subset of
is a compact and convex subset of .
.
Proof 1. In fact,  is a bounded and convex subset of
is a bounded and convex subset of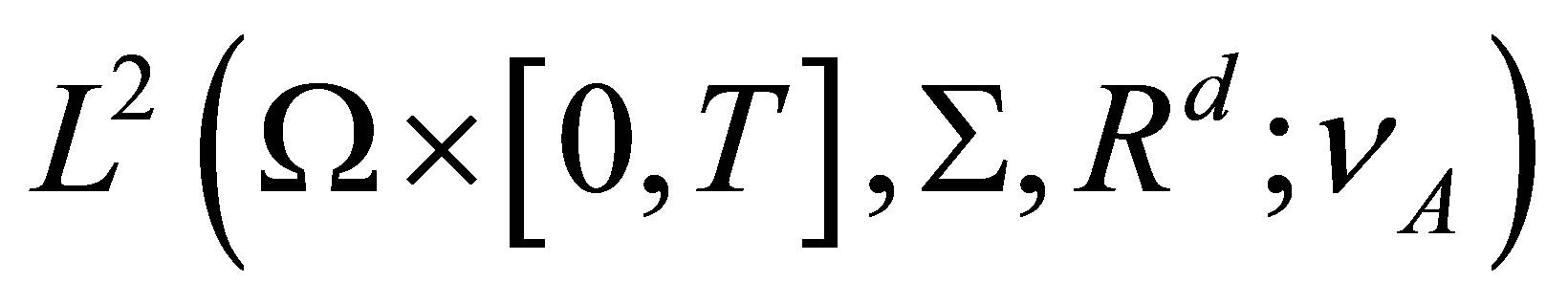 , since
, since  is convex and compact,moreover, it is weakly compact since
is convex and compact,moreover, it is weakly compact since  is reflexive. The convexity of the integral is obvious.
is reflexive. The convexity of the integral is obvious.
We shall show the linear operator  :
:  is bounded.
is bounded.
For any ,
,  ,
,
 (5)
(5)
which implies the linear operator  is bounded. Therefore the integral
is bounded. Therefore the integral  is weakly compact since the bounded linear operator mapping a weakly compact set to a weakly compact one. In
is weakly compact since the bounded linear operator mapping a weakly compact set to a weakly compact one. In  space, a weakly compact set is compact.
space, a weakly compact set is compact.
Lemma 1. (see [16] Corollary 2.1.1 (5)) Assume  is a measurable space,
is a measurable space,  is a separable Banach space,
is a separable Banach space,  , and F is a set-valued random variable, then
, and F is a set-valued random variable, then 
 is measurable.
is measurable.
By using Lemma 1, as a manner similar to Theorem 1 in [17], we have the following result:
Lemma 2. Assume  is the corresponding stochastic process,
is the corresponding stochastic process,  for any
for any , we have 1)
, we have 1) ;
;
2) 
Lemma 3. (see [16] Theorem 2.1.16) Assume  is a measurable space,
is a measurable space,  is a separable Banach space,
is a separable Banach space,  , and for any fixed
, and for any fixed 
 is measurable, if one of the following conditions is satisfied:
is measurable, if one of the following conditions is satisfied:
1)  is separable;
is separable;
2) for any .
.
Then  is a set-valued random variable.
is a set-valued random variable.
From Lemma 1 and Lemma 3, when , for any
, for any ,
, 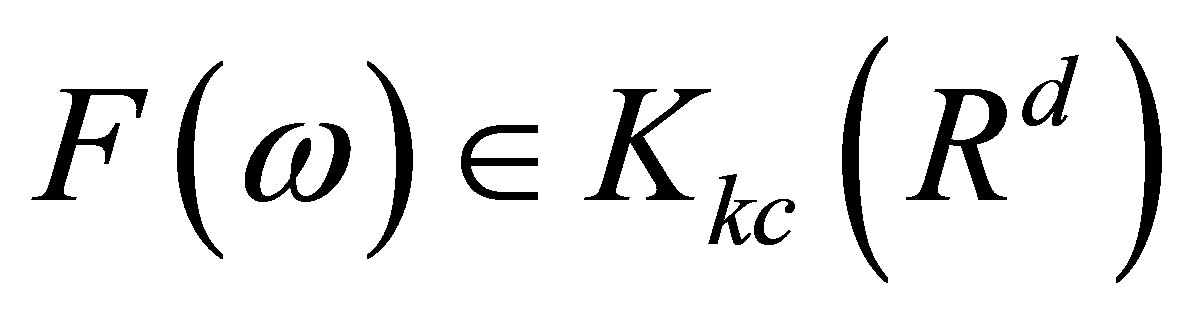 is
is  -measurable if and only if
-measurable if and only if  is
is 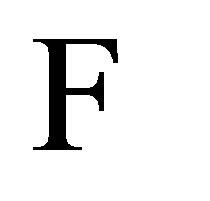 -measurable.
-measurable.
Lemma 4. ([16] Theorem 1.7.7) If  is a separable space,
is a separable space,  are separable metric space
are separable metric space  satisfy:
satisfy:
(a) for any  is measurable;
is measurable;
(b) for any  is continuous or is continuous with respect to Hausdorff metricThen
is continuous or is continuous with respect to Hausdorff metricThen  is jointly measurable.
is jointly measurable.
Then by Lemma 1 we have the following:
Lemma 5. Assume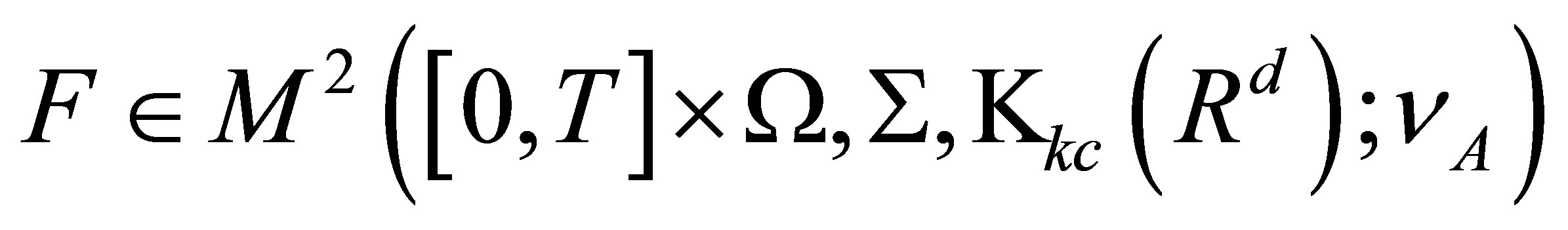 . Then
. Then  is
is  -measurable.
-measurable.
Theorem 2. Assume  . Then
. Then  for each
for each . Furthermore, the mapping
. Furthermore, the mapping  is
is  -measurable.
-measurable.
Proof 2. Step 1. We will show that  is
is  - measurable for each
- measurable for each ,
,  is
is  -measurable.
-measurable.
By Theorem 1, we have
 (6)
(6)
for all . Furthermore, we obtain
. Furthermore, we obtain

for all . Moreover, since
. Moreover, since  is
is  -measurable, from the Lemma 5 we can obtain that the function
-measurable, from the Lemma 5 we can obtain that the function  is
is  measurable. By Fubini theorem,
measurable. By Fubini theorem,  is
is  -measurable, based on Lemma 3,
-measurable, based on Lemma 3,  is
is  -measurable.
-measurable.
Finally, in the argument above, the function  is
is  -measurable for each
-measurable for each . Since it is continuous in
. Since it is continuous in  for all
for all , so it is
, so it is  -measurable. From Lemma 4, we obtain that
-measurable. From Lemma 4, we obtain that  is
is  - measurable.
- measurable.
Step 2. In this step, we will show that  for each
for each .
.
For each  and
and , we have
, we have
 (7)
(7)
then

Hence,
 (8)
(8)
which implies

As a manner similar to Theorem 3.8. in [8], we have the Castaing representation as following:
Theorem 3. For a set-valued stochastic process , there exists a sequence
, there exists a sequence  such that
such that

and, for ,
,

where cl denotes the closure in .
.
Theorem 4. For each 
 is continuous a.s. with respect to the Hausdorff metric
is continuous a.s. with respect to the Hausdorff metric .
.
Proof 3. Let  and
and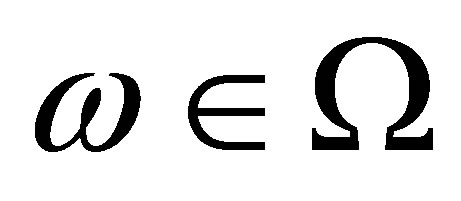 . We then have
. We then have
 (9)
(9)
Hence,

(10)
since for each ,
, . Hence,
. Hence, . So
. So  is leftcontinuous in
is leftcontinuous in  for all a.s. In a similar way, we see that
for all a.s. In a similar way, we see that  is right-continuous in
is right-continuous in  a.s.
a.s.
Similar to the proof of Theorem 3.15 in [8], we have the following theorem:
Theorem 5. Let , for any
, for any , we have
, we have

and

4. Conclusion
When the integrand takes values in compact and convex subsets of , we defined the integral with respect to real-valued variation processes. And then we proved some properties of this kind of integral such as measurability,
, we defined the integral with respect to real-valued variation processes. And then we proved some properties of this kind of integral such as measurability,  -boundedness and continuity under the Hausdorff metric.
-boundedness and continuity under the Hausdorff metric.
5. Acknowledgements
We would like to thank the referees for their valuable comments. Moreover, we express special thanks to our editor of the journal APM for his(her) efficiency and support.
NOTES
#Corresponding author.