Quantum Effects on the Rayleigh-Taylor Instability of Viscoelastic Plasma Model through a Porous Medium ()
1. Introduction
The Rayleigh-Taylor instability (RTI) is an important hydrodynamic effect that arises when a heavy fluid is accelerated into a lighter one. Similar to pouring water into oil, the heavier fluid, once perturbed, streams to the bottom, pushing the light fluid aside. This notion for a fluid in a gravitational field was first discovered by Rayleigh [1] and later applied to all accelerated fluids by Taylor [2]. Since then, this instability problem has been studied by several researchers under varying assumptions. The detailed description of other parameters of these investigations has been given by Chandrasekhar [3]. A theoretical model, for a class of viscoelastic fluids have been proposed by Oldroyd [4-6]. The Rayleigh-Taylor instability of a plane interfaces between viscous and viscoelastic fluid through a porous medium has been investigated by Sharma and Kumar [7]. Agrawal and Goel [8] have studied the instability of viscoelastic fluid in a porous medium. Bhatia and Mathur [9] have studied the instability of viscoelastic fluids in a vertical magnetic field through porous medium. Kumar et al. [10] have considered the instability of the plane interface between two viscoelastic superposed fluids in the presence of uniform rotation and variable magnetic field in porous medium.
In plasmas, RTI can occur when dense plasma is supported against gravity by the pressure of the magnetic field. The investigation of Rayleigh-Taylor instabilities in magnetized plasma is a problem of considerable interest in space (ionospheric spread-F), fusion (curvature induced instabilities like interchange, ballooning, etc.) and the astrophysical plasmas. For a system of two incompressible plasma superimposed one over the other have been studied by Kalra and Talwar [11] and by Singh and Tandon [12]. Bhatia [13] studied the problem for a system of superimposed viscous plasmas in the presence of a horizontal magnetic field. The same previous system in the presence of uniform rotation was considered by Bhatia and Chhonkar [14] and by Sharma and Chhajlani [15]. The effects of Hall currents and viscosity on the Rayleigh-Taylor instability of incompressible infinitely conducting stratified plasma in the presence of horizontal magnetic field were studied by Ahsan and Bhatia [16]. The effects of Hall currents on the RTI of finitely conducting stratified partially ionized plasma in the presence of horizontal magnetic field is considered by Aiyub and Bhatia [17].
The linear growth rate of a finite layer plasma in which the density is continuously stratified exponentially along the vertical is studied by Goldston and Rutherford [18], in the presence of horizontal magnetic and rotation was studied by Bhatia and Sharma [19] and in the presence of horizontal magnetic field with the effect of a transverse velocity shear was studied by Wu et al. [20]. The effects of external magnetic field on RTI problem in inhomogeneous plasma rotating uniformly is studied by Al-Khateeb and Laham [21,22]. The effect of the velocity shear-induced viscosity gradient of low-frequency shear waves in viscoelastic dusty plasma was studied by Banerjee et al. [23]. The gravitational instability of rotating Walters  viscoelastic partially ionized plasma permeated by an oblique magnetic field has been investigated in the presence of the effects of Hall currents by El-Sayed and Mohamed [24].
viscoelastic partially ionized plasma permeated by an oblique magnetic field has been investigated in the presence of the effects of Hall currents by El-Sayed and Mohamed [24].
The hydrodynamic instabilities in quantum plasmas have been an important subject of research in the last a few years, where the quantum effects plays an important role in the behavior of the charged plasma particles when the de Broglie wavelength of the charge carriers becomes equal to or greater than the dimension of the quantum plasma system [25]. The quantum hydro-dynamic (QHD) model has been introduced by Gardner [26] for semiconductor physics to describe the transport of charge, momentum and energy in plasmas. The quantum magneto-hydrodynamic (QMHD) model was obtained by Haas [27] with the help of QHD model with magnetic field based on the Wigner-Maxwell equations. The Influence of quantum mechanism on the internal waves and the RTI in plasma is considered by Bychkov et al. [28]. The effects of the quantum mechanism and magnetic field on RTI in ideal incompressible plasma are studied by Jintao et al. [29], where it plays a stability role on this problem. Quantum effects on RTI in inhomogeneous plasma rotating uniformly in an external magnetic field are investigated by Hoshoudy [30,31]. The effects of magnetic field on the RTI in quantum plasmas with paraand ferromagnetic properties have been considered by Mikhail et al. [32].The effect of quantum term on RTI of stratified plasma layer through porous medium is studied by Hoshoudy [33]. The RTI is investigated in a non-uniform dense quantum magneto-plasma by Ali et al. [34].
The purpose of this work is to examine theoretically the effect of the quantum mechanism on RTI for a finite thickness layer of incompressible viscoelastic plasma through porous media. This layer is confined between two rigid boundaries (
 ). Using the normal mode approach, the dispersion relation is obtained analytically, and numerically analyzed.
). Using the normal mode approach, the dispersion relation is obtained analytically, and numerically analyzed.
2. Fundamental Equations
Our starting point is the set of equations of the quantum hydrodynamic (QHD) for an plasma model through a porous media (4-10 and 27-34).
 (1)
(1)
 (2)
(2)
Here 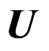 is the velocity of the fluid,
is the velocity of the fluid,  is the density,
is the density,  thermal pressure,
thermal pressure, 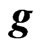 is the gravitational acceleration,
is the gravitational acceleration,  is permeability of the medium and
is permeability of the medium and 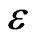 is the porosity (
is the porosity ( ). Note that when
). Note that when  and
and  the system corresponds to a nonporous medium.
the system corresponds to a nonporous medium. 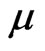 is the viscosity of plasma. Here
is the viscosity of plasma. Here 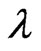 is the stress relaxation time,
is the stress relaxation time,  is the strain retardation time.
is the strain retardation time.
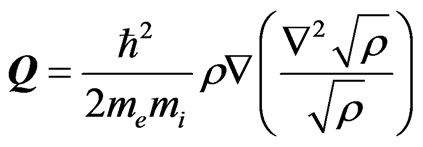 is represented by Bohm Potential term (also, is called a quantum pressure and for more details on the derivation, see refs. [27,35]), where
is represented by Bohm Potential term (also, is called a quantum pressure and for more details on the derivation, see refs. [27,35]), where  is the Plank constant,
is the Plank constant,  is the electron mass and
is the electron mass and  the ion mass.
the ion mass.
To investigate the stability of hydrodynamic motion, we ask how the motion responds to a small fluctuation in the value of any of the flow variables appearing in the Euler equations. If the fluctuation grows in amplitude so that the flow never returns to its initial state, we say that the flow is unstable with respect to fluctuations of that type. Accordingly, we replace the variables in Equations (1) and (2) as in the form 

 and
and . The quantities with subscripts “0” represent the unperturbed, or “zeroth-order” motion of the fluid, while the quantities with subscripts “1” represent a small perturbation about the zeroth-order quantities (first-order or linearized quantities); that is,
. The quantities with subscripts “0” represent the unperturbed, or “zeroth-order” motion of the fluid, while the quantities with subscripts “1” represent a small perturbation about the zeroth-order quantities (first-order or linearized quantities); that is, 

 and
and  Substituting these expressions into Equations (1)-(4). In particular example of RTI we consider the fluid initially at rest. This means that
Substituting these expressions into Equations (1)-(4). In particular example of RTI we consider the fluid initially at rest. This means that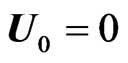 , so the linearized equations can be easily derived from Equations (1) and (2) as
, so the linearized equations can be easily derived from Equations (1) and (2) as
 (3)
(3)
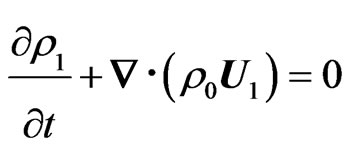 (4)
(4)
 (5)
(5)
We now appeal to the fact that, for many situations of interest in ICF (inertial-confinement fusion), unstable flow occurs at velocities much smaller than the local sound speed. This has the effect that accelerations in the flow are not strong enough to change the density of a fluid element significantly, so the fluid moves without compressing or expanding. In such a situation we call the flow incompressible. Provided that we are well away from shock waves or centers of convergence, the assumption of incompressible flow is often valid. To say that fluid elements move without changing density is to say that the Lagrangian total derivative of density is zero, that
 (6)
(6)
We also linearize this equation, where the first-order quantities, as before become
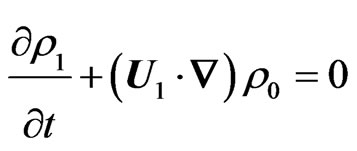 (7)
(7)
Comparing this equation to Equation(4), which can be rewritten in expanded form as
 (8)
(8)
we see that subtracting Equation (7) from Equation (8) yields
 (9)
(9)
This is a consequence of the assumption of incompressible flow. So, we can use either Equation (7) or Equation (9) to replace the linearized continuity Equation (4) under this assumption. One can seen that the set of Equations (3), (7) and (9) is complete for describing the quantum effects on the Rayleigh-Taylor instability of incompressible plasma. Now, where
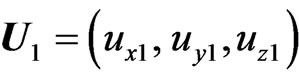 ,
, 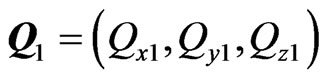
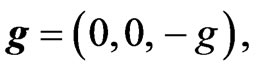
The fluid is arranged in horizontal strata, and then  is a function of the vertical coordinate
is a function of the vertical coordinate and
and .Then, the system Equations (3), (7) and (9) become as in the appendix (Equations (30)-(37)).
.Then, the system Equations (3), (7) and (9) become as in the appendix (Equations (30)-(37)).
Considering that the perturbation in any physical quantity takes the form
 (10)
(10)
where  and
and  are horizontal components of the wave-number vector
are horizontal components of the wave-number vector  such that
such that  and
and  (may be complex (
(may be complex ( )) is the frequency of perturbations or the rate at which the system departs from equilibrium thee initial state. Using the expression (10) in the system of equations (30)-(37) in the appendix, they become as in the appendix (see Equations (38)-(45))
)) is the frequency of perturbations or the rate at which the system departs from equilibrium thee initial state. Using the expression (10) in the system of equations (30)-(37) in the appendix, they become as in the appendix (see Equations (38)-(45))
Now, eliminating some of the variables from the system of Equations (38)-(42) in the appendix, we have
 (11)
(11)
and if we consider,
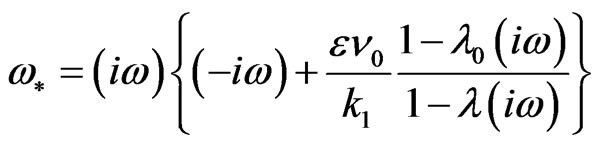 (12)
(12)
Then Equation (11) becomes
 (13)
(13)
where
 (14)
(14)
3. A Continuously Stratified Plasma Layer
For a finite thickness layer of incompressible plasma through porous media bounded on the other interface by a rigid boundary at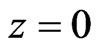 ,
,  and
and , Equation (13) takes the form
, Equation (13) takes the form
 (15)
(15)
where .
.
Now, we put the solution of Equation (15) in the form
 and substituting into Equation
and substituting into Equation
(15), the dispersion relation may be written as
 (16)
(16)
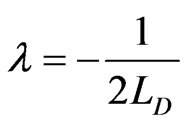
Now, we insert the following dimensionless quantities in Equation (16)


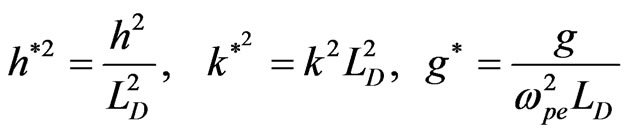
where 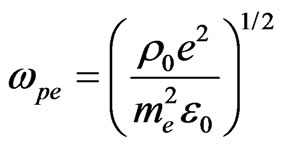 is the plasma frequency, and use Equation (12), then the dispersion relation (16) takes the form
is the plasma frequency, and use Equation (12), then the dispersion relation (16) takes the form
 (17)
(17)
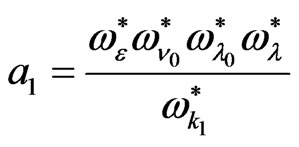 (18)
(18)
 (19)
(19)
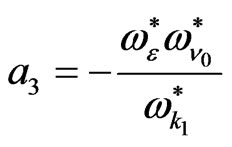 (20)
(20)
 (21)
(21)
From the system of Equations (17)-(21), it is clear that, the effect of strain retardation time  is connected by the presence of the resistance term (i.e., the effect of
is connected by the presence of the resistance term (i.e., the effect of  will occur in the presence of
will occur in the presence of ), while the effect of stress relaxation time
), while the effect of stress relaxation time  may be occur alone or it is connected by the presence of
may be occur alone or it is connected by the presence of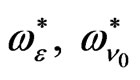 ,
,  and
and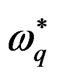 .
.
Now, where 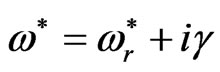 and in the case of
and in the case of  and
and 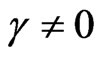 (stable oscillations), then Equation (17) becomes
(stable oscillations), then Equation (17) becomes
 (22)
(22)
4. Special Cases
Here, some special cases are considered from Equation (22) to clarify the different roles of the parameter’s problem.
1) At , we find that
, we find that ,
, and
and
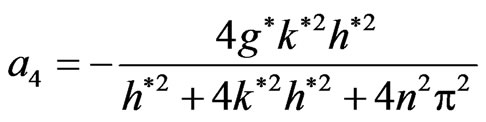
So the normalized growth rate from Equation (22) is
 (23)
(23)
This case is considered by Goldston and Rutherford (see ref. [18]), where the system represents an exponentially growing perturbation.
2) At , we find that
, we find that ,
, 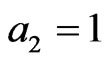 , while
, while  is as in Equation (21). So the normalized growth rate from Equation (22) is
is as in Equation (21). So the normalized growth rate from Equation (22) is
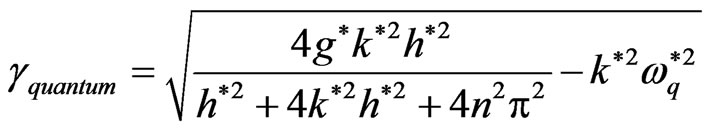 (24)
(24)
This case is studied in Refs. [29-33]. It is clarified that, the quantum term has stabilizing effect on RTI problem. This influence is obvious from Equations (23) and (24), where  for all the values of wave number. Also, the system increases as
for all the values of wave number. Also, the system increases as  increases through the range
increases through the range , when
, when 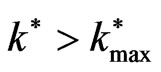 it starts to decreases as
it starts to decreases as increases, where
increases, where
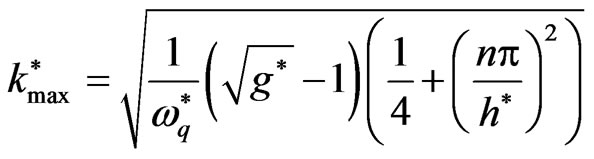
and at 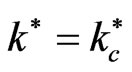 the system arrives to complete stability with
the system arrives to complete stability with 
3) At  we find that
we find that , while
, while

and
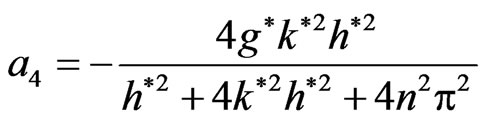
Then the normalized growth rate from Equation (22) is given by
 (25)
(25)
Also, from Equations (23) and (25) one can see that, the stress relaxation time has a stabilizing role on the given system. This role increases with increasing of the magnitudes of stress relaxation time. While in the presence of quantum term the normalized growth rate in Equation (25) takes the form
 (26)
(26)
from above results it very clear that

4) At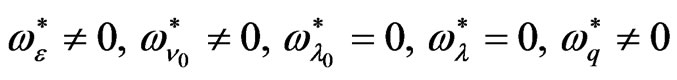 , we find that
, we find that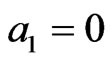 ,
,  , while
, while 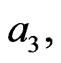
 are as in Equations (20) and (21). So the normalized growth rate given by
are as in Equations (20) and (21). So the normalized growth rate given by
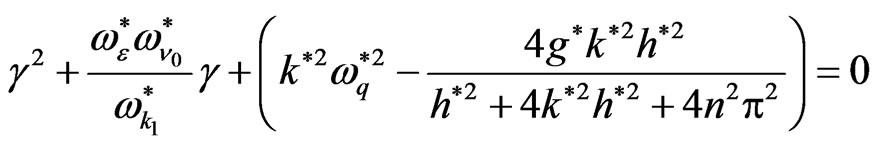 (27)
(27)
corresponds Equation (33) ref. [33], where the normalized growth rate given by
 (28)
(28)
and in the presence of the strain retardation, Equation(28) becomes
 (29)
(29)
From Equations (28) and (29) one can see that, the stabilizing role that plays the stress strain retardation time on the given system.
In the general case, if we wish to look into the effect of various factors, on the instability of the considered system, Equation (22) is to be numerically solved. Pertaining results are presented in Figures 1-3.
Figure 1 shows the effect of the factors 
 and
and  every one is alone, where the square normalized growth rate
every one is alone, where the square normalized growth rate is plotted against the square normalized wave number
is plotted against the square normalized wave number . One can see that, in the absence of
. One can see that, in the absence of  the magnitudes of
the magnitudes of  in the presence of the factors
in the presence of the factors 

 and
and  are less than their magnitudes in the classical case, which means that these factors have a stabilizing effect on the considered system. Also, it can be seen that, no mode of maximum instability exists when
are less than their magnitudes in the classical case, which means that these factors have a stabilizing effect on the considered system. Also, it can be seen that, no mode of maximum instability exists when  as the square normalized growth rate
as the square normalized growth rate  usually increases by increase with the square normalized wave number values. While, in the presence of quantum term
usually increases by increase with the square normalized wave number values. While, in the presence of quantum term 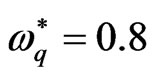 (the detailed description of this case is given in the next part), there is a mode of maximum instability, where the square normalized growth rate
(the detailed description of this case is given in the next part), there is a mode of maximum instability, where the square normalized growth rate  increases with
increases with  increases through the range
increases through the range  (at
(at  the square normalized growth rate arrives to the maxi-
the square normalized growth rate arrives to the maxi-
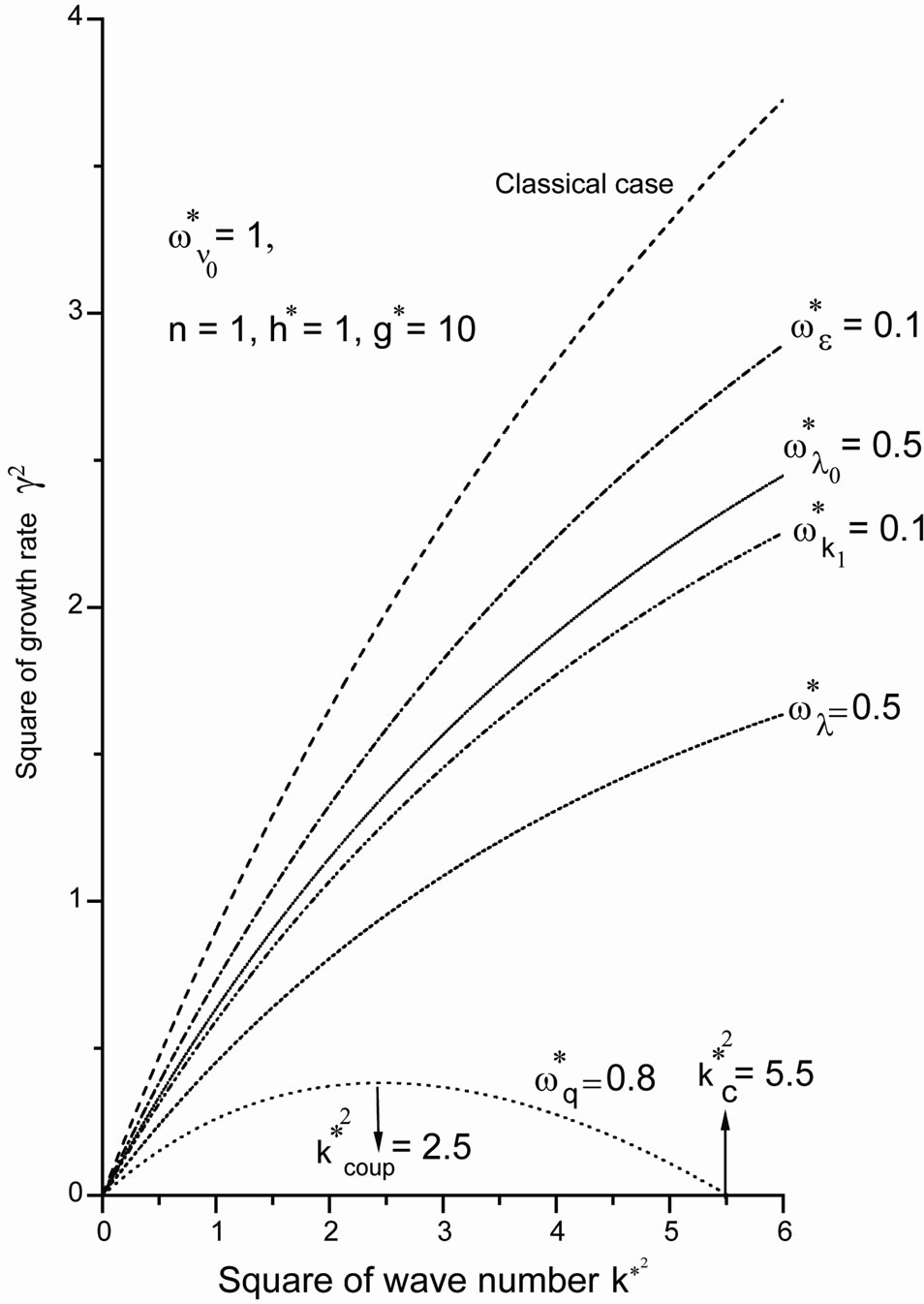
Figure 1. The square normalized growth rate γ2 against the square normalized wave number , where the role of the different parameters are separated occurred at n = 1, h* = 1 and g* = 10.
, where the role of the different parameters are separated occurred at n = 1, h* = 1 and g* = 10.
mum instability, for our example in Figure 1 and at 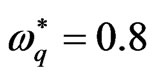 we note
we note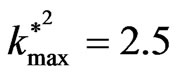 ), and when
), and when 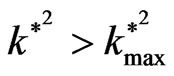 the square normalized growth rate
the square normalized growth rate 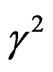 starts to decreases as
starts to decreases as  increases and then goes to the complete stable at
increases and then goes to the complete stable at  (
( is the critical value for stability, at this point the square normalized growth rate goes to zero). This means that the quantum term has a crucial capability to suppress the instability, while the other factors have not liked this strength.
is the critical value for stability, at this point the square normalized growth rate goes to zero). This means that the quantum term has a crucial capability to suppress the instability, while the other factors have not liked this strength.
The role of porosity of the porous medium, the medium permeability, kinematic viscosity with quantum term is explained in ref. [33]. So, our next numerical results concentrate on the role of both strain retardation and stress relaxation.
Figures 2 and 3 are plotted to indicate the influence of the strain retardation time  and the stress relaxation time
and the stress relaxation time  on the problem, respectively, in the presence of quantum effect
on the problem, respectively, in the presence of quantum effect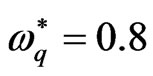 . Figure 2 shows that the presence of
. Figure 2 shows that the presence of  does not effect on both the maximum point
does not effect on both the maximum point  for the instability and the corresponding critical point
for the instability and the corresponding critical point for the stability, where
for the stability, where  and
and 
at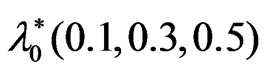 . The same note for the stress relaxation time
. The same note for the stress relaxation time  is shown in Figure 3. However, the magnitudes of
is shown in Figure 3. However, the magnitudes of 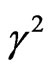 in the presence of both
in the presence of both 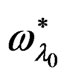 and
and  are less than their magnitudes in the presence of the quantum term alone, which implies that both
are less than their magnitudes in the presence of the quantum term alone, which implies that both  and
and  have a stabilizing role on the considered system. For the same values, the effect of the stress relaxation time
have a stabilizing role on the considered system. For the same values, the effect of the stress relaxation time 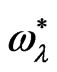 is greater than the effect of the strain retardation time
is greater than the effect of the strain retardation time  on the considered system.
on the considered system.
5. Conclusions
The effect of quantum term on the Rayleigh-Taylor instability of stratified fluid/plasma through porous media has been studied. The effect of elasticity is revealed through the strain retardation time and the stress relaxation time. It is found that, the critical point for the stability
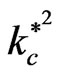 that occurs in the presence of quantum term remains unchanged by the addition of the other parameters of the problem. Both maximum
that occurs in the presence of quantum term remains unchanged by the addition of the other parameters of the problem. Both maximum  and critical
and critical  point for the instability are unchanged by the addition of the strain retardation and the stress relaxation. All growth rates are reduced in the presence of porosity of the medium, the medium permeability, the strain retardation time and the stress relaxation time. These results indicate that quantum effect plays a major role in securing a complete stability for the system at hand, while other parameters are only of secondary significance.
point for the instability are unchanged by the addition of the strain retardation and the stress relaxation. All growth rates are reduced in the presence of porosity of the medium, the medium permeability, the strain retardation time and the stress relaxation time. These results indicate that quantum effect plays a major role in securing a complete stability for the system at hand, while other parameters are only of secondary significance.
Finally, our select model is more stable than those considered in refs. [29-33]. This discrepancy highlights a stabilizing role due to the presence of both the strain retardation and the stress relaxation on Rayleigh-Taylor instability problem, increasing the dissipation of any disturbance, thus providing an increased stability.
6. Acknowledgements
The author would like to thank the referees for their useful suggestions and comments that improved the original manuscript.
Appendix
Here, if we put
 ,
,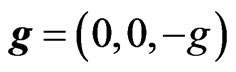 ,
, 
and
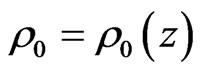
Then, the system Equations (3), (7) and (9) maybe written as
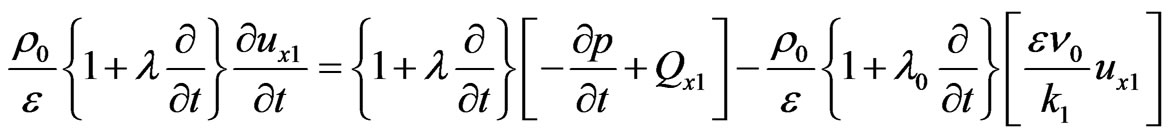 (30)
(30)
 (31)
(31)
 (32)
(32)
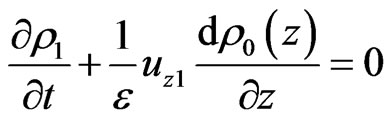 (33)
(33)
 (34)
(34)
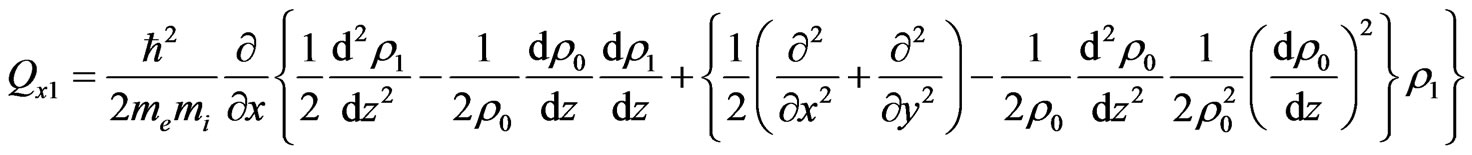 (35)
(35)
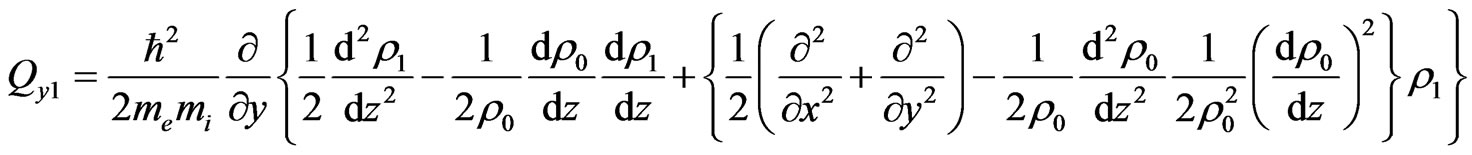 (36)
(36)
 (37)
(37)
Now, Using the expression (10) in the system of equations (30)-(37) maybe written as
 (38)
(38)
 (39)
(39)
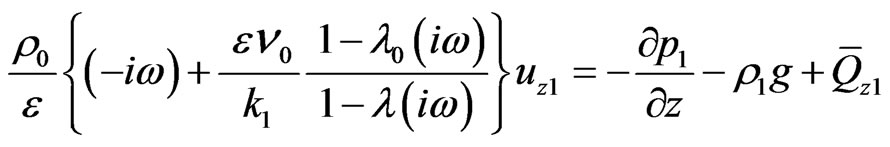 (40)
(40)
 (41)
(41)
 (42)
(42)
 (43)
(43)
 (44)
(44)
 (45)
(45)