1. Introduction
Dark matter is generally believed to account for the approximately flat velocity curves characteristic of spiral galaxies. Observations of the colliding “bullet cluster” galaxies 1E0657-56 provide further evidence for the existence of dark matter. However, some physicists believe the observed flat velocity curves indicate the law of gravity must be modified at large distances according to MOdified Newtonian Dynamics (MOND). Recently Merritt [1] argued for MOND by claiming dark matter models cannot account for the acceleration threshold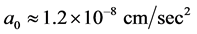 
and the (
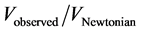) relation emerging from the MOND approach [2] .
2. Purpose
The purpose of this paper is to evaluate the validity of Merritt’s claim by considering a specific model based on dark matter, the holographic large scale structure (HLSS) model [3] . The HLSS model was developed within the LCDM paradigm and employs the holographic principle based on thermodynamics and general relativity [4] . This note shows the HLSS model can account for both the MOND acceleration threshold and the (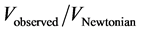
) relation.
3. Analysis
In the HLSS model, galaxies with total mass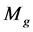 
inhabit spherical holographic
screens with radius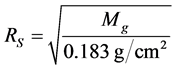 
if the Hubble constant
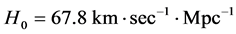. The HLSS model considers galactic matter density
distributions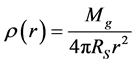
, where r is the distance from the galactic center.
The spherical isothermal halo of dark matter, with radius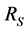 
and mass
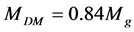, has density distribution 
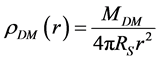so the dark matter mass within radius R is
. There is no singularity in the galactic matter density distribution 
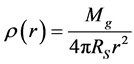because mass inside a core volume of
radius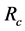 
at the galactic center is concentrated in a central black hole with
mass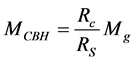 
[3] . Radial acceleration at radius R due to dark matter is then
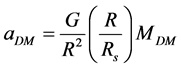. At radii R sufficiently distant from the galactic
center that total baryonic mass of the galaxy ![]()
can be treated as concentrated at the galactic center, Newtonian radial acceleration resulting from
baryonic matter is![]()
. The radius ![]()
where ![]()
is found from
![]()
Since ![]()
and![]()
, ![]()
, and at that radius
![]()
consistent with the MOND estimate![]()
.
Another indication that the MOND acceleration ![]()
is a natural scale in the dark matter based HLSS model involves the situation at the radius ![]()
of the spherical holographic screen. Then the Newtonian assumption, that total galactic mass can be considered as concentrated at the galactic center, is certainly mathematically justified. There, the sum of radial acceleration from dark matter and radial acceleration from baryonic matter is
![]()
Using
![]()
then yields
![]()
equal to the estimated MOND acceleration![]()
.
The tangential velocity V at radius R is related to radial acceleration ![]()
by![]()
. So, the ratio (![]()
) is approximately
![]()
resulting in
![]()
Then, when![]()
,
![]()
as noted by Merritt [1] . Next, using
![]()
and
![]()
results in
![]()
When ![]()
and
![]()
again as noted by Merritt [1] . Since ![]()
when![]()
, using
![]()
and ![]()
gives
![]()
also known as the baryonic Tully-Fisher relation.
Finally, if the Hubble constant![]()
, the cosmological constant![]()
, and the accelerations ![]()
and ![]()
are both consistent with the acceleration
![]()
estimated above.
4. Conclusion
Contrary to Merritt’s claim [1] , this note demonstrates that the HLSS model [3] , based on dark matter, can account for the MOND acceleration threshold, the (![]()
) relation, and the baryonic Tully-Fisher relation. After this paper was accepted for publication, I learned that Man Ho Chan previously reached the same conclusion [5] using a dark matter based analysis independent of the holographic approach used in this paper.
Acknowledgements
I thank the reviewer for important suggestions about how to improve the presentation of these results.