
1. Introduction
Weak interactions have some unique properties that cannot be found in other kinds of interactions. The following points illustrate this claim.
・ Weak interactions do not conserve parity.
・ Weak interactions do not conserve flavor.
・ The time duration of weak processes span many orders of magnitude. For example, the neutron’s mean life is 880 sec whereas that of the top quark is about 10−24 sec [1] . (Here examples of a very long mean life of about 109 years, like that of the 40K nucleus, are omitted because this effect is due to the difference in the quantum mechanical angular momentum of the nuclei involved in the process.)
・ The weak interactions coupling constant is written in units that have the dimension of energy−2, 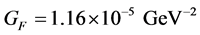 (see [2] , pp. 19, 212).
(see [2] , pp. 19, 212).
These weak interactions properties indicate that its theory should have a specific structure. Another issue is the existence of unsettled problems with the electroweak theory. Some of these problems are mentioned in the second section. Considering this state of affairs, the present work describes elements of a consistent weak interactions theory. As a first step, the discussion is restricted to the simplest case of an elastic neutrino scattering (see [3] ).
A fundamental property of Quantum Field Theory (QFT) is the description of a par- ticle by means of a function the takes the form 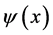 (see e.g [4] , p. 299). Here
(see e.g [4] , p. 299). Here 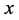 denotes a single set of four space-time coordinates. It means that such a function des- cribes a pointlike particle. Indeed,
denotes a single set of four space-time coordinates. It means that such a function des- cribes a pointlike particle. Indeed, 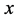 can describe the position of a particle at a given time but not its distribution around this point. Experimental data support the pointlike property of elementary particles (see e.g. [5] ). Evidently, two points cannot collide. Therefore, a mediating field is required for a description of a scattering process of pointlike particles.
can describe the position of a particle at a given time but not its distribution around this point. Experimental data support the pointlike property of elementary particles (see e.g. [5] ). Evidently, two points cannot collide. Therefore, a mediating field is required for a description of a scattering process of pointlike particles.
The need for a mediating field in weak interactions is analogous to a corresponding property of quantum electrodynamics (QED), where Maxwellian fields interact with a pointlike charge of an elementary particle. Electrodynamics is certainly the best phy- sical theory because it has many experimental supports as well as a tremendous number of specific applications in contemporary technology. The present work aims to cons- truct a weak interaction theory that has a certain similarity with QED. In particular, it follows the structure of QED and uses a weak interaction term that is added to the Lagrangian density of the system. Specific aspects of this similarity are described below in appropriate places.
Units where 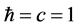 are used. Greek indices run from 0 to 3 and Latin indices run from 1 to 3. The metric is diag.
are used. Greek indices run from 0 to 3 and Latin indices run from 1 to 3. The metric is diag.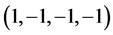 . Square brackets [] denote the dimension of the enclosed expression. In a system of units where
. Square brackets [] denote the dimension of the enclosed expression. In a system of units where 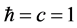 there is just one di- mension, and the dimension of length, denoted by
there is just one di- mension, and the dimension of length, denoted by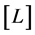 , is used. In particular, energy and momentum take the dimension
, is used. In particular, energy and momentum take the dimension 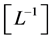 and the dimension of a dipole is
and the dimension of a dipole is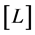 .
.
2. Problems with the Electroweak Theory
Several theoretical problems of the electroweak theory are briefly presented in this section. A fundamental principle used herein is the correspondence between QFT and quantum mechanics. S. Weinberg has used the following words for describing this principle: “First, some good news: quantum field theory is based on the same quantum mechanics that was invented by Schroedinger, Heisenberg, Pauli, Born, and others in 1925-26, and has been used ever since in atomic, molecular, nuclear and condensed matter physics” (see [4] , p. 49). This principle can also be found in pp. 1-6 of [6] . Hereafter, this relationship is called “Weinberg correspondence principle”.
The following review article states that it is now recognized “that neutrinos can no longer be considered as massless particles” (see [3] , p. 1307). It means that the neutrino is an ordinary massive Dirac particle which is described by a 4-component spinor. (The argument also applies to a Majorana neutrino.) This experimental evidence does not fit the original structure of the Standard Model where the neutrino is treated as a 2-com- ponent massless particle [7] . In the following lines it is proved that this property of the neutrinos is inconsistent with expressions that have the factor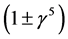 . The factor
. The factor 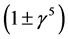 has been proposed for a two-component massless Weil neutrino (see [2] , p. 219, 367). For example, it is used in a description of an electron-neutrino interaction (see [2] , pp. 219-220)
has been proposed for a two-component massless Weil neutrino (see [2] , p. 219, 367). For example, it is used in a description of an electron-neutrino interaction (see [2] , pp. 219-220)
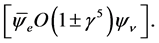 (1)
(1)
Here 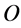 represents an appropriate operator which operates on
represents an appropriate operator which operates on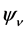 . It turns out that this expression does not hold for a massive Dirac neutrino. Indeed, operating with
. It turns out that this expression does not hold for a massive Dirac neutrino. Indeed, operating with ![]() on a motionless spin-up Dirac spinor, one obtains
on a motionless spin-up Dirac spinor, one obtains
![]() (2)
(2)
Here the ![]() matrices notation is that of [8] , p. 17.
matrices notation is that of [8] , p. 17.
The right hand side of (2) is a Dirac spinor that has an infinite energy-momentum (see [8] , p. 30). It means that the operator ![]() casts a motionless Dirac particle into an unphysical state. Furthermore, a product of two
casts a motionless Dirac particle into an unphysical state. Furthermore, a product of two ![]() matrices is used for a boost of a Dirac particle (see [8] , p. 21). Hence,
matrices is used for a boost of a Dirac particle (see [8] , p. 21). Hence, ![]() commutes with the boost operator. For this reason, the operator
commutes with the boost operator. For this reason, the operator ![]() casts any Dirac spinor into the unphysical state of an infinite energy-momentum. Evidently, every basis of the Hilbert space of a Dirac particle is made of physically acceptable states of this quantum particle. Therefore, a state that has an infinite energy-momentum is not included in a Hilbert space. Hence, the required matrix elements cannot be calculated. This is an example showing that the factor
casts any Dirac spinor into the unphysical state of an infinite energy-momentum. Evidently, every basis of the Hilbert space of a Dirac particle is made of physically acceptable states of this quantum particle. Therefore, a state that has an infinite energy-momentum is not included in a Hilbert space. Hence, the required matrix elements cannot be calculated. This is an example showing that the factor ![]() is inconsistent with the Weinberg correspondence principle.
is inconsistent with the Weinberg correspondence principle.
The factor ![]() is used for adapting the Standard Model to the V-A property of the weak interactions (see [2] , pp. 217-220). The contradiction obtained above indicates that the Standard Model is inconsistent with the V-A property of the weak interactions.
is used for adapting the Standard Model to the V-A property of the weak interactions (see [2] , pp. 217-220). The contradiction obtained above indicates that the Standard Model is inconsistent with the V-A property of the weak interactions.
Let us examine other electroweak contradictions. The ![]() and the
and the ![]() particles are fundamental elements of the electroweak theory. It turns out that the theoretical structure of these particles is inconsistent with fundamental physical requirements. Let us begin with the
particles are fundamental elements of the electroweak theory. It turns out that the theoretical structure of these particles is inconsistent with fundamental physical requirements. Let us begin with the![]() , which are a particle/antiparticle that carry a positive/negative charge, respectively. These particles must perform two different physical tasks: In a weak process they play the role of an interaction mediator that carries the interaction between two fermions. On the other hand, in an electromagnetic interaction they act as a charge carrier and the electromagnetic interaction is mediated by Maxwellian fields.
, which are a particle/antiparticle that carry a positive/negative charge, respectively. These particles must perform two different physical tasks: In a weak process they play the role of an interaction mediator that carries the interaction between two fermions. On the other hand, in an electromagnetic interaction they act as a charge carrier and the electromagnetic interaction is mediated by Maxwellian fields.
It turns out that these two different tasks cannot be accomplished simultaneously. For example, the electromagnetic interaction term is![]() , where
, where ![]() denotes a conserved 4-current that satisfies the continuity equation
denotes a conserved 4-current that satisfies the continuity equation![]() . It is well known that this requirement is satisfied by a Dirac particle (see [8] , p. 24). By contrast, the electro- weak theory is more than 40 years old but there is still no self-consistent expression for the 4-current of the
. It is well known that this requirement is satisfied by a Dirac particle (see [8] , p. 24). By contrast, the electro- weak theory is more than 40 years old but there is still no self-consistent expression for the 4-current of the ![]() (see [9] ).
(see [9] ).
The lack of a consistent expression for the 4-current of the ![]() is implicitly admitted by the general community. Indeed, theoretical groups working in reputable research centers apply unusual procedures in a calculation of the
is implicitly admitted by the general community. Indeed, theoretical groups working in reputable research centers apply unusual procedures in a calculation of the ![]() electromagnetic interactions. Thus, the theoretical group of the D0 facility at Fermilab and that of the LHC facility at CERN use an effective expression for this purpose. (see Equation (1) in [10] and Equation (3) in [11] , respectively). By contrast, calculations of electromagnetic interactions of a Dirac particle are based on a theoretically valid expression.
electromagnetic interactions. Thus, the theoretical group of the D0 facility at Fermilab and that of the LHC facility at CERN use an effective expression for this purpose. (see Equation (1) in [10] and Equation (3) in [11] , respectively). By contrast, calculations of electromagnetic interactions of a Dirac particle are based on a theoretically valid expression.
The origin of this contradiction can be briefly explained. Due to a widely acceptable rule, the following substitution is introduced in order to account for the electromag- netic interactions ![]() (see [12] p. 84). The
(see [12] p. 84). The ![]() Lagrangian density con- tains a product of two functions that contain
Lagrangian density con- tains a product of two functions that contain![]() . Hence, the
. Hence, the ![]() Noether 4-current
Noether 4-current ![]() depends linearly on
depends linearly on![]() . It follows that the electromagnetic interaction term
. It follows that the electromagnetic interaction term ![]() is quadratic in
is quadratic in ![]() and in the electric charge
and in the electric charge![]() . This is inconsistent with Maxwellian electrodynamics, where Maxwell equations are derived from a Lagrangian function which depends linearly on the 4-potential
. This is inconsistent with Maxwellian electrodynamics, where Maxwell equations are derived from a Lagrangian function which depends linearly on the 4-potential ![]() (see [13] , p. 75). Conclusion: the
(see [13] , p. 75). Conclusion: the ![]() has no 4-current.
has no 4-current.
The lack of a consistent expression for the W's conserved 4-current also violates the Weinberg correspondence principle, because the Schroedinger equation has a con- sistent expression for a conserved density and current (see [14] , pp. 53-55).
It can be shown that the electroweak ![]() boson suffers from an analogous con- tradiction where density of a massive particle cannot be defined. Thus, this particle is described by a real function (see [15] , p. 307). For this reason, the
boson suffers from an analogous con- tradiction where density of a massive particle cannot be defined. Thus, this particle is described by a real function (see [15] , p. 307). For this reason, the ![]() boson has no self-consistent expression for density [16] . It should be pointed out that density is the 0-component of the 4-current. And indeed, QFT textbooks do not show a consistent expression for the 4-current of the
boson has no self-consistent expression for density [16] . It should be pointed out that density is the 0-component of the 4-current. And indeed, QFT textbooks do not show a consistent expression for the 4-current of the ![]() boson. Thus, the electroweak
boson. Thus, the electroweak ![]() boson suffers from a contradiction which is analogous to the above mentioned contradiction of the electroweak
boson suffers from a contradiction which is analogous to the above mentioned contradiction of the electroweak ![]() bosons. In particular, a Hilbert space cannot be constructed without a self-consistent expression for density. Hence, the electroweak
bosons. In particular, a Hilbert space cannot be constructed without a self-consistent expression for density. Hence, the electroweak ![]() boson is incon- sistent with the Weinberg correspondence principle, because a Hilbert space is an indispensable element of quantum mechanics (see [4] , p. 49).
boson is incon- sistent with the Weinberg correspondence principle, because a Hilbert space is an indispensable element of quantum mechanics (see [4] , p. 49).
The contradictions of the electroweak theory indicate that a consistent theory of weak interactions is needed. Evidently, experimental data provide clues for a con- struction of such a theory. These issues are discussed in the rest of this work.
3. Fundamental Elements of a Theory of Weak Interaction Dynamics
The weak interaction theory constructed below aims to follow the theoretical structure of QED. Hence, the main problem is how to construct an expression that represents weak interactions in the form of a term of the Lagrangian density of a Dirac particle. In the case of electromagnetic interaction, the 4-current of a Dirac particle is ![]() (see [8] , pp. 23-24), and the corresponding interaction term of the Lagrangian density is (see [12] , p. 86)
(see [8] , pp. 23-24), and the corresponding interaction term of the Lagrangian density is (see [12] , p. 86)
![]() (3)
(3)
It means that the electromagnetic interaction term is the contraction of the 4-vector of the ![]() matrices with the 4-vector
matrices with the 4-vector ![]() of the external electromagnetic potential
of the external electromagnetic potential![]() , where the latter depends on the four space-time coordinates. Here the strength of the interaction is
, where the latter depends on the four space-time coordinates. Here the strength of the interaction is
![]() (4)
(4)
This quantity is a dimensionless Lorentz scalar.
The weak interaction theory described herein abides by the experimental evidence where, in the units![]() , the dimension of the Fermi constant is (see [2] , pp. 19, 212)
, the dimension of the Fermi constant is (see [2] , pp. 19, 212)
![]() (5)
(5)
Hence, the required weak interaction term differs from its electromagnetic counterpart (3), where the electric charge is a dimensionless Lorentz scalar.
Following (5) and the dipole’s dimension![]() , it is assumed here that the weak interactions is a dipole-dipole interaction. Thus, the theory must resolve two problems:
, it is assumed here that the weak interactions is a dipole-dipole interaction. Thus, the theory must resolve two problems:
1) What is the structure of the weak field that mediate the interaction between the weak dipoles?
2) What is the form of the weak interaction term of the system’s Lagrangian density?
A resolution of the first problem is quite simple. The weak field of a weak dipole takes the Maxwellian-like form of an axial dipole. This dipole is carried by every elementary spin-1/2 particle. Hereafter, the strength of this elementary weak dipole is denoted by d. This symbol differs from the mathematical symbol ![]() which is used in integrals, etc. d is a Lorentz scalar that has the dimension
which is used in integrals, etc. d is a Lorentz scalar that has the dimension![]() . The weak dipole strength d takes the same value for all elementary spin-
. The weak dipole strength d takes the same value for all elementary spin-![]() particles, i.e., it is inde- pendent of the particle’s mass. This property is consistent with the universal feature of the Fermi constant
particles, i.e., it is inde- pendent of the particle’s mass. This property is consistent with the universal feature of the Fermi constant![]() . Evidently, an anti-particle carries a weak dipole of the opposite sign. It means that appropriate formulas of dipole fields can be taken from electro- dynamics. Furthermore, this scheme provides unique and well known relationships between the weak source and the associated weak fields. It is explained below that the Maxwellian-like form of the weak field satisfies the required dimension of every term of the Lagrangian density.
. Evidently, an anti-particle carries a weak dipole of the opposite sign. It means that appropriate formulas of dipole fields can be taken from electro- dynamics. Furthermore, this scheme provides unique and well known relationships between the weak source and the associated weak fields. It is explained below that the Maxwellian-like form of the weak field satisfies the required dimension of every term of the Lagrangian density.
The tensorial form of this field has magnetic-like components and electric-like com- ponents. Its explicit structure is (see [13] , p. 65)
![]() (6)
(6)
The calligraphic letters![]() ,
, ![]() and
and ![]() are used in order to distinguish between weak fields and their corresponding electromagnetic fields.
are used in order to distinguish between weak fields and their corresponding electromagnetic fields.
Let us turn to the second problem. Like all other terms of the Lagrangian density, the electromagnetic interaction term (3) is a dimensionless Lorentz scalar. It holds for the interactions of the Dirac particle’s electric charge, which is a dimensionless Lorentz scalar. Hence, the problem is to find the form of an analogous expression for the elementary weak dipole, which has the inherent dimension![]() . The non-covariant formula for the energy of a magnetic dipole
. The non-covariant formula for the energy of a magnetic dipole ![]() interacting with an external magnetic field is (see [17] , p. 186)
interacting with an external magnetic field is (see [17] , p. 186)
![]() (7)
(7)
This formula indicates how to construct the required expression. It must depend linearly on the Maxwellian-like weak field of a weak dipole. The very small limit of the neutrino mass [1] means that in actual experiments the neutrino is an ultrarelativistic particle where![]() . Therefore, a Lorentz transformation of the tensor (6) proves that the absolute value of the vector components and of the axial vector components of this tensor are practically the same (see [13] p. 66)
. Therefore, a Lorentz transformation of the tensor (6) proves that the absolute value of the vector components and of the axial vector components of this tensor are practically the same (see [13] p. 66)
![]() (8)
(8)
In order to construct a Lorentz scalar term for the Lagrangian density of the weak interactions, one must contract the tensor (6) with another tensor which depends on the Dirac ![]() matrices. Evidently, a second rank antisymmetric tensor is required for this purpose. This tensor can be readily taken from the literature (see [8] p. 21)
matrices. Evidently, a second rank antisymmetric tensor is required for this purpose. This tensor can be readily taken from the literature (see [8] p. 21)
![]() (9)
(9)
Let us write down the explicit form of (9) as a ![]() matrix whose entries are the appropriate products of two
matrix whose entries are the appropriate products of two ![]() matrices.
matrices.
![]() . (10)
. (10)
Here the anti-commutation of two different ![]() matrices is used and the denominator 2 of (9) is removed.
matrices is used and the denominator 2 of (9) is removed.
The weak interaction term of the Lagrangian density is obtained from a contraction of (10) and (6), times the scalar factor d, which represents the weak dipole strength. Hence, the term which is analogous to the electromagnetic interaction term (3) is
![]() (11)
(11)
Note that the pure imaginary factor ![]() should not be confused with the indices
should not be confused with the indices![]() . In order to fit to the numerical notation of the
. In order to fit to the numerical notation of the ![]() index, the indices 1, 2, 3 denote the fields' components
index, the indices 1, 2, 3 denote the fields' components![]() , respectively. Hereafter, (11) is called the primary weak interaction term. The form of the left hand side of (11) is analogous to the electro- magnetic interaction term of the Lagrangian density (3). In both cases a
, respectively. Hereafter, (11) is called the primary weak interaction term. The form of the left hand side of (11) is analogous to the electro- magnetic interaction term of the Lagrangian density (3). In both cases a ![]() -dependent quantity is contracted with an external field and the factors
-dependent quantity is contracted with an external field and the factors ![]() respectively denote the intensity of the interaction.
respectively denote the intensity of the interaction.
The structure of the primary weak interaction term (11) satisfies the Lagrangian density requirements. Due to fundamental laws of tensor algebra, the full contraction of the two tensors proves that this term is a Lorentz scalar. The dipole’s field decreases like ![]() (see [17] , p. 182) and it is multiplied by the dipole’s strength of the source, whose dimension is
(see [17] , p. 182) and it is multiplied by the dipole’s strength of the source, whose dimension is![]() . Hence, the dimension of the weak field
. Hence, the dimension of the weak field ![]() is
is![]() . The factor d of the dipole of the particle that interacts with the weak field adds the dimension
. The factor d of the dipole of the particle that interacts with the weak field adds the dimension![]() . It follows that the dimension of the operator of (11) is
. It follows that the dimension of the operator of (11) is![]() , which is the same dimension as that of the electromagnetic 4-potential
, which is the same dimension as that of the electromagnetic 4-potential ![]() of (3). This conclusion proves that the definition saying that the weak field takes a Maxwellian-like form is not arbitrary.
of (3). This conclusion proves that the definition saying that the weak field takes a Maxwellian-like form is not arbitrary.
As stated in the introduction, the purpose of this work is to find a theory of weak interactions processes where flavor is conserved. It means, a description of an elastic neutrino scattering on a Dirac particle. This process is analogous to the elastic scattering of an electron. Thus, the problem is to find the form of the interaction of the weak dipole of a spin-![]() particle with the Maxwellian-like weak field of another spin-1/2 particle. It means, finding the matrix element of the transition of a Dirac spinor from its initial state
particle with the Maxwellian-like weak field of another spin-1/2 particle. It means, finding the matrix element of the transition of a Dirac spinor from its initial state ![]() to its final state
to its final state ![]() due to its interaction with the field
due to its interaction with the field
![]() (12)
(12)
Here ![]() is the weak interaction operator and (12) is analogous to the expression of an elastic scattering of an electron on a charged target (see equation (6.3) in [2] , p. 186).
is the weak interaction operator and (12) is analogous to the expression of an elastic scattering of an electron on a charged target (see equation (6.3) in [2] , p. 186).
The primary weak interaction term (11) is used for obtaining an expression for the integrand of the scattering formula (12). For this end, the identity
![]() (13)
(13)
is used (see [8] , p. 24). The following calculation proves that ![]() of (13) changes dramatically the form of the primary interaction term (11). Indeed, substituting (13) into (11) and using
of (13) changes dramatically the form of the primary interaction term (11). Indeed, substituting (13) into (11) and using![]() , one finds
, one finds
![]() (14)
(14)
In the second line of (14) three terms are multiplied by![]() ,
, ![]() ,
,![]() . In the third line, the
. In the third line, the ![]() are reordered and the the anti-commutation relation
are reordered and the the anti-commutation relation ![]() is used. The pseudoscalar
is used. The pseudoscalar ![]() is substituted.
is substituted.
The three ![]() matrices are antihermitian. Therefore, the first term of (14) is Her- mitian. It is analogous to the three Dirac
matrices are antihermitian. Therefore, the first term of (14) is Her- mitian. It is analogous to the three Dirac ![]() matrices, which are used in the Dirac Hamiltonian. The following calculation shows that also the product of the
matrices, which are used in the Dirac Hamiltonian. The following calculation shows that also the product of the ![]() matrices of the second term of (14) are Hermitian. Indeed,
matrices of the second term of (14) are Hermitian. Indeed,
![]() (15)
(15)
Hence, the two terms of (14) are Hermitian operators which correspond to the vector V and the axial vector A parts of the weak interactions, respectively. Relation (8) means that these terms are contracted with 3-vectors that practically have the same absolute value. It means that the weak interaction theory which is derived above proves that weak processes do not conserve parity. This result is also consistent with the equal weight of V and A in the well known V-A form of weak interactions [18] [19] . It means that the dipole structure of the weak interaction theory developed herein proves that an interaction of a neutrino with a Dirac particle is in accordance with the parity violating V-A form of weak interactions.
4. Concluding Remarks
This work aims to make the first step towards the construction of a consistent weak interaction theory. As such, it examines the relatively simple process of an elastic neutrino scattering. Like the case of other theories, it must take some kinds of ex- perimentally related information that is used as a basis for the mathematical structure of the theory. This work uses just one specific kind of experimental information which is the Fermi constant. The theory uses the dimension of the Fermi constant ![]() and its universal feature. This information is used for constructing a weak interaction term which is added to the Lagrangian density of a Dirac particle.
and its universal feature. This information is used for constructing a weak interaction term which is added to the Lagrangian density of a Dirac particle.
The general structure of the theory is similar to that of QED. It comprises two kinds of physical objects, a weak axial dipole which is associated with a massive Dirac particle and a weak field that mediates the interaction between two weak dipoles. The need for such a field is deduced from the pointlike attribute of an elementary quantum particle.
The mathematical structure of the theory is built on these issues and the result proves that weak interactions do not conserve parity. This theoretical result is in accordance with a well known property of weak interactions. This success encourages a further research in this direction.
The Lagrangian density obtained above describes weak interactions of two spin-1/2 Dirac particles which is mediated by a weak field. In actual cases of scattering ex- periments, one should remove other, much stronger interactions. Therefore, one of the interacting particles must be a neutrino (or an anti-neutrino).
Other aspects of weak interactions should be analyzed. Here are some points:
1) The weak dipole depends on spin orientation. Taking into account that in a neutrino scattering the target is a macroscopic body, one must calculate how a neu- trino interacts with an electron whose wave function is not an eigenfunction of![]() . The same problem arises in a collision of a neutrino with a baryon, where the “proton spin crisis” indicates that the spin orientation of a baryonic quark is practically unde- termined.
. The same problem arises in a collision of a neutrino with a baryon, where the “proton spin crisis” indicates that the spin orientation of a baryonic quark is practically unde- termined.
2) Flavor changing processes should be calculated.
3) The CKM matrix as well as the neutrino oscillation indicate that there are three kinds (called generations) of weak dipoles which interact with each other. In hadrons, weak interactions cause transition within generations and in hadrons and leptons they also cause transition between generations. This evidence certainly complicates the struc- ture of a comprehensive weak interaction theory.