Kinematic and Aerodynamic Modelling of Bi- and Quad-Wing Flapping Wing Micro-Air-Vehicle ()
1. Introduction
Human efforts to mimic flying biosystems such as insects and birds through engineering feat to meet human needs have progressed for hundreds of years as well as motivated mankind creativity, from Leonardo Da Vinci’s drawings to Otto Lilienthal’s gliders, to modern aircraft technologies and present flapping flight research. Recent interest in the latter has grown significantly particularly for small flight vehicles (or Micro- Air-Vehicles) with very small payload carrying capabilities since to allow remote sensing missions where access is restricted due to various hazards. Some of these vehicles may have a typical wingspan of 15 cm, with a weight restriction of less than 100 g [1] . Perhaps the most comprehensive account of insect flight or entomopter to date is given by Ellington [2] [3] [4] , Dickinson et al. [5] and Ansari et al. [6] , while one of the first successful attempts to develop bird-like flapping flight was made by DeLaurier [7] . Although our interest in developing a mathematical and experimental model is on more or less rigid quad wing ornithopter, it is also motivated by the fact that insect and hummingbirds have lightweight, flexible wings that undergo large deformations while flapping, which can increase the lift of flapping wings [8] . It will be of good interest how wing flexibility can be later on adopted. Various flapping wing in biosystems are exemplified in Figure 1, and those addressed in the present wing are the flapping motion of bi-wing system as represented by an eagle, and quad-wing system as represented by a dragonfly. The flapping wing bio-mimicry designs have been created with varied success, for forward or hover mode, but not both, based on observations of hummingbirds and bats [9] .
Among the many potential advantages of flapping flight compared to fixed-wing and rotary-wing flights include increased propulsive efficiency, maneuverability, and stealth. As impressively demonstrated by birds and insects, flapping wings offer potential advantages in maneuverability and energy savings compared with fixed-wing aircraft, particularly in vertical take-off, landing and maneuver dexterity. In comparison to fixed-wing and rotary wing Micro-Air Vehicles, the airfoils of the ornithopter have a flapping or oscillating motion, instead of fixed or in rotary motion, and have a combined function of providing both lift and thrust. The capability of flapping airfoils to produce both lift and thrust minimizes the drag-inducing structures, hence weight. These two advantages potentially allow a high degree of efficiency. As stipulated by Hall and Hall [10] , ornithopters may be able to reach a propulsive efficiency of 85%. The dragonfly has the capability to shift flight modes simply by varying the phase lag between its fore and hind wings [11] . With that observation, a quad-winged flapping system could be conceived as the simplest mechanism that has the capabilities to shift between flight modes [9] . In one of the recent work in developing quad flapping wing micro air vehicle, Ratti [12] has theoretically shown that a flight vehicle with four flapping wings has 50% higher efficiency than that with two flapping wings. Inspired by the flight of a dragonfly, Prosser [13] analyzed, developed and demonstrated a Quad- Winged Air Vehicle (QWAV) which can produce higher aerodynamic performance
![]() (a) (b) (c) (d)
(a) (b) (c) (d)
Figure 1.Comparison of flying biosystems and their modelling as Flapping Wing Ornithopter and Quad-Wing Air Vehicle (QWAV); (a) soaring eagle exhibiting its wing geometry and structural detail; (b) a humming bird, which is the only bird species that ehhibit unique flapping wing characteristic reminiscent of insect; (c) a dragonfly and (d) a model of quad-wing air vehicle [12].
and energy efficiency, and increased payload capacity compared to a conventional (flapping wing) MAV.
Within such backdrop, in the present work, a generic approach is followed to understand and mimic the unsteady aerodynamics of biosystem that can be adopted in the present QWAV. To that end, a simple and workable Quad-Wing-Micro-Air-Vehicle (QVMAV) pterosaur-like ornithopter flight model is developed to produce lift and thrust for forward flight. At the present stage, such model will not take into account the more involved leading edge vortex and wake penetration exhibited by insect flight [1] [2] [3] [4] .
2. Kinematics of Flapping Wing Motion
The flapping wing motion of ornithopters can be generally grouped into three classes, based on the kinematics of the wing motion and mechanism of forces generation; the horizontal stroke plane, inclined stroke plane and vertical stroke plane [4] . The most distinctive characteristic in insect flight is the wing kinematics [6] . As a result from these kinematics, the aerodynamics associated with insect flight are also very different from those met in conventional fixed- and rotary-wing or even bird flight [6] . Based on Ellington’s study [2] [3] [4] , the kinematic of flight produced by the generic wing (semi-elliptical wing) can be classified into the inclined stroke plane, where the resultant force produced by the wing can be separated into vertical and horizontal components, which are lift, thrust and drag, respectively throughout the up-stroke and down- stroke cycle; the inclined stroke plane, where a large horizontal thrust component will be produced; and the vertical stroke plane. For the dragonfly, the quad-wing flight motion is depicted in Figure 2.
![]()
Figure 2. Flight motion of dragonfly (Adapted from [14] ).
3. Theoretical Development of Flapping Wings Generic Aerodynamics
Following the frame of thought elaborated in the previous section, several generic wing planforms are chosen in the present work as baseline geometries for the ornithopter wing Biomimicry Flapping Mechanism, among others the semi elliptical wing, shown in Figure 3, with the backdrop of various wing-planform geometries utilized by various researchers.
The present work resorts to analytical approach to the flapping wing aerodynamic problem, which can be separated into quasi-steady and unsteady models. The quasi-steady model assumes that flapping frequencies are slow enough that shed wake effects are negligible, as in pterosaur and medium- to large-sized birds while the unsteady approach attempts to model the wake like hummingbird and insects. The present aerodynamic approach is synthesized using basic foundations that may exhibit the generic contributions of the motion elements of the bio-inspired quad-wing air vehicle characteristics. These are the strip theory and thin wing aerodynamic approach [21] , Jones modified Theodorsen unsteady aerodynamics [22] [23] , incorporation of leading edge suction [24] [25] . Jones’ modified Theodorsen approach which incorporates Garrick’s leading edge suction without spanwise twist and post-stall behavior was adopted following DeLaurier’s approach, and the computation of lift, drag and thrust generated by pitching and flapping motion of three-dimensional rigid wing in a structured method using strip theory and Jones’ modified Theodorsen approach without camber, leading edge suction and post-stall behavior. Other improvement of the computational model may later on be added based on other observations and work of various researchers. Lifting-surface theory [26] [27] may later be incorporated.
![]()
Figure 3. A generic semi-elliptical ornithopter’s wing planform with the backdrop of various wing-planform geometries [9] [15] - [20] .
Blade element theory has been utilized for flapping wing analysis by many researchers [2] [7] [16] [28] . In the present work, unsteady aerodynamics of a flapping wing using a modified strip theory approach as a simplification of DeLaurier’s and Harmon’s approach for pterosaur flapping-wing aerodynamics is carried out without post-stall behavior. Byl [16] and Malik and Ahmad [29] have applied blade element and DeLaurier’s approach in their work, respectively.
A novel initiative has been introduced by Djojodihardjo and Ramli [19] [20] for separating the wing flapping motion element and carrying out a parametric study on the contribution of each of these elements in the aerodynamic forces generated. These are motivated by the objective to gain insight into the mechanism of lift and thrust generation by itching, flapping and coupled motions, as well as the influence of pitch-flap phase lag for optimization purposes, by also looking into the influence of the variation of the forward speed, flapping frequency and pitch-flap phase lag. The computational logic in the present work is summarized in the Flow-Chart exhibited in Figure 4. The results of DeLaurier’s, Byl’s, Malik and Ahmad’s and Zakaria et al.’s are used for validation.
Computational Procedure
The computational procedure adopted in the present work essentially follows the philosophy outlined in previous section and summarized in Figure 4.
The flapping wing can have three distinct motions with respect to three axes as: a)
![]()
Figure 4. Ornithopter flapping wing aerodynamics computational scheme.
Flapping, which is up and down stroke motion of the wing, which produces the majority of the bird’s power and has the largest degree of freedom; b) Feathering is the pitching motion of wing and can vary along the span; c) Lead-lag, which is in-plane lateral movement of wing.
Flapping angle β varies as a sinusoidal function. β and its rate are given by following equations. The degree of freedom of the motion is depicted in Figure 5.
Flapping angle β varies as a sinusoidal function. The angle β and its rate and pitching angle θ are given by
 ;
;
 ;
;
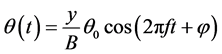 (1)
(1)
where θ0 is the maximum pitch angle, 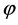 is the lag between pitching and flapping angle and y is the distance along the span of the wing under consideration.
is the lag between pitching and flapping angle and y is the distance along the span of the wing under consideration.
The vertical and horizontal components of relative wind velocity, as depicted in Figure 6, can be expressed as
![]()
Figure 5. Flapping and pitching motion of flapping wing.
![]()
Figure 6. Forces on flapping wing section.
 (2)
(2)
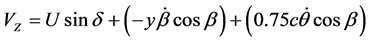 (3)
(3)
For horizontal flight, the flight path angle γ is zero. Also,  is the relative air effect of pitching rate
is the relative air effect of pitching rate 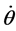 which is manifested at 75% of the chord length [7] . The relative velocity, relative angle between two velocity components ψ and the relative angle of attack can be expressed as
which is manifested at 75% of the chord length [7] . The relative velocity, relative angle between two velocity components ψ and the relative angle of attack can be expressed as
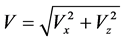 ;
; 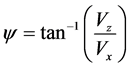 and
and 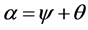 (4)
(4)
The section lift coefficient due to circulation (Kutta-Joukowski condition, flat plate) is given by [7]
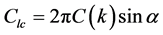 (5)
(5)
dLc can then be calculated by
![]() (6)
(6)
which should be integrated along the span to obtain the flapping-wing lift. Here c and dy are the chord length and spanwise strip width of the element of wing under consideration, respectively. The apparent mass effect (momentum transferred by accelerating air to the wing) for the section, is perpendicular to the wing, and acts at mid chord, and can be calculated as [14] [29]
![]() (7)
(7)
The drag force has two components, profile drag and induced drag where the values for the drag coefficients are assumed to be similar to those associated with basic geometrical cases (such as flat plate, airfoil with tabulated data and the like). To account for profile drag, a factor K is introduced [15] [30] . A maximum value of K of 4.4 as given by Scherer [30] will be used. CDi is induced drag coefficient, and e is the efficiency factor of the wing and is 0.8 for elliptical wing. Total section drag is thus given by
![]() (8)
(8)
The circulatory lift dLc, non-circulatory force dNnc and drag dDd for each section of the wing changes its direction at every instant during flapping. These forces in the vertical and horizontal directions will be resolved into those perpendicular and parallel to the forward velocity, respectively. The resulting vertical and horizontal components of the forces are given by
![]() (9)
(9)
![]() (10)
(10)
and are calculated within one complete cycle, and averaged to get the total average lift and thrust of the ornithopter.
C'(k), F'(k) and G'(k) relate to the Theodorsen function [22] [23] which are functions of reduced frequency k. More sophisticated procedure (which later on will be added and introduced as second method in result and analysis subchapter) can be done by adding Garrick’s [24] expression for the leading edge suction of two dimensional airfoil to be applied on present strip theory model, and also the effect of downwash, w0/U which causes a local induced angle of attack, where it reduces lift [21] .
4. Results and Analysis for Bi-Wing Flapping Ornithopter
4.1. Baseline
The results below are obtained using the following wing geometry and parameters: the wingspan 40 cm, aspect ratio 6.2, flapping frequency 7 Hz, total flapping angle 60˚, forward speed 6 m/s, maximum pitching angle 20˚, and incidence angle 6˚. The computational scheme developed has been validated satisfactorily. Two methods (procedures); first method and second method are shown for insight purpose on force production tolerance. A sample of such validation is shown in Figure 7, which was obtained using aerodynamic strip theory and Theodorsen-Jones modified formulations, where the geometry is similar to Harmon’s [15] and the parameters are relatively close to his.
The following assumptions were made: the pitching and flapping motions are in sinusoidal motion, and the upstroke and downstroke phases have equal time duration. There is incidence angle, which is 6˚ and there is no flight path angle.
The phase lag was assumed to be fixed at 90˚. The Computational Procedure did not incorporate the leading edge suction, wake capture and dynamic stall.
The Average values for lift per flapping cycle calculated using the first and second Computational Procedure are comparable, both for rectangular and semi-elliptical planform. Agreement with Byl’s [16] value of Lift per flapping cycle for modified elliptical planform is only qualitative, which could be understood for the simplicity of our models. The Average lift per flapping cycle computed using the second Computational Procedure for DeLaurier’s pterosaur wing are in excellent agreement with those obtained by both DeLaurier and Zakaria et al, while for the thrust, our second Computational Procedure result agrees with Zakaria et al.’s. The average thrust per flapping cycle calculated using the first Computational Procedure is close to that obtained by Malik et al.
![]()
Figure 7. Lift, thrust and drag forces obtained using the computational procedure outlined in Figure 4 for semi-elliptical planform wing.
Companion studies is carried out to investigate the influence of individual contributions of the pitching-flapping motion and their phase lag on the flight performance [31] [32] . The calculation is performed on rectangular wing. Results obtained as exhibited in Figure 8 show that for the lift, the pitching angle dominates the force, while for the thrust, the flapping angle. The drag is also dominated by flapping effect.
4.2. Parametic Study of Bi-Wing Flapping Ornithopter
A parametric study is carried out to assess the influence of some flapping wing motion parameters to the flight performance desired. The study considers the following parameters: the Effect of Forward speed, the Effect of Flapping Frequency, the Effect of Lag Angle, the Effect of Angle of Incidence and the Effect of Total Flapping Angle.
The results are exhibited in Figure 9. An interesting result is exhibited by Figure 9(b) and Figure 9(c), where the wingbeat frequency has been varied and the thrust is consistently increased with the increase of the wingbeat frequency, while the lift increases only slightly. If reference is made to Pennycuick’s Formula (1) [33] and Tucker’s formula [34] to correlate wing-span and wing area of birds, the present ornithopter model operating frequencies as anticipated in Figure 8 are close to the operating flapping frequency values of selected birds shown in Figure 10.
4.3. Quad-Wing Flapping Ornithopter
Following similar kinematic and aerodynamic model and aerodynamic computational
![]()
Figure 8. The contribution of individual element of the pitching-flapping motion.
![]()
Figure 9. Parametric Study on the influence of forward speed (a); flapping frequency ((b), (c)); flapping-pitching phase lag (d), angle of incidence (e), and total flapping angle (f) on cyclic lift, drag and thrust (for a rectangular planform wing).
![]()
Figure 10. Comparison of basic performance of ornothopter and entomoptert models, and bird & insects.
scheme as elaborated in previous sections, a computational study is carried out for a quad-wing flapping ornithopter, using similar dimensions as the bi-wing flapping ornithopter. The wing dimensions are such that performance comparison between the bi-wing and quad-wing ornithopter can be made, such as the total wing area should be similar for both. The influence of individual contributions of the pitching-flapping motion and their phase lag on the flight performance is carefully modelled and investigated. Without loss of generality, for simplicity the calculation is also performed on rectangular wing.
Results obtained as exhibited in Figure 11 show the lift produced for various scenarios involving phase combinations between flapping and pitching motions of individual fore- and hind-wings. Table 1 summarizes the average forces per cycle for the selected scenarios.
![]()
Table 1. Average forces for all specifications.
![]()
Figure 11. Lift, thrust and drag forces for flapping and pitching motion of the fore- and hind-wing of quad-wing.
5. General Observation
The computational results for simplified modelling of both bi-wing and quad-wing ornithopters are meant for better understanding of the key elements that produce Lift and Thrust Forces for these ornithopters, as well as a guideline for developing a simple experimental model that can easily be built. More sophisticated computational and experimental model can be built in a progressive fashion, by superposing other key features. To gain better insight into the kinematic and aerodynamic modelling of bi-wing and quad-wing ornithopters, comparison will be made on the basic characteristics and performance of selected ornithopter models with those of selected real birds and insects.
The most noticeable of these changes is the phase difference between forewing and hind wings, defined as the phase angle by which hindwing leads the forewing. When hovering, dragonflies employ a 180˚ phase difference (out of phase), while 54˚ - 100˚ is used for forward flight. When accelerating or performing aggressive maneuvers, there is no phase difference between the two wings (0˚ in phase) [35] .
Table 1 also shows the influence of fore and hind wings phase difference to the production of lift, drag and thrust, computed using the present generic and simplified scheme. The lift produced for 180˚ phase difference between the fore- and hind-wings is the highest among other flight cases. However, the thrust produced for 90o phase difference between the fore- and hind-wings is the highest among other flight cases, giving the best performance attitude for forward flight mode.
Wang and Russel [14] reported that the vorticity field simulated using CFD computation for double wing is complex and not readily related to the computational results for lift and thrust, although on the average, the wing motion creates a downward flow and thus an upward net force on the wings [14] . Figure 12 shows the comparison of lift force generated using the present generic simplified model to the result of Wang and Russell [14] .
![]()
Figure 12. Comparison of Lift computed using the present simplified and generic model and Wang and Russel [14] results, for 1800 phase angle between fore- and hind-wings, which is very qualitative, for proof of concept considerations.
Although quantitatively the comparison shows some discrepancies, qualitatively both results show similar behaviour. Such result could lend support to the present kinematic and aerodynamic modeling of quad-wing ornithopter with non-deforming wing, which can progressively be refined to approach the real biosystem flight characteritics, such as those of dragonfly and other related entomopters.
For this purpose, Figure 10 has been prepared as an extension of the earlier table presented in [19] and [20] , to obtain an insight of the flight characteristics and basic performance of ornithopter models, and birds and insect. Figure 10 exhibits the ratio of the lift per cycle calculated using the present simplified computational model and those obtained by other investigators; for comparison, the weight per wing-span of a selected sample of birds are also exhibited. Although the comparison is by no means rigorous, it may shed some light on how the geometrical modelling and the flapping motion considered in the computational model may contribute to the total lift produced and how further refinement could be synthesized. A remark is in order regarding the viscous effects. Figure 13, adapted and extended from Müller [36] , shows that the Reynolds number of Flapping MAV should be in the order of 1.0 ´ 104 to 1.0 ´ 104. Shyy et al. [37] studied laminar airfoils specifically designed for flapping flight within this Reynolds number regime. Their study shows that for all airfoils, the CL/CD ratio exhibits a clear Reynolds number dependency. For Re varying between 7.5 ´ 104 and 2.0 ´ 106, CL/CD changes by a factor of 2 to 3 for the airfoils tested.
Except for a very thin airfoil UF developed by Shyy [37] , the range of angle-of-attack within which aerodynamics is satisfactory becomes narrower as the Reynolds number decreases. Another airfoil, S1223 exhibits a wider range of acceptable angles-of-attack. At Re about 7.5 ´ 104, the situation is quite different. UF, the thinner airfoil with identical camber, exhibits substantially better aerodynamic performance while maintaining
![]()
Figure 13. Reynolds number range for flying bio-systems and flight vehicles.
a comparable range of acceptable angles-of-attack. However, in the present study, viscosity effects are taken into account following the approach and results of DeLaurier [7] , using the computational formulation as given in the present paper as a simplified approach to the problem, but validated through comparison with comparable experimental results range. Such approach can be justified as a preliminary step towards more accurate approach and to develop simple flapping ornithopter MAV.
6. Discussions
The present work has been performed to assess the effect of flapping-pitching motion with pitch-flap phase lag in the flight of ornithopter. In this conjunction, a computational model has been considered, and a generic computational method has been adopted, utilizing two-dimensional unsteady theory of Theodorsen with modifications to account for three-dimensional and viscous effects, leading edge suction and post-stall behavior. The study is carried out on rectangular and semi-elliptical wing planforms. The results have been compared and validated with others within similar unsteady aerodynamic approach and general physical data, and within the physical assumptions limitations; encouraging qualitative agreements or better have been indicated, which meet the proof of concept objectives of the present work. For the bi-wing flapping ornithopter, judging from lift per unit span, the present flapping-wing model performance is comparable to those studied by Byl [16] , while DeLaurier’s pterosaur model [7] is of larger order of magnitude and comparable to Bald Eagle.
The analysis and simulation by splitting the flapping and pitching motion shows that: (a) the lift is dominantly produced by the pitching motion, since the relative airflow effect prevailed along 75% of the chord length. (b) The thrust is dominated by flapping motion. The vertical component of relative velocity increases significantly as compared to the horizontal components, which causes the force vector produced by the flapping-pitching motion to be directed towards the horizontal axis (thrust axis). (c) The drag is dominated by the flapping motion, due to higher relative velocity as well as higher induced drag due to circulation.
For the quad-wing ornithopter, at the present stage, the simplified computational model adopted verified the gain in lift obtained as compared to bi-wing flapping ornithopter, in particular by the possibility of varying the phase lag between the flapping and pitching motion of individual wing as well as between the fore-and hind-wings.
7. Conclusion
A structured approach has been followed to assess the effect of different design parameters on lift, thrust, and drag of an ornithopter, as well as the individual contribution of the component of motion. These results lend support to the utilization of the generic modelling adopted in the synthesis of a flight model, although more refined approach should be developed. Various physical elements could be considered in developing ornithopter kinematic and aerodynamic model. More refined aerodynamic computational methods, such as CFD or lifting surface methods can be utilized for refined modeling. In retrospect, a generic physical and computational model based on simple kinematics and basic aerodynamics of a flapping-wing ornithopter has been demonstrated to be capable of revealing its basic characteristics and can be utilized for further development of a flapping-wing MAV. Application of the present kinematic, aerodynamic and computational approaches shed some light on some of the salient aerodynamic performance of the quad-wing ornithopter.
Acknowledgements
The authors would like to thank Universiti Putra Malaysia (UPM) for granting Research University Grant Scheme (RUGS) Project Code: 9378200, under which the present research is carried out.
Nomenclature
AR = aspect ratio
B = semi-wingspan
c = chord
CL = Lift Coefficient
CD = Drag Coefficient
CDi = induced Drag Coefficient
C(k) = Theodorsen function
C(k)jones = modified Theodorsen function
Cdf = drag coefficient due to skin friction
dDcamber = sectional force due to camber
dDf = sectional friction drag
dFx = sectional chordwise force
Fx = x (horizontal) component of the resultant pressure force acting on the vehicle
Fz = z (vertical) component of the resultant pressure force acting on the vehicle
f, g = generic functions
h = height
i = time index during navigation
j = waypoint index
dL = sectional lift
dy = width of sectional strip under consideration
dN = sectional total normal force
dNc = sectional circulatory normal force
dNnc = sectional apparent mass effect
dt = time step
dT = sectional thrust
dTs = leading edge suction force
F(k) = Theodorsen function real component
G(k) = Theodorsen function imaginary component
![]() = plunging rate
= plunging rate
k = reduced frequency
L = total lift
Lfore = lift force of fore-wing
t = time
T = total thrust
U = flight velocity
V = relative velocity at quarter chord point
Vx = flow speed tangential to section
Vrel = relative velocity
Vi = induced velocity
w0 = downwash velocity at ¾-chord point
Г = circulation
ρ = air density
β = flapping angle
β0 = maximum flapping angle
θ = pitching angle
![]() = pitching rate
= pitching rate
![]() = pitching acceleration
= pitching acceleration
θ0 = maximum pitch angle
θhindwing = effective pitching angle of hind-wing
![]() = angle of flapping axis with respect to flight velocity (incidence angle)
= angle of flapping axis with respect to flight velocity (incidence angle)
![]() = mean pitch angle of chord with respect to flapping axis
= mean pitch angle of chord with respect to flapping axis
f = lag angle between pitching and flapping angle
δ = incidence angle
α = relative angle of attack
α’ = flow’s relative angle of attack at three-quarter chord point (DeLaurier)
α0 = zero-lift angle
αTheodorsen = phase angle of Theodorsen function
ηs = efficiency coefficient
ω = flapping frequency
![]()
Submit or recommend next manuscript to SCIRP and we will provide best service for you:
Accepting pre-submission inquiries through Email, Facebook, LinkedIn, Twitter, etc.
A wide selection of journals (inclusive of 9 subjects, more than 200 journals)
Providing 24-hour high-quality service
User-friendly online submission system
Fair and swift peer-review system
Efficient typesetting and proofreading procedure
Display of the result of downloads and visits, as well as the number of cited articles
Maximum dissemination of your research work
Submit your manuscript at: http://papersubmission.scirp.org/
Or contact aast@scirp.org