Received 10 May 2016; accepted 27 June 2016; published 30 June 2016

1. Introduction
![]()
Table 1. Summary of various tests for time varying nuclear decay including alpha decay, beta minus decay and beta capture. The date of peak decay was somewhat variable with year from about Dec 15 to March 1 even for 10 year continuous experiments of the same radionuclide.
The longest running radioactive decay data came from Siegert et al. at Physikalisch-Technische, Bundesanstalt (PTB) [1] and Parkhomov at Moscow State University [6] , who gathered continuous data over 11 and 10 years respectively. Alburger et al. [4] from Brookhaven National Laboratory also published several years of data which overlapped two years of the PTB data with reasonable agreement, even though they involved different radioisotopes. Figures 1-4 show the German, Russian and Brookhaven data. We should note that Tower [7] did a statistical analysis that indicated about 50% of the annual variation observed in the Brookhaven data could be ascribed to temperature and humidity variations.
While these results [1] - [6] are the first to show annual variations in radioactive decay rates in controlled and stable environments, other experimental results have shown variations in beta decay rates due to extreme environmental factors. Beta decay and beta capture are understandably affected by environmental factors that change the electronic orbitals around the nucleus either in shape or population. No research we have seen has shown any ability to influence alpha decay rate such as in 238Pu. Yet in the controlled environment of the PTB experiments, the annual alpha decay rate variations of 238Pu (strong interaction) matched the decay rate variations of the beta emitter 154Eu (weak interaction). This equality of variation between strong and weak decay rates would suggest that something more basic must be happening.
Several authors have proposed explanations. Jenkins [9] proposed that the distance to the sun was the primary factor since the Earth’s orbit is ±1.7% elliptical. This hypothesis led to very large predicted variations in decay rate for spacecraft and was convincingly disproved by Cooper [10] using 238Pu power data from the NASA Cassini mission. Norman [11] showed no Earth-Sun rate correlations for 5 other alpha and beta decays.
2. A New Experiment to Investigate Potential Cause of Time Varying Radioactive Decay Rates
2.1. Experiment Description
Overview: In searching for a common cause that affected both strong and weak interactions, we hypothesized variations in Planck’s constant h. Such a variation has been searched for using quasars by King [12] and Webb [13] . King found 4.2 σ evidence in favor of dipole variations in the fine structure constant α in the distant cosmos-which contains h, and Webb found 3.6 sigma evidence (19 ± 5 ppm for z > 1 quasars). The present experiment was set up to be unusually sensitive to variations in Planck’s constant while being purely electromagnetic. If it showed similar annual effects corresponding to h peaking in January-February, then temporal variations in Planck’s “constant” would be a prime candidate.
As with any tunneling process, the tunnel rate has an h in the denominator of the exponential which would increase the tunnel current when h is larger. This was hypothesized to be the cause driving the time variations in
![]()
Figure 1. Plot of the 226Ra PTB data [1] (15 years) from Fischbach et al. [8] where count rate is plotted vs. time along with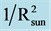 . The peak of the red curves is about Jan 3 each year while the decay rate appears to peak from early January through late February with a mean about Jan 30.
. The peak of the red curves is about Jan 3 each year while the decay rate appears to peak from early January through late February with a mean about Jan 30.
![]()
Figure 2. Russian decay data (pulses per second) for 60Co, 90Sr and 239Pu. 60Co and 90Sr (beta decay/5 and 20 year half life) showed obvious annual variations while 239Pu (alpha decay/26,000 yr half life) did not. The vertical bars mark Jan 1 of each year. Graph from Parkhomov [6] .
nuclear decay rate. In the case of tunnel diodes there are two h effects-the usual h in the denominator of the exponent and also the h2 in the size of the atoms and thus the thickness of the barrier. Since the shape of the nuclear potential does not depend on h, it does not have this additional h2 in the numerator.
![]()
Figure 3. Plot of the BNL data over a 4-year period. Best fit sinusoidal peak was Feb 9. Plot from Alburger [4] .
![]()
Figure 4. Simultaneous plots for a two year overlap in data between the BNL and PTB decay experiments [7] . Pearson Correlation Coefficient r = 0.66, N = 39, Prob = 5.8 × 10−6. Plot from Alburger [4] . Sine wave is 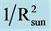 which peaks about Jan 3 each year. The two sets of data correlate to a high level of statistical significance (5.8 × 10−6) even though 32Si is a beta emitter (weak interaction) while 226Ra is an alpha emitter (strong interaction).
which peaks about Jan 3 each year. The two sets of data correlate to a high level of statistical significance (5.8 × 10−6) even though 32Si is a beta emitter (weak interaction) while 226Ra is an alpha emitter (strong interaction).
The result of this the additional factor of h2 in the numerator for electron tunneling was that nuclear decay would have an h in the denominator of the exponent while tunnel current would have an h in the numerator of the exponent. Thus based on the hypothesis of an annual variation in h, the tunnel diode and nuclear effects were predicted to be 180 deg out of phase in their annual variation. This means that minimal Esaki tunnel current would correspond to maximum h and should occur in the Jan-Feb time frame each year. This 180 deg phase shift was verified in the tunneling experiments described below, where the minimum tunnel current (maximum h) was about Jan 1 of each year. The annual variation in the current was 826 ppm peak-to-valley, about half of the typical variation of reported nuclides.
Experiment Design: The experimental layout is a simple circuit as shown in Figure 5. It had 7 features which were designed to maximize the accuracy of the data and to minimize/remove any environmental variations.
1) To average out any component variations and provide more accuracy, five Esaki diodes are connected in parallel and are driven by a stable current source set to 1.0 milliamp―a point about half way up to the first I-V maximum beyond which the negative resistance region would begin. Thus the experiment was operated in the simple mode of electron tunneling through a barrier.
2) The drive current was monitored using a precision resistor and an 8.5 digit multi-meter (DMM).
3) The voltage across the Esaki diodes was monitored by another 8.5 digit DMM.
4) Both DMM’s were zero calibrated periodically with negligible drift.
5) All the diodes and the current resistor were bonded to a copper plate which was temperature controlled to 39.9˚C ± 0.2˚C. The small temperature variations were monitored and recorded.
6) The copper plate is mounted inside a metal box inside a large mesh screened box which includes the DMM’s as well to eliminate potential microwave interactions.
7) All experimental parameters were sampled and recorded automatically every 10 seconds, providing over 8000 measurements every 24 hours.
The six critical components are all listed below for precise specification:
1) Current source XDL35-5P from Sorensen,
2) Precision resistor 500 ohm HR103 from Precision Resistor,
3) Two DMM’s AT3458A-002 high stability option from Agilent,
4) Esaki tunnel diodes MP1603 from Mpulse Microwave,
5) Temperature controller CN7553 from Omega,
6) Temperature monitor 8-channel USB-TC from Measurement Computing.
A National Instruments LabVIEW program was set up to sample the DMM output and temperature sensors automatically every 10 seconds (about 8000 times per day), and the data was written to a data file each midnight.
![]()
Figure 5. Diagram of the Esaki diode tunneling experiment. The input current comes from a stable source and is measured by its voltage drop across a precision resistor. The voltage drop across the five parallel Esaki diodes are also measured precisely as well as the plate temperature, which is tightly controlled.
The 24 hour average of each day’s data became a single data point in the annual variation experiment. The temperature of the tunnel diodes and the exact current from the current source were also measured. These current and temperature measurements were used to correct the measured voltages to remove the effect of the small temperature and drive current variations.
2.2. Computation of the Expected Gain for Variations in Planck's Constant
In the classical calculation of tunneling current we get an expression that has a constant related to available filled and unfilled electronic states on both sides times an exponential of an integral as shown in Equation (1), where h = Planck’s constant, mE = mass of the electron, eE = charge of the electron, V(x) the barrier voltage as a function of position across the barrier thickness xb, and ΔV = the voltage applied across the diode. We worked in the low voltage linear range which gives the ΔV in front.
 . (1)
. (1)
Approximating V(x) for an Esaki diode as a linear barrier voltage 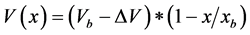 across a barrier thickness xb, we get the simpler expression in Equation (2) which will show the key physics.
across a barrier thickness xb, we get the simpler expression in Equation (2) which will show the key physics.
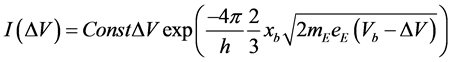 . (2)
. (2)
Since the thickness of the barrier is determined by the size of the atoms, which in turn is proportional to h2, we have a final expression in Equation (3), where ho is the nominal value for Planck’s constant and xb is the nominal atomic thickness of the tunnel barrier at the standard value of h = ho.
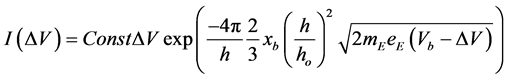 . (3)
. (3)
In this experiment current I is kept constant, resulting in a change in voltage with a change in h. The partial derivative equation can be found by differentiating Equation (3) with respect to I and h as shown below to solve for the fractional change in measured voltage across the tunnel junction as a function of the fractional change in Planck’s constant.
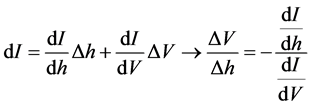 . (4)
. (4)
By differentiating Equation (3) above, we can find both partial derivatives. Then applying the nominal values given below for the 8 nm gap typical of an Esaki tunnel diode, the 1100 mV bandgap of Silicon, our 15 mV set tunnel voltage chosen in the experiment, and assuming our mean value for Planck’s constant is the usual reported value, we get a tunneling gain of about 41, as shown in Equation (8). This increased sensitivity to changes in Planck’s constant h was, of course, why we chose this experiment design.
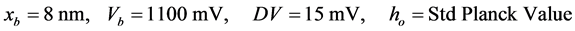 (5)
(5)
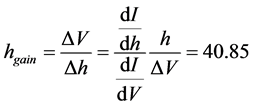 . (6)
. (6)
For later use note that the tunneling exponential by itself is about −56.9, suggesting that a constant voltage current monitoring test would have shown about 40% more sensitivity than the constant current experiment design we did use.
![]() . (7)
. (7)
2.3. Experimental Data Format
The key data collected during the Esaki diode experiment consisted of two voltage readings (the voltage across the precision resistor to measure current and the voltage across the Esaki diode array to measure its resistance). We also have five different temperature sensors monitored simultaneously to track and remove any environmental variations, and all the outputs are sampled automatically every 10 seconds (over 8000 measurements per day).
A sample of the data is shown in Figure 6. During the 941 day experiment, there were 7 missing days of data due to occasional hardware and software issues plus two 10 hour periods when the data acquisition system was down. The missing days were 10/18/2011, 11/5-6/2011, 11/21-22/2011, 1/4-5/2012. The two missing 10 hour periods also occurred when the data acquisition system was down. The remaining 14 hours were averaged for those two days.
There was also a period of about three weeks in 2012 when the calibration was not working for the current DMM. That period has a small bias on the current, which was manually removed as shown below. The DMM was replaced with a backup identical model for the rest of the experiment.
To compare the data from this experiment to the decay data, we note that decay rate is essentially current―the number of particles per second crossing the nuclear barrier. If the resistance of the nuclear barrier drops (by some unknown process), then the decay current goes up. In the Esaki diode experiment, for practical convenience we set the current constant and watched the voltage change, which is the inverse of the nuclear experiment which keeps the nuclear potentials constant and watches the current change. Thus our Esaki voltage data at constant current is inherently 180˚ out of phase with the Esaki current data at constant voltage. Since we predicted that the Esaki current data would be 180 deg out of phase with the radioactive decay rate data, this would mean that the Esaki voltage data would be in phase with the radioactive decay data-as verified below.
2.4. System Calibration
While we have designed the experiment for maximum stability, we must always expect some modest drifts in key parameters. To correct for the small drifts in temperature and drive current we need to calibrate the sensitivity of each one. First we calibrate the Esaki voltage dependence on the voltage measured on the precision current resistor as shown in Figure 7. This will be used to correct the Esaki data for small current fluctuations out of the current source.
1) Current Shift Calibration: To measure the effect of small current shifts, we varied the drive current over a range about our chosen nominal operating condition and recorded the data for the DMM’s. The linear calibration is shown in Equation (8).
![]() . (8)
. (8)
2) Temperature Shift Calibration: Next we calibrated the Esaki and Current voltage dependences on the temperature of the copper plate to which the Esaki diodes and the precision resistor to measure the current are all cemented. We turned off the heater to cool down the plate and then turned it back on to gather the data shown in
![]()
Figure 6. Sample of the data collected every 10 seconds over the 941 day experiment.
Figure 8. This was used to correct the Esaki and Current data for small temperature fluctuations in the copper plate. The quadratic calibrations are shown in Equation (9) and Equation (10).
We note that the shift in the measured current from the current source as a function of the temperature of the copper plate were very small-consistent with the athermal design of this high quality resistor. With a copper plate temperature variation of only ±0.2C during the experiment, this calibration would produce a change in current of only 0.2 ppm―almost negligible although the shift versus time was included in the data analysis.
The shift of the Esaki voltage with temperature was definitely significant, and its correction substantially improved the quality of the data shown later with and without that correction.
![]() . (9)
. (9)
![]()
Figure 7. The calibration of the Esaki voltage versus voltage across the current measuring resistor was done to remove small current fluctuations from the data.
![]()
Figure 8. The Esaki voltage was measured when the Cu plate heater was turned off and then on, and the variations in Esaki voltage versus plate temperature are shown on the left. A similar process was used to measure current voltage versus Esaki plate temperature. A quadratic fit was used for calibration purposes to remove plate temperature variation effects from the data.
![]() . (10)
. (10)
3) Data Correction Process for current and temperature drift: The following formula was used to correct the Esaki voltage (VE) for plate temperature fluctuations and for current source fluctuations. We basically added the voltage shift calibrated above between the nominal operating condition and the present operating condition. The intent was to add in the small corrections due to the ±0.2C temperature shifts on the test plate and the very small current shifts from our current source. This correction process relied on the stable operation of the current measuring resistor and our 8.5 digit DMM’s.
![]()
2.5. Data Analysis
We begin by plotting the raw voltage from the Esaki tunnel diode array in Figure 9. We see what appears to be an annual oscillation as predicted, but we also see an even larger background drift-about 1.5% over the 2.7-year period. We hypothesize that there was slow thermal charge migration through the barrier of the Esaki diodes over the 2.6 years due to the constant voltage and the 40˚C temperature. With the computed tunneling exponent of −56.9, a change in the tunnel current could be created by a change in the barrier voltage by about 1.5%/56.9 = 264 ppm. We also see what appears to be a clear one month transient at the start of the experiment, and to be conservative we drop the first three months from further analysis, leaving us with almost 2.4 years of continuous data.
![]()
Figure 9. The raw Esaki voltage is plotted here vs time showing annual oscillations plus a long-term drift attributed to a 264 ppm change in barrier voltage over time due to charge annealing. A one month initial transient is obvious, and to be conservative, the first 3 months (90 days) are eliminated from the data set-leaving almost 2.4 years of data to process.
To remove the long term drift in the Esaki tunnel diodes, we fit the 2.4 years of data with a linear term plus an exponential. The best-least-squares solution is shown in Figure 10 left, and the oscillatory signal remaining after subtracting the drift is shown in Figure 10 right.
Now we want to do the temperature corrections as measured in Section 2.4. Figure 11 shows all the temperatures recorded in the experiment plotted versus time.
We want to repeat this same process with the calibrated data that should remove the effects of temperature variations and current variations from the data. However, we first have to correct a 12-day period when the current source DMM was out of calibration. The calibration function had stopped working properly and was not caught. Once it was recognized, an identical backup DMM was brought in to replace it-with properly functioning calibration. The effect of this lost calibration was a bias for those 12 days as shown on the left of Figure 12.
When we add the bias correction back into the current voltage data, the annual variation in the current source becomes quite clear, shown in Figure 12 right. This annual voltage response was not expected in the high quality current source and is about 60 - 65 ppm peak-to-valley-quite small compared to the 1000 - 3000 ppm variations seen by radioactive isotopes, but intriguing in its own right. We will revisit this result later. We do note
![]()
Figure 10. The best linear + exponential fit to the raw data is shown on the left for the 2.4 years of data used. After its subtraction we get the annual oscillations shown on the right. The data plotted has not yet been corrected for current and temperature variations.
![]()
Figure 11. The 5 measured temperatures are plotted here over the full 941 days of the experiment. Note that an air conditioning problem raised all the temperatures except for the Esaki plate temperature toward the end of the period. The Esaki plate temperature had been set around 40˚C to keep it controllable under all outside temperatures, and it maintained 39.9C ± 0.2C over the full period.
![]()
Figure 12. The raw current voltage data is plotted on the left with its 12 days of no bias removal. When the bias is corrected for those 12 days, the annual fluctuations of the current source are clear, although much smaller than the tunnel diode annual fluctuations―about 60 - 65 ppm peak-to-valley. These current fluctuations are in phase with the radioactive decay data, peaking in the January-February period each year.
that this data shows peak current in the Jan-Feb period just like the radioactive decay data. This is opposite to the Esaki diode data, as was discussed above, due to the extra factor of h2 in the atomic size of the barrier thickness.
Now that the calibration of the current DMM has been fixed, we use the current data plus the temperature data averaged over the day to correct the Esaki voltage for temperature and current fluctuations. Since the variations over any day are quite small and the corrections are close to linear, this should be accurate. Figure 13 shows the raw and the corrected data together by adding 0.005 to the raw data. The data corrected for temperature and current fluctuations is much smoother indicating proper correction. However, the correction impact is quite small compared to the annual oscillations.
Notice that the effect of the lab temperature rise at the end of the experiment period has been removed by the temperature correction.
We next did a best-least-squares fit to the Esaki voltage data with a sine wave to get the following results-an annual 850.5 ppm variation in the tunnel diode current:
Mean Value = 14.97 mV Peak to Valley Sine = 0.01273 mV
Peak to Valley/Mean = 850.5 ppm Sine Phase = −1.273 deg = Dec 31
Using the estimated h gain from above of 40.85, we get an estimated annual variation in Planck’s parameter h of 20.8 ppm peak-to-valley.
2.6. Annual Variations in the Current Source
Now let us return to consider the second sinusoidal oscillation from the current source and its sinusoidal fit as shown in Figure 14. While it is much smaller, it is clearly much larger than the noise level and also clearly sinusoidal with a one year period. Since tunnel diodes are not used in general purpose electronics, we would expect a much smaller variation, and in fact is about 55 ppm rather than 850 ppm that we saw in the tunnel diode data. Assuming that our estimated gain for the tunnel diode of 40.85 is about correct, then this would correspond to a gain of about 2.7-much smaller as expected-consistent with linear sensitivities to h in feedback loops typical of stabilized current sources. Without more detailed knowledge of the design of the current source, we cannot be more quantitative.
We did best-least-squares fit to the current voltage data with a sine wave to get the following results:
Mean Value = 547.572 mV Peak to Valley Sine = 0.02935 mV
Peak to Valley/Mean = 53.608 ppm Sine Phase = 41.07 deg = Feb 12
We can say definitely, however, that the current source variation is not caused by the Esaki voltage variation. This comes from four independent arguments-all supporting the same conclusion.
・ First, the Esaki voltage has a large linear component which is not at all reflected in the current source variations. Any back impedance effect would certainly be linear and thus can be ruled out.
![]()
Figure 13. The data corrected for current and temperature fluctuations are plotted here with the uncorrected data plotted 0.005 above it for easy comparison. The corrected data is considerably smoother indicating proper correction function.
![]()
Figure 14. Here we plot the current data and its best-least-squares sinusoidal fit. The fit shows 53.6 ppm peak-to-valley sinusoidal variation peaked at Feb 12.
・ Second, the impedance of a high quality current source is quite high by design, and a feedback of 53.6 ppm/850.5ppm = 6.3% would be unimaginable.
・ Third, the sign is wrong. The current increases when the Esaki voltage goes up.
・ Fourth, the phase is shifted by about one month-actually more consistent with the typical radionuclide oscillations.
For these reasons we conclude that the annual time variations of the current source appear to be an independent effect from the Esaki tunnel diode with the same one year period and a 43 day shifted phase (42 deg).
Given the internal feedback loops inside a stabilized current source, we do not place great significance in the shifted phase of the response, and without a more circuit analysis, we cannot verify the cause. The reason we chose a simple Esaki tunnel diode for this experiment was that it provided an easily analyzed physical model whose response to variations in Planck’s constant would be amplified and straightforward. The small current variations from the current source have been removed from the Esaki data using the calibrated linear response of the Esaki voltage to current variations. Thus the current source variations are a separable annual effect.
3. Conclusions
Radioactive decay rate variations from eight radionuclides measured by German, American and Russian labs show sinusoidally varying decay rates peaking in the Jan-Feb time period with minimum decay rates in the July-August period. Since these decay rate oscillations were seen in both strong and weak decays, the author hypothesized that these annual variations in decay rate were compatible with a gradient in Planck’s parameter h across the Earth’s orbit. Planck’s parameter h was chosen as the key parameter for two reasons: First, because the effect was common to strong and weak decays, which are otherwise quite distinct in their physics. Second because radioactive decay rates are quite sensitive to variations in h due to the tunneling effect through the nuclear barrier.
The author then designed a purely electromagnetic test of variations in h using tunnel diodes―which are also quite sensitive to h. Like the nuclear decays, the electron tunneling has an h in the denominator of the exponent, but it also has an h2 in the numerator of the exponent due to the size of an atom being proportional to h2. Since the thickness of a tunnel diode barrier is measured in atoms, the tunneling exponent should increase with h―the exact opposite of nuclear decay where the tunneling exponent decreases as h increase. Thus the prediction for the E&M tunneling experiment was that it would also show a one year period but be 180 deg out of phase with the nuclear data. This prediction was verified by experiment.
The combined strong and weak decay variations and the E&M tunnel diode current variations are consistent with a variation in h of roughly 29 ppm across the Earth’s orbit. Since other cosmological tests for the fine structure variation (proportional to 1/h) have also shown positive variations of similar magnitude at high statistical significance, we hypothesize that Planck’s parameter may vary in space and time and perhaps by frequency, making it an environmental variable rather than a fundamental constant.