Received 22 December 2015; accepted 26 February 2016; published 29 February 2016
1. Introduction
Let basically describe Newtons Binomial Theorem and Fundamental Theorem of Calculus and some their properties. In elementary algebra, the binomial theorem (or binomial expansion) describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the power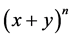 
into a sum involving terms of the form 
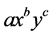where the exponents b and c are nonnegative integers with
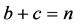, and the coefficient a of each term is a specific positive integer depending on n and b. The coefficient a in the term of 
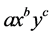is known as the binomial coefficient. The main properties of the binominal theorem are next:
1) The powers of x go down until it reaches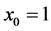 
starting value is n (the n in
).
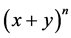2) The powers of y go up from 0 (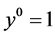
) until it reaches n (also n in
).
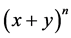3) The n-th row of the Pascal’s Triangle will be the coefficients of the expanded binomial.
4) For each line, the number of products (i.e. the sum of the coefficients) is equal to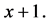 
5) For each line, the number of product groups is equal to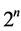
.
By using binomial theorem for our case, we obtain next type function [1] :
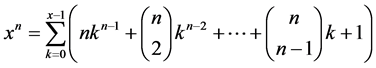
We can reach the same result by using Fundamental Theorem of Calculus, according it we have [2] :
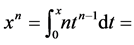
by means of the addition of integrals
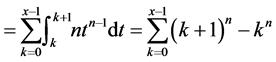
For presented in this paper method, the properties of binomial theorem are not corresponded and prime function (i.e function, which we use with sum operator) has the recursion structure for x basic view is the next: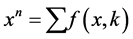
. Below is represented theoretical algorithm deducing such a function, which, when substituted to the sum operator, with some k number of iterations, returns the correct value of a number ![]()
to power![]()
. The main idea that the law for basic elements distribution of the value to third powers seen in finding the n-rank difference (n-rank difference is written as![]()
) between nearest two items![]()
. For example, let there be a set of numbers, which x has constant difference between numbers, constant difference is a key of this method (example for![]()
):
where deltas for ![]()
distribution are equal to:
![]()
going from it we can get next property of the powers function:
![]()
According Table 1 (for case![]()
), the first rank delta has next regularity:
![]()
![]()
![]()
![]()
Note that upper sign shows the rank of the difference and doesn’t mean power sign. As we can see, according Table 1, the values of third rank difference are equal to ![]()
and constant for each i. Going from it, we can to
![]()
Table 1. Numbers according third power.
make conclusion of the next power functions property:![]()
, where ![]()
and constant for each i. For Table 1, the delta functions are corresponding to next expressions:
![]()
where![]()
, hence, we have:
![]()
![]()
Let use sum operator for expression [3] , we obtain [4] :
![]()
Or
![]()
Now, we have successful formula, which disperses any natural number ![]()
to the numerical series (this example shows only expansion for any number ![]()
to third powers, but this method works for floats numbers also, it depends of start set of numbers, functions form also depends of the chosen set, step ![]()
between numbers should be constant every time). Going from it, the next annex shows change over function to the range![]()
.
2. Change over to Higher Powers Expression
In this section are reviewed the ways to change obtained in previous annex expression [4] to higher powers i.e![]()
. By means of Fundamental Theorem of Calculus, we know next [2] :
![]()
Expression [4] has the follow view:
![]()
As we can see, iteration limits for [2] and [4] are:![]()
, for each expression. Consequently, going from [4] , to make the transition to the functions of the form:
![]()
is not possible. Let change the formula [2] by the next way [5] :
![]()
Next, give the formula [2] follow changes:
![]()
Going from expression [5] for ![]()
we obtain [6] :
![]()
By means of main property of the powers function![]()
, from formula [6] for ![]()
we receive [7] :
![]()
According to the above property from the expression [4] for![]()
, we derive [8] :
![]()
For ![]()
expression takes the next form [9] :
![]()
Expression [7] has the next property (as well right for [4] [6] -[8] ):
![]()
3. Binomial Theorem Representation
By means of Binomial theorem for![]()
, we have expression:
![]()
According expression [2] , we have the next corresponding:
![]()
Let, going from expression [4] , change the binomial expansion for![]()
:
![]()
![]()
So, for![]()
, binomial expansion is next:
![]()
oing from it, by means of power function properties, we can only to multiply by x every product of the series, by this way, for ![]()
we have next changes in binomial theorem:
![]()
4. ex Representation
According above method we have right to present function ![]()
the follow view (as the exponential function is the infinite sum of powers of x divided by value of factorial according to iteration step):
![]()
By means of general ![]()
determination, we have right to represent, also, next way:
![]()
5. Difference from Binomial Theorem
To show changes from binomial theorem, let use other algorithm for![]()
, which finally returns the binomial expansion. By means of power functions property:
![]()
We have right to integrate the ![]()
to ![]()
and represent the ![]()
as:
![]()
For third derivative we have next equation:
![]()
Let derive the![]()
:
![]()
Let be![]()
, so we have:
![]()
First derivative is next:
![]()
Let calculate the ![]()
function, basic formula is next:
![]()
And for ![]()
equals to:
![]()
In case of ![]()
we obtain the first derivative:
![]()
So,
![]()
and corresponds to binomial expansion. Main difference is adjustable limits of the function [4] , see page 3 and 4.
6. Conclusion
The paper presented a method of expansion of the function of the form ![]()
to the numerical series. The disadvantages of this method are sophisticated form of expression and the complexity of calculating the value of these expressions of the some variables. Advantage of this method is the possibility of the suc- cessful application of this method in the solution of some problems in number theory, the theory of series, due to the differences from the common theory, displayed the difference from binomial expansion, presented example for exponential function representation by means of method from Section 2. The paper doesn’t consist the all combinations of power function representation (by means of the function [7] property and transformation [5] ). In the Application 1 are shown program codes for the most important expressions (by authors’ opinion). Future research in this direction could result the success polynomial kind expansion.
Application 1. Visual Basic 6.0 Program Codes
Expression [4] :
j = 6 x = Val(Text1.Text) n = Val(Text2.Text) r = 0 For k = 1 To x ![]()
Next k
Expression [6] :
j = 6 x = Val(Text1.Text) n = Val(Text2.Text) r = 0 For k = 1 To x Step 1 For m = 0 To k − 1 Step 1 ![]()
Next m ![]()
Next k
Expression [7] :
j = 6
x = Val(Text1.Text)
n = Val(Text2.Text)
r = 0
For k = 1 To x Step 1
For m = 0 To k − 1 Step 1
![]()
Next m
![]()
Next k
ex Representation:
j = 6
e = 0
x = Val(Text1.Text)
r = Val(Text2.Text)
f = 0
For m = 0 To r Step 1
If m = 0 Then
f = 1
Else
f = f × m
End If
For k = 1 To x
![]()
Next k
Next m