State Price Density Estimation and Nonparametric Pricing of Basket Options

Yuming Kuang, Tze Leung Lai

Department of Statistics, Stanford University, Stanford, CA, USA.

DOI: 10.4236/jmf.2015.55038                

Abstract

This paper develops a novel method to price basket options by using an application-driven approach to estimating the state price density of the basket or the joint state price density of the asset prices in the basket. In this connection, we also discuss the difference between the application-driven and the traditional statistical approach to density estimation.

Keywords

Basket Options, Portfolio Weights, Joint State Price Density

Received 2 October 2015; accepted 27 November 2015; published 30 November 2015

1. Introduction

Basket options are popular derivative contracts. A basket option is an option whose payoff depends on the value of a portfolio (or basket) of n assets which are usually individual stocks or stock indices, currencies or commodities. The value of the portfolio at some future time T is in which 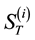is the price of the ith asset and the 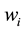is the portfolio weights (possibly negative). Therefore the price of a European call option on the basket, with maturity T and strike price X, is

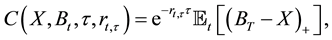(1)

in which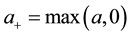, , 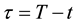denotes conditional expectation, under the risk-neutral measure, given the information set (or more precisely the 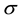-field of events) up to time t, and is the interest rate of a risk-free bond, with maturity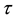, at current time t. Even under the usual assumption that the asset prices 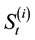follow correlated geometric Brownian motion processes, the computation of (1) involves Monte Carlo simulations, unlike the case 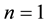for which (1) has an explicit formula, which is the well-known Black-Scholes formula. Therefore, even assuming classical parametric price processes, pricing basket options still undergo recent developments which include analytical approximations and computationally fast upper and lower bounds [1] . In addition, the parametric model involves parameters that have to be estimated from data and this poses new statistical issues. Even for the case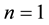, departures from the classical parametric model have manifested themselves in well-documented volatility smiles and skews and have led to more complicated parametric models whose parameters may be much more difficult to estimate and which also exhibit other lack-of-fit patterns.

Hutchinson, Lo and Poggio [2] introduced a nonparametric approach to pricing options, by making the use of basis functions to estimate the pricing function g in the nonparametric regression model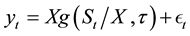, in which 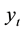denotes the option price and is the additive noise in the regression model. Subsequently, Aït-Sahalia and Lo [3] pointed out that such methods “do not provide any formal statistical inference to gauge the accuracy of these estimators” and introduced a semiparametric approach, which involved semiparametric estimation of the state space density (SPD) and for which they were able to derive an asymptotic sampling theory for statistical inference. Aït-Sahalia and Duarte [4] , Yatchew and Härdle [5] and Yuan [6] provided subsequent improvements in estimating the SPD. We begin Section 2 with a brief review of the main ideas of these methods and then modify them to estimate the SPD of a portfolio of assets, treating the portfolio value as a single combined asset value whose SPD can be estimated from the observed basket option prices. In Section 3, we provide a refinement in nonparametric pricing of a basket option by estimating the joint state price density of using option price data of the n assets. Section 4 gives some concluding remarks and points out in particular how Sections 2 and 3 illustrate a general application-driven approach to estimating densities for financial applications.

2. SPD of a Portfolio and Nonparametric Pricing of Basket Options

2.1. Estimation of SPD of an Asset and Option Pricing

Aït-Sahalia and Lo [3] note that one of the most important advances in the economic theory of investment under uncertainty is the Arrow-Debreu preference-based equilibrium model under which the prices of securities that pay $1 (or nothing) in a specific state of nature (otherwise) are given by the SPD. In particular, in an arbitrage-free options market, the SPD of the price of an asset at some future time T, given the current price S of the asset, can be expressed as the density function with respect to a risk-neutral measure under which is a martingale after multiplication by a stochastic discount factor. The price at time t of a European option on the underlying asset, with maturity T and strike price X, can therefore be expressed in terms of the SPD by

(2)

for a call option, and with replaced by for a put option. Recall that and is the interest rate of a risk-free bond as in (1).

In the classical Black-Scholes model [7] , the underlying asset price process is assumed to follow a geometric Brownian motion under the risk-neutral measure, where W is Brownian motion and denotes the dividend rate. In this model, the SPD belongs to a parametric family (with parameter) of

log-normal distributions as, where is the dividend yield of the

period. Because of well-documented differences between the Black-Scholes and the actual option prices, more flexible (and also more complicated) models have been proposed for the asset price process under the risk-neutral measure, including the implied volatility function (IVF) model, the stochastic volatility (SV) model, and stochastic volatility with contemporaneous jumps in asset prices and volatilities (SVCJ). Aït-Sahalia and Lo [3] therefore propose to use a semiparametric estimator of SPD, which can in turn provide a robust pricing function for European options. Central to their semiparametric approach is the representation of in terms of the second partial derivative of C with respect to X:

(3)

due to Breeden and Litzenberger [8] and Banz and Miller [9] . The semiparametric approach assumes the Black-Scholes pricing function for C but with replaced by a function that is estimated nonparametrically from option price data, where represents the future price of the asset. As a density function, the SPD has to be nonnegative and integrates to 1. The first constraint implies that C is a convex function of X, and the second constraint requires a post-estimate normalization. Aït-Sahalia and Duarte [4] and Yatchew and Härdle [5] propose alternative estimates of C that satisfy the convexity constraints and show their improved accuracy in recovering option prices.

Yuan [6] develops a novel nonparametric estimate of the SPD that can be represented as a nonparametric mixture of log-normal densities. The estimator is defined as the minimizer of the least square criterion applied to the dataset of pairs, , where

(4)

is the pricing function determines by the Black-Scholes call option price and the mixing distribution G of the mean and standard deviation of the normal distribution for. This is a consequence of (2) and the mixture of log-normal densities for. Although the minimization is taken over an infinite-dimensional space of distributions G, Yuan (2009) [6] shows that the minimizing G actually has finite support that consists of at most points. He also reports a simulation study and an empirical analysis of S&P 500 index option prices, showing good performance of the method.

2.2. Nonparametric Pricing of Basket Options via Estimated SPD of Portfolio

Treating the portfolio as an asset, we can follow Yuan’s method described above to estimate the SPD of from a sample of basket option prices and their corresponding strike prices and thereby to obtain a nonparametric pricing function via (4). Specifically, Yuan’s method uses the representation

(5)

where is the density function and when the sample size is M; Yuan’s Theorem 2.1 shows that the minimizer of the least square criterion actually choses when it is assumed that. Although this means that we can choose any, we propose to choose it by cross-validation in practice. We summarize the procedure in the following.

Example 1. Consider, and a portfolio of assets, with weight vector or. The interest rate over the period is assumed to be. The asset prices are assumed to follow correlated geometric Brownian motions under the risk-neutral measure so that has a multivariate normal distribution with mean and covariance matrix

where is trivariate normal with mean and covariance matrix

Here and in the sequel, we use to denote. Conditional on

, the strike price of the basket option is assumed to be. We simulate basket option prices (calls) from this model and use them as data to compute via Algorithm 1 (with and being the range of the 500 portfolio values and the strike prices of the corresponding basket options) the SPD estimate, which is then used to estimate the pricing function by . We also simulate an additional 100 basket calls from this model and compare them with the values obtained by the estimated pricing function. Figure 1 and Figure 2 give the re-

Figure 1. Basket option price (left) and SPD (right) for.

Figure 2. Basket option price (left) and SPD (right) for.

sults comparing these prices, and also the estimated SPD with the actual density function, for and respectively. They show that Algorithm 1 provides excellent estimates of the pricing function and the SPD, for long-only and long-short portfolios.

2.3. Discussion and Related Literature

The approach to density estimation in this section starts with the application at hand to come up with a representation of the density function. In particular, the choice of Gaussian mixture for the SPD in Yuan (2009) [6] is based on the closed-form expression of the option price when is a mixture of Gaussian random variables. Moreover, the criterion used to choose the parameters of the Gaussian mixture (or more general smoothing parameters when other representations of the density function are used) is based on how well the pricing formula approximate the actual option prices as in Algorithm 1 (or on how well the estimated density works for the application at hand), and not on statistical measures such as integrated mean squared error. Moreover, the data used to estimate the density f function need not be samples drawn from f, but can be financial quantities such as option prices that are related to f via the underlying economic theory.

In the statistics literature, the use of Gaussian mixture to estimate density function has been studied from the Bayesian perspective that the weight and parameters of each mixture come from some prior distribution. Suppose the data are conditionally independent and normally distributed, , where the mean and standard deviation is determined by. comes from some prior distribution. Ferguson [10] and Escobar and West [11] consider this mixture model assuming the prior distribution for parameters is Dirichlet process. As a comparison with the kernel density estimator, they pointed out that this model automatically provides a Bayesian decision for the number of mixtures in the density, which leverages the local clustering structure of data points and estimating local structure using combining information. Also by allowing distinct variance in the mixtures, the model is able to apply different smoothing degree to the sample space. As for the estimation of the mixture models, Ferguson [10] proves that the posterior density estimation is to evaluate the ratio of two n-dimensional integrals and suggests Monte Carlo simulation for computation. Kuo [12] proposes an importance sampling Monte Carlo methods to improve the computation efficiency. And Escobar and West [11] suggest a Gibbs sampling methods for parameter estimation by giving the conditional density and then the density estimation can be evaluated by a mixture of Gaussian determined by the estimated’s and prior. They also illustrate the relationship of the parameter in the underlying Dirichlet process and number of mixtures in the density and discussed learning from the data.

3. Estimation of Joint State Price Density and Pricing Function of Basket Options

Using observed basket option prices to estimate the SPD of the underlying portfolio is unrealistic in practice because basket option is exotic options in over-the-counter markets. In fact, financial engineers make use of data from vanilla options on the underlying assets of the basket to price these exotics. We now describe how the method in Section 2.2 can be modified to estimate the joint SPD of the vector from the observed option prices, , , of the underlying assets in the basket and the corresponding asset returns. A natural extension of (5) (with) is

(6)

where denotes the multivariate density function. Note that for the Gaussian mixture model (6),

(7)

The marginal SPD of can be estimated from the option prices, , by using Yuan’s method that yields a mixture normal density, with components densities that have cor-

responding weights . The choice of, and in the estimate of the joint density (5) should yield as the associated marginal density of . This suggests choosing components in the Gaussian mixture and labeling each component as so that

and. It remains to choose. The correlation matrix of can

be estimated from historical returns data since the time series of returns are i.i.d random variables in the Gaussian mixture model [6] , yielding a consistent estimate of. Note that the diagonal elements of the right-hand side of (7) (and of) are already determined by the marginal densities. Making use of these diagonal elements together with and (7), we can then estimate the off-diagonal elements of. Details are given in the following.

Example 2. To illustrate Algorithm 2, this example considers, and portfolio of assets with weight vector. The asset prices are assumed to follow correlated geometric Brownian motions with random volatilities, and instantaneous correlation coefficient that are independently

generated from truncated normal distributions:, , , in which denotes truncation to stay inside A. Similar to Example 1, we sample, and the strike price for the basket is, which those for the two assets are,

. We simulate 300 call option prices for each asset and use them as data to compute via

Algorithm 1 (for the 300 calls) the SPD and. In addition, 1000 asset returns for each asset are also generated so that Algorithm 2 can be applied to compute basket option prices for comparison with 100 basket option prices generates for out-of-sample testing of the performance of Algorithm 2. The left hand side of Figure 3 and Figure 4 provide the result of estimated option price surface using joint state price density estimation for case and. The x- and y-axis are the asset current prices adjusted by basket option strike and z-axis is the option price adjusted by basket option strike. Also on the right hand side we provide the box plot of the residual between estimated and observed option prices adjusted by the strike price. Clearly the estimated option price surface using Algorithm 2 captures the observed option prices.

Figure 3. Basket option price using joint state price density for (left); box plot for residual between estimated and observed option price (right).

Figure 4. Basket option price using joint state price density for (left); box plot for residual between estimated and observed option price (right).

Estimating the joint SPD in this section seems to be much easier than estimating the joint density of a multivariate distribution in the statistics. It starts by estimating the marginal density of each component of the random vector and then combines them via an estimated correlation matrix in the Gaussian mixture model (6). For multivariate kernel estimators in the statistics literature (see reviews by Scott and Sain [13] and Hwang, Lay and Lippman [14] ), choosing smoothing parameters means choosing a transformation matrix H, in particular the Gaussian kernel becomes, where. The simplest choice is, which means using no rotation and a global bandwidth h. A slightly more general choice suggested by Sain, Beggarly and Scott [15] is a diagonal matrix for H, which is tantamount to choosing different bandwidths for different coordinates. It has been found that using a predetermined H may give poor estimates of the joint density and methods to estimate H from the data by cross-validation or plug-in have been proposed [16] . These methods have been shown to work well when the dimension n is small, but suffer the `curse of dimensionality’ in both accuracy and computation time for larger n.

4. Conclusion

The approach used in Sections 2 and 3 to estimate a density function (specifically the SPD) exemplifies an application-driven density estimation methodology that has major differences from traditional density estimators in the statistics literature. Traditional density estimators use kernels of the form, in which and denote the observations sampled from a population with density f, or use basis functions such as log-splines to approximate f so that the coefficients associated with the basis functions can be estimated from the data. A central question is a choice of the smoothing parameters. For univariate () kernel density estimators, an optimal choice of the smoothing parameter h is based on the integrated mean squared

error (IMSE), which can be asymptotically approximated the asymptotic integrated squared error

(8)

where. The asymptotically optimal bandwidth to minimize AISE is

(9)

but it cannot be implemented because is unknown. Three classes of methods have been developed to overcome this difficulty: 1) assuming a parametric family for f so that can be determined from the density associated with the optimal parameter; 2) cross-validation, which uses leave-one-out or k-fold cross-validation to pick the optimal bandwidth; 3) finding the optimal bandwidth for the problem of estimating with a kernel estimator and then plugging the estimated into (9). As reviewed in the last paragraph of Section 3, extension of this idea to this case should involve replacing h by a transformation matrix H, which may perform considerably better than the traditional choice. However, this is actually irrelevant to the particular application of estimating the SPD because the data having this joint density under the risk-neutral measure are not directly observable; the observed data in Section 3 are the option prices and the asset returns instead.

Acknowledgements

This research is supported by the National Science Foundation grant DMS 1407828.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Caldana, R., Fusai, G., Gnoatto, A. and Grasselli, M. (2014) General Closed-Form Basket Option Pricing Bounds. Available at SSRN 2376134.
[2]	Hutchinson, J.M., Lo, A.W. and Poggio, T. (1994) A Nonparametric Approach to Pricing and Hedging Derivative Securities via Learning Networks. Journal of Finance, 49, 851-889. http://dx.doi.org/10.1111/j.1540-6261.1994.tb00081.x
[3]	Aït-Sahalia, Y. and Lo, A.W. (1998) Nonparametric Estimation of State-Price Densities Implicit in Financial Asset Prices. Journal of Finance, 53, 499-547. http://dx.doi.org/10.1111/0022-1082.215228
[4]	Aït-Sahalia, Y. and Duarte, J. (2003) Nonparametric Option Pricing under Shape Restrictions. Journal of Econometrics, 116, 9-47. http://dx.doi.org/10.1016/S0304-4076(03)00102-7
[5]	Härdle, W. and Yatchew, A. (2001) Dynamic Nonparametric State Price Density Estimation Using Constrained Least Squares and the Bootstrap. Discussion Papers, Interdisciplinary Research Project 373: Quantification and Simulation of Economic Processes No. 2002, 16.
[6]	Yuan, M. (2009) State Price Density Estimation via Nonparametric Mixtures. Annals of Applied Statistics, 3, 963-984. http://dx.doi.org/10.1214/09-AOAS246
[7]	Black, F. and Scholes, M. (1973) The Pricing of Options and Corporate Liabilities. The Journal of Political Economy, 81, 637-654. http://dx.doi.org/10.1086/260062
[8]	Breeden, D.T. and Litzenberger, R.H. (1978) Prices of State-Contingent Claims Implicit in Option Prices. Journal of Business, 51, 621-651. http://dx.doi.org/10.1086/296025
[9]	Banz, R.W. and Miller, M.H. (1978) Prices for State-Contingent Claims: Some Estimates and Applications. Journal of Business, 51, 653-672. http://dx.doi.org/10.1086/296026
[10]	Ferguson, T.S. (1983) Bayesian Density Estimation by Mixtures of Normal Distributions. Recent Advances in Statistics, 24, 287-302.
[11]	Escobar, M.D. and West, M. (1995) Bayesian Density Estimation and Inference Using Mixtures. Journal of the American Statistical Association, 90, 577-588. http://dx.doi.org/10.1080/01621459.1995.10476550
[12]	Kuo, L. (1986) Computations of Mixtures of Dirichlet Processes. SIAM Journal on Scientific and Statistical Computing, 7, 60-71. http://dx.doi.org/10.1137/0907004
[13]	Scott, D.W. and Sain, S.R. (2005) Multidimensional Density Estimation. In: Rao, C.R., Ed., Handbook of Statistics Elvesier, New York, 229-261. http://dx.doi.org/10.1016/s0169-7161(04)24009-3
[14]	Hwang, J.N., Lay, S.R. and Lippman, A. (1994) Nonparametric Multivariate Density Estimation: A Comparative Study. IEEE Transactions on Signal Processing, 42, 2795-2810. http://dx.doi.org/10.1109/78.324744
[15]	Sian, S.R., Baggerly, K.A. and Scott, D.W. (1994) Cross-Validation of Multivariate Densities. Journal of American Statistical Association, 89, 807-817. http://dx.doi.org/10.1080/01621459.1994.10476814
[16]	Duong, T. (2007) ks: Kernel Density Estimation and Kernel Discriminant Analysis for Multivariate Data in R. Journal of Statistical Software, 21, 1-16. http://dx.doi.org/10.18637/jss.v021.i07