Matrix Inequalities for the Fan Product and the Hadamard Product of Matrices

Dongjie Gao^*

Department of Mathematics, Heze University, Heze, China.

DOI: 10.4236/alamt.2015.53009                

Abstract

A new inequality on the minimum eigenvalue for the Fan product of nonsingular M-matrices is given. In addition, a new inequality on the spectral radius of the Hadamard product of nonnegative matrices is also obtained. These inequalities can improve considerably some previous results.

Keywords

M-Matrix, Nonnegative Matrix, Fan Product, Hadamard Product, Spectral Radius, Minimum Eigenvalue

1. Introduction

Let, and. We write 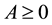if 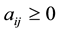for any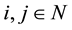. If, A is called a nonnegative matrix, and if A > 0, A is called a positive matrix. The spectral radius of a nonnegative matrix A is denoted by.

We denote by Z_n the class of all n × n real matrices, all of whose off-diagonal entries are nonpositive. A matrix 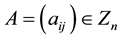is called an M-matrix if there exists a nonnegative matrix B and a nonnegative real number s, such that 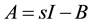with, where I is the identity matrix. If 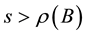(resp.,), then the M-matrix A is nonsingular (resp., singular) (see [1] [2] ). Denote by M_n the set of nonsingular M-matrices. We define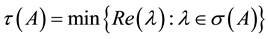, where 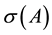denotes the spectrum of A.

The Fan product of two matrices and is the matrix, where

If, then so is. In ([2] , p. 359), a lower bound for was given: if, then.

If, and, we write, where. Thus we define. Obviously, J_A is nonnegative. Recently, some authors gave some lower bounds of (see [3] -[8] ). In [4] , Huang obtained the following result for,

(1)

The bound of (1) is better than the bound in ([2] , p. 359).

In [7] , Liu gave a lower bound of,

(2)

where. The bound of (2) is better than the one of (1).

For a nonnegative matrix, let, where. We denote, where,

The Hadamard product of two matrices and is the matrix . For two nonnegative matrices A and B, recently, some authors gave several new upper bounds of (see [3] -[7] [9] ). In [4] , Huang obtained the following result for,

1) If, then

(3)

2) If or for some i₀, but, then

(4)

3) If and, then

(5)

4) If and for some i₀, j₀, then the upper bound of is the maximum value of the upper bounds of the inequalities in (3)-(5).

The bound of in [4] is better than that in ([2] , p. 358).

In [7] , Liu gave a new upper bound of,

1) If, then

(6)

where.

2) If and or and for some, but, then

(7)

3) If and, then

(8)

4) If and for some i₀, j₀, then the upper bound of is the maximum value of the upper bounds of the inequalities in (6)-(8).

The bound of in [7] is better than that in [4] .

The paper is organized as follows. In Section 2, we give a new lower bound of. In Section 3, we present a new upper bound of.

2. Inequalities for the Fan Product of Two M-Matrices

In this section, we will give a new lower bound of.

If and, we write for the k-th Hadamard power of A. If and, we write.

Lemma 1. [7] Let, and let be two positive diagonal matrices. Then

Lemma 2. [2] If is a nonnegative matrix and, then

Theorem 1. Let and. Then

where.

It is evident that the Theorem holds with equality for n = 1. Next, we assume that.

(1) First, we assume that is irreducible matrix, then A and B are irreducible. Obviously J_A and J_B are also irreducible and nonnegative, so and are nonnegative irreducible matrices. Then there exist two

positive vectors and such that and. Let

Then we have and, that is

Let and in which U and V are the nonsingular diagonal matrices

and. Then, we have

It is easy to see that, , and VU are nonsingular since V and U are. From Lemma 1, we have

Thus, we obtain, and

We next consider the minimum eigenvalue of. Let. Then we have that. By Theorem 1.23 of [10] , there exist, , such that

By Hölder’s inequality, we have

Then, we have

Since, then

Hence,

i.e.,

(2) Now, assume that is reducible. It is well known that a matrix in Z_n is a nonsingular M-matrix if and only if all its leading principal minors are positive (see [11] ). If we denote by the n × n permutation matrix with, the remaining t_ij zero, then both and are irreducible nonsingular M-matrix for any chosen positive real number, sufficiently small such that all the leading principal minors of both and are positive. Now, we substitute and for A and B, respectively, in the previous case, and then letting, the result follows by continuity.

Remark 1. By Lemma 2, the bound in Theorem 1 is better than that in Theorem 4 of [8] and Theorem 2 of [7] .

Example 1. Let

By calculating with Matlab 7.1, it is easy to show that.

Applying Theorem 4 of [4] , Theorem 3.1 of [5] , Theorem 2 of [7] , and Theorem 3.1 of [8] , we have, , , and, respectively. But, if we apply Theorem 1, we have

The numerical example shows that the bound in Theorem 1 is better than that in Theorem 4 of [4] , Theorem 3.1 of [5] , Theorem 2 of [7] , and Theorem 3.1 of [8] .

3. Inequalities for the Hadamard Product of Two Nonnegative Matrices

In this section, we will give a new upper bound of for nonnegative matrices A and B. Similar to [7] , for, write Q = A − D, where. We denote with, where

Note that is nonnegative, and if,. For, let, where

Similarly, the nonnegative matrix is defined.

Lemma 3. [2] Let, and let be diagonal matrices. Then

Lemma 4. [12] Let be a nonnegative matrix. Then

Theorem 2. Let, and. Then

1) If, then

(9)

where.

2) If and or and for some, but, then

(10)

3) If and, then

(11)

4) If and for some i₀, j₀, then the upper bound of is the maximum value of the upper bounds of the inequalities in (9)-(11).

Proof. It is evident that 4) holds with equality for n = 1. Next, we assume that.

(1) First, we assume that is irreducible matrix, then A and B are irreducible. Obviously and are also irreducible and nonnegative, so and are nonnegative irreducible matrices. Then there exist two positive vectors and such that and. Let

Then we have and, that is

Let and in which U and V are the nonsingular diagonal matrices

and. Then we have

It is easy to see that, , and VU are nonsingular since V and U are. From Lemma 4, we have

Thus, we obtain, and

We next consider the minimum eigenvalue of. For nonnegative irreducible matrices

and, by definition of the Hadamard product of and, Hölder’s inequality, and Lemma 5, we have

Thus, we obtain

1) If, then

2) If and or and for some i₀, j₀, but, then

3) If and, then

4) If and for some i₀, j₀, then the upper bound of is the maximum value of the upper bounds of the inequalities in (9)-(11).

(2) Now, we assume that is reducible. If we denote by the n × n permutation matrix with, the remaining t_ij = 0, then both and are irreducible nonsingular matrices for any chosen positive real number. Now, we substitute and for A and B, respectively, in the previous case, and then letting, the result follows by continuity.

Remark 2. By Lemma 2, the bound in Theorem 2 is better than that in Theorem 6 of [6] and Theorem 3 of [9] .

Example 2. Let

By calculation with Matlab 7.1, we have, , , , and.

If we apply Theorem 6 of [4] , Theorem 3 of [7] , and Theorem 2.2 of [9] , we have, , and, respectively. But, if we apply Theorem 2, we have

The numerical example shows that the bound in Theorem 2 is better than that in Theorem 6 of [4] , Theorem 3 of [7] , and Theorem 2.2 of [9] .

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Berman, A. and Plemmons, R.J. (1979) Nonnegaive Matrices in the Mathematical Sciences. Academic Press, New York.
[2]	Horn, R.A. and Johnson, C.R. (1985) Topics in Matrix Analysis. Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9780511810817
[3]	Fang, M.Z. (2007) Bounds on Eigenvalues for the Hadamard Product and the Fan Product of Matrices. Linear Algebra and its Applications, 425, 7-15. http://dx.doi.org/10.1016/j.laa.2007.03.024
[4]	Huang, R. (2008) Some Inequalities for the Hadamard Product and the Fan Product of Matrices. Linear Algebra and its Applications, 428, 1551-1559. http://dx.doi.org/10.1016/j.laa.2007.10.001
[5]	Li, Y.T., Li, Y.Y., Wang, R.W. and Wang, Y.Q. (2010) Some New Lower Bounds on Eigenvalues of the Hadamard Product and the Fan Product of Matrices. Linear Algebra and its Applications, 432, 536-545. http://dx.doi.org/10.1016/j.laa.2009.08.036
[6]	Liu, Q.B. and Chen, G.L. (2009) On Two Inequalities for the Hadamard Product and the Fan Product of Matrices. Linear Algebra and its Applications, 431, 974-984. http://dx.doi.org/10.1016/j.laa.2009.03.049
[7]	Liu, Q.B., Chen, G.L. and Zhao, L.L. (2010) Some New Bounds on the Spectral Radius of Matrices. Linear Algebra and its Applications, 432, 936-948. http://dx.doi.org/10.1016/j.laa.2009.10.006
[8]	Zhou, D.M., Chen, G.L., Wu, G.X. and Zhang, X.Y. (2013) On Some New Bounds for Eigenvalues of the Hadamard Product and the Fan Product of Matrices. Linear Algebra and its Applications, 438, 1415-1426. http://dx.doi.org/10.1016/j.laa.2012.09.013
[9]	Zhao, L.L. (2012) Two Inequalities for the Hadamard Product of Matrices. Journal of Inequalities and Applications, 2012, 1-7. http://dx.doi.org/10.1186/1029-242X-2012-122
[10]	Varga, R.S. (1962) Matrix Iterative Analysis. Prentice-Hall, Englewood Cliffs.
[11]	Berman, A. and Plemmons, R.J. (1994) Nonnegaive Matrices in the Mathematical Sciences. SIAM, Philadelphia. http://dx.doi.org/10.1137/1.9781611971262
[12]	Brauer, A. (1947) Limits for the Characteristic Roots of a Matrix Ⅱ. Duke Mathematical Journal, 14, 21-26. http://dx.doi.org/10.1215/S0012-7094-47-01403-8