The Global Attractors for a Nonlinear Viscoelastic Wave Equation with Strong Damping and Linear Damping and Source Terms ()
1. Introduction
We know that viscoelastic materials have memory effects. These properties are due to the mechanical response influenced by the history of the materials. As these materials have a wide application in the natural science, their dynamics are of great importance and interest. The memory effects can be modeled by a partial differential equation. In recent years, the behaviors of solutions for the PDE system have been studied extensively, and many achievements have been obtained. Many authors have focused on the problem of existence, decay and blow-up for the last two decades, see [1] -[5] . And the attractors are still important contents that are studied.
In [6] , R.O. Araújo, T. Ma and Y.M. Qin studied the following equation
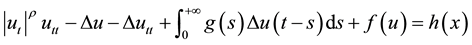 (1.1)
(1.1)
and they proved the global existence, uniqueness and exponential stability of solutions and existence of the global attractor.
In [7] , Y.M. Qin, B.W. Feng and M. Zhang considered the following initial-boundary value problem:
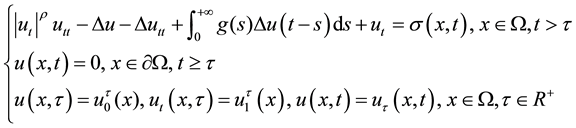 (1.2)
(1.2)
where 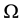 is a bounded domain of
is a bounded domain of  with a smooth boundary
with a smooth boundary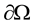 ,
, 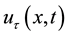 (the past history of u) is a given datum which has to be known for all
(the past history of u) is a given datum which has to be known for all , the function g represents the kernel of a memory,
, the function g represents the kernel of a memory, 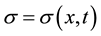
is a non-autonomous term, called a symbol, and ρ is a real number such that 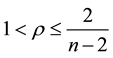 if
if ;
; 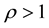 if
if
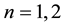 . They proved the existence of uniform attractors for a non-autonomous viscoelastic equation with a past history. For more related results, we refer the reader to [8] -[14] .
. They proved the existence of uniform attractors for a non-autonomous viscoelastic equation with a past history. For more related results, we refer the reader to [8] -[14] .
In this work, we intend to study the following initial-boundary problem:
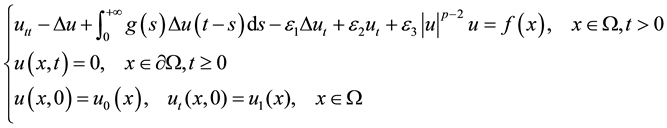 (1.3)
(1.3)
where  and
and 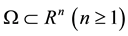 is a bounded domain with smooth boundary
is a bounded domain with smooth boundary ,
,
![]() if
if![]() ;
; ![]() if
if![]() , for the problem (1.3), the memory term
, for the problem (1.3), the memory term
![]() replaces
replaces![]() , and we consider the strong damping term
, and we consider the strong damping term![]() , the li-
, the li-
near damping term ![]() and source terms
and source terms![]() . We define
. We define
![]()
A direct computation yields
![]()
Thus, the original memory term can be written as
![]()
and we get a new system
![]() (1.4)
(1.4)
![]() (1.5)
(1.5)
with the initial conditions
![]() (1.6)
(1.6)
and the boundary conditions
![]() (1.7)
(1.7)
The rest of this paper is organized as follows. In Section 2, we first obtain the priori estimates, then in Section 3, we prove the existence of the global attractors.
For convenience, we denote the norm and scalar product in ![]() by
by ![]() and
and![]() , let
, let![]() ,
,![]() .
.
2. The Priori Estimates of Solution of Equation
In this section, we present some materials needed in the proof of our results, state a global existence result, and prove our main result. For this reason, we assume that
(G1) ![]() is a differentiable function satisfying
is a differentiable function satisfying![]() ;
;
(G2)![]() ;
;
(G3) There exists a constant ![]() such that
such that![]() ,
,![]() ;
;
Lemma 1. Assume (G1), (G2) and (G3) hold, let
![]()
and![]() ,
, ![]() ,
, ![]() , then the solution
, then the solution ![]() of Equation (1.3) satisfies
of Equation (1.3) satisfies
![]() and
and
![]() (2.1)
(2.1)
here![]() , thus there exists
, thus there exists ![]() and
and![]() , such that
, such that
![]() (2.2)
(2.2)
Proof. We multiply ![]() with both sides of equation and obtain
with both sides of equation and obtain
![]()
By using Holder inequality, Young’s inequality and Poincare inequality, we get
![]() (2.3)
(2.3)
and
![]() (2.4)
(2.4)
and
![]() (2.5)
(2.5)
For the first term on the right side (2.5), by using (G1), (G2) and (G3), we have
![]() (2.6)
(2.6)
where
![]() (2.7)
(2.7)
For the second term on the right side (2.5), by using Holder inequality and Young’s inequality, we get
![]() (2.8)
(2.8)
So, we have
![]() (2.9)
(2.9)
By using Poincare inequality, we obtain
![]() (2.10)
(2.10)
and
![]() (2.11)
(2.11)
and
![]() (2.12)
(2.12)
By using Holder inequality and Young’s inequality, we obtain
![]() (2.13)
(2.13)
Then, we have
![]() (2.14)
(2.14)
That is
![]() (2.15)
(2.15)
Next, we take proper![]() , such that
, such that
![]() (2.16)
(2.16)
Taking![]() , then
, then
![]() (2.17)
(2.17)
where![]() , by using Gronwall inequality, we obtain
, by using Gronwall inequality, we obtain
![]() (2.18)
(2.18)
From![]() , according to Embedding Theorem then
, according to Embedding Theorem then![]() , let
, let![]() , so we have
, so we have
![]()
Then
![]()
So, there exists ![]() and
and![]() , such that
, such that
![]()
Lemma 2. Assume (G1), (G2) and (G3) hold, let
![]()
and![]() ,
, ![]() ,
, ![]() , then the solution
, then the solution ![]() of Equation (1.3) satisfies
of Equation (1.3) satisfies ![]() and
and
![]() (2.19)
(2.19)
Here![]() , thus there exists
, thus there exists ![]() and
and![]() , such that
, such that
![]() (2.20)
(2.20)
Proof. We multiply ![]() with both sides of equation and obtain
with both sides of equation and obtain
![]() (2.21)
(2.21)
By using Holder inequality, Young’s inequality and Poincare inequality, we get
![]()
and
![]() (2.22)
(2.22)
and
![]() (2.23)
(2.23)
For the first term on the right side (2.23), by using (G1), (G2) and (G3), we have
![]() (2.24)
(2.24)
where
![]() (2.25)
(2.25)
For the second term on the right side (2.23), by using Holder inequality and Young’s inequality, we get
![]() (2.26)
(2.26)
so, we have
![]()
By using Poincare inequality, we have
![]() (2.27)
(2.27)
and
![]() (2.28)
(2.28)
And using Interpolation Theorem, we have
![]() (2.29)
(2.29)
By using Holder inequality and Young’s inequality, we have
![]() (2.30)
(2.30)
Then, we have
![]()
That is
![]() (2.31)
(2.31)
Next, we take proper![]() , such that
, such that
![]() (2.32)
(2.32)
Taking![]() , then
, then
![]() (2.33)
(2.33)
where![]() , by Gronwall inequality, we have
, by Gronwall inequality, we have
![]() (2.34)
(2.34)
From![]() , according to Embedding Theorem, then
, according to Embedding Theorem, then![]() , let
, let![]() , so, we have
, so, we have
![]()
then
![]()
So, there exists ![]() and
and![]() , such that
, such that
![]()
3. Global Attractors
Theorem 1. Assume (G1), (G2) and (G3) hold, let
![]()
and![]() ,
, ![]() ,
, ![]() , so Equation (1.3) exists a unique smooth solution
, so Equation (1.3) exists a unique smooth solution
![]()
Proof. By the method of Galerkin and Lemma 1 and Lemma 2, we can easily obtain the existence of solutions. Next, we prove the uniqueness of solutions in detail.
Assume that ![]() are two solutions of equation, let
are two solutions of equation, let![]() , then, the two equations subtract and obtain
, then, the two equations subtract and obtain
![]() (3.1)
(3.1)
where
![]() (3.2)
(3.2)
By multiplying the equation by ![]() and integrating over
and integrating over![]() , we get
, we get
![]() (3.3)
(3.3)
here
![]() (3.4)
(3.4)
and
![]() (3.5)
(3.5)
by using (G1), (G2) and (G3), we have
![]() (3.6)
(3.6)
By using Poincare inequality, we have
![]() (3.7)
(3.7)
and
![]() (3.8)
(3.8)
By using Holder inequality, Young’s inequality and Poincare inequality, we have
![]() (3.9)
(3.9)
then, we have
![]() (3.10)
(3.10)
That is
![]() (3.11)
(3.11)
Taking![]() , then
, then
![]() (3.12)
(3.12)
By using Gronwall inequality, we have
![]() (3.13)
(3.13)
So we get![]() , the uniqueness is proved.
, the uniqueness is proved.
Theorem 2. Let X be a Banach space, and ![]() are the semigroup operator on X.
are the semigroup operator on X.![]() ,
, ![]() ,
, ![]() , here I is a unit operator. Set
, here I is a unit operator. Set ![]() satisfy the follow conditions.
satisfy the follow conditions.
1) ![]() is bounded, namely
is bounded, namely![]() ,
, ![]() , it exists a constant
, it exists a constant![]() , so that
, so that
![]()
2) It exists a bounded absorbing set![]() , namely,
, namely, ![]() , it exists a constant
, it exists a constant![]() , so that
, so that
![]()
3) When![]() ,
, ![]() is a completely continuous operator A.
is a completely continuous operator A.
Therefore, the semigroup operators ![]() exist a compact global attractor.
exist a compact global attractor.
Theorem 3. Under the assume of Theorem 1, equations have global attractor
![]()
where![]() ,
, ![]() is the bounded absorbing set of
is the bounded absorbing set of
![]() and satisfies
and satisfies
1)![]() ,
,![]() ;
;
2)![]() , here
, here ![]() and it is a bounded set,
and it is a bounded set,
![]()
Proof. Under the conditions of Theorem 1, it exists the solution semigroup![]() , here
, here![]() ,
,![]() .
.
1) From Lemma 1 to Lemma 2, we can get that ![]() is a bounded set that includes in
is a bounded set that includes in
the ball![]() ,
,
![]()
This shows that ![]() is uniformly bounded in
is uniformly bounded in![]() .
.
2) Furthermore, for any![]() , when
, when![]() , we have
, we have
![]()
So, we get ![]() is the bounded absorbing set.
is the bounded absorbing set.
3) Since ![]() is tightly embedded, which means that the bounded set in
is tightly embedded, which means that the bounded set in ![]() is the tight set in
is the tight set in![]() , so the semigroup operator
, so the semigroup operator ![]() is completely continuous.
is completely continuous.
So, the semigroup operators ![]() exist a compact global attractor A. The proof is completed.
exist a compact global attractor A. The proof is completed.
Acknowledgements
The authors express their sincere thanks to the anonymous reviewer for his/her careful reading of the paper, giving valuable comments and suggestions. These contributions greatly improved the paper.
Funding
This work is supported by the National Natural Sciences Foundation of People’s Republic of China under Grant 11161057.