Natural Oscillations of Cylindrical Bodies with External Friction on the Boundary

Safarov Ismail Ibrahimovich, Akhmedov Maqsud Sharipovich, Boltaev Zafar Ihterovich

Bukhara Engineering-Technological Institute, Bukhara, Republic of Uzbekistan.

DOI: 10.4236/am.2015.63057                

Abstract

In this paper we consider of natural oscillations cylindrical bodies with external friction. Complex rates changes from friction parameters are shown. Rate equations are solved numerically—by method of Muller.

Keywords

External Friction, The Natural Oscillations, Cylindrical Body, Flat Swing, Ant Plane Oscillation Frequency, Damping Factor

1. Introduction

Simulation of vibrations of bodies located in the deformable medium is studied with many scientists and by various methods [1] -[4] . Study of dynamic stress-strain state of pipelines in soil medium, refers to the complex task of solid mechanics. In some researches [5] [6] deformable surrounding in the pipe replaced by springs and considered as emerging (linear and nonlinear) reducing force. In this paper, vibrations of pipelines as a cylindrical body with radiuses r₀ and R at deformable surroundings are modeled (Figure 1). Medium was replaced with viscous damping in the radial and tangential direction. The main aim of the work is to study the oscillations of a cylinder with external friction on the edge and to compare the results of the body located in an elastic medium [3] .

2. Statement of the Problem

Study fluctuations pipeline located in an elastic medium are considered different methods [6] - [9] .

In this paper, fluctuations pipelines are modeled as a cylindrical body with a radius 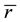and R, located in a deformable medium (Figure 1). Medium was replaced with viscous damping in the radial and tangential direc-

Figure 1. Design model of cylindrical bodies with a viscous external friction.

tion. The main goal of the work is to study the natural oscillations a cylinder with external friction. In the study mentioned above, the optimal values of damping coefficients, in which the oscillations are, damped pipelines as possible.

Consider the problem of the oscillations of an infinite elastic cylinder with external friction at the interface (Figure 2). Closed system of equations of small oscillations of the free elastic cylindrical body has the form:

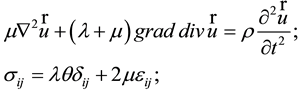(1)

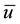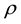where―displacement vector;―lame coefficients;―the density of the cylinder;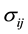―the stress tensor;―strain tensor. On the part of the boundary 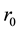given movement: 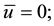apart R-Voltage: 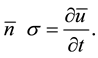As well as the initial conditions:

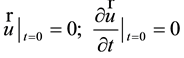
Consider the problem in cylindrical coordinates 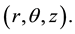Assuming that z coordinate does not affect the oscil- lation, we obtain a system of equations splits into two independent tasks [7] :

(2а)

(2b)

(a)(b)

Figure 2. (a) The dependence of the real part of the eigenvalues of α (n = 0); (b) The dependence of the imaginary part of the eigenvalues of α (n = 0).

With boundary conditions:

at:

(2с)

where R-radius of the cylinder; -parameters of friction at

(2d)

Then we call the boundary value problem (2a)-ant plane and (2b)-flat or planar problem of oscillations of a cylinder.

3. Methods for Solving the Problem of Natural Oscillations

We call the natural oscillations of an elastic cylinder solution of (2a) and (2d) (f = 0) for ant plane case types:

(3a)

problem (2b and 2d) for the planar case types:

(3b)

where -unknown function of the radial vibration modes; -complex natural frequency of the cylinder, the real part of which characterizes the frequency of oscillation of the cylinder, and the imaginary part―the rate of decay, [8] . Substituting the representation (3a), (3b) in Equations (2a) and (2b) and the boundary conditions (2p), (2q), we obtain the spectral problem for the (two) ordinary differential equations solved for the first derivatives of the radial coordinate r: For the case of plane vibrations

(4а)

Ant planar

(4b)

It can be shown that the conditions for the finiteness of all the unknowns in the center for a solid cylinder equivalent to the following boundary conditions-for flat cylinder oscillation:

At n > 1 can be set equal to zero any set of two unknowns. Indeed, if the conditions of the limb in the center of the cylinder, then can be represented as:

(5а)

where―unknown coefficients.

Then substituting (5a) to (4a) we obtain a system of four equations. Equating them coefficients of like powers of r we obtain the recurrence relation:

At we find that for n = 0―finite, tend to zero; at n = 1―finite,―tend to zero; for n > 1 tend to zero all unknown.

If ant planar cylinder oscillation: the n = 0 at n = 1:, at n > 1 either of the two unknowns can be set equal to zero. Indeed, if the conditions of the limb in the center of the cylinder at the time:

(5b)

where―unknown coefficients.

Substituting (5b) in (4b), we obtain a system of two equations. Equating them to obtain coefficients of the same recurrence relation:

Then for at n = 0 of course, tend to zero; at n = 1―of course,―tends to zero for n > 1 tend to zero, both unknown.

The general solution of the system of Equations (2a, 2, c) can be expressed in terms of Bessel and Neman functions n―the order:

(6)

where A, B―arbitrary constants;―Bessel function of order n;―Neman function of order n.

When substituting (6) into (2c and 2d), we obtain the characteristic equation for w:

(7)

Theorem. Let the Eigen values boundary value problems

Simple. Then the system where―Eigen functions of the problem (8), corresponding to the eigenvalues, Rises basis in the space [8] .

Proof. To prove the theorem using the definition from [8] . A boundary value problem can be represented as:

(9)

where

―arbitrary polynomials. Then

Definition 1 is the number of order linear for for (9), if the form contains variables or at and contains such variables in. Order boundary condition

will be called the order of the corresponding linear form. Number called a total order of the boundary conditions (9).

Definition 2 will be called the boundary conditions (9) normalized if any n boundary conditions, they are equivalent, i.e., received (9) are linear combinations of not less than the total order. Given the total order of the boundary conditions (9) is called a total order of the boundary conditions, we obtain from (9) after normalization.

Rewrite Equation (8a) and boundary conditions (8b) in the form (9). To make the replacement is necessary, so that the new unknown changed from zero to unity.

We introduce. Equation (8) will become:

(10)

We introduce the coefficients

Boundary conditions:

(11)

c = 1 ? total order.

The characteristic equation for (9) has the form:

(12)

Its roots are denoted substituting the coefficients we obtain:

(13)

If the roots of the characteristic Equation (12) is simple, and the coefficients. Then from [8] that the complex plane can be divided into sectors 2h in each of which Equation (9) has a

fundamental system of solutions where these solutions and their derivatives up to order n ‒ 1 shall be permitted in these sectors asymptotic expansions:

(14)

where and the first expansions-function do not depend on s. In [8] it is also noted that the functions involved in the expansions (14) do not depend on the choice

of sector and the sequence of the system of recurrence equations.

We represent the solution of our problem in the form (14):

,

The eigenvalues of the problem (9), (10) are determined by the zeros of the characteristic determinant which has the form:

Expanding the determinant, we obtain:

where;―arbitrary set of distinct positive integers ranging from 1 to n. For k = 0 we set In this case.

Then

(15)

We introduce the definition of [8] .

Definition 3. Boundary value problem (9), (10) is said to be regular if all the coefficients in Equation (9)―summing functions and numbers in the expansions corresponding corner points different from zero.

Let M denote the smallest convex polygon containing the point our case M-segment. Point that were on the boundary of the polygon M, called a boundary, and the points that lie at the vertices of M-the cor- ner.

Definition 4. Regular boundary value problem is said to be strongly regular if the zeros of the characteristic determinant asymptotically simple and separated from each other by a positive number.

And obtained Equation (9), the coefficients -enterable functions. Hence when иour problem is regular. We show that it is a regular hard task. We find the asymptotic approximation of zeros of the determinant To do this, we introduce the notation. The (15) can by written as:

We assume without loss of generality that Then we denote

The equation becomes:

At there exists a countable set of eigenvalues determined by a multi-valued function of the logarithm:

(16)

Hence the zeros of the characteristic determinant asymptotically simple and separated from each other by a positive their identical real parts and imaginary spaced on. So the problem (8a) and (8b) increasingly regularly. From the corollary of the theorem in [8] for a regular hard task gets basis function

in space

4. The Numerical Results of the Problem of Their Own Ant Planar Oscillations of the Cylinder

The results of calculations are given in dimensionless system of units in which the value of the shear modulus m, density cylinder, radius of the cylinder Requal to one. Poisson's ratio is assumed to by 0.25. In the case of roots of Equation (7) correspond to the natural frequencies of vibration of the free elastic cylinder. For small solution of the characteristic equation was found method of a small parameter, i.e., it was assumed that

(17)

Then, after the stand (17) (7) have:

(18)

where―solution of the problem on their own ant planar oscillations of elastic cylinder with. In the case where cannot be considered “small” parameter, a direct solution of the transcendental characteristic equation is solved by Muller [9] . For small numerical solution coincides with the solution by the method of the small parameter, see Figure 2: dotted line-solution to the problem of the small parameter method of, the solid line-solution to the problem method of Mueller; Figure 2 shows the relationship; Figure 2―the imaginary part numbers are marked on the charts rooms mod. At the roots of the characteristic Equation (7), obtained by numerical method, tend to the natural frequencies of elastic vibrations, fixed on the outer surface of the cylinder. In all of these cases, the solution of the spectral problem (7), in contrast to the composite semi-infinite rod, exists for any of the parameters of friction.

Figure 2 and Figure 3 show the dependence of the real (a) and imaginary (b) parts of the eigenvalues of the spectral problem (9), (18) the parameter and n = 0.4 respectively. The numbers marked on the charts number of oscillations in the ascending order of the real part of the Eigen values. In all cases, except for the first mode and the second mode (n = 4) for the real parts of these curves have the form of smooth decreasing steps with a maximum angle of inclination of the tangent to the segment corresponding imaginary parts have a characteristic maximum.

With the growing number of fashion maximum value increases, the value of a, to which he achieved increases, while remaining less than one. Meaning a, which peaks are shown in Table 1 and Table 2. In the zeros harmonic for any a there is zero eigenvalue and a smaller units exist purely imaginary eigenvalues, which tends to infinity when approaching the unit on the left. Zero eigenvalue corresponds to the motion of the cylinder as a ri- gid body. In the case of n = 1, 2 for the first mode, there are critical values respectively, starting from which complex eigenvalues becomes purely imaginary, i.e. oscillatory process is replaced by a perio- dic (Figure 4(a) and Figure 4(b)). At big data critical values of the imaginary part of the bifurcated,

(a)(b)

Figure 3. (a) The dependence of the real part of their own values of α (n = 4); (b) Dependence of the imaginary parts of the eigenvalues values of α (n = 4).

(a)(b)

Figure 4. (а) The dependence of the real part of their own values of α (n = 1, 2); (b) Dependence of the imaginary parts of the eigenvalues values of α.

Table 1. The values of the attenuation coefficient depending on the number of harmonics.

Table 2. The values of the maximum oscillation damping depending on the number of harmonics.

with one branch tend to zero tends to infinity, and the second increases indefinitely. (See Figure 4, the numbers marked on the charts numbered harmonics.)

For n = 3 also exists a critical value, branch from which the first and second modes are merged into one, and when minimum Eigen values of becomes red. Near the critical point at the imaginary part of the first two events there is a maximum in excess of the maximum of the other modes considered. In addition, the segment discovered purely imaginary roots, depending on which shown in Figure 5.

A similar case is obtained for n = 4. At the critical value branches of the second and third modes are merged, while second eigenvalues becomes a multiple. Near the critical point at the imaginary part of the second mode has a maximum exceeding the maximum of the rest of the considered modes. On the interval also found purely imaginary roots, whose dependence on.

Thus for all n there is considered imaginary branch of the natural frequencies of the parameter, which in the vicinity of the unit is broken continuity.

(a)(b)

Figure 4. (а) The dependence of the real part of their own values of α (n = 1, 2); (b) Dependence of the imaginary parts of the eigenvalues values of α.

Figure 5. The dependence of the imaginary part of its own values of α (n = 4).

5. Numerical Solution of the Problem on Its Own Plane Oscillations of a Cylinder

Solution of the resulting task was carried out by separation of variables and note to the solution of the transcendental equation. All results of the calculations are given in dimensionless system of units in which the value of the shear modulusm, density cylinder, radius of the cylinder Rconsidered to be equal to unity. Poisson’s ratio is assumed to be 0.25. In case иthe roots of the natural vibration frequencies of the free elastic cylinder. At, or, roots, obtained by numerical method tend to own oscillating elastic fixed to the outer surface of the cylinder. In all of these cases, the solution of the spectral problem, unlike composite semi-infinite rod, exists for any of the parameters of friction, as in the case ant planar cylinder oscillation.

Figure 6 and Figure 7 show the dependence of the real (a) and imaginary (b) parts of the eigen values of the spectral problem of the parameter . Figure 8 and Figure 9 ?n = 0 to 3, respectively. The numbers in the graphs denote the eigenvalues in ascending order of their real parts.

For n = 0 the problem is divided into two independent tasks. In this case, as in the case ant planar cylinder oscillation, depending on the real parts of the eigen values have the form of smooth decreasing steps with a maximum angle of inclination of the tangent in the case of radial oscillations in the interval (Figure 6(b)), torsions in the interval (Figure 8(a)). In these segments corresponding imaginary parts have a characteristic maximum at (Figure 6(b)), (Figure 8(b)).

As in the case anticline, with increasing numbers of harmonics increases the maximum value, except for the first radial root (see Table 3). It differs from the rest of the eigen values of the fact that the real part vanishes that corresponds to the motion of the cylinder as a rigid body.

For all the above cases, for n > 1, there is a clear separation of the roots into two types. The differences between these types of roots appear as a character of the dependence of the eigen values of the parameters of the external friction, and in the value of the form. For example, for the first root of the first harmonic-“twist”, the maximum value of the real part of the radial component of the voltage waveform is about three times smaller than the value of the real part component forms torsion stresses. For the second root of the first harmonic-“radial” ―the maximum value of the real part of the radial component of its own form of stress three times more than the maximum torsion component (see Figure 10(a), the first root; Figure 10(b), the second). Actual own forms part of the deformation, on the edge of the cylinder, characterized by two times (see Figure 11). The imaginary parts of their own forms of valid order of magnitude smaller and do not have such a pronounced difference. If you change depending on the real parts of the eigen values of the first type-“radial”―the parameter of friction have the form of smooth decreasing steps with a maximum angle of inclination of the tangent to the range except for the first mode of the second, third, fourth harmonics. Depending on the real parts of the eigenvalues of the second type―“torsion” have in this case the form is close to the line (see Figure 7(a)). In case of change. Depending on the real parts “tensional” eigenvalues have the form of decreasing levels of smoothed with a maximum angle of inclination of the tangent to the range, with the exception of the second mode of the second, third, fourth harmonics; a dependence of the real parts of the “radial” eigen val-

(a)(b)

Figure 6. (a) The dependence of the real part of the eigenvalues of α; (b) The dependence of the imaginary part of the eigenvalues of α.

(a)(b)

Figure 7. (a) The dependence of the real part of the eigenvalues of α; (b) The dependence of the imaginary part of the eigenvalues of α.

(a)(b)

Figure 8. (a) The dependence of the imaginary part of the eigenvalues of α; (b) The dependence of the imaginary part of the eigenvalues of α.

(a)(b)

Figure 9. (a) The dependence of the real part of the eigenvalues of α (n = 3); (b) The dependence of the imaginary part of the eigenvalues of α.

(a)(b)

Figure 10. (a) The dependence of the real part of the eigenvalues of α; (b) The dependence of the imaginary part of the eigenvalues of α.

Figure 11. The dependence of the real part of the eigenvalues of α.

Table 3. The values of the maximum oscillation damping depending on the mode number.

ues-lose to a linear form (see Figure 8(a) and Figure 9(a)). Actual part allocated in both cases the eigenvalues corresponding to the above defined ranges, reaches certain values and then decreases to zero. When changing imaginary part of the “radial” eigenvalues have a characteristic maximum in the interval, the value of which is ten times the value of the imaginary parts of the “tensional” eigenvalues on the whole interval under consideration (i.e., ,) (see Figure 7(b)). When changing behave similarly imaginary part of the “tensional” eigenvalues, reaching a maximum in the interval (see Figure 8(b) and Figure 9(b)). The imaginary parts of the selected eigenvalues at the vanishing real part of the bifurcated, one rushes to the root (see Figure 8(b) and Figure 9(b)). The imaginary parts of the selected eigen values at the vanishing real part of the bifurcated, one rushes to the root calculated as n increases and shifts to the right along the axis, split in two when (see Table 4). Unlike the case of Ante plane

Table 4. The values of the maximum oscillation damping depending on the number of harmonics.

vibrations of the cylinder there is no expression of the growth of the maximum values with increasing mode and shift it to the axis.

6. Conclusions

For all the cases considered flat fluctuations atn > 1, there is a clear separation of the roots into two types. The differences between these types of roots appear as a character of the dependence of the eigen values of the parameters of the external friction, and in the value of the form. For example, for the first root of the first harmonic-“twist”, the maximum value of the real part of the radial component of the voltage waveform is about three times smaller than the value of the real part component forms tensional stresses.

The imaginary parts of their own forms of valid order of magnitude smaller and do not have such a pronounced difference. When changing depending on the real parts of the eigenvalues of the first type―“radial”―the parameter of friction have the form of smooth decreasing steps with a maximum angle of inclination of the tangent to the range except for the first mode of the second, third, fourth harmonics. Depending on the real parts of the eigen values of the second type―“torsion” have in this case the form is close to linear.

For all cases considered anti plane oscillations n there imaginary branch of the natural frequencies of the parameter, which in the vicinity of the unit is broken continuity.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Rashidov, T.R. (1973) Dynamic Theory of Seismic Stability of Complex Systems of Underground Structures. Tashkent, 182 p.
[2]	Rashidov, T.R., Dorman, I.J. and Ishankhodjaev, A.A. (1975) Seismic Stability of Tunnel Construction of Subways. Moscow, 120 p.
[3]	Guz, A.N. and Golovchan, V.T. (1972) Diffraction of Elastic Waves in Multiply Bodies. Kiev, 254 p.
[4]	Kubenko, V.D. (1979) Unsteady Interaction of Structural Elements with the Environment. Kiev, 183 p.
[5]	Safarov, I.I. (1992) Oscillations and Waves in Dissipative Media and Nedorodnyhkonstruktsiyah. Tashkent, 250 with.
[6]	Bazarov, M.B., Safarov, I.I. and Shokin, Y.M. (1996) Numerical Modeling of Vibrations Dissipative Inhomogeneous and Homogeneous Mechanical Systems. Siberian Branch, Russian Academy of Sciences, Novosibirsk, 189 p.
[7]	Safarov, I.I., Chat, Z.I., Rakhmonov, K.K. and Umarov, A.O. (2013) Forced to Steady-State Oscillations of Cylindrical Bodies with an External Boundary Friction. 114-123.
[8]	Neumark, M.A. (1968) Linear Differential Operatory. Moscow, 528, p.
[9]	Safarov, I.I., Teshaev, M.Kh. and Boltaev, Z.I. (2012) Wave Processes in the Mechanical Waveguide. LAP LAMBERT Academic Publishing, Germany, 217 p.