Neutrosophic Soft Expert Sets

Mehmet Şahin¹, Shawkat Alkhazaleh², Vakkas Uluçay¹

¹Department of Mathematics, Gaziantep University, Gaziantep, Turkey.
²Department of Mathematics, Faculty of Science and Art, Shaqra University, Shaqra, KSA.

DOI: 10.4236/am.2015.61012                

Abstract

In this paper we introduce the concept of neutrosophic soft expert set (NSES). We also define its basic operations, namely complement, union, intersection, AND and OR, and study some of their properties. We give examples for these concepts. We give an application of this concept in a decision-making problem.

Keywords

Soft Expert Set, Neutrosophic Soft Set, Neutrosophic Soft Expert Set

1. Introduction

In some real-life problems in expert system, belief system, information fusion and so on, we must consider the truth-membership as well as the falsity-membership for proper description of an object in uncertain, ambiguous environment. Intuitionistic fuzzy sets were introduced by Atanassov [1] . After Atanassov’s work, Smarandache [2] [3] introduced the concept of neutrosophic set which is a mathematical tool for handling problems involving imprecise, indeterminacy and inconsistent data. In 1999, Molodtsov [4] initiated a novel concept of soft set theory as a new mathematical tool for dealing with uncertainties. After Molodtsov’s work, some different operations and applications of soft sets were studied by Chen et al. [5] and Maji et al. [6] . Later, Maji [7] firstly proposed neutrosophic soft sets with operations. Alkhazaleh et al. generalized the concept of fuzzy soft expert sets which include that possibility of each element in the universe is attached with the parameterization of fuzzy sets while defining a fuzzy soft expert set [8] . Alkhazaleh et al. [9] generalized the concept of parameterized interval- valued fuzzy soft sets, where the mapping in which the approximate function are defined from fuzzy parameters set, and they gave an application of this concept in decision making. In the other study, Alkhazaleh and Salleh [10] introduced the concept soft expert sets where user can know the opinion of all expert sets. Alkhazaleh and Salleh [11] generalized the concept of a soft expert set to fuzzy soft expert set, which is a more effective and useful. They also defined its basic operations, namely complement, union, intersection, AND and OR, and gave an application of this concept in decision-making problem. They also studied a mapping on fuzzy soft expert classes and its properties. Our objective is to introduce the concept of neutrosophic soft expert set. In Section 1, we introduce from intuitionistic fuzzy sets to soft expert sets. In Section 2, preliminaries are given. In Section 3, we also define the concept of neutrosophic soft expert set and its basic operations, namely complement, union, intersection AND and OR. In Section 4, we give an application of this concept in a decision-making problem. In Section 5 conclusions are given.

2. Preliminaries

In this section we recall some related definitions.

2.1. Definition: [3] Let U be a space of points (objects), with a generic element in U denoted by u. A neutrosophic set (N-sets) A in U is characterized by a truth-membership function T_A, a indeterminacy-membership function I_A and a falsity-membership function F_A.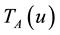; and 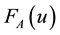are real standard or nonstandard subsets of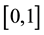. It can be written as

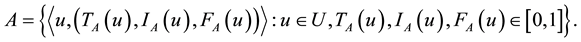
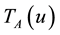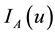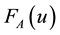There is no restriction on the sum of; and, so

.

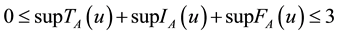2.2. Definition: [7] Let U be an initial universe set and E be a set of parameters. Consider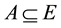. Let denotes the set of all neutrosophic sets of U. The collection 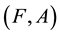is termed to be the soft neutrosophic set over U, where F is a mapping given by.

2.3. Definition: [6] A neutrosophic set A is contained in another neutrosophic set B i.e. 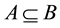if, , ,.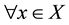

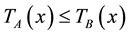Let U be a universe, E a set of parameters, and X a soft experts (agents). Let O be a set of opinion, and.

2.4. Definition: [9] A pair (F, A) is called a soft expert set over U, where F is mapping given by where denotes the power set of U.

2.5. Definition: [11] A pair is called a fuzzy soft expert set over U, where F is mapping given by where denotes the set of all fuzzy subsets of U.

2.6. Definition: [11] For two fuzzy soft expert sets and over U, is called a fuzzy soft expert subset of if

1)

2), is fuzzy subset of

This relationship is denoted by. In this case is called a fuzzy soft expert superset of.

2.7. Definition: [11] Two fuzzy soft expert sets and over U are said to be equal.

If is a fuzzy soft expert subset of and is a fuzzy soft expert subset of.

2.8. Definition: [11] An agree-fuzzy soft expert set over U is a fuzzy soft expert subset of defined as follow

.

2.9. Definition: [11] A disagree-fuzzy soft expert set over U is a fuzzy soft expert subset of defined as follow

.

2.10. Definition: [11] Complement of a fuzzy soft expert set. The complement of a fuzzy soft expert set denoted by and is defined as where is mapping given by

where is a fuzzy complement.

2.11. Definition: [11] The intersection of fuzzy soft expert sets and over U, denoted by, is the fuzzy soft expert set where and,

where t is a t-norm.

2.12. Definition: [11] The intersection of fuzzy soft expert sets and over U, denoted by, is the fuzzy soft expert set where and,

where s is an s-norm.

2.13. Definition: [11] If and are two fuzzy soft expert sets over U then “AND” denoted by is defined by

such that, where t is a t-norm.

2.14. Definition: [11] If and are two fuzzy soft expert sets over U then “OR” denoted by is defined by

such that, where s is an s-norm.

Using the concept of neutrosophic set now we introduce the concept of neutrosophic soft expert set.

3. Neutrosophic Soft Expert Set

In this section, we introduce the definition of a neutrosophic soft expert set and give basic properties of this concept.

Let U be a universe, E a set of parameters, X a set of experts (agents), and a set of opinions. Let and.

3.1. Definition: A pair is called a neutrosophic soft expert set over U, where F is mapping given by

where denotes the power neutrosophic set of U. For definition we consider an example.

3.1. Example: Suppose the following U is the set of car under consideration E is the set of parameters. Each parameter is a neutrosophic word or sentence involving neutrosophic words.

be a set of experts. Suppose that

The neutrosophic soft expert set is a parameterized family of all neutrosophic sets of U and describes a collection of approximation of an object.

3.1. Definition: Let and be two neutrosophic soft expert sets over the common universe U. is said to be neutrosophic soft expert subset of, if and, , , We denote it by.

is said to be neutrosophic soft expert superset of if is a neutrosophic soft expert subset of. We denote by.

3.2. Example: Suppose that a company produced new types of its products and wishes to take the opinion of some experts about concerning these products. Let be a set of product, a set of decision parameters where denotes the decision “easy to use”, “quality” respectively and let be a set of experts. Suppose

Clearly. Let and be defined as follows:

Therefore

.

3.3. Definition: Equality of two neutrosophic soft expert sets. Two (NSES), and over the common universe U are said to be equal if is neutrosophic soft expert subset of and is neutrosophic soft expert subset of.We denote it by

.

3.4. Definition: NOT set of set parameters. Let be a set of parameters. The NOT set of E is denoted by where not,.

3.3. Example: Consider 3.2.example. Here

3.5. Definition: Complement of a neutrosophic soft expert set. The complement of a neutrosophic soft expert set denoted by and is defined as where is map-

ping given by neutrosophic soft expert complement with, ,.

3.4. Example: Consider the 3.1 Example. Then describes the “not easy to use of the car” we have

3.6. Definition: Empty or null neutrosophic soft expert set with respect to parameter. A neutrosophic soft expert set over the universe U is termed to be empty or null neutrosophic soft expert set with respect to the parameter A if

.

In this case the null neutrosophic soft expert set (NNSES) is denoted by.

3.5. Example: Let the set of three cars be considered as universal set be the set of parameters that characterizes the car and let be a set of experts.

Here the (NNSES) is the null neutrosophic soft expert sets.

3.7. Definition: An agree-neutrosophic soft expert set over U is a neutrosophic soft expert subset of defined as follow

.

3.6. Example: Consider 3.1. Example. Then the agree-neutrosophic soft expert set over U is

3.8. Definition: A disagree-neutrosophic soft expert set over U is a neutrosophic soft expert subset of defined as follow

.

3.7. Example: Consider 3.1. Example. Then the disagree-neutrosophic soft expert set over U is

3.9. Definition: Union of two neutrosophic soft expert sets.

Let and be two NSESs over the common universe U. Then the union of and is denoted by “” and is defined by, where and the truth- membership, indeterminacy-membership and falsity-membership of are as follows:

3.8. Example: Let and be two NSESs over the common universe U

Therefore

3.10. Definition: Intersection of two neutrosophic soft expert sets. Let and be two NSESs over the common universe U. Then the intersection of and is denoted by “” and is defined by, where and the truth-membership, indeterminacy-membership and falsity-membership of are as follows:

3.9. Example: Let and be two NSESs over the common universe U

Therefore

.

3.1. Proposition: If and are neutrosophic soft expert sets over U. Then

1)

2)

3)

4)

5)

Proof: 1) We want to prove that by using 3.9 definition and we consider the case when if as the other cases are trivial, then we have

The proof of the propositions 2) to 5) are obvious.

3.2. Proposition: If, and are three neutrosophic soft expert sets over U. Then

1)

2)

Proof: 1) We want to prove that by using 3.9 definition and we consider the case when if as the other cases are trivial, then we have

We also consider her the case when as the other cases are trivial, then we have

2) The proof is straightforward.

3.3. Proposition: If, and are three neutrosophic soft expert sets over U. Then

1)

2)

Proof: We use the same method as in the previous proof.

3.11. Definition: AND operation on two neutrosophic soft expert sets. Let and be two NSESs over the common universe U. Then “AND” operation on them is denoted by “” and is defined by where the truth-membership, indeterminacy-membership and falsity-member- ship of are as follows:

3.10. Example: Let and be two NSESs over the common universe U. Then and is a follows:

Therefore

3.12. Definition: OR operation on two neutrosophic soft expert sets. Let and be two NSESs over the common universe U. Then “OR” operation on them is denoted by “” and is defined by where the truth-membership, indeterminacy-membership and falsity-membership of are as follows:

3.11. Example: Let and be two NSESs over the common universe U. Then OR is a follows:

Therefore

3.4. Proposition: If and are neutrosophic soft expert sets over U. Then

1)

2)

Proof: 1) Let and

be two NSESs over the common universe. Also let, where

Therefore

Again

Hence the result is proved.

3.5. Proposition: If, and are three neutrosophic soft expert sets over U. Then

1)

2)

3)

4)

Proof: We use the same method as in the previous proof.

4. An Application of Neutrosophic Soft Expert Set

In this section, we present an application of neutrosophic soft expert set theory in a decision-making problem. The problem we consider is as below:

Suppose that a hospital to buy abed. Seven alternatives are as follows:

,

suppose there are five parameters where the parameters stand for “medical bed”, “soft bed”, “orthopedic bed”, “moving bed”, “air bed”, respectively. Let be a set of experts. Suppose:

In Table 1 and Table 2 we present the agree-neutrosophic soft expert set and disagree-neutrosophic soft expert set, respectively, such that if then otherwise, and if then otherwise where are the entries in Table 1 and Table 2.

The following algorithm may be followed by the hospital wants to buy a bed.

1) input the neutrosophic soft expert set,

2) find an agree-neutrosophic soft expert set and a disagree-soft expert set,

3) find for agree-neutrosophic soft expert set,

4) find for disagree-neutrosophic soft expert set,

5) find

6) find m, for which

Table 1. Agree-neutrosophic soft expert set.

Table 2. Disagree-neutrosophic soft expert set.

Table 3..

Then is the optimal choice object. If m has more than one value, then any one of them could be chosen by hospital using its option. Now we use this algorithm to find the best choices for to get to the hospital bed. From Table 1 and Table 2 we have Table 3.

Then, so the hospital will select the bed. In any case if they do not want to choose due to some reasons they second choice will be.

5. Conclusion

In this paper, we have introduced the concept of neutrosophic soft expert set which is more effective and useful and studied some of its properties. Also the basic operations on neutrosophic soft expert set namely complement, union, intersection, AND and OR have been defined. Finally, we have presented an application of NSES in a decision-making problem.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Atanassov, K. (1986) Intuitionistic Fuzzy Sets. Fuzzy Sets and Systems, 20, 87-96. http://dx.doi.org/10.1016/S0165-0114(86)80034-3
[2]	Smarandache, F. (2005) Neutrosophic Set, a Generalization of the Intuitionistic Fuzzy Sets. International Journal of Pure and Applied Mathematics, 24, 287-297.
[3]	Smarandache, F. (1998) A Unifying Field in Logics. Neutrosophy: Neutrosophic Probability, Set and Logic. American Research Press, Rehoboth.
[4]	Molodtsov, D.A. (1999) Soft Set Theory-First Results. Computers and Mathematics with Applications, 37, 19-31. http://dx.doi.org/10.1016/S0898-1221(99)00056-5
[5]	Chen, D., Tsang, E.C.C., Yeung, D.S. and Wang, X. (2005) The Parameterization Reduction of Soft Sets and Its Application. Computers and Mathematics with Applications, 49, 757-763. http://dx.doi.org/10.1016/j.camwa.2004.10.036
[6]	Maji, P.K., Roy, A.R. and Biswas, R. (2003) Soft Set Theory. Computers and Mathematics with Applications, 45, 555-562. http://dx.doi.org/10.1016/S0898-1221(03)00016-6
[7]	Maji, P.K. (2013) Neutrosophic Soft Set. Computers and Mathematics with Applications, 45, 555-562. http://dx.doi.org/10.1016/S0898-1221(03)00016-6
[8]	Alkhazaleh, S., Salleh, A.R. and Hassan, N. (2011) Possibility Fuzzy Soft Set. Advances in Decision Sciences, 2011, Article ID: 479756. http://dx.doi.org/10.1155/2011/479756
[9]	Alkhazaleh, S., Salleh, A.R. and Hassan, N. (2011) Fuzzy Parameterized Interval-Valued Fuzzy Soft Set. Applied Mathematical Sciences, 5, 3335-3346.
[10]	Alkhazaleh, S. and Salleh, A.R. (2011) Soft Expert Sets. Advances in Decision Sciences, 2011, Article ID: 757868. http://dx.doi.org/10.1155/2011/757868
[11]	Alkhazaleh, S. and Salleh, A.R. (2014) Fuzzy Soft Expert Set and Its Application. Applied Mathematics, 5, 1349-1368. http://dx.doi.org/10.4236/am.2014.59127