Nonlinear General Integral Control Design via Equal Ratio Gain Technique

Baishun Liu^*

Academy of Naval Submarine, Qingdao, China.

DOI: 10.4236/ijmnta.2014.35028                

Abstract

This paper proposes two kinds of nonlinear general integral controllers, that is, one is generic and another is practical, for a class of uncertain nonlinear system. By extending equal ratio gain technique to a canonical interval system matrix and using Lyapunov method, theorems to ensure regionally as well as semi-globally asymptotic stability are established in terms of some bounded information. Moreover, for the practical nonlinear integral controller, a real time method to evaluate the equal ratio coefficient is proposed such that its value can be chosen moderately. Theoretical analysis and simulation results demonstrated that not only nonlinear general integral control can effectively deal with the uncertain nonlinear system but also equal ratio gain technique is a powerful and practical tool to solve the control design problem of dynamics with the nonlinear and uncertain actions.

Keywords

General Integral Control, Nonlinear Control, Robust Control, Generic Controller, Equal Ratio Gain Technique, Output Regulation

1. Introduction

Integral control [1] plays an important role in practice because it ensures asymptotic tracking and disturbance rejection when exogenous signals are constants or planting parametric uncertainties appears. However, nonlinear general integral control design is not trivial matter because it depends on not only the uncertain nonlinear actions and disturbances but also the nonlinear control actions. Therefore, it is of important significance to develop the design method for nonlinear general integral control.

For general integral control design, there were various design methods, such as general integral control design based on linear system theory, sliding mode technique, feedback linearization technique and singular perturbation technique and so on, were presented by [2] -[5] , respectively. In addition, general concave integral control [6] , general convex integral control [7] , constructive general bounded integral control [8] and the generalization of the integrator and integral control action [9] were all developed by using Lyapunov method and resorting to a known stable control law. Equal ratio gain technique firstly was proposed by [10] , and was used to address the linear general integral control design for a class of uncertain nonlinear system.

All these general integral controllers above constitute only a minute portion of general integral control, and therefore lack generalization. Moreover, in consideration of the complexity of nonlinear system, it is clear that we can not expect that a particular integral controller has the high control performance for all nonlinear system. Thus, the generalization of general integral controller naturally appears since for all nonlinear system, we can not enumerate all the categories of integral controllers with high control performance. It is not hard to know that this is a very valuable and challenging problem, and equal ratio gain technique can be used to deal with this trouble since it is a powerful and practical tool to solve the nonlinear control design problem.

Motivated by the cognition above, this paper proposes a generic nonlinear integral controller and a practical nonlinear integral controller for a class of uncertain nonlinear system. The main contributions are that: 1) By defining two function sets, the generalization of general integral controller is achieved; 2) A canonical interval system matrix can be designed to be Hurwitz as any row controller gains, or controller and its integrator gains increase with the same ratio; 3) Theorems to ensure regionally as well as semi-globally asymptotic stability is established in terms of some bounded information. Moreover, for the practical nonlinear integral controller, a real time method to evaluate the equal ratio coefficient is proposed such that its value can be chosen moderately. Theoretical analysis and simulation results demonstrated that not only nonlinear general integral control can effectively deal with the uncertain nonlinear system but also equal ratio gain technique is a powerful and practical tool to solve the control design problem of dynamics with the nonlinear and uncertain actions.

Throughout this paper, we use the notation 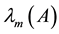and 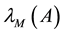to indicate the smallest and largest eigenva- lues, respectively, of a symmetric positive define bounded matrix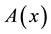, for any. The norm of vector x is

defined as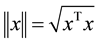, and that of matrix A is defined as the corresponding induced norm.

The remainder of the paper is organized as follows: Section 2 describes the system under consideration, assumption and definition. Sections 3 and 4 present the generic and practical nonlinear integral controllers along with their design method, respectively. Example and simulation are provided in Section 5. Conclusions are presented in Section 6.

2. Problem Formulation

Consider the following controllable nonlinear system,

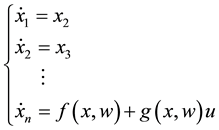(1)

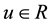where is the state; is the control input; is a vector of unknown constant parameters and disturbances. The function 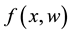is the uncertain nonlinear action, and the uncertain nonlinear function is continuous in on the control domain. We want to design a control law 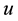such that 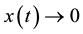as.

Assumption 1: There is a unique pair that satisfies the equation,

(2)

so that is the desired equilibrium point and is the steady-state control that is needed to maintain equilibrium at.

Assumption 2: Suppose that the functions and satisfy the following inequalities,

(3)

(4)

(5)

(6)

for all and. where, , , and are all positive constants.

Definition 1: with, and denotes the set of all continuous functions, such that

and

hold for all and. Where is a point on the line segment connecting to.

Definition 2: with, and denotes the set of all integrable functions, such that

and

hold for all. Where is a point on the line segment connecting to the origin.

3. Generic Nonlinear Integral Control

The generic nonlinear integral controller is given as,

(7)

where and belong to the function sets and, respectively, , and are all positive constants.

Thus, substituting (7) into (1), obtain the augmented system,

(8)

By Assumption 1 and choosing to be large enough, and then setting and of the system (8), obtain,

(9)

Therefore, we ensure that there is a unique solution, and then is a unique equilibrium point of the closed-loop system (8) in the domain of interest. At the equilibrium point, , irrespective of the value of.

Now, by Definition 1, 2 and, and can be written as,

(10)

(11)

where and.

Thus, substituting (9)-(11) into (8), obtain,

(12)

where

And is an matrix, all its elements are equal to zero except for

Moreover, it is worthy to note that the function is integrated into via a change of variable. This has not influence on the results if the inequality (4) holds and it can be taken as in the design. Therefore, it is omitted in all the following demonstrations.

For analyzing the stability of closed-loop system (12), we must ensure that the matrix is Hurwitz for all, , and. This can be achieved by Routh’s stability criterion.

3.1. Hurwitz Stability

Hurwitz stability of the matrix can be achieved by Routh’s stability criterion, which is motivated by the idea [10] , as follows:

Step 1: the polynomial of the matrix with is,

(13)

By Routh’s stability criterion, and can be chosen such that the polynomial (13) is Hurwitz for all and. Obviously, if and are all large to zero, and then the necessary condition, that is, the coefficients of the polynomial (13) are all positive, is naturally satisfied.

Step 2: based on the gains, and Hurwitz stability condition to be obtained by Step 1, the maximums of and, that is, and, can be obtained, respectively. Since and interact, there exist innumerable and. Thus, two kinds of typical cases are interesting, that is, one is that is evaluated with; another is that let, and then can be obtained together.

Step 3: by and obtained by Step 2, check Hurwitz stability of the matrix for all and. If it does not hold, redesign and and repeat the previous steps until the matrix is Hurwitz for all and.

It is well known that Hurwitz stability condition is more and more complex as the order of the matrix increases. Thus, for clearly illustrating the design method above, we consider two kinds of cases, that is, and, respectively, as follows:

Case 1: for, the polynomial (13) is,

(14)

By Routh’s stability criterion, if, , , , and are all positive numbers, and the following inequality,

(15)

holds, and then the polynomial (14) is Hurwitz for all and.

Sub-class 1:, and are multiplied by, and then substituting them into (15), obtain,

(16)

By the inequality (16), obtain,

Sub-class 2:, , , and are multiplied by, and then substituting them into (15), obtain,

(17)

For this sub-class, there are two kinds of cases:

1) if, and then by the inequality (17), obtain,

2) if, and then by the inequality (17), obtain,

Case 2: for, the polynomial (13) is,

(18)

By Routh’s stability criterion, if, , , , , and are all positive numbers, and the following inequality,

(19)

holds, and then the polynomial (18) is Hurwitz for all and.

Sub-class 1:, , and are multiplied by, and then substituting them into (19), obtain,

(20)

By the inequality (20), obtain,

Sub-class 2:, , , , , and are multiplied by, and then substituting them into (19), obtain,

For this sub-class, although the situation is complex, a moderate solution can still be obtained, that is,

From the demonstration above, it is obvious that for, and or of the matrix, there all exist such that the matrix is Hurwitz for all, and. Therefore, for the high order matrix, the same result can be still obtained with the help of computer. Thus, we can conclude that the n+1-order matrix can be designed to be Hurwitz for all, , and.

Theorem 1: There exist and such that the system matrix for is Hurwitz, and then it is still Hurwitz for all and.

Discussion 1: From the statements above, it is easy to see that: 1) the system matrix is an interval matrix; 2) in consideration of the controllable canonical form of linear system, the system matrix can be called as the controllable canonical interval system matrix; 3) although Theorem 1 is demonstrated by the single variable system matrix, it is easy to extend Theorem 1 to the multiple variable case since Routh’s stability criterion applies to not only the single variable system matrix but also the multiple variable one. Thus, the following proposition can be established.

Proposition 1: A canonical interval system matrix can be designed to be Hurwitz as any row controller gains, or controller and its integrator gains increase with the same ratio.

3.2. Closed-Loop Stability Analysis

The matrix can be designed to be Hurwitz for all, , and. Thus, by linear system theory, if the matrix is Hurwitz, and then for any given positive define symmetric matrix, there exists positive define symmetric matrix that satisfies Lyapunov equation. Therefore, the solution of Lyapunov equation [11] is,

(21)

where

, and

Thus, using as Lyapunov function candidate, and then its time derivative along the trajectories of the closed-loop systems (12) is,

(22)

where.

Now, using the inequalities (3), (5) and (6), obtain,

(23)

where is a positive constant.

Substituting (23) into (22), and using, obtain,

(24)

By proposition proposed by [10] , that is, as any row controller gains, or controller and its integrator gains of a canonical system matrix tend to infinity with the same ratio, if it is always Hurwitz, and then the same row solutions of Lyapunov equation all tend to zero, we have,

1) as

2) as

where.

Although there is innumerable, the maximum exists and as. Thus, there exist with, or such that the following inequality,

(25)

holds for all with, or. Therefore, we have.

Using the fact that Lyapunov function is a positive define function and its time derivative is a negative define function if the inequality (25) holds, we conclude that the closed-loop system (12) is stable. In fact, means and. By invoking LaSalle’s invariance principle, it is easy to know that the closed-loop system (12) is exponentially stable. As a result, the following theorem can be established.

Theorem 2: Under Assumptions 1 and 2, if the system matrix is Hurwitz for all

, ,

and

and then the equilibrium points and of the closed-loop system (12) is an exponentially stable for all

with, or

Moreover, if all assumptions hold globally, then it is globally exponentially stable.

Remark 1: From the statements of Subsections 3.1 and 3.2, it is to see that: by extending equal ratio gain technique to a canonical interval system matrix and using Lyapunov method, the asymptotic stability of the uncertain nonlinear system with generic nonlinear integral control can be ensured in terms of some bounded information. This shows that not only nonlinear general integral control can effectively deal with the uncertain nonlinear system but also equal ratio gain technique is a powerful tool to solve the control design problem of dynamics with the nonlinear and uncertain actions.

Discussion 2: From the statements above, it is obvious that: although the generalization of nonlinear general integral control is achieved by defining two function sets, there are two unavoidable drawbacks, that is, one is that the controller (7) is too generic such that it is shortage of pertinence; another is that it is difficulty to obtain the less conservative or such that it is shortage of practicability. All these mean that Theorem 2 has only theoretical significance and not practical significance. Therefore, a practical nonlinear integral controller along with a new design method is proposed to solve these troubles in the next Section.

4. Practical Nonlinear Integral Control

For making up the shortage indicated by Discussion 2, a practical nonlinear integral controller is given as,

(26)

where, ,

and are the slopes of the line segment connecting to the origin, and they are utilized to harmonize the actions of in the controller and integrator, respectively. is used to attenuate the uncertain nonlinear action of. is applied to improve

the performance of integral control action. is used to reorganize the integrator

output., and are all positive constants, and.

Assumptions 3: By the definition of the controller (26), it is convenient to suppose that the following inequalities,

(27)

(28)

hold for all, and, where and are all positive constants.

By the same way as Section 3, we have,

(29)

where,

is an matrix, all its elements are equal to zero except for

and the functions and are integrated into and, respectively.

By the design method proposed by Subsection 3.1, the system matrix can be designed to be Hurwitz for all, , , and . Thus, by linear system theory, there exists positive define symmetric matrix that satisfies Lyapunov equation for any given positive define symmetric matrix. Therefore, we can utilize as Lyapunov function candidate, and then its time derivative along the trajectories of the closed-loop system (29) is,

(30)

where.

Now, using the inequalities (4), (5), (6), (27) and (28), obtain,

(31)

where is a positive constant.

Substituting (31) into (30), obtain,

(32)

By proposition proposed by [10] (details see Subsection 3.2), for any moment, there exists with, or such that the inequality,

(33)

holds for all with, or. Consequently, if

the inequality (33) holds for all, and then we conclude that holds uniformly in.

Using the fact that Lyapunov function is a positive define function and its time derivative is a negative define function if the inequality (33) holds for all, we conclude that the closed-loop system (29)

is stable. In fact, means and. By invoking LaSalle’s invariance principle, it is easy

to know that the closed-loop system (29) is uniformly exponentially stable. As a result, we have the following theorem.

Theorem 3: Under Assumptions 1, 2 and 3, if the system matrix is Hurwitz for all

, , , and

and then the equilibrium point and of the closed-loop system (29) is uniformly exponentially stable for all

with, or

Moreover, if all assumptions hold globally, and then it is globally uniformly exponentially stable.

Now, the design task is to provide a method to evaluate the instantaneous value with, or. To achieve this objective, the procedure can be summarized as follows:

Firstly, by the definitions of and, the instantaneous values and can be given as,

and

Secondly, by the inequality (33), the impermissible minimum of is,

Finally, by the limitation conditions,

with, or

and the iterative method to solve Lyapunov equation,

with, or can be obtained.

Discussion 3: From the statements above, it is easy to see that: 1) all the component of the nonlinear integral controller (26) have the clear actions; 2) is not greater than since can be used to attenuate the

uncertain nonlinear action of and can be designed moderately; 3)

or is less conservative since they are all evaluated by the instantaneous values and. All these not only solve the problem indicated by Discussion 2 but also mean that equal ratio gain technique is a powerful and practical tool to solve the control design problem of dynamics with the nonlinear and uncertain actions.

5. Example and Simulation

Consider the pendulum system [1] described by,

where, is the angle subtended by the rod and the vertical axis, and is the torque applied to the pendulum. View as the control input and suppose we want to regulate to. Now, taking, , the pendulum system can be written as,

and then it can be verified that is the steady-state control that is needed to maintain equilibrium at the origin.

By the practical nonlinear integral controller (26), the control law can be given as,

Thus, it is easy to obtain, , , and, and then the closed-loop system can be written as,

where,

and

The normal parameters are and, and in the perturbed case, and are reduced to 1

and 5, respectively, corresponding to double the mass. Thus, we have.

Now, with, , , , , and, the following inequality,

holds for all, and then the matrix is Hurwitz for all. Consequently, taking as the initial value, the simulation is implemented under the normal and perturbed cases, respectively. Moreover, in the perturbed case, we consider an additive impulse-like disturbance of magnitude 60 acting on the system input between 15 s and 16 s.

Figure 1 and Figure 2 showed the simulation results under normal (solid line) and perturbed (dashed line) cases. The following observations can be made: 1) The instantaneous value holds for all, , , , , , and. This shows that the closed-loop system is uniformly asymptotic stable and the equal ratio coefficient can be used to improve the conservatism. 2) The system responses are almost identical before the additive impulse-like disturbance appears. This means that by equal ratio gain technique, we can tune a nonlinear general integral controller with good robustness and high control performance. All these demonstrate that not only nonlinear general integral control can effectively deal with the uncertain nonlinear system but also equal ratio gain technique is a powerful and practical tool to solve the control design problem of dynamics with the nonlinear and uncertain actions.

Figure 1. The values of under normal (solid line) and perturbed case (dashed line).

Figure 2. System output under normal (solid line) and perturbed case (dashed line).

6. Conclusions

This paper proposes a generic nonlinear integral controller and a practical nonlinear integral controller for a class of uncertain nonlinear system. The main contributions are that: 1) By defining two function sets, the generalization of general integral controller is achieved; 2) A canonical interval system matrix can be designed to be Hurwitz as any row controller gains, or controller and its integrator gains increase with the same ratio; 3) Theorems to ensure regionally as well as semi-globally asymptotic stability are established in terms of some bounded information. Moreover, for the practical nonlinear integral controller, a real time method to evaluate the equal ratio coefficient is proposed such that its value can be chosen moderately.

Theoretical analysis and simulation results demonstrated that not only nonlinear general integral control can effectively deal with the uncertain nonlinear system but also equal ratio gain technique is a powerful and practical tool to solve the control design problem of dynamics with the nonlinear and uncertain actions.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Khalil, H.K. (2007) Nonlinear Systems. 3rd Edition, Electronics Industry Publishing, Beijing, 449-453, 551.
[2]	Liu, B.S. and Tian, B.L. (2012) General Integral Control Design Based on Linear System Theory. Proceedings of the 3rd International Conference on Mechanic Automation and Control Engineering, 5, 3174-3177.
[3]	Liu, B.S. and Tian, B.L. (2012) General Integral Control Design Based on Sliding Mode Technique. Proceedings of the 3rd International Conference on Mechanic Automation and Control Engineering, 5, 3178-3181.
[4]	Liu, B.S., Li, J.H. and Luo, X.Q. (2014) General Integral Control Design via Feedback Linearization. Intelligent Control and Automation, 5, 19-23. http://dx.doi.org/10.4236/ica.2014.51003
[5]	Liu, B.S., Luo, X.Q. and Li, J.H. (2014) General Integral Control Design via Singular Perturbation Technique. International Journal of Modern Nonlinear Theory and Application, 3, 173-181. http://dx.doi.org/10.4236/ijmnta.2014.34019
[6]	Liu, B.S., Luo, X.Q. and Li, J.H. (2013) General Concave Integral Control. Intelligent Control and Automation, 4, 356-361. http://dx.doi.org/10.4236/ica.2013.44042
[7]	Liu, B.S., Luo, X.Q. and Li, J.H. (2014) General Convex Integral Control. International Journal of Automation and Computing, 11, 565-570. http://dx.doi.org/10.1007/s11633-014-0813-6
[8]	Liu, B.S. (2014) Constructive General Bounded Integral Control. Intelligent Control and Automation, 5, 146-155. http://dx.doi.org/10.4236/ica.2014.53017
[9]	Liu, B.S. (2014) On the Generalization of Integrator and Integral Control Action. International Journal of Modern Nonlinear Theory and Application, 3, 44-52. http://dx.doi.org/10.4236/ijmnta.2014.32007
[10]	Liu, B.S. (2014) Equal Ratio Gain Technique and Its Application in Linear General Integral Control. International Journal of Modern Nonlinear Theory and Application.
[11]	Gajic, Z. (1995) Lyapunov Matrix Equation in System Stability and Control. Mathematics in Science and Engineering, 195, 30-31.