Low-Rank Positive Approximants of Symmetric Matrices

Achiya Dax

Hydrological Service, Jerusalem, Israel.

DOI: 10.4236/alamt.2014.43015                

Abstract

Given a symmetric matrix X, we consider the problem of finding a low-rank positive approximant of X. That is, a symmetric positive semidefinite matrix, S, whose rank is smaller than a given positive integer, , which is nearest to X in a certain matrix norm. The problem is first solved with regard to four common norms: The Frobenius norm, the Schatten p-norm, the trace norm, and the spectral norm. Then the solution is extended to any unitarily invariant matrix norm. The proof is based on a subtle combination of Ky Fan dominance theorem, a modified pinching principle, and Mirsky minimum-norm theorem.

Keywords

Low-Rank Positive Approximants, Unitarily Invariant Matrix Norms

1. Introduction

Let 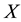be a given real symmetric 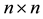matrix. In this paper we consider the problem of finding a low-rank symmetric positive semidefinite matrix which is nearest to 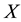with regard to a certain matrix norm. Let be a given unitarily invariant matrix norm on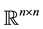. (The basic features of such norms are explained in the next section.) Let 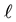be a given positive integer such that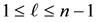, and define

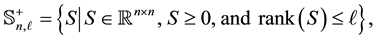
where the notation 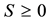means that 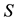is symmetric and positive semidefinite. Then the problem to solve has the form

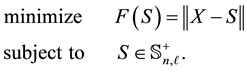(1.1)

The need for solving such problems arises in certain matrix completion methods that consider Euclidean distance matrices, see [1] or [2] . Since 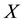is assumed to be a symmetric matrix, it has a spectral decom- position

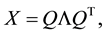(1.2)

where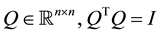, is an orthonormal matrix

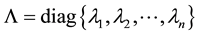
is a diagonal matrix, and

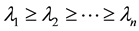
are the eigenvalues of in decreasing order. If, then and the spectral decomposition (1.2) coincides with the SVD of. In this case the solution of (1.1) is given by the Eckart-Young-Mirsky theorem. See the next section.

The rest of the paper assumes, therefore, that. In this case the solution of (1.1) is related to that of the problem

(1.3)

where

Let be a non-negative integer that counts the number of positive eigenvalues. That is

(1.4)

Let the diagonal matrix denotes the positive part of,

(1.5)

(If then, and is the null matrix.) Then, as we shall see in Section 3, the matrix

solves (1.3) in any unitarily invariant norm.

If then, clearly, is also a solution of (1.1). Hence in the rest of the paper we assume that. This assumption implies that the diagonal matrix

(1.6)

belongs to. The aim of the paper is to show that the matrix

solves (1.1) for any unitarily invariant norm.

Let be a given real matrix. Then another related problem is

(1.7)

The relation between (1.7) and (1.3) is seen when using the Frobenius matrix norm. Let be a symmetric matrix and let be a skew-symmetric matrix. Then, clearly,

(1.8)

Recall also that any matrix has a unique presentation as the sum where is symmetric and is skew-symmetric. Consequently, for any symmetric matrix, say,

(1.9)

Therefore, when using the Frobenius norm, a solution of (1.3) provides a solution of (1.7). This observation is due to Higham [3] . A matrix that solves (1.7) or (1.3) is called “positive approximant”. Similarly, the term “low-rank positive approximant” refers to a matrix that solves (1.1).

The current interest in positive approximants was initiated in Halmos’ paper [4] , which considers the solution of (1.7) in the spectral norm. Rogers and Ward [5] considered the solution of (1.7) in the Schatten-p norm, Ando [6] considered this problem in the trace norm, and Higham [3] considered the Frobenius norm. Halmos [4] has considered the positive approximant problem in a more general context of linear operators on a Hilbert space. Other positive approximants problems (in the operators context) are considered in [7] - [11] . The problems (1.1), (1.3) and (1.7) fall into the category of “matrix nearness problems”. Further examples of matrix (or operator) nearness problems are discussed in [12] - [18] . A review of this topic is given in Higham [19] .

The plan of the paper is as follows. In the next section we introduce notations and tools which are needed for the coming discussions. In Section 3 we show that solves (1.3). Section 4 considers the solution of (1.1) in Frobenius norm. This involves the Eckart-Young theorem. In the next sections Mirsky theorem extends the results to Schatten-p norms, the trace norm, and the spectral norm. Then it is proved that solves (1.1) in any unitarily invariant norm. The proof of this claim requires a subtle combination of Ky Fan dominance theorem, a modified pinching principle, and Mirsky theorem.

2. Notations and Tools

In this section we introduce notations and facts which are needed for coming discussions. Here denotes a real matrix with. Let

(2.1)

be an SVD of, where is an orthogonal matrix, is an orthogonal matrix, and is an diagonal matrix. The singular values of are assumed to be nonnegative and sorted to satisfy

(2.2)

The columns of and are called left singular vectors and right singular vectors, respectively. These vectors are related by the equalities

(2.3)

A further consequence of (2.1) is the equality

(2.4)

Moreover, let denotes the rank of. Then, clearly,

(2.5)

So (2.4) can be rewritten as

(2.6)

Let the matrices

(2.7)

be constructed from the first columns of and, respectively. Let be a diagonal matrix. Then the matrix

(2.8)

is called a rank-k truncated SVD of. (If then this matrix is not unique.)

Let denote the entries of the matrices, respectively. Then (2.4) indicates that

(2.9)

and

(2.10)

where the last inequality follows from the Cauchy-Schwarz inequality and the fact that the columns of and have unit length.

Another useful property regards the concepts of majorization and unitarily invariant norms. Recall that a matrix norm on is called unitarily invariant if the equalities

(2.11)

are satisfied for any matrix, and any pair of unitary matrices and. Let and be a given pair of matrices with singular values

respectively. Let and denote the corresponding n-vectors of singular values. Then the weak majorization relation means that these vectors satisfy the inequality

(2.12)

In this case we say that is weakly majorized by, or that the singular values of are weakly majorized by those of. The dominance theorem of Fan [20] [21] relates these two concepts. It says that if the singular values of are weakly majorized by those of then the inequality

(2.13)

holds for any unitarily invariant norm. For detailed proof of this fact see, for example, [8] , [20] - [23] . The most popular example of an unitarily invariant norm is, perhaps, the Frobenius matrix norm

(2.14)

which satisfies

(2.15)

Other examples are the Schatten p-norms,

(2.16)

and Ky Fan k-norms,

(2.17)

The trace norm,

(2.18)

is obtained for and, while the spectral norm

(2.19)

corresponds to and. The use of Ky Fan k-norms enables us to state the dominance principle in the following way.

Theorem 1 (Ky Fan dominance theorem) The Inequality (2.13) holds for any unitarily invariant norm if and only if

(2.20)

Another useful tool is the following “rectangular” version of Cauchy interlacing theorem. For a proof of this result see ( [24] , p. 229) or ( [25] , p. 1250).

Theorem 2 (A rectangular Cauchy interlace theorem) Let the matrix have the singular values (2.2). Let the matrix be a submatrix of which is obtained by deleting rows and columns of. That is, and. Define and let

denote the singular values of. Then

(2.21)

To ease the coming discussions we return to square matrices. In the next assertions is an arbitrary real matrix. Combining the interlace theorem with the dominance theorem leads to the following corollary.

Theorem 3 Let the matrix be obtained from by setting to zero all the entries in the last rows and columns of. Then the inequality

(2.22)

holds for any unitarily invariant norm.

Theorem 4 Let the diagonal matrix

be obtained from the diagonal entries of. Then

(2.23)

in any unitarily invariant norm.

Proof. There is no loss of generality in assuming that the diagonal entries of are ordered such that

Let the matrix be defined as in Theorem 3. Then from (2.10) and (2.22) we conclude that

which proves (2.23).

Corollary 5 The diagonal matrix

satisfies

(2.24)

in any unitarily invariant norm.

Lemma 6 Let and be a pair of real symmetric matrices that satisfy

Then

in any unitarily invariant norm.

Proof. Using the spectral decomposition of it is possible to assume that is a diagonal matrix:

The matrix is positive semidefinite and, therefore, has non-negative diagonal entries. This observation implies the inequalities

and

while (2.23) gives

Theorem 7 (The pinching principle) Let the matrix be partitioned in the form

(2.25)

where and. Let the matrix

(2.26)

denote the “pinched” version of. Then the inequality

(2.27)

holds in any unitarily invariant norm.

Proof. Using the SVD of we obtain an pair of orthonormal matrices, and, such that

is a diagonal matrix that contains the singular values of. Similarly there exists a pair of orthonormal matrices, and, such that is a diagonal matrix that contains

the singular values of. The related matrices

are orthonormal matrices, and

(2.28)

is a diagonal matrix. Moreover, comparing with shows that

(2.29)

Hence a further use of (2.23) gives

Equality (2.28) relates the singular values of with those of the matrices and: Each singular value of is a singular value of. Similarly, each singular value of is a singular value of. Conversely, each singular value of is a singular value of or a singular value of. The last observation enables us to sharpen the results in certain cases. This is illustrated in Lemmas 8-11 below, which seem to be new. We will use these lemmas in the proofs of Theorems 18-21.

Lemma 8 (Pinching in Schatten p-norms)

(2.30)

Lemma 9 (Pinching in the trace norm)

(2.31)

Lemma 10 (Pinching in the spectral norm)

(2.32)

Lemma 11 (Pinching in Ky Fan k-norms) Let and be a pair of positive integers that satisfy

Then

(2.33)

Proof. The sum is formed from singular values of, while the sum defined by is composed from the largest singular values of.

The next tools consider the problem of approximating one matrix by another matrix of lower rank. Let by a given matrix with SVD that satisfies (2.1)-(2.8). Let be a given integer, and let

denote the related set of low-rank matrices. Then here we seek a matrix that is nearest to in a certain matrix norm. The difficulty stems from the fact that is not a convex set. Let denote a rank-k truncated SVD of as defined in (2.8). Then the Eckart-Young theorem [26] says that solves this problem in the Frobenius norm. The extension of this result to any unitarily invariant norm is due to Mirsky [27] . (Recall that is not always unique. In such cases the nearest matrix is not unique.) A detailed statement of these assertions is given below. For recent discussions and proofs see [25] .

Theorem 12 (Eckart-Young) The inequality

holds for any matrix. Moreover, the matrix solves the problem

giving the optimal value of

Theorem 13 (Mirsky) Let be any unitarily invariant norm on. Then the inequality

holds for any matrix. In other words, the matrix solves the problem

3. Positive Approximants of Symmetric Matrices

In this section we consider the solution of problem (1.3). Since is a unitarily invariant norm, the spectral decomposition (1.2) enables us to convert (1.3) into the simpler form

(3.1)

whose solution provides a solution of (1.3).

Theorem 14 Let the matrix be defined as in (1.5). Then solves (3.1) in any unitarily invariant norm.

Proof. Let the diagonal matrix be defined by the equality

That is

(3.2)

Let be some matrix in and let the matrix be defined by the equality

(3.3)

Then the proof is concluded by showing that

(3.4)

Let the diagonal matrix

(3.5)

be obtained from the last diagonal entries of. Then Corollary 5 implies that

(3.6)

On the other hand, since, the diagonal entries of are non-negative, which implies the inequalities

(3.7)

and

(3.8)

Now combining (3.6) and (3.8) gives (3.4)

Theorem 14 is not new, e.g. ( [8] , p. 277) and [9] . However, the current proof is simple and short. In the next sections we extend these arguments to derive low-rank approximants.

4. Low-Rank Positive Approximants in the Frobenius Norm

In this section we consider the solution of problem (1.1) in the Frobenius norm. As before, the spectral decom- position (1.2) can be used to “diagonalize” the problem and the actual problem to solve has the form

(4.1)

Theorem 15 Let the matrix be defined as in (1.6). Then this matrix solves (4.1)

Proof. Let the diagonal matrix be defined by the equality

That is,

(4.2)

and

(4.3)

Let be some matrix in and let the matrix be defined by the equality

(4.4)

Then the proof is concluded by showing that

(4.5)

This aim is achieved by considering a partition of and in the form

(4.6)

where and are matrices, while and are matrices. Then, clearly,

(4.7)

Also, as before, since is a positive semidefinite matrix it has non-negative diagonal entries, which implies the inequalities

(4.8)

and

(4.9)

It is left, therefore, to show that

(4.10)

Observe that the matrices and are related by the equality

(4.11)

where

(4.12)

and

(4.13)

Moreover, since is a principal submatrix of,

(4.14)

Hence from the Eckart-Young theorem we obtain that

(4.15)

Corollary 16 Let be a given real symmetric matrix with the spectral decomposition (1.2). Then the matrix

(4.16)

solves the problem

(4.17)

Corollary 17 Let be a given matrix, let the matrix have the spectral decomposition (1.2), and let the matrix be defined in (4.16). Then solves the problem

(4.18)

5. Low-Rank Positive Approximants in the Schatten p-Norm

Let the diagonal matrix be obtained from the spectral decomposition (1.2). In this section we consider the problem

(5.1)

Theorem 18 Let the matrix be defined in (1.6). Then this matrix solves (5.1)

Proof. Let the matrices, and be defined as in the proof of Theorem 15. Then here it is necessary to prove that

(5.2)

where

(5.3)

Let and be partitioned as in (4.6). Then from Lemma 8 we have

(5.4)

Now Theorem 4 and (4.8) imply

(5.5)

while applying Mirsky theorem on (4.11)-(4.14) gives

(5.6)

Finally substituting (5.5) and (5.6) into (5.4) gives (5.2).

6. Low-Rank Positive Approximants in the Trace Norm

Using the former notations, here we consider the problem

(6.1)

Theorem 19 The matrix solves (6.1).

Proof. It is needed to show that

(6.2)

where

(6.3)

The use of Lemma 9 yields

(6.4)

Here Theorem 4 and (4.8) imply the inequalities

(6.5)

and Mirsky theorem gives

(6.6)

which completes the proof.

7. Low-Rank Positive Approximants in the Spectral Norm

In this case we consider the problem

(7.1)

Theorem 20 The matrix solves (7.1).

Proof. Following the former notations and arguments, here it is needed to show that

Define

Then, clearly,

Using Lemma 10 we see that

Now Theorem 4 and (4.8) imply

while Mirsky theorem gives

8. Unitarily Invariant Norms

Let the diagonal matrices and be defined as in Section 1, and let denote any unitarily invariant norm on. Below we will show that solves the problem

(8.1)

The derivation of this result is based on the following assertion, which considers Ky Fan -norms.

Theorem 21 The matrix solves the problem

(8.2)

for.

Proof. We have already proved that solves (8.2) for the spectral norm and the trace norm. Hence it is left to consider the case when. As before, the diagonal matrix is defined in (4.2), and the matrices and satisfy (4.4) as well as the partition (4.6). With these notations at hand it is needed to show that

(8.3)

Let be partitioned in a similar way:

(8.4)

where

(8.5)

and

(8.6)

Then there are three different cases to consider.

The first case occurs when

(8.7)

Here Theorem 3 implies the inequalities

(8.8)

while from (4.11)-(4.14) and Mirsky theorem we obtain

(8.9)

which proves (8.3).

The second case occurs when

(8.10)

Here Theorem 3 implies

(8.11)

while Theorem 4 and the inequalities (4.8) give

(8.12)

which proves (8.3).

The third case occurs when neither (8.7) nor (8.10) hold. In this case there exist two positive integers, and, such that

(8.13)

and

(8.14)

Now Lemma 11 shows that

(8.15)

A further use of (4.11)-(4.14) and Mirsky theorem give

(8.16)

and from Theorem 4 and (4.8) we obtain

(8.17)

Hence by substituting (8.16) and (8.17) into (8.15) we get (8.3).

The fact that (8.3) holds for means that the inequality

(8.18)

holds for any unitarily invariant norm. This observation is a direct consequence of Ky Fan dominance theorem. The last inequality proves our final results.

Theorem 22 The matrix solves (8.1) in any unitarily invariant norm.

Theorem 23 Using the notations of Section 1, the matrix

solves (1.1) in any unitarily invariant norm.

9. Concluding Remarks

In view of Theorem 14 and Mirsky theorem, the observation that solves (8.1) is not surprising. However, as we have seen, the proof of this assertion is not straightforward. A key argument in the proof is the inequality (8.15), which is based on Lemma 11.

Once Theorem 22 is proved, it is possible to use this result to derive Theorems 15-18. Yet the direct proofs that we give clearly illustrate why these theorems work. In fact, the proof of Theorem 15 paves the way for the other proofs. Moreover, as Corollary 17 shows, when using the Frobenius norm we get stronger results: In this case we are able to compute a low-rank positive approximant of any matrix.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Dax, A. (2014) Imputing Missing Entries of a Data Matrix: A Review. Techical Report, Hydrological Service of Israel.
[2]	Trosset, M.W. (2000) Distance Matrix Completion by Numerical Optimization. Computational Optimization and Applications, 17, 11-22. http://dx.doi.org/10.1023/A:1008722907820
[3]	Higham, N.J. (1988) Computing a Nearest Symmetric Positive Semidefinite Matrix. Linear Algebra and Its Applications, 103, 103-118. http://dx.doi.org/10.1016/0024-3795(88)90223-6
[4]	Halmos, P.R. (1972) Positive Approximants of Operators. Indiana University Mathematics Journal, 21, 951-960. http://dx.doi.org/10.1512/iumj.1972.21.21076
[5]	Rogers, D.D. and Ward, J.D. (1981) Cp-Minimal Positive Approximants. Acta Scientiarum Mathematicarum, 43, 109-115.
[6]	Ando, T. (1985) Approximation in Trace Norm by Positive Semidefinite Matrices. Linear Algebra and Its Applications, 71, 15-21. http://dx.doi.org/10.1016/0024-3795(85)90230-7
[7]	Ando, T., Sekiguchi, T. and Suzuki, T. (1973) Approximation by Positive Operators. Mathematische Zeitschrift, 131, 273-282. http://dx.doi.org/10.1007/BF01174903
[8]	Bhatia, R. (1997) Matrix Analysis. Springer, New York. http://dx.doi.org/10.1007/978-1-4612-0653-8
[9]	Bhatia, R. and Kittaneh, F. (1992) Approximation by Positive Operators. Linear Algebra and Its Applications, 161, 1-9. http://dx.doi.org/10.1016/0024-3795(92)90001-Q
[10]	Bouldin, R. (1973) Positive Approximants. Transactions of the American Mathematical Society, 177, 391-403. http://dx.doi.org/10.1090/S0002-9947-1973-0317082-6
[11]	Sekiguchi, T. (1976) Positive Approximants of Normal Operators. Hokkaido Mathematical Journal, 5, 270-279. http://dx.doi.org/10.14492/hokmj/1381758677
[12]	Bouldin, R. (1980) Best Approximation of a Normal Operator in the Schatten p-Norm. Proceedings of the American Mathematical Society, 80, 277-282.
[13]	Bouldin, R. (1987) Best Approximation of a Normal Operator in the Trace Norm. Acta Scientiarum Mathematicarum, 51, 467-474.
[14]	Bouldin, R., (1988) Best Approximation of a Nonnormal Operator in the Trace Norm. Journal of Mathematical Analysis and Applications, 132, 102-113. http://dx.doi.org/10.1016/0022-247X(88)90046-7
[15]	Laszkiewicz, B. and Zietak, K. (2008) Approximation by Matrices with Restricted Spectra. Linear Algebra and Its Applications, 428, 1031-1040. http://dx.doi.org/10.1016/j.laa.2007.09.009
[16]	Phillips, J. (1977) Nearest Normal Approximation for Certain Normal Operators. Proceedings of the American Mathematical Society, 67, 236-240. http://dx.doi.org/10.1090/S0002-9939-1977-0458212-4
[17]	Ruhe, A. (1987) Closest Normal Matrix Finally Found! BIT Numerical Mathematics, 27, 585-598. http://dx.doi.org/10.1007/BF01937278
[18]	Zietak, K. (1997) Strict Spectral Approximation of a Matrix and Some Related Problems. Applicationes Mathematicae, 24, 267-280.
[19]	Higham, N.J. (1989) Matrix Nearness Problems and Applications. In: Gover, M.J.C. and Barnett, S., Eds., Applications of Matrix Theory, Oxford University Press, Oxford, 1-27.
[20]	Fan, K. (1951) Maximum Properties and Inequalities for the Eigenvalues of Completely Continuous Operators. Proceedings of the National Academy of Sciences of the United States of America, 37, 760-766. http://dx.doi.org/10.1073/pnas.37.11.760
[21]	Fan, K. and Hoffman, A.J. (1955) Some Metric Inequalities in the Space of Matrices. Proceedings of the American Mathematical Society, 6, 111-116. http://dx.doi.org/10.1090/S0002-9939-1955-0067841-7
[22]	Horn, R.A. and Johnson, C.R. (1991) Topics in Matrix Analysis. Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9780511840371
[23]	Marshall, A.W., Olkin, I. and Arnold, B.C. (2011) Inequalities: Theory of Majorization and Its Applications. Springer Series in Statistics, 2nd Edition, Springer, New York.
[24]	Zhang, F. (1999) Matrix Theory: Basic Results and Techniques. Springer-Verlag, New York. http://dx.doi.org/10.1007/978-1-4757-5797-2
[25]	Dax, A. (2010) On Extremum Properties of Orthogonal Quotient Matrices. Linear Algebra and Its Applications, 432, 1234-1257. http://dx.doi.org/10.1016/j.laa.2009.10.034
[26]	Eckart, C. and Young, G. (1936) The Approximation of One Matrix by Another of Lower Rank. Psychometrika, 1, 211-218. http://dx.doi.org/10.1007/BF02288367
[27]	Mirsky, L. (1960) Symmetric Gauge Functions and Unitarily Invariant Norms. Quarterly Journal of Mathematics, 11, 50-59. http://dx.doi.org/10.1093/qmath/11.1.50