1. Introduction
The two-dimensional (2d) Navier-Stokes system of partial differential equations (PDEs) for a Newtonian fluid with a constant density 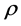 and a constant kinematic viscosity
and a constant kinematic viscosity 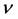 in a gravity field
in a gravity field 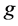 is
is
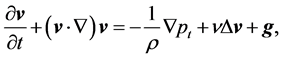 (1)
(1)
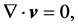 (2)
(2)
where 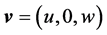 is a vector field of the flow velocity,
is a vector field of the flow velocity,  is a vector field of the gravitational acceleration,
is a vector field of the gravitational acceleration,  is a scalar field of the total pressure,
is a scalar field of the total pressure, 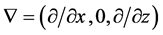 and
and 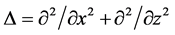 are the gradient and the Laplacian in the 2d Cartesian coordinate system
are the gradient and the Laplacian in the 2d Cartesian coordinate system 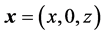 of the three-dimensional (3d) space with unit vectors
of the three-dimensional (3d) space with unit vectors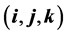 , respectively, and t is time.
, respectively, and t is time.
By a flow vorticity 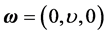 of the velocity field
of the velocity field
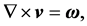 (3)
(3)
Equation (1) may be written into the Lamb-Pozrikidis form [1] [2]
 (4)
(4)
which sets a dynamic balance of inertial, potential, vortical, and viscous forces, respectively.
Using a dynamic pressure per unit mass [3]
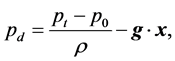 (5)
(5)
where ![]() is a reference pressure, a kinetic energy per unit mass
is a reference pressure, a kinetic energy per unit mass ![]() the 2d Helmholtz decomposition [4] of the velocity field
the 2d Helmholtz decomposition [4] of the velocity field
![]() (6)
(6)
and the vortex force
![]() (7)
(7)
Equation (4) is reduced to the Lamb-Helmholtz PDE [5]
![]() (8)
(8)
for a scalar Bernoulli potential and a vector Helmholtz potential, respectively,
![]() (9)
(9)
![]() (10)
(10)
where ![]() and d are scalar potentials,
and d are scalar potentials, ![]() and
and ![]() are vector potentials,
are vector potentials, ![]() and b are pseudovector potentials of
and b are pseudovector potentials of ![]() and
and![]() , respectively. The Lamb-Helmholtz PDE (8) means a dynamic balance between potential and vortical forces of the Navier-Stokes PDE (1), which are separated completely. Reduction of (1) to (8) means the potential-vortical duality of the Navier-Stokes PDE since writing equation (8) as
, respectively. The Lamb-Helmholtz PDE (8) means a dynamic balance between potential and vortical forces of the Navier-Stokes PDE (1), which are separated completely. Reduction of (1) to (8) means the potential-vortical duality of the Navier-Stokes PDE since writing equation (8) as
![]() (11)
(11)
shows that a virtual force ![]() of (1) may be represented both in the potential form
of (1) may be represented both in the potential form ![]() and the vortical form
and the vortical form![]() .
.
The exponential Fourier eigenfunctions obtained by the classical method of separation of variables of the 2d Laplace equation in [1] and [4] were primarily used for a linear part of the kinematic problem for free-surface waves of the theory of the ideal fluid with ![]() in [6] . This analytical method was recently developed into the computational method of solving PDEs by decomposition into invariant structures. Topological flows away from boundaries were computed by the Boussinesq-Rayleigh-Taylor structures in [3] . Spatiotemporal cascades of exposed and hidden perturbations of the Couette flow were modeled by the trigonometric Taylor structures and the trigonometric-hyperbolic structures, respectively, in [7] . Dual perturbations of the Poiseuille-Hagen flow were treated by the invariant trigonometric, hyperbolic, and elliptic structures in [8] . Exact solutions for the conservative interaction of N internal waves were recently obtained by experimental and theoretical computing with kinematic Fourier (KF) structures with space-dependent structural coefficients and exponential kinematic Fourier (KEF) structures, dynamic exponential Fourier (DEF) structures, and KEF-DEF structures with constant structural coefficients in [5] .
in [6] . This analytical method was recently developed into the computational method of solving PDEs by decomposition into invariant structures. Topological flows away from boundaries were computed by the Boussinesq-Rayleigh-Taylor structures in [3] . Spatiotemporal cascades of exposed and hidden perturbations of the Couette flow were modeled by the trigonometric Taylor structures and the trigonometric-hyperbolic structures, respectively, in [7] . Dual perturbations of the Poiseuille-Hagen flow were treated by the invariant trigonometric, hyperbolic, and elliptic structures in [8] . Exact solutions for the conservative interaction of N internal waves were recently obtained by experimental and theoretical computing with kinematic Fourier (KF) structures with space-dependent structural coefficients and exponential kinematic Fourier (KEF) structures, dynamic exponential Fourier (DEF) structures, and KEF-DEF structures with constant structural coefficients in [5] .
To examine linear and nonlinear parts of kinematic and dynamic problems for 2d stochastic waves in the theory of Newtonian flows with harmonic velocity, the KEF structures, the DEF structures, and the KEF-DEF structures with time-dependent structural coefficients are developed in the current paper. The structure of this paper is as follows. The KEF structures are used to compute theoretical solutions of the kinematic problems for the velocity components and the dual potentials of the velocity field in Section 2. The KEF and KEF-DEF structures are employed for theoretical computation of the dynamic problems for the Helmholtz and Bernoulli potentials, the kinetic energy, and the total pressure in Section 3. Verification of the experimental and theoretical solutions is also provided in Section 3. Various scenarios of a developed wave chaos are treated in Section 4. A summary of main results is given in Section 5.
2. Kinematic Problems for Internal Waves
The following solutions and admissible boundary conditions for the kinematic problems of Section 2 in the KEF and DEF structures with time-dependent coefficients were primarily computed via experimental programming techniques, which use lists of equations and expressions of Maple™ in the virtual environment of a global variable Eqs with 25 procedures of 600 code lines in total.
2.1. Formulation of Theoretical Kinematic Problems for the Velocity Field
Theoretical kinematic problems for harmonic velocity components ![]() and
and ![]() of a cumulative flow
of a cumulative flow ![]() of a Newtonian fluid are given by vanishing the y-component of the vorticity Equation (3) and the continuity Equation (2), respectively,
of a Newtonian fluid are given by vanishing the y-component of the vorticity Equation (3) and the continuity Equation (2), respectively,
![]() (12)
(12)
To consider a deterministic chaos of N internal, stochastic waves, the cumulative flow is decomposed into a superposition of local flows
![]() (13)
(13)
such that the local vorticity and continuity equations are
![]() (14)
(14)
where ![]()
An upper cumulative flow is specified by the Dirichlet condition in the KF structure on a lower boundary ![]() of an upper domain
of an upper domain ![]() and
and ![]() (see Figure 1).
(see Figure 1).
![]()
Figure 1. Configuration of upper and lower domains for stochastic waves.
![]() (15)
(15)
and a vanishing condition as ![]()
![]() (16)
(16)
A lower cumulative flow is identified by the Dirichlet condition on an upper boundary ![]() of a lower domain
of a lower domain![]() and
and ![]() (see Figure 1).
(see Figure 1).
![]() (17)
(17)
and a vanishing condition as ![]()
![]() (18)
(18)
Thus, an effect of surface waves on the internal waves is described by the Dirichlet conditions (15) and (17). Here, a structural notation
![]() (19)
(19)
is used for kinematic structural functions ![]() and
and![]() , where
, where ![]() and
and ![]() are time-dependent boundary functions,
are time-dependent boundary functions, ![]() is an argument of the kinematic and dynamic structural functions,
is an argument of the kinematic and dynamic structural functions, ![]() is a propagation variable,
is a propagation variable, ![]() is a wave number,
is a wave number, ![]() is a celerity, and
is a celerity, and ![]() is an initial coordinate for all n. Similar to [5] , boundary conditions for
is an initial coordinate for all n. Similar to [5] , boundary conditions for ![]() are then redundant since boundary parameters of
are then redundant since boundary parameters of ![]() depend on boundary parameters of
depend on boundary parameters of ![]() for the upper and lower flows, respectively, as
for the upper and lower flows, respectively, as
![]() (20)
(20)
![]() (21)
(21)
Similarly to w, u vanishes as ![]()
![]() (22)
(22)
for the upper and lower cumulative flows, respectively.
2.2. Theoretical Solutions for the Velocity Field
Theoretical solutions of kinematic problems (12)-(18) are constructed in the KEF structure ![]() of two spatial variables x, u and time t with a general term
of two spatial variables x, u and time t with a general term![]() , which in the structural notation may be written as
, which in the structural notation may be written as
![]() (23)
(23)
where signs “−” and “+” of the exponential term refer to the upper and lower flows, respectively, first letters f and g of structural coefficients ![]() and
and ![]() refer to the kinematic structural functions
refer to the kinematic structural functions![]() ,
, ![]() and a second letter to the expanded variable p. General terms of the velocity components of the upper and lower flows become, respectively,
and a second letter to the expanded variable p. General terms of the velocity components of the upper and lower flows become, respectively,
![]() (24)
(24)
![]() (25)
(25)
It may be shown that spatial derivatives of ![]() are
are
![]() (26)
(26)
![]() (27)
(27)
Application of (26) (27) to (24) (25), substitution in (14), collection of the structural functions, and vanishing their coefficients reduce two vorticity and continuity PDEs to the following system of four vorticity and continuity algebraic equations (AEs) with respect to ![]() for the upper flows
for the upper flows
![]() (28)
(28)
![]() (29)
(29)
the lower flows
![]() (30)
(30)
![]() (31)
(31)
and all ![]()
Solving AEs (28) and (30) yields for the upper and lower flows, respectively,
![]() (32)
(32)
![]() (33)
(33)
Substitution of solutions (32) in (29) and (33) in (31) reduces them to identities, showing that vorticity and continuity AEs (28)-(31) are compatible. Finally, substitution of (32) (33) in the KEF structures (24) (25) and solving the Dirichlet boundary conditions (15) and (17) with respect to ![]() and
and ![]() produces velocity components for the upper and lower cumulative flow, respectively,
produces velocity components for the upper and lower cumulative flow, respectively,
![]() (34)
(34)
while vanishing boundary conditions (16) and (18) are obviously satisfied.
2.3. The DEF Structure and Theoretical Jacobian Determinants of the Velocity Field
Define two KEF structures ![]() and
and ![]() with general terms
with general terms ![]() and
and ![]() by using the generalized Einstein notation for summation that is extended for exponents in [5]
by using the generalized Einstein notation for summation that is extended for exponents in [5]
![]() (35)
(35)
Following [5] , define structural functions![]() , and
, and ![]() of the DEF structure
of the DEF structure
![]() (36)
(36)
where capital letters C and S stand for dynamic structural functions cosine and sine, letter a for arguments![]() ,
, ![]() , letters s and d for sum and difference of arguments
, letters s and d for sum and difference of arguments ![]() and
and![]() .
.
Computation of a general term ![]() by summation of diagonal terms yields
by summation of diagonal terms yields
![]() (37)
(37)
A general term ![]() computed by rectangular summation of non-diagonal terms becomes
computed by rectangular summation of non-diagonal terms becomes
![]() (38)
(38)
By triangular summation, ![]() is reduced to
is reduced to
![]() (39)
(39)
By (37) and (39), summation formula for the product of the KEF structures may be written as the DEF structure with time-dependent structural coefficients
![]() (40)
(40)
with the following structural coefficients:
![]() (41)
(41)
where first two letters![]() , and
, and ![]() of structural coefficients
of structural coefficients![]() , and
, and ![]() stand for dynamic structural functions
stand for dynamic structural functions![]() , and
, and![]() , respectively, and a third letter for variable p.
, respectively, and a third letter for variable p.
Computation of local JDs for the velocity components of the upper and lower flow, respectively, yields
![]() (42)
(42)
Thus, velocity components ![]() and
and ![]() are independent for non-trivial structural coefficients
are independent for non-trivial structural coefficients ![]() and
and![]() since the local JDs vanish when
since the local JDs vanish when![]() .
.
Computation of a global JD by using (40) (41) for velocity components of the upper and lower cumulative flows (34) with slant internal waves gives
![]() (43)
(43)
So, ![]() is a superposition of a propagation JD with general term
is a superposition of a propagation JD with general term ![]() proportional to
proportional to![]() , an interaction JD with
, an interaction JD with ![]() proportional to
proportional to![]() , and an interaction JD with
, and an interaction JD with ![]() proportional to
proportional to![]() , which describe interaction between parallel and orthogonal internal waves, respectively.
, which describe interaction between parallel and orthogonal internal waves, respectively.
![]() coincides with local JDs (42). They describe propagation of internal waves and vanish only for vanishing waves with
coincides with local JDs (42). They describe propagation of internal waves and vanish only for vanishing waves with![]() .
. ![]() vanishes for parallel waves with
vanishes for parallel waves with
![]() (44)
(44)
Global JD (43) then becomes
![]() (45)
(45)
Thus, the global JD does not vanish for parallel waves with non-vanishing![]() .
.
![]() vanishes for orthogonal waves with
vanishes for orthogonal waves with
![]() (46)
(46)
In this case, global JD (43) is reduced to
![]() (47)
(47)
So, the global JD does not vanish also for orthogonal waves with non-vanishing ![]() In the general case of slant internal waves (43), both
In the general case of slant internal waves (43), both ![]() and
and ![]() are non-vanishing. Therefore, both propagating and interacting waves are independent for structural coefficients with
are non-vanishing. Therefore, both propagating and interacting waves are independent for structural coefficients with ![]() for all n.
for all n.
2.4. Theoretical Solutions for the Kinematic Potentials in the KEF Structures
Theoretical kinematic problems for cumulative pseudovector potential ![]() and cumulative scalar potential
and cumulative scalar potential ![]() of
of ![]() are set by the global Helmholtz PDEs (6)
are set by the global Helmholtz PDEs (6)
![]() (48)
(48)
![]() (49)
(49)
since the potential-vortical duality the velocity field admits two presentations: ![]() for
for ![]() and
and![]() for
for![]() . The cumulative kinematic potentials are decomposed into a superposition of local kinematic potentials
. The cumulative kinematic potentials are decomposed into a superposition of local kinematic potentials
![]() (50)
(50)
such that the local Helmholtz PDEs are
![]() (51)
(51)
![]() (52)
(52)
where![]() .
.
Construct general terms of the kinematic potentials of the local flows in the KEF structure with time-depen- dent coefficients
![]() (53)
(53)
![]() (54)
(54)
Application of (26) (27) to (53) (54), substitution in the Helmholtz PDEs (51) (52), collection of the structural functions, and vanishing their coefficients reduce four Helmholtz PDEs to the following system of eight Helmholtz AEs for the upper flows
![]() (55)
(55)
![]() (56)
(56)
the lower flows
![]() (57)
(57)
![]() (58)
(58)
and all![]() , and
, and![]() .
.
Solving AEs (55) and (57) with respect to time-dependent structural coefficients![]() , and
, and ![]() gives for the upper and lower flows, respectively,
gives for the upper and lower flows, respectively,
![]() (59)
(59)
Substitution of solutions (59) in AEs (56) and (58) reduces them to identities. Finally, substitution of structural coefficients (59) in the KEF structures (53) (54) and superpositions (50) yields the cumulative kinematic potentials in the KEF structures for the upper and lower cumulative flows, respectively,
![]() (60)
(60)
The theoretical solutions in the KEF and DEF structures for the kinematic problems of Section 2 were computed utilizing theoretical programming methods with symbolic general terms in the virtual environment of a global variable Eqt with 21 procedures of 522 Maple code lines in total. The theoretical formulas for velocity components (34), the products of the KEF structures (40) (41), and the kinematic potentials (60) of the upper and lower cumulative flows were justified by the correspondent experimental solutions for N = 1, 3, 10.
3. Dynamic Problems for Internal Waves
The following solutions for the dynamic problems of Section 3 in the KEF, DEF, and KEF-DEF structures were primarily computed by experimental programming with lists of equations and expressions in the virtual environment of the global variable Eqs with 18 procedures of 470 code lines in total.
3.1. Theoretical Solutions for the Dynamic Potentials in the KEF Structures
Theoretical dynamic problems in the KF structures for the Helmholtz and Bernoulli potentials of the cumulative flows are set by the Lamb-Helmholtz PDEs (8)-(10) in the vortical presentation with ![]()
![]() (61)
(61)
Equations (61) are complemented by the local Lamb-Helmholtz PDEs
![]() (62)
(62)
since the cumulative dynamic potentials are again decomposed into the local dynamic potentials
![]() (63)
(63)
Construct a general term of the Bernoulli potential of the local flows in the KEF structure with time-depen- dent coefficients
![]() (64)
(64)
Computation of the temporal derivative of![]() , application of (26) (27), substitution in (62), collection of the structural functions, and vanishing their coefficients reduce two Lamb-Helmholtz PDEs to the following system of four Lamb-Helmholtz AEs with respect to
, application of (26) (27), substitution in (62), collection of the structural functions, and vanishing their coefficients reduce two Lamb-Helmholtz PDEs to the following system of four Lamb-Helmholtz AEs with respect to ![]() and
and ![]() for the upper flows
for the upper flows
![]() (65)
(65)
![]() (66)
(66)
and the lower flows
![]() (67)
(67)
![]() (68)
(68)
and all variables, parameters, and functions![]() , and
, and![]() .
.
Solving AEs (65) and (67) for structural coefficients ![]() and
and ![]() yields for the upper and lower flows, respectively,
yields for the upper and lower flows, respectively,
![]() (69)
(69)
Substitution of solutions (69) in AEs (66) and (68) reduces them to identities. Eventually, substitution of structural coefficients (69) in the KEF structure (64) and superpositions (63) returns the cumulative dynamic potentials in the KEF structures for the upper and lower cumulative flows, respectively,
![]() (70)
(70)
![]() (71)
(71)
3.2. Theoretical Solutions for the Total Pressure in the KEF-DEF Structures
Theoretical dynamic problems in the KEF-DEF structures for![]() ,
, ![]() , and
, and ![]() of the cumulative flows are formulated by definition
of the cumulative flows are formulated by definition
![]() (72)
(72)
the Bernoulli Equation (9) with ![]()
![]() (73)
(73)
and the hydrostatic Equation (5)
![]() (74)
(74)
where ![]() is the reference pressure at
is the reference pressure at ![]()
Computation of ![]() by (40) (41) and (34) returns
by (40) (41) and (34) returns
![]() (75)
(75)
for the upper and lower cumulative flows, respectively. Substitution of (71), (75), and (73) in (74) yields
![]() (76)
(76)
for the upper and lower cumulative flows, respectively. So, the kinetic energy is obtained in the DEF structures, the dynamic pressure is expressed in the KEF-DEF structures, and the total pressure is computed in the KEF-DEF and polynomial structures.
3.3. Harmonic Relationships between the Kinematic and Dynamic Variables
Similar to the invariant trigonometric, hyperbolic, and elliptic structures [8] , there are two pairs of independent KEF structures: generating structures with general terms![]() ,
, ![]() and complementary structures with general terms
and complementary structures with general terms![]() ,
, ![]() for the upper and lower flows, respectively,
for the upper and lower flows, respectively,
![]() (77)
(77)
![]() (78)
(78)
Expressing velocity components (34), kinematic potentials (60), and dynamic potentials (70) (71) through the generating and complementary structures (77) (78) and solving for ![]() and
and ![]() gives algebraic relationships
gives algebraic relationships
![]() (79)
(79)
Taking derivatives of (34) and (60) with respect to x, z and solving for ![]() and
and ![]() yields differential relationships, which extend algebraic ones (79),
yields differential relationships, which extend algebraic ones (79),
![]() (80)
(80)
In fluid dynamics, relationships (79) (80) mean that a harmonic flow, which is non-uniform in ![]() or
or ![]() directions, produces a complementary flow in z- or x-directions, respectively.
directions, produces a complementary flow in z- or x-directions, respectively.
Computing velocity components (34) and dynamic potentials (70) (71) through the generating and complementary structures (77) (78), taking temporal and spatial derivatives, and solving for ![]() and
and ![]() returns
returns
![]() (81)
(81)
Differential relationships (81) mean that spatial derivatives of the dynamic potentials generate temporal rates of a harmonic flow.
By the following substitutions:
![]() (82)
(82)
both local and global vorticity and continuity Equations (12) and (14), Helmholtz Equations (48)-(49) and (51)- (52), and Lamb-Helmholtz Equations (61) and (62), respectively, are reduced to the Cauchy-Riemann equations
![]() (83)
(83)
for conjugate functions ![]() and
and ![]() [4] . All conjugate functions have orthogonal isocurves, due to the vanishing scalar product of gradients,
[4] . All conjugate functions have orthogonal isocurves, due to the vanishing scalar product of gradients,
![]() (84)
(84)
and vanishing Laplacians,
![]() (85)
(85)
Thus, ![]() , and
, and ![]() are six pairs of harmonic functions with orthogonal isocurves.
are six pairs of harmonic functions with orthogonal isocurves.
3.4. Theoretical Verification by the System of Navier-Stokes PDEs
The system of the Navier-Stokes PDEs (1)-(2) in the scalar notation becomes
![]() (86)
(86)
![]() (87)
(87)
Computation of spatial derivatives of (34) by (26)-(27) reduces (87) to identity both for the upper and lower cumulative flows.
Temporal derivatives of ![]() in the KEF structures for the upper and lower cumulative flows, respectively, are
in the KEF structures for the upper and lower cumulative flows, respectively, are
![]() (88)
(88)
![]() (89)
(89)
The directional derivatives of (86) computed by (40)-(41) in the DEF structures for the upper and lower cumulative flows, respectively, become
![]() (90)
(90)
![]() (91)
(91)
By using (26)-(27), components of the gradient of (76) may be written in the KEF-DEF structures for the upper and lower cumulative flows, respectively, as
![]() (92)
(92)
![]() (93)
(93)
Substitution of Equations (88)-(93) and (85) for u and w in (86) reduces then to identities. Thus, Equations (34) and (76) constitute exact solutions in the KEF, DEF, and KEF-DEF structures with time-dependent structural coefficients for deterministic chaos of N stochastic waves both in the upper and lower domains.
The theoretical solutions in the KEF, DEF, and KEF-DEF structures for the dynamic problems of Section 3 were computed by theoretical programming methods with symbolic general terms in the virtual environment of the global variable Eqt with 14 procedures of 410 code lines in total. The theoretical solutions for Helmholtz and Bernoulli potentials (70)-(71), total pressure (76), temporal derivatives (88)-(89), directional derivatives (90)- (91), and pressure gradient (92)-(93) of the upper and lower cumulative flows were justified by the correspondent experimental solutions for N = 1, 3, 10.
All kinematic solutions of Section 2 and dynamic solutions of Section 3 with time-dependent structural coefficients are reduced to the correspondent solutions of [5] when ![]() and
and![]() .
.
4. Chaotic Scenarios
Boundary functions ![]() and
and![]() , which are shown in Figure 2 for
, which are shown in Figure 2 for![]() , are constructed from stochastic solutions of the Navier-Stokes equation in one dimension by the following method. Let
, are constructed from stochastic solutions of the Navier-Stokes equation in one dimension by the following method. Let ![]() and
and ![]() be the stochastic solutions of
be the stochastic solutions of
![]()
![]()
Figure 2. Stochastic boundary functions.
![]() (94)
(94)
where ![]() is the Reynolds number.
is the Reynolds number.
In agreement with [7] , ![]() is composed of an invariant structure with even indices of hyperbolic secant-tangent temporal modes and trigonometric sine spatial modes (HETO structure) and an invariant structure of the same temporal modes combined with trigonometric cosine spatial modes (HETE structure)
is composed of an invariant structure with even indices of hyperbolic secant-tangent temporal modes and trigonometric sine spatial modes (HETO structure) and an invariant structure of the same temporal modes combined with trigonometric cosine spatial modes (HETE structure)
![]() (95)
(95)
![]() is formed of an invariant structure with odd indices of hyperbolic secant-tangent temporal modes and trigonometric sine spatial modes (HOTO structure) and an invariant structure of the same temporal modes composed with trigonometric cosine spatial modes (HOTE structure)
is formed of an invariant structure with odd indices of hyperbolic secant-tangent temporal modes and trigonometric sine spatial modes (HOTO structure) and an invariant structure of the same temporal modes composed with trigonometric cosine spatial modes (HOTE structure)
![]() (96)
(96)
Here, a structural notation
![]() (97)
(97)
is used for structural functions of temporal and spatial modes, where ![]() is an index of spatiotemporal components,
is an index of spatiotemporal components, ![]() is an index of temporal modes,
is an index of temporal modes, ![]() is an index of spatial modes,
is an index of spatial modes, ![]() is a frequency,
is a frequency, ![]() is a delay parameter,
is a delay parameter, ![]()
![]()
![]() , and
, and ![]() are spatial amplitudes. Structural coefficients
are spatial amplitudes. Structural coefficients ![]()
![]()
![]() , and
, and ![]() are computed by initialization conditions
are computed by initialization conditions
![]() (98)
(98)
and recurrent relations
![]() (99)
(99)
In Figure 2, stochastic boundary functions
![]() (100)
(100)
were evaluated for![]() ,
, ![]() ,
, ![]() , temporal delays
, temporal delays![]() , a scale of temporal delays
, a scale of temporal delays![]() ,
, ![]() , scales of spatiotemporal components
, scales of spatiotemporal components
![]() (101)
(101)
and spatial amplitudes
![]() (102)
(102)
which insure convergence of the spatial modes. Frequencies of![]() :
:
![]()
and frequencies of![]() :
:
![]()
were computed by iterations from tolerance equations
![]() (103)
(103)
These equations guarantee that absolute values of remainders of the structural approximations of (94)
![]() (104)
(104)
![]() (105)
(105)
do not exceed ![]() for all
for all![]() , and
, and![]() , where
, where ![]() is an admissible error of computation of an invariant structure. Chaotic behavior of the boundary functions increases with n, K, and, especially,
is an admissible error of computation of an invariant structure. Chaotic behavior of the boundary functions increases with n, K, and, especially, ![]() , while various chaotic scenarios are modeled by
, while various chaotic scenarios are modeled by ![]() parameters
parameters![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and![]() .
.
The KEF structures and KEF-DEF structures are visualized in Figure 3 by instantaneous 3d surface plots with isocurves at ![]() for scalar potential
for scalar potential ![]() (60) and the dynamic pressure
(60) and the dynamic pressure
![]() with pt from (76), respectively. Local minimums of the KEF-DEF structure for pd coincides with local maximums of the DEF structure for
with pt from (76), respectively. Local minimums of the KEF-DEF structure for pd coincides with local maximums of the DEF structure for![]() , in agreement with [1] . The spatial structure of
, in agreement with [1] . The spatial structure of ![]() and pd for stochastic waves coincides with that shown in Figure 2 and Figure 3 of [5] for conservative
and pd for stochastic waves coincides with that shown in Figure 2 and Figure 3 of [5] for conservative
![]()
![]()
Figure 3. Scalar potential (left) and dynamic pressure (right) of the lower cumulative flow.
waves. The temporal structure of ![]() and pd for stochastic waves, which is visualized by animations, significantly differs from that of
and pd for stochastic waves, which is visualized by animations, significantly differs from that of ![]() and pd for conservative waves because of the chaotic behavior of boundary functions
and pd for conservative waves because of the chaotic behavior of boundary functions ![]() and
and![]() .
.
5. Conclusions
The computational method of solving PDEs by decomposition in invariant structures, which continues the analytical methods of separation of variables and undetermined coefficients, is generalized in the current paper at the KEF, DEF, and KEF-DEF structures with time-dependent coefficients. This computational method is implemented in the kinematic and dynamic problems for internal waves by 43 procedures with 1070 code lines of the experimental computing in total and 35 procedures with 932 code lines of the theoretical computing in total. These structures with time-dependent structural coefficients are invariant with respect to various differential and algebraic operations.
For internal waves vanishing at infinity in the upper and lower domains, the Dirichlet problems are formulated for the kinematic and dynamic systems of the vorticity, continuity, Helmholtz, Lamb-Helmholtz, and Bernoulli equations. The exact solutions of the Navier-Stokes PDEs for the deterministic chaos of N stochastic waves are revealed experimentally, proved theoretically, and justified by the system of Navier-Stokes PDEs in the class of flows with the harmonic velocity field. The kinematic and dynamic solutions for stochastic waves coincide with the correspondent solutions for conservative waves [5] when stochastic boundary functions are reduced to constants.
Independence of both propagating and interacting internal waves is shown by computation of the Jacobian determinants in the DEF structures. Conditions for existence of parallel and orthogonal waves with time-de- pendent amplitudes are obtained through the Jacobian determinants, as well. The harmonic relationships between six pairs of the harmonic, fluid-dynamic variables, their temporal derivatives, and their spatial derivatives with respect to x and z are derived both for the upper and lower flows.
The stochastic boundary functions are constructed from the stochastic solutions of the one-dimensional Navier-Stokes equation [7] with hyperbolic temporal modes and trigonometric spatial modes in the HETO, HETE, HOTO, and HOTE structures. Various scenarios of a developed wave chaos are modeled by 3N parameters for internal waves and 2N stochastic boundary functions, which depend on ![]() parameters, where K is a number of temporal modes.
parameters, where K is a number of temporal modes.
Acknowledgements
The author thanks S. P. Bhavaraju for the stimulating discussion at the 2013 SIAM Annual Meeting. Support of the College of Mount Saint Vincent and CAAM is gratefully acknowledged.