1. Introduction
A. Bejancu defined and studied  -submanifolds of a Kaehler manifold [1] . Later on,
-submanifolds of a Kaehler manifold [1] . Later on,  -submanifolds of a Sasakian manifold were studied by M. Kobayashi [2] , K. Yano and M. Kon [3] . J. A. Oubina introduced a new class of almost contact metric manifold known as trans-Sasakian manifold [4] . This class contains
-submanifolds of a Sasakian manifold were studied by M. Kobayashi [2] , K. Yano and M. Kon [3] . J. A. Oubina introduced a new class of almost contact metric manifold known as trans-Sasakian manifold [4] . This class contains 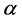 -Sasakian and
-Sasakian and  -Kenmotsu manifold [5] .
-Kenmotsu manifold [5] . 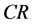 -submanifolds of a Kenmotsu manifold were studied by A. Bejancu and N. Papaghuic [6] . Geometry of
-submanifolds of a Kenmotsu manifold were studied by A. Bejancu and N. Papaghuic [6] . Geometry of  -submanifolds of a trans-Sasakian manifold have been studied by M. H. Shahid in [7] [8] .
-submanifolds of a trans-Sasakian manifold have been studied by M. H. Shahid in [7] [8] .  -submanifolds of a nearly trans-Sasakian manifold were studied by Falleh R. Al-Solamy [9] .
-submanifolds of a nearly trans-Sasakian manifold were studied by Falleh R. Al-Solamy [9] .  - submanifolds of an
- submanifolds of an  -Sasakian manifold with a semi-symmetric metric connection were studied by M. Ahmad et al. [10] . Motivated by the studies in [11] -[13] , in this paper we study
-Sasakian manifold with a semi-symmetric metric connection were studied by M. Ahmad et al. [10] . Motivated by the studies in [11] -[13] , in this paper we study  -submanifolds of a nearly transSasakian manifold endowed with a semi symmetric non-metric connection.
-submanifolds of a nearly transSasakian manifold endowed with a semi symmetric non-metric connection.
Let  be a linear connection in an
be a linear connection in an 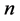 -dimensional differentiable manifold
-dimensional differentiable manifold . The torsion tensor
. The torsion tensor 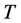 of
of 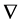 is given by
is given by

The connection  is symmetric if torsion tensor
is symmetric if torsion tensor  vanishes, otherwise it is non-symmetric. The connection
vanishes, otherwise it is non-symmetric. The connection  is metric connection if there is a Riemannian metric
is metric connection if there is a Riemannian metric  in
in 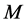 such that
such that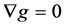 , otherwise it is non-metric. It is well known that a linear connection is symmetric and metric if and only if it is the Levi-Civita connection.
, otherwise it is non-metric. It is well known that a linear connection is symmetric and metric if and only if it is the Levi-Civita connection.
In [14] , S. Golab introduced the idea of a semi-symmetric and quarter symmetric linear connections. A linear connection  is said to be semi-symmetric if its torsion tensor
is said to be semi-symmetric if its torsion tensor  is of the form
is of the form

where  is a 1-form and
is a 1-form and 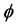 is a tensor field of the type (1,1).
is a tensor field of the type (1,1).
We consider integrabilities of horizontal and vertical distributions of  -submanifolds with a semi symmetric non-metric connection. We also consider parallel horizontal distributions of
-submanifolds with a semi symmetric non-metric connection. We also consider parallel horizontal distributions of  -submanifolds.
-submanifolds.
The paper is organized as follows: In Section 2, we recall some necessary details of nearly trans-Sasakian manifold. In Section 3, we study  -submanifolds of a nearly trans-Sasakian manifold. In Section 4, some useful lemmas are proved. In Section 5, some basic results on parallel distribution are investigated. In Section 6, we calculated Nijenhuis tensor and studied integrability conditions of the distributions on
-submanifolds of a nearly trans-Sasakian manifold. In Section 4, some useful lemmas are proved. In Section 5, some basic results on parallel distribution are investigated. In Section 6, we calculated Nijenhuis tensor and studied integrability conditions of the distributions on  -submanifolds of a nearly trans-Sasakian manifold with a semi symmetric non-metric connection.
-submanifolds of a nearly trans-Sasakian manifold with a semi symmetric non-metric connection.
2. Nearly Trans-Sasakian Manifold
Let  be an
be an  -dimensional almost contact metric manifold [15] with an almost contact metric structure
-dimensional almost contact metric manifold [15] with an almost contact metric structure , that is,
, that is,  is a (1,1) tensor field,
is a (1,1) tensor field,  is a vector field,
is a vector field,  is a 1-form and
is a 1-form and  is a compatible Riemannian metric such that
is a compatible Riemannian metric such that
 (1)
(1)
 (2)
(2)
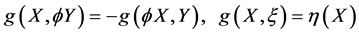 (3)
(3)
for all vector fields ,
, . There are two well known classes of almost contact metric manifolds, namely Sasakian and Kenmotsu manifolds. Sasakian manifolds are characterized by the tensorial relation
. There are two well known classes of almost contact metric manifolds, namely Sasakian and Kenmotsu manifolds. Sasakian manifolds are characterized by the tensorial relation

while Kenmotsu manifolds are given by the tensor equation
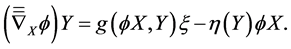
An almost contact metric structure  on
on  is called a trans-Sasakian structure [4] if
is called a trans-Sasakian structure [4] if  belongs to the class
belongs to the class  of Gray-Hervella classification of almost Hermitian manifolds [16] , where
of Gray-Hervella classification of almost Hermitian manifolds [16] , where  is the almost complex structure on
is the almost complex structure on  defined by
defined by

for all vector fields  on
on  and smooth function
and smooth function  on
on . This may be expressed by the condition [17]
. This may be expressed by the condition [17]
 (4)
(4)
for some smooth functions  and
and  on
on  and we say that the trans-Sasakian structure is of type
and we say that the trans-Sasakian structure is of type .
.
In 2000, C. Gherghe [18] introduced a nearly trans-Sasakian structure of the type  An almost contact metric structure
An almost contact metric structure 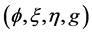 on
on  is called a nearly trans-Sasakian structure [18] if
is called a nearly trans-Sasakian structure [18] if
 (5)
(5)
A trans-Sasakian structure is always a nearly trans-Sasakian structure. Moreover, a nearly trans-Sasakian structure of type  is nearly Sasakian [19] .
is nearly Sasakian [19] .
Let  be an
be an 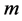 -dimensional isometrically immersed submanifold of a nearly trans-Sasakian manifold
-dimensional isometrically immersed submanifold of a nearly trans-Sasakian manifold  and denote by the same
and denote by the same  the Riemannian metric tensor field induced on
the Riemannian metric tensor field induced on  from that of
from that of .
.
3.  -Submanifolds of Nearly Trans-Sasakian Manifolds
-Submanifolds of Nearly Trans-Sasakian Manifolds
Definition 3.1 An  -dimensional Riemannian submanifold
-dimensional Riemannian submanifold  of a nearly trans-Sasakian manifold
of a nearly trans-Sasakian manifold  is called a
is called a  -submanifold if
-submanifold if  is tangent to
is tangent to 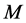 and there exists on
and there exists on  a differentiable distribution
a differentiable distribution 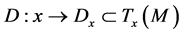 such that
such that
(i) the distribution  is invariant under
is invariant under , i.e.,
, i.e.,  for each
for each ;
;
(ii) The orthogonal complementary distribution  of the distribution
of the distribution  on
on  is antiinvarient under
is antiinvarient under , i.e.,
, i.e.,  for all
for all , where
, where  and
and  are tangent space and normal space of
are tangent space and normal space of  at
at  respectively.
respectively.
If dim  (resp.,
(resp., ), then
), then  -submanifold is called an invariant (resp., anti-invariant). The distribution
-submanifold is called an invariant (resp., anti-invariant). The distribution  (resp.,
(resp., ) is called the horizontal (resp., vertical) distribution. The pair
) is called the horizontal (resp., vertical) distribution. The pair  is called
is called  -horizontal (resp.,
-horizontal (resp.,  -invariant) if
-invariant) if  (resp.,
(resp., ) for
) for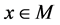 .
.
For any vector field  tangent to
tangent to , we put
, we put
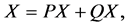 (6)
(6)
where  and
and  belong to the distribution
belong to the distribution  and
and 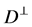 respectively.
respectively.
For any vector field  normal to
normal to , we put
, we put
 (7)
(7)
where  (resp.,
(resp., ) denotes the tangential (resp., normal) component of
) denotes the tangential (resp., normal) component of .
.
Now, we remark that owing to the existence of the 1-form , we can define a semi symmetric non-metric connection
, we can define a semi symmetric non-metric connection  in any almost contact metric manifold by
in any almost contact metric manifold by
 (8)
(8)
such that  for any
for any , where
, where  is the induced connection with respect to
is the induced connection with respect to  on
on .
.
By using (4) and (8), we get
 (9)
(9)
Similarly, we have

On adding above equations, we obtain
 (10)
(10)
This is the condition for  with a semi symmetric non-metric connection to be nearly transSasakian manifold.
with a semi symmetric non-metric connection to be nearly transSasakian manifold.
We denote by  the metric tensor of
the metric tensor of  as well as that induced on
as well as that induced on . Let
. Let  be the semi symmetric non-metric connection on
be the semi symmetric non-metric connection on  and
and  be the induced connection on
be the induced connection on  with respect to the unit normal
with respect to the unit normal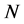 . Then we have:
. Then we have:
Theorem 3.2 (i) If  is
is  -horizontal,
-horizontal,  and
and  is parallel with respect to
is parallel with respect to , then the connection induced on a
, then the connection induced on a  -submanifold of a nearly trans-Sasakian manifold with a semi symmetric non-metric connection is also a semi symmetric non-metric connection.
-submanifold of a nearly trans-Sasakian manifold with a semi symmetric non-metric connection is also a semi symmetric non-metric connection.
(ii) If 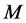 is
is  -vertical,
-vertical,  and
and  is parallel with respect to
is parallel with respect to , then the connection induced on a
, then the connection induced on a  -submanifold of a nearly trans-Sasakian with a semi symmetric non-metric connection is also a semi symmetric non-metric connection.
-submanifold of a nearly trans-Sasakian with a semi symmetric non-metric connection is also a semi symmetric non-metric connection.
(iii) The Gauss formula with respect to the semi symmetric non-metric connection is of the form
 .
.
Proof. Let  be the induced connection with respect to the unit normal
be the induced connection with respect to the unit normal  on a
on a  -submanifold of a nearly trans-Sasakian manifold from a semi symmetric non-metric connection connection
-submanifold of a nearly trans-Sasakian manifold from a semi symmetric non-metric connection connection , then
, then
 (11)
(11)
where  is a tensor field of the type (0,2) on
is a tensor field of the type (0,2) on  -submanifold
-submanifold . If
. If 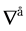 be the induced connection on
be the induced connection on 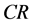 -submanifold from Riemannian connection
-submanifold from Riemannian connection , then
, then
 (12)
(12)
where  is a second fundamental form. By the definition of the semi symmetric non-metric connection, we have
is a second fundamental form. By the definition of the semi symmetric non-metric connection, we have

Now, using (11) and (12) in above equation, we have

Using (6), the above equation can be written as
 (13)
(13)
From (13), comparing the tangential and normal components from both the sides, we get
 (14)
(14)
 (15)
(15)
 (16)
(16)
Using (14), the Gauss formula for a  -submanifold of a nearly trans-Sasakian manifold with a semi symmetric non-metric connection is
-submanifold of a nearly trans-Sasakian manifold with a semi symmetric non-metric connection is
 (17)
(17)
This proves (iii). In view of (15), if  is
is  -horizontal,
-horizontal,  and
and  is parallel with respect to
is parallel with respect to , then the connection induced on a
, then the connection induced on a  -submanifold of a nearly trans-Sasakian manifold with a semi symmetric non-metric connection is also a semi symmetric non-metric connection.
-submanifold of a nearly trans-Sasakian manifold with a semi symmetric non-metric connection is also a semi symmetric non-metric connection.
Similarly, using (16), if  is
is  -vertical,
-vertical,  and
and  is parallel withrespect to
is parallel withrespect to , then the connection induced on a
, then the connection induced on a  -submanifold of a nearly trans-Sasakian manifold with a semi symmetric nonmetric connection is also a semi symmetric non-metric connection.
-submanifold of a nearly trans-Sasakian manifold with a semi symmetric nonmetric connection is also a semi symmetric non-metric connection.
Weingarten formula is given by
 (18)
(18)
for ,
, (resp.,
(resp., ) is the second fundamental form (resp., tensor) of
) is the second fundamental form (resp., tensor) of  in
in 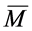 and
and  denotes the operator of the normal connection. Moreover, we have
denotes the operator of the normal connection. Moreover, we have
 (19)
(19)
4. Some Basic Lemmas
Lemma 4.1 Let  be a
be a  -submanifold of a nearly trans-Sasakian manifold
-submanifold of a nearly trans-Sasakian manifold 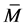 with a semi symmetric non-metric connection. Then
with a semi symmetric non-metric connection. Then
 (20)
(20)
 (21)
(21)
 (22)
(22)
for .
.
Proof. By direct covariant differentiation, we have

By virtue of (6), (9), (17) and (18), we get

Similarly, we have

On adding above equations, we have

Now using (6), (7) and equating horizontal, vertical and normal components in above equation, the lemma follows.
Lemma 4.2 Let  be a
be a  -submanifold of a nearly trans-Sasakian manifold
-submanifold of a nearly trans-Sasakian manifold 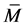 with a semi symmetric non-metric connection. Then
with a semi symmetric non-metric connection. Then
 (23)
(23)
for any .
.
Proof. By the use of (17), we have
 (24)
(24)
Also, we have
 (25)
(25)
From above equations, we get
 (26)
(26)
For a nearly trans-Sasakian manifold with a semi symmetric non-metric connection, we have
 (27)
(27)
Combining (26) and (27), the lemma follows.
In particular, we have the following corollary.
Corollary 4.3 Let  be a
be a  -vertical
-vertical  -submanifold of a nearly trans-Sasakian manifold
-submanifold of a nearly trans-Sasakian manifold  with a semi symmetric non-metric connection. Then
with a semi symmetric non-metric connection. Then
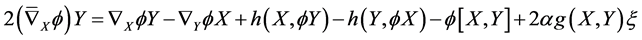 (28)
(28)
for any .
.
Similarly, by Weingarten formula, we can easily get the following lemma.
Lemma 4.4 Let  be a
be a  -submanifold of a nearly trans-Sasakian manifold
-submanifold of a nearly trans-Sasakian manifold  with a semi symmetric non-metric connection. Then
with a semi symmetric non-metric connection. Then
 (29)
(29)
for any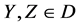 .
.
Corollary 4.5 Let  be a
be a  -horizontal
-horizontal 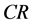 -submanifold of a nearly trans-Sasakian manifold
-submanifold of a nearly trans-Sasakian manifold  with a semi symmetric non-metric connection. Then
with a semi symmetric non-metric connection. Then
 (30)
(30)
for any .
.
Lemma 4.6 Let  be a CR-submanifold of a nearly trans-Sasakian manifold
be a CR-submanifold of a nearly trans-Sasakian manifold 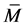 with a semi symmetric non-metric connection. Then
with a semi symmetric non-metric connection. Then
 (31)
(31)
for any .
.
Proof. As we have

Now, by using Gauss and Weingarten formulae in above equation, we have

Also, we have

From above equations, we get

In view of (10) and above equation, the lemma follows.
5. Parallel Distributions
Definition 5.1 The horizontal (resp., vertical) distribution  (resp.,
(resp., ) is said to be parallel [1] with respect to the semi symmetric non-metric connection
) is said to be parallel [1] with respect to the semi symmetric non-metric connection  on
on  if
if  (resp.,
(resp.,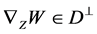 ) for any
) for any  (resp.,
(resp., ).
).
Now, we have the following proposition.
Proposition 5.2 Let  be a
be a  -vertical
-vertical  -submanifold of a nearly trans-Sasakian manifold
-submanifold of a nearly trans-Sasakian manifold  with a semi symmetric non-metric connection. Then
with a semi symmetric non-metric connection. Then
 (32)
(32)
for all .
.
Proof. By the parallelness of horizontal distribution , we have
, we have
 (33)
(33)
 , using the fact that
, using the fact that , (21) gives
, (21) gives
 (34)
(34)
Therefore in view of (7), we have
 (35)
(35)
From (22), we have
 (36)
(36)
for any .
.
Now, putting  and
and 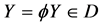 in (36), we get respectively
in (36), we get respectively
 (37)
(37)
 (38)
(38)
Hence from (37) and (38), we have
 (39)
(39)
Operating 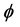 on both sides of (39) and using
on both sides of (39) and using , we get
, we get
 (40)
(40)
for all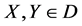 .
.
Now, for the distribution , we have the following proposition.
, we have the following proposition.
Proposition 5.3 Let  be a
be a  -vertical
-vertical  -submanifold of a nearly trans-Sasakian manifold
-submanifold of a nearly trans-Sasakian manifold  with a semi symmetric non-metric connection. If the distribution
with a semi symmetric non-metric connection. If the distribution  is parallel with a semi symmetric non-metric connection on
is parallel with a semi symmetric non-metric connection on . Then
. Then
 (41)
(41)
Proof. By using Weingarten formula, we have

and
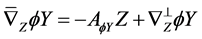
for . From above equations, we have
. From above equations, we have

Using (10) and (17), we obtain
 (42)
(42)
for any . Taking inner product with
. Taking inner product with  in (41), we get
in (41), we get
 (43)
(43)
If the distribution  is parallel, then
is parallel, then  and
and 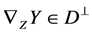 for any
for any . So from above equation, we get
. So from above equation, we get
 (44)
(44)
or
 (45)
(45)
which implies that .
.
Definition 5.4 A  -submanifold with a semi symmetric non-metric connection is said to be mixed totally geodesic if
-submanifold with a semi symmetric non-metric connection is said to be mixed totally geodesic if  for all
for all  and
and .
.
Definition 5.5 A normal vector field  with a semi symmetric non-metric connection is called
with a semi symmetric non-metric connection is called  -parallel normal section if
-parallel normal section if  for all
for all .
.
Now, we have the following proposition.
Proposition 5.6 Let  be a mixed totally geodesic
be a mixed totally geodesic 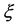 -vertical
-vertical  -submanifold of a nearly transSasakian manifold
-submanifold of a nearly transSasakian manifold 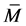 with a semi symmetric non-metric connection. Then the normal section
with a semi symmetric non-metric connection. Then the normal section  is
is  -parallel if and only if
-parallel if and only if  for all
for all .
.
6. Integrability Conditions of Distributions
In this section, we calculate the Nijenhuis tensor  on a nearly trans-Sasakian manifold
on a nearly trans-Sasakian manifold  with a semi symmetric non-metric connection. For this, first we prove the following lemma.
with a semi symmetric non-metric connection. For this, first we prove the following lemma.
Lemma 6.1 Let  be a nearly trans-Sasakian manifold with a semi symmetric non-metric connection. Then
be a nearly trans-Sasakian manifold with a semi symmetric non-metric connection. Then
 (46)
(46)
for any .
.
Proof. From the definition of nearly trans-Sasakian manifold with a semi symmetric non-metric connection , we have
, we have
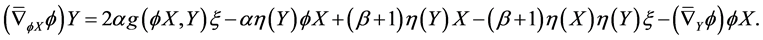 (47)
(47)
Also, we have
 (48)
(48)
Now, using (48) in (47), we get
 (49)
(49)
for any , which completes the proof of the lemma.
, which completes the proof of the lemma.
On a nearly trans-Sasakian manifold with a semi symmetric non-metric connection , Nijenhuis tensor is given by
, Nijenhuis tensor is given by
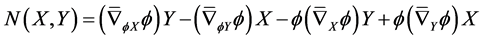 (50)
(50)
for any .
.
From (46) and (50), we get
 (51)
(51)
In view of (10), we have

Using above equation in (51), we obtain
 (52)
(52)
for any .
.
Proposition 6.2 Let  be a
be a  -vertical
-vertical  -submanifold of a nearly trans-Sasakian manifold
-submanifold of a nearly trans-Sasakian manifold  with a semi symmetric non-metric connection. Then the distribution
with a semi symmetric non-metric connection. Then the distribution  is integrable if the following conditions are satisfied:
is integrable if the following conditions are satisfied:
 (53)
(53)
for any .
.
Proof. The torsion tensor  of the almost contact metric structure
of the almost contact metric structure  is given by
is given by
 (54)
(54)
Thus, we have
 (55)
(55)
for any .
.
Suppose that the distribution  is integrable. So for
is integrable. So for ,
, . If
. If , then from (52) and (54), we have
, then from (52) and (54), we have
 (56)
(56)
for any  and
and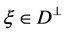 .
.
Replacing  by
by  for
for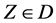 , we get
, we get
 (57)
(57)
Interchanging  and
and  for
for 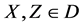 in (57), we have
in (57), we have
 (58)
(58)
Subtracting above equations, we get
 (59)
(59)
for any  and the assertion follows.
and the assertion follows.
Now, we prove the following proposition.
Proposition 6.3 Let  be a
be a  -submanifold of a nearly trans-Sasakian manifold
-submanifold of a nearly trans-Sasakian manifold  with a semi symmetric non-metric connection. Then
with a semi symmetric non-metric connection. Then
 (60)
(60)
for any .
.
Proof. For  and
and , we have
, we have
 (61)
(61)
The above equation is true for all , therefore transvecting the vector field
, therefore transvecting the vector field  both sides, we obtain
both sides, we obtain
 (62)
(62)
Interchanging the vector fields  and
and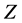 , we get
, we get
 (63)
(63)
From (62) and (63), we get
 (64)
(64)
for any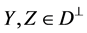 , which completes the proof.
, which completes the proof.
Proposition 6.4 Let  be a
be a  -submanifold of a nearly trans-Sasakian manifold
-submanifold of a nearly trans-Sasakian manifold  with a semi symmetric non-metric connection. Then the distribution
with a semi symmetric non-metric connection. Then the distribution 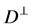 is integrable if and only if
is integrable if and only if
 (65)
(65)
for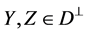 .
.
Proof. Proof of the theorem is similar as proof of the theorem 5.4 of [2] .
Corollary 6.5 Let  be a
be a 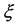 -horizontal
-horizontal  -submanifold of a nearly trans-Sasakian manifold
-submanifold of a nearly trans-Sasakian manifold  with a semi symmetric non-metric connection. Then the distribution
with a semi symmetric non-metric connection. Then the distribution 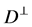 is integrable if and only if
is integrable if and only if
 (66)
(66)
for .
.