Harmonic Solutions of Duffing Equation with Singularity via Time Map ()
Keywords:Harmonic Solutions, Duffing Equation, Singularity, Time Map, Poincaré-Bohl Theorem
1. Introduction
We deal with the second-order Duffing equation
(1)
where 
is locally Lipschitzian and has singularity at the origin, 
is continuous and 
periodic. Our purpose is to establish existence result for harmonic solution of Equation (1). Arising from physical applications (see [1] for a discussion of the Brillouin electron beam focusing problem), the periodic solution for equations with singularity has been widely investigated, referring the readers to [2] -[6] and their extensive references.
As is well known, time map is the right tool to build an approach to the study of periodic solution of Equation (1) (see [7] -[9] ). However, the work mainly focused on the equations without singularity. Our goal in this paper is to study the periodic solution of Equation (1) with singularity via time map. There is a little difference between our time map and the time map in [7] [9] . We now introduce the time map.
Consider the auxiliary autonomous system
(2)
and suppose that
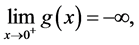
Obviously, the orbits of system (2) are curves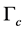 
determined by the equation
where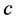 
is an arbitrary constant.
In view of the assumptions (g0), (g1) and (G0), there exists a
, such that for
, 
is a closed curve. Let 
be a solution of (2) whose orbit is
. Then this solution is periodic, denoting by 
the least positive period of this solution. It is easy to see that
(3)
where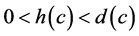
, 
, 
,
.
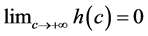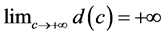We recall an interesting result in [7] . Ding and Zanolin [7] proved that Equation (1) without singularity possesses at least one T-periodic solution provided that
and a kind of nonresonance condition for the time map
(4)
where
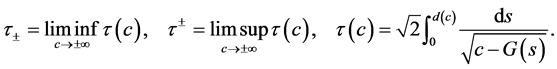
Now naturally, we consider the question whether Equation (1) has harmonic solution when we permit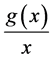 
cross resonance points and use a kind of nonresonance condition for time map. In the following we will give a positive answer. In order to state the main result of this paper, set
(5)
and assume that
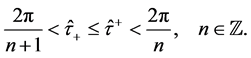
Our main result is following.
Theorem 1.1 Assume that
, 
and 
hold, then Equation (1) has at least one 2π- periodic solution.
In this case, we generalize the result in [7] to Equations (1) with singularity.
The remainer of the paper is organized as follows. In Section 2, we introduce some technical tools and present all the auxiliary results. In Section 3, we will give the proof of Theorem 1.1 by applying the phase-plane analysis methods and Poincaré-Bohl fixed point theorem.
2. Some Lemmas
we assume throughout the paper that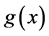 
is locally Lipschitz continuous. In order to apply the phase-plane analysis methods conveniently, we study the equation
(6)
where 
is continuous and has a singularity at
. In fact, we can take a parallel translation 
to achieve the aim. Then the conditions 
and 
become
Dropping the hats for simplification of notations, we assume that
and
Thus,
(7)
and 
and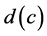 
in (3) satisfy
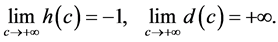
We will prove Theorem 1.1 under conditions
, 
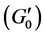
and 
instead of conditions
, 
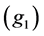and
.
Consider the equivalent system of (6):
(8)
Let 
be the solution of (8) satisfying the initial condition
We now follow a method which was used by [4] [6] and shall need the following result.
Lemma 2.1 Assume that conditions 
and 
hold. They every solution of system (8) exists uniquely on the whole t-axis.
By Lemma 2.1, we can define Poincaré map 
as follows
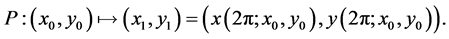
It is obvious that the fixed points of the Poincaré map 
correspond to 
-periodic solutions of system (8). We will try to find a fixed point of
. To this end, we introduce a function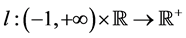
,
Lemma 2.2 Assume that 
and 
hold. Then, for any
, there exists 
sufficiently large that, for
,
where 
is the solution of system (8) through the initial point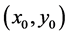
.
This result has been proved in [6] and we omit it.
Using Lemma 2.2, we see that 
for 
if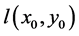 
is large enough. Therefore, transforming to polar coordinates
, 
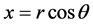, system (8) becomes
(9)
Denote by 
the solution of (9) with
Thus, we can rewrite the Poincaré map in the form
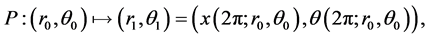
where
.
For the convenience, two lemmas in [6] will be written and the proof can be found in [6] .
Lemma 2.3 Assume that 
and 
hold. Then there exists a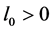 
such that, for
,
.
Lemma 2.4 Assume that
, 
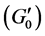and 
hold. Then there exists a 
such that, for
,
is a star-shaped closed curve about the origin
.
Lemma 2.5 Assume that
, 
and 
hold. Denote by 
the time for the solution 
to make one turn around the origin. Then 
as
, where 
and 
are given in (7).
Proof. Without loss of generality, we may assume that
. From Lemma 2.3, we have 
for sufficiently large 
and
. Hence, there exist 
such that
, and
Throughout the lemma, we always assume that 
is large enough.
(1) We shall first estimate 
and
. We can refer to Lemma 2.6 in [6] and obtain
, 
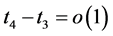as
.
(2) We now estimate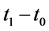 
and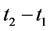
. According to conditions 
and
, we can choose a constant 
such that 
for
. Set
(10)
Then,
Therefore, for
,
Note that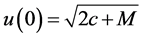
, we get
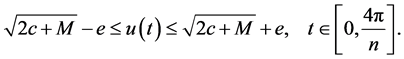
Since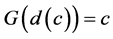
, we have
where
. By condition
, we know that 
increases for x sufficiently large, and tends to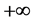 
as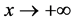
. Therefore, there exist constants 
such that
(11)
By (10) and (11), we have
(12)
Let 
be such that
, and
. Following (12), we derive
(13)
that is,
Consequently,
Integrating both sides of the above inequality from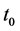 
to
, we obtain
(14)
Recalling the conditions 
and (11), we know that there is
, such that
. Applying Lemma 2.8 in [6] , we can derive
(15)
for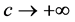
. Combining (14) and (15), we have
From [10] , we know that
for
. Hence,
In the following, we deal with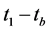
. Integrating 
from 
to
, we get
(16)
By (13), we derive
(17)
On the other hand, from (11) we have
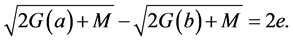
As a result,
Accordingly,
(18)
Meanwhile, following
, for any given 
sufficiently large, there exist 
large enough, such that
(19)
Combining (16)-(19), we get
for
, where
. Thus,
(20)
Using the same arguments as above, we can get
(21)
By the conditions (20), (21), we have
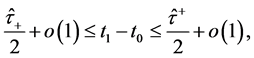
Recalling
, 
, we have
The proof is complete.
3. Proof of Theorem 1.1
In this section, we establish the existence of harmonic solutions for Equation (1) by appealing to Poincaré-Bohl theorem [11] . We consider the Poincaré map
From Lemma 2.5 and condition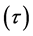
, we obtain
which implies
Thus, the image 
cannot lie on the line
. Therefore, the Poincaré-Bohl theorem guarantees that the map 
has at least one fixed point, i.e. Equation (6) has at least one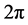 
-periodic solution.