Wavelet Interpolation Method for Solving Singular Integral Equations ()
1. Introduction
In the early 1900s, Ivar Fredholm solved the integral equations named after him,
where the function 
and continuous kernel 
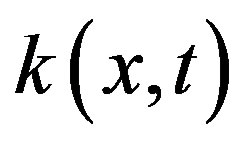are given, and the unknown function y(x) is to be determined. A numerical method of solving this equation has been shown in [1]. In this study, we discuss the numerical solution of singular Fredholm integral equation of the second kind which is defined as follows:
(1)
where the functions 
and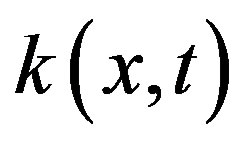 
are given, the numerical solution for Equation (1) is to provide an approximation for the unknown function
. In fact, Equation (1) is known as an Abel’s integral equation which is defined by Niels Henrik Abel. There are many approaches to find a numerical solution of the Abel’s equation [2], such as Gauss-Jacobi quadrature rule which was proposed by Fettis (1964), orthogonal polynomials expansion by Kosarev (1973), the Chebyshev polynomials of the first kind by Piessens and Verbaeten (1973) and Piessens (2000), etc. Recently, K. Maleknejad, M. Nosrati and E. Najafi solved the equation by using wavelet Galerkin method [3]. Here we used Coiflets to find a numerical solution of Equation (1).
The Coiflets are discussed in the next section briefly. In Section 3, we solve Abel’s Equation (1) by using Coiflets. The error analysis is discussed in Section 4. Finally, we apply our method for two singular equations in the examples and compare our method with other method [3]. We obtain numerical solutions which have achieved better accuracy.
2. Coiflets and Wavelet Interpolation
In the context of wavelet theory, we usually deal with wavelets and scaling functions [4]. The wavelet function is defined by building a sequence upon scaling functions generated by
. Choosing some suitable sequence, 
, we obtain the following dilation equation,
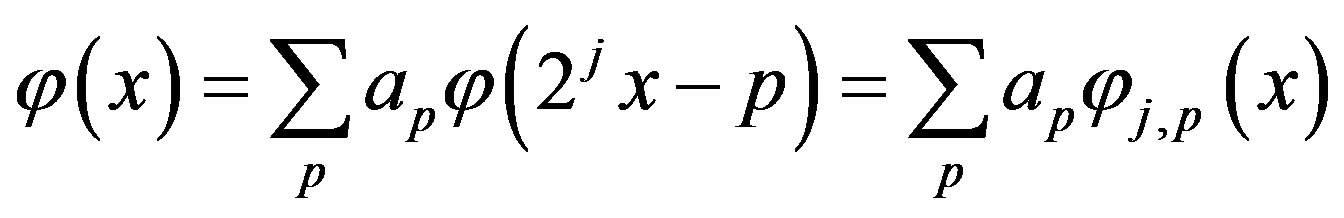
A nested of subspaces 
of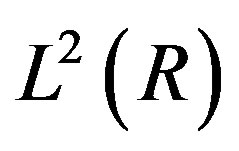 
is defined such that,
which means that for any function 
it can be expressed as:
If the basis functions of a subspace are orthogonal at the same level, then a given function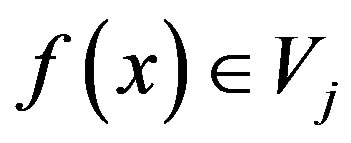 
can be expressed as follows:
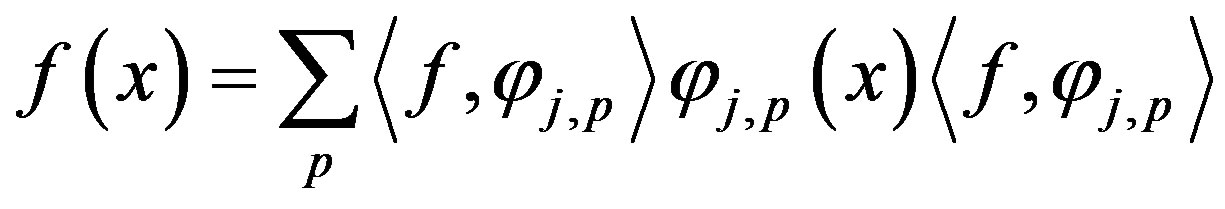
where
If the nested sequence of the subspaces 
has the following properties then it is called a multiresolution analysis (MRA):
1) 
2) 
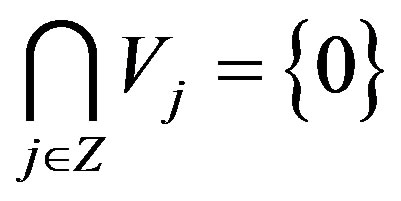
3) 
4) 
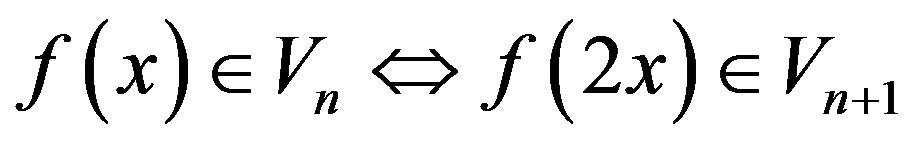
5) there exists a function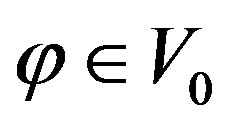 
such that 
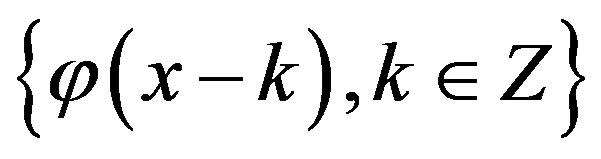is an orthogonal basis for
.
The wavelet function is constructed in the orthogonal complement of each subspace 
in 
which is denoted by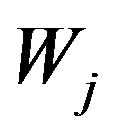
. This means
. Since
we have 
and
. The set 
forms a basis for
, and can be obtained from the following equation:
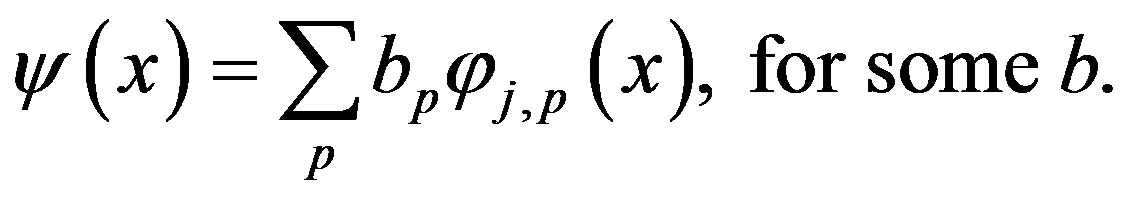
The orthogonally of 
on 
means that any member of 
is orthogonal to the members of
, that is,
In fact, scaling function and wavelet have the following properties:
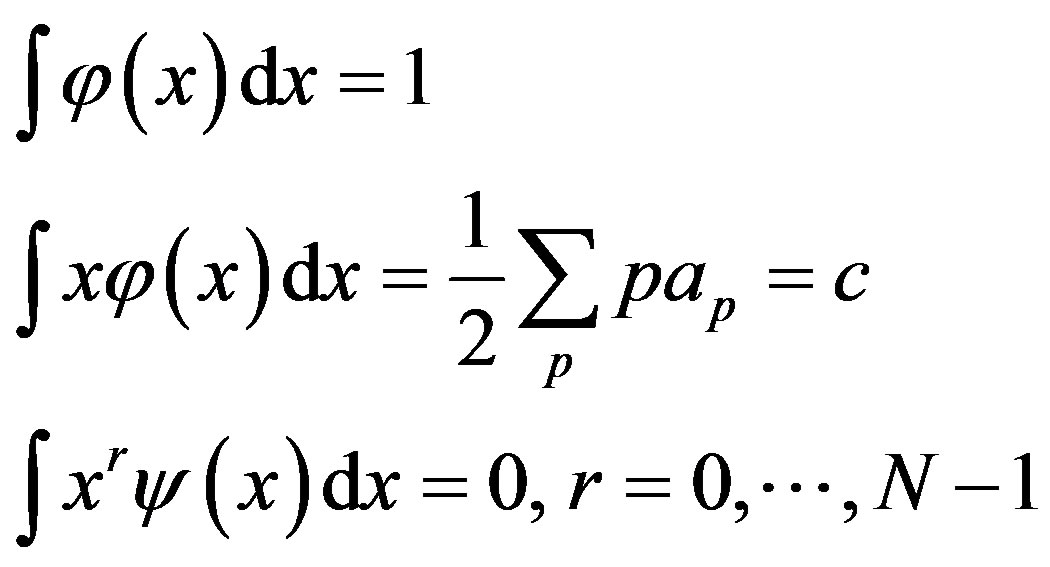
where 
is the compact support of 
and 
In what follows, we will recall a scaling function interpolation theorem and the definition of Coiflets. As an application, we will use Coiflets and this interpolation formula to find numerical solutions of singular integral equations.
Definition 2.1. The Coifman wavelet system (Coiflet) of order L is an orthogonal multiresolution wavelet system with
Lin and Zhou proved the following interpolation theorem in R2 and
:
Theorem 2.1. [5] Assume the function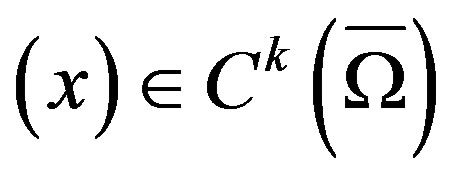
, where 
is a bounded open set in
, 
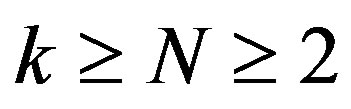Let, for
,
where the index
and sup denotes the support of the function.
In addition the moments 
satisfy
Then
(2)
where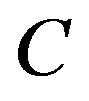 
is a constant depending only on 
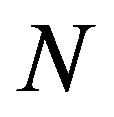and diameter of
;
3. Solving Singular Fredholm Integral Equation Using Coiflets
This section provides a method of finding numerical solution of Equation (1). In what follows, we assume that 
and 
satisfies Lipschitz condition. The unknown function 
in Equation (1) can be expressed in term of scaling functions in the subspacev, where the function 
is approximated by 
such that;
(3)
To find the numerical solution we need to determinate the unknowns 
in Equation (3).
By substituting Equation (3) in (1) we have the following equation,
which is equivalent to the equation,
(4)
By providing sufficient collocation points in 
for Equation (4) we will have a linear system of linear equations with unknown
. In fact, the linear system can be written as the following matrix equation,
where
,
and
is obtained from the left hand side of Equation (4). Subsequently, we substitute the solutions of ap into Equation (3), and obtain an approximate solution of the integral equation.
4. Error Analysis
The integral Equation (1) can be rewritten as follows [3].
(5)
where
Then the integral Equation (1) is equivalent to the following equation,
(6)
The next theorem shows the convergence rate of our method for solving Equation (1). Without loss of generality, we suppose that the integral equation is defined on the interval
.
Theorem 4.1. In Equation (1), suppose that the function k satisfies the Lipchitz condition. Moreover, 
is continuous on the interval
. For
,
(7)
is an approximate solution of the unknown function in Equation (1) with coefficients obtained in Section 3. Then
for some constant c.
Proof: We prove in two cases, one at singularities (case 1) and the other at the points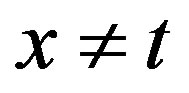 
(case 2).
Case 1. In Equation (1) when
, the function 
satisfies the Lipchitz condition and the function 
is continuous, then Equation (1) is equivalent to Equation (6), then the function 
which gives us the exact solution.
Case 2. In this case we don’t have singularities, and Equation (1) is equivalent to Equation (6) and 
. Subtracting Equation (7) from (6) and applying the norm, we have
(8)
The unknown function 
can be interpolated using Coiflet such that
(9)
If we add and subtract Equation (9) to (8), then Equation (8) becomes:
(10)
Notice that 
is finite, then let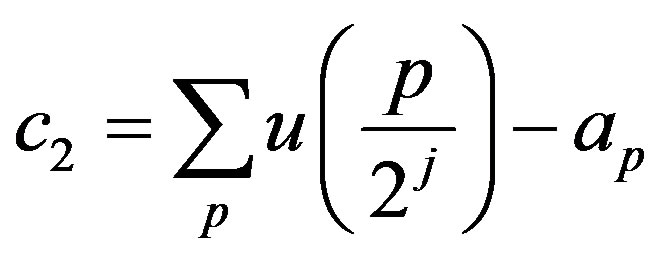 
and by using Equation (2),
Equation (10) becomes
for some constant c which is absorbed from the above inequality.
5. Numerical Examples
In the following examples we are solving singular Fredholm integral equation of the second kind by using Coiflet of order 5 and calculate errors between the exact and numerical solutions at level j = −10. The errors are shown in Table 1.
Example 1.
We solve the singular integral equation
Table 1. The absolute error for Examples 1 and 2.
with
and the exact solution is
.
Example 2.
We consider the following singular integral equation
with the exact solution
.
6. Conclusion
We apply our method to the same examples shown in [3]. Table 1 indicates that our solutions have better accuracy than the solutions obtained in [3]. Our method is robust and efficient. There are other questions such as finding solutions at different levels of subspaces and solving nonlinear integral equations which will be our next research projects.