Cosmology Should Directly Use the Doppler’s Formula to Calculate the Red Shift of Ia Supernova
—The Proofs That Metric Red Shift Is Inapplicable and Dark Energy Does Not Exist ()
1. Introduction
As we known that there are mainly three mechanisms leading to the red shift of spectrum. The first is gravity which relates to mass and gravity constant. The second is Doppler’s effect which relates to velocity. The third is the Compton scattering which is related to the energy transformation of photon. According to the Hubble law, the spectrum red shift of extragalactic nebula was proportional to the distance between observer and luminous celestial body. The red shift of cosmology is considered to be the Doppler’s effect. In 1998, cosmic observers found that the red shift of Ia supernova deviated from the linear relation of the Hubble law. By fitting the observation values with standard theory of cosmology, cosmologists declared that about 26% material in the universe was dark material and about 70% was dark energy. The universe seems to do accelerating expansion [1,2].
The red shift of cosmology is considered to be caused by the receding motions of celestial bodies, so its essence is the Doppler’s effect related to speed. We should use Doppler’s formula to calculate the red shift. However, it is strange that the basic formula used to calculate the relation of red shift and distance of Ia supernova is completely different from the Doppler formula. The basic formula used in cosmology is [3]
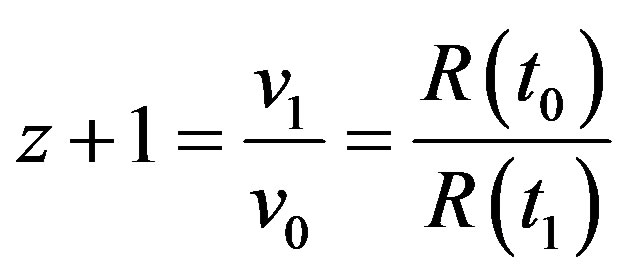 (1)
(1)
The formula is based on the R-W metric in which  is the frequency of emitted light at time
is the frequency of emitted light at time ,
,  is the frequency of received light at time
is the frequency of received light at time . The formula is related to scalar factor
. The formula is related to scalar factor . But the Doppler’s formula is related to speed factor
. But the Doppler’s formula is related to speed factor . It is proved in this paper that they can not be consistent. This inconsistence is not allowed in physics.
. It is proved in this paper that they can not be consistent. This inconsistence is not allowed in physics.
It is proved strictly that Formula (1) is only the result of first order approximation. When higher order approximations are taken into account, the restriction condition  will be obtained. Therefore, Formula (1) is only suitable to describe the process of spatial uniform expansion; it’s unsuitable for the practical process of the universal expansion with acceleration. More strictly, if we do not consider approximation, both Formula (1) and the restriction relations do not exist. That is to say, we have no metric red shift actually.
will be obtained. Therefore, Formula (1) is only suitable to describe the process of spatial uniform expansion; it’s unsuitable for the practical process of the universal expansion with acceleration. More strictly, if we do not consider approximation, both Formula (1) and the restriction relations do not exist. That is to say, we have no metric red shift actually.
In fact, the W-R metric is only a mathematical structure of space-time, rather than an independent law of physics. It is introduced to simplify the Einstein’s equation of gravity field to obtain the Friedmann equation of cosmology. It is not absolutely necessary to use the R-W metric in cosmology. Using normal coordinates directly, we can also establish the equation of cosmology based on the Einstein’s equation of gravity field. In this case, there is no the metric red shift formula (1). In this sense, the red shift of metric is not independent in physics. If it is correct, it cannot be contradicted with the Doppler’s and gravity red shifts.
The further analysis indicates that the R-W metric violates the invariability principle of light’s speed in vacuum when it is used to describe the uniform motion of light’s source. The time contraction between observer and moving light’s source is also neglected when the R-W metric is use to describe the spatial expansion. So the R-W metric is not one of special relativity and is unsuitable to be used as the basic space-time frame in cosmology. Especially, it is not suitable to be used to describe the high red shift of supernova in which the high speed expansion of the universe is involved.
In summary, the formula used to calculate the relation of red shift and distance of Ia supernova in cosmology has essential mistake. Therefore, dark energy and the accelerating universe are incredible. The Doppler formula should be used directly to calculate red shift of Cosmology. It is proved by the method of numerical calculation that if the Doppler’s formula and the (revised) Newtonian formula of gravity are used, the high red shift of Ia supernova can be explained well. We do not need the hypothesis of dark energy and accelerating universe again.
Let’s discuss the problem in the metric red shift formula. The inconsistence between the metric red shift and the Doppler’s red shift will be discussed in appendix.
2. Unavailability of Metric Red Shift Formula
2.1. The Restriction Condition  for the Metric Red Shift Formula
for the Metric Red Shift Formula
Standard cosmology uses the R-W metric to describe the universal space-time with form
 (2)
(2)
Here  is scalar factor and
is scalar factor and  is considered as the factor of spatial curvature. The co-moving coordinate is used in cosmology. The space is considered flat when
is considered as the factor of spatial curvature. The co-moving coordinate is used in cosmology. The space is considered flat when . When (2) is used to describe the expansive universe, luminous celestial bodies are considered to be fixed on the coordinate
. When (2) is used to describe the expansive universe, luminous celestial bodies are considered to be fixed on the coordinate  which do not changed with time. Let’s repeat the process to obtain Formula (1) based on the R-W metric. Suppose that light moves along the radius direction
which do not changed with time. Let’s repeat the process to obtain Formula (1) based on the R-W metric. Suppose that light moves along the radius direction  with
with , we get from (2)
, we get from (2)
 (3)
(3)
Light source is fixed at point 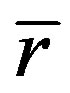 and
and  does not change with time. But to light’s motion,
does not change with time. But to light’s motion,  changes with time. Suppose that photon’s coordinate is
changes with time. Suppose that photon’s coordinate is  at moment
at moment  and photon arrives at the original point
and photon arrives at the original point  at moment
at moment . The integral of (3) is [3]
. The integral of (3) is [3]
 (4)
(4)
The negative sign indicates that light moves along the direction to decrease . Suppose that a light wave is emitted during the period of time from
. Suppose that a light wave is emitted during the period of time from  to
to  with period
with period . Observer receives the light during the period of time from
. Observer receives the light during the period of time from  to
to  with period
with period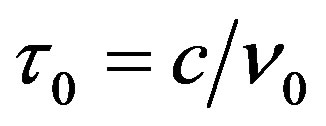 . According to the current understanding, because
. According to the current understanding, because  and
and  are decided by the same
are decided by the same , we have
, we have
 (5)
(5)
Because 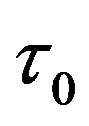 and
and  are small, according to present theory, we obtain from (5)
are small, according to present theory, we obtain from (5)
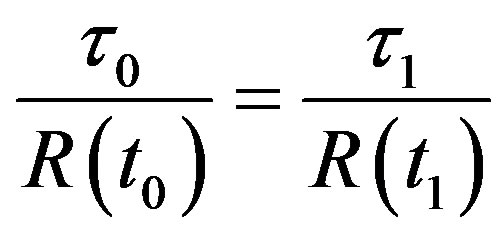 (6)
(6)
Based on (6) and the definition of red shift, we obtain (1). By considering (1) and the Friedmann equation of cosmology, as described in Section 3, we can obtain (1). We now prove that (6) is the result of the first order approximation. If higher order approximations are considered, we can obtain  or
or  constant. So the formula (1) is only suitable to the uniformly expansive universe, unsuitable to describe the universal process with acceleration. Let
constant. So the formula (1) is only suitable to the uniformly expansive universe, unsuitable to describe the universal process with acceleration. Let
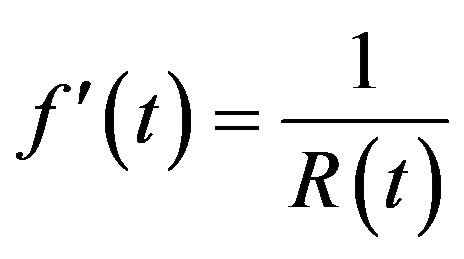 (7)
(7)
and take the integral of (5), we have
 (8)
(8)
By developing (8) into the Taylor series, we obtain
 (9)
(9)
Because  and
and  are very small, if let the items with same orders are equal to each other, we have
are very small, if let the items with same orders are equal to each other, we have
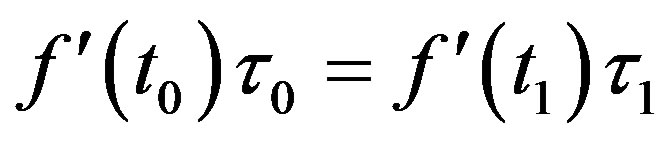 (10)
(10)
 (11)
(11)
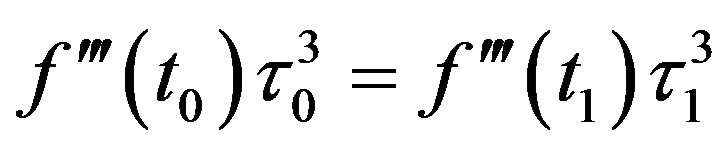 (12)
(12)
 (13)
(13)
By considering (7), (10) is just (6). So the metric red shift formula (1) is actually the approximation of first order. (11) can be written as
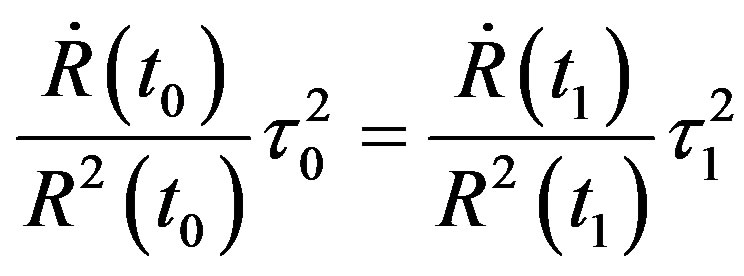 (14)
(14)
Substituting (6) in (14), we obtain
 (15)
(15)
Because  and
and  are arbitrary, (15) indicates that
are arbitrary, (15) indicates that , i.e., the expansion speed does not depend on time and we have
, i.e., the expansion speed does not depend on time and we have . From (12), we have
. From (12), we have
 (16)
(16)
Substituting (6) and (15) in (16), we get
 (17)
(17)
It is still (6). From (13), we get
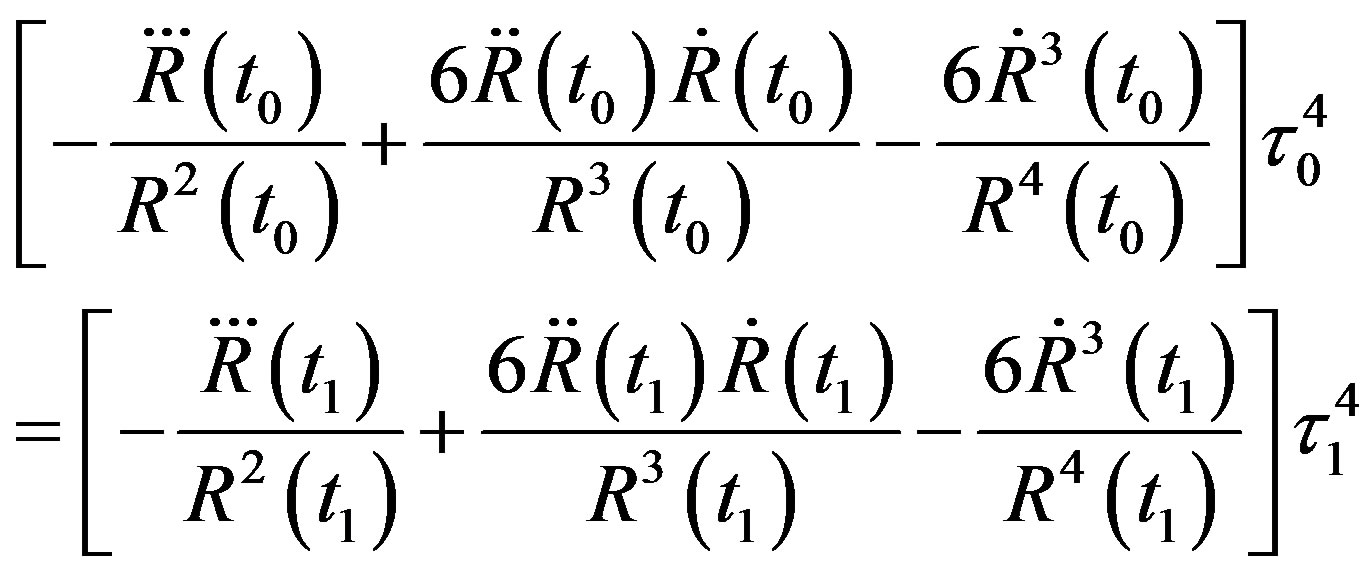 (18)
(18)
Because of , we have
, we have . By considering (15), we still obtain (6). It can be known that no matter what high orders are considered, we always obtain these two relations. So the metric can only be written as
. By considering (15), we still obtain (6). It can be known that no matter what high orders are considered, we always obtain these two relations. So the metric can only be written as
 (19)
(19)
That is to say, if (6) holds, it can only be used to describe the uniform expansion of space. Because gravity exists in the universe, Formula (1) can not be used to describe the practical process of the universal expansion with acceleration.
More strictly, we only have Formula (9). Formulas (10)- (13) do not exist in mathematics actually. It means that it is impossible for us to have a new red shift mechanism based on the R-W metric, which is different from the Doppler’s and gravity red shifts. The reason is that the R-W metric is only a mathematical structure of spacetime, rather an independent physical law.
3.2. The Problem of the R-W Metric
Firstly, constant  in (2) is considered as curvature factor and the metric is considered to describe flat spacetime when
in (2) is considered as curvature factor and the metric is considered to describe flat spacetime when . This idea has been proved wrong that when scalar factor
. This idea has been proved wrong that when scalar factor  is related to time [4]. That is to say that the R-W metric has no constant curvature in general situations. By using the formula of the Riemannian geometry and making strict calculation, the spacetime curvatures of the R-W metric actually are
is related to time [4]. That is to say that the R-W metric has no constant curvature in general situations. By using the formula of the Riemannian geometry and making strict calculation, the spacetime curvatures of the R-W metric actually are
 (20)
(20)
Here  is the curvature of space-time closing part and
is the curvature of space-time closing part and  is the curvature of pure spatial part. This result is completely different from the current understanding. Therefore, constant
is the curvature of pure spatial part. This result is completely different from the current understanding. Therefore, constant  is not the factor of spatial curvature. Instead, it is a certain adjustable parameter. The R-W metric does not represent the flat space-time when
is not the factor of spatial curvature. Instead, it is a certain adjustable parameter. The R-W metric does not represent the flat space-time when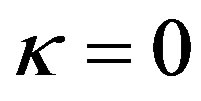 .
.
In fact, we can use more simple method to prove the result above. As we know in geometry, the principle to judge an arbitrary metric to be flat or not is that if we can find a coordinate to transform the metric to one with flat space-time, the original metric is flat essentially. If we cannot, the original metric is curved in essence. By using common coordinate system, the four dimensional metric of flat space-time is
 (21)
(21)
By using the co-moving coordinate or the coordinate transformation 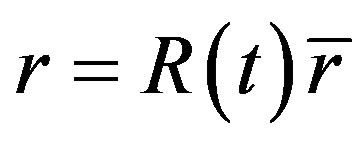 in (21), we obtain
in (21), we obtain
 (22)
(22)
However, let  in (2), we obtain
in (2), we obtain
 (23)
(23)
(22) is different from (23) unless . Because we can obtain (21) by using
. Because we can obtain (21) by using  in (22), so the space-time described by (22) is flat in essential. However, it is easy to see that when
in (22), so the space-time described by (22) is flat in essential. However, it is easy to see that when  we can not find a coordinate transform to change (23) into (21), so (23) can not be the metric of flat space-time.
we can not find a coordinate transform to change (23) into (21), so (23) can not be the metric of flat space-time.
We can prove generally that if (23) described light’s motion in flat space, it would violate the invariability principle of light’s speed in vacuum. For the light source fixed on the reference fame, its coordinate 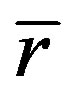 does not change with time. But for the motion of light, the coordinate
does not change with time. But for the motion of light, the coordinate  changes with time. Suppose that light moves along the direction of radius, we have
changes with time. Suppose that light moves along the direction of radius, we have  and
and . According to (23), we have
. According to (23), we have
 (24)
(24)
The velocity of light relative to the observer rested at the original point of coordinate system is
 (25)
(25)
(25) indicates that light’s velocity is related to the velocity of special expansion. Suppose that space expands uniformly, let , according to (25), we have
, according to (25), we have . At the moment when light is emitted out, (25) is just the Galileo’s addition rule of light’s velocity. When light moves towards observer, minus sign is taken and light’s speed is less than its speed in vacuum. When the light moves apart from observer, plus sign is taken and light’s speed is great than its speed in vacuum. Especially, because
. At the moment when light is emitted out, (25) is just the Galileo’s addition rule of light’s velocity. When light moves towards observer, minus sign is taken and light’s speed is less than its speed in vacuum. When the light moves apart from observer, plus sign is taken and light’s speed is great than its speed in vacuum. Especially, because  increases with time, enough long time later, light’s speed may greatly exceed its speed in vacuum. This is not allowed in physics, so the R-W metric is not the metric of special relativity.
increases with time, enough long time later, light’s speed may greatly exceed its speed in vacuum. This is not allowed in physics, so the R-W metric is not the metric of special relativity.
We can use two simple examples to show that if (23) describe the metric of flat space, it can not describe light’s motion. Suppose that light’s source is located at point  and emits a bundle of light at time
and emits a bundle of light at time . This light arrives at observer located at position
. This light arrives at observer located at position  at time
at time . Suppose that space expands in a uniform speed which corresponds to the uniform motion of light’s source. Let
. Suppose that space expands in a uniform speed which corresponds to the uniform motion of light’s source. Let  and take the integral of (24), we obtain
and take the integral of (24), we obtain
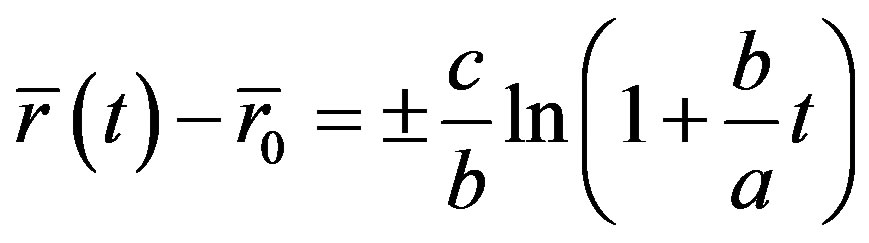 (26)
(26)
Let ,
,  and
and , we get the speed of light’s source
, we get the speed of light’s source 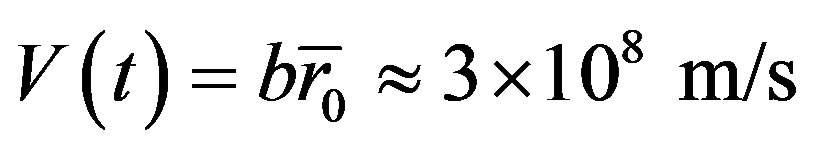 which is near light’s speed. Suppose that observer is at the original point of coordinate system with
which is near light’s speed. Suppose that observer is at the original point of coordinate system with , according to (26), we have
, according to (26), we have  and
and . This result is obviously incorrect. According to special relativity, light’s speed does not depend on the speed of light’s source. Because the initial distance between observer and light’s source is 1m, the time that light arrives at observer should be
. This result is obviously incorrect. According to special relativity, light’s speed does not depend on the speed of light’s source. Because the initial distance between observer and light’s source is 1m, the time that light arrives at observer should be . The error is as great as 58%. In fact, charged particles move at near light’s speed in high energy accelerators. And experiments show that radiation lights can not propagate in this way.
. The error is as great as 58%. In fact, charged particles move at near light’s speed in high energy accelerators. And experiments show that radiation lights can not propagate in this way.
Suppose that the acceleration of spatial expansion is a constant and let . Take
. Take 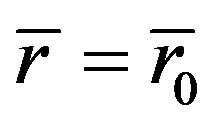 when
when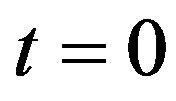 . The integral of (24) is
. The integral of (24) is
 (27)
(27)
Taking ,
,  and
and , we have
, we have  and
and . If
. If , we have
, we have . The speed of light’s source is
. The speed of light’s source is
 . Meanwhile, we have
. Meanwhile, we have
 and
and .
.
The first item in (27) becomes minus infinite and the second item is meaningless, so (27) can not yet describe the motion of light in this case. Therefore, in general, the R-W metric is unsuitable to describe light’s motion.
This problem does not exist in (22). Suppose that light moves along the direction of radius, we have
 (28)
(28)
 (29)
(29)
By considering (29), light’s velocity is
 (30)
(30)
It indicates that light’s speed is unchanged in vacuum, so (22) is the metric of special relativity.
We have  in (23), so it is considered to have a uniform time for whole space. However, because of spatial expansion, the clock fixed at position
in (23), so it is considered to have a uniform time for whole space. However, because of spatial expansion, the clock fixed at position 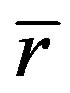 has a speed relative to observer who is rested at the original point of coordinate system. According to special relativity, there is time delay between them, but (23) can not describe this relation. According to (22), we have
has a speed relative to observer who is rested at the original point of coordinate system. According to special relativity, there is time delay between them, but (23) can not describe this relation. According to (22), we have
 (31)
(31)
This is just the delay of special relativity, so (22) is the metric of relativity in flat space-time, but (23) is not. Similarly, it is proved in mathematics that the four dimensional metric in which three dimensional space has constant curvature  is
is
 (32)
(32)
By using co-moving coordinate in (32), we obtain
 (33)
(33)
When , (33) becomes (22), so (33) is correct metric which satisfies special relativity with special curvature
, (33) becomes (22), so (33) is correct metric which satisfies special relativity with special curvature . We have
. We have ,
,  and
and 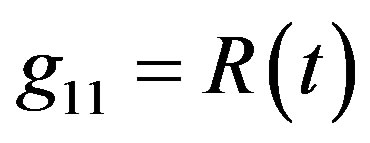 in (33). Its form is much more complicated than the R-W metric (2). When light moves along the direction of radius with
in (33). Its form is much more complicated than the R-W metric (2). When light moves along the direction of radius with , we have
, we have
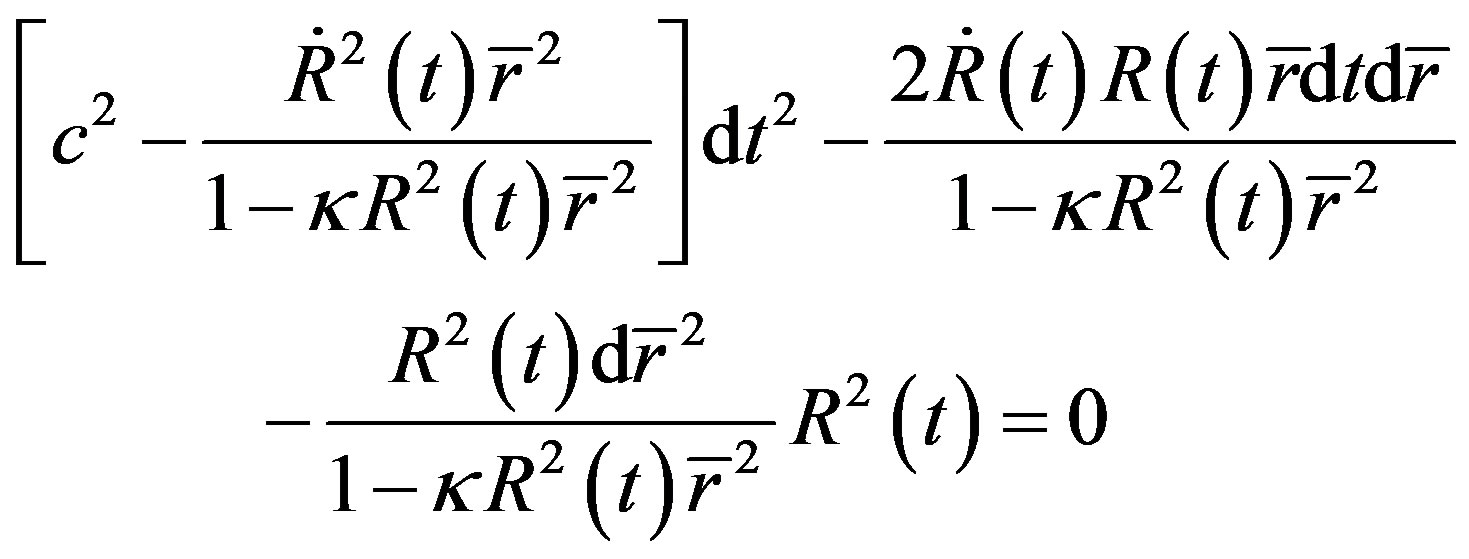 (34)
(34)
We obtain
 (35)
(35)
If we use (29) and (35) to calculate the red shift of cosmology, i.e., also so called metric red shift, the results are certainly related to velocity. However, we can not separate variables in (29) and (35), so we can not write them in the simple form of (3) and can not get the same formulas similar to (1).
The R-W metric violates the invariability principle of light’s speed in vacuum and neglects the time delay between observers and moving light’s source caused by relative motion. So the red shift formula of metric based on the R-W metric can not be correct. It is improper to use the metric as the basic frame of space-time in cosmology. We should use the Doppler’s formula to calculate the red shift directly.
2.3. Other Problems in the Formula for Calculating the Red Shift of Ia Supernova
Based on (1) in cosmology, the following formula is obtained to calculate the relation of red shift and distance of Ia supernova [5]
 (36)
(36)
Here 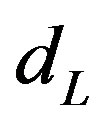 is luminosity distance. In light of the R-W metric, we have
is luminosity distance. In light of the R-W metric, we have . By fitting with practical observations, cosmologists deduced that dark energy was about 70% and non-baryon dark material was about 26% of the universal material. An accelerating universe is assumed.
. By fitting with practical observations, cosmologists deduced that dark energy was about 70% and non-baryon dark material was about 26% of the universal material. An accelerating universe is assumed.
We now discuss the problems existing in (36). The Friedmann equation of cosmology is
 (37)
(37)
Here  is the density of normal material,
is the density of normal material, 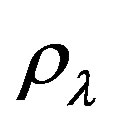 is the density corresponding to cosmic constant. At present time
is the density corresponding to cosmic constant. At present time , we have
, we have  and
and , the Friedmann equation of cosmology can be written as
, the Friedmann equation of cosmology can be written as
 (38)
(38)
Defining critical density  as
as
 (39)
(39)
Let ,
,  ,
,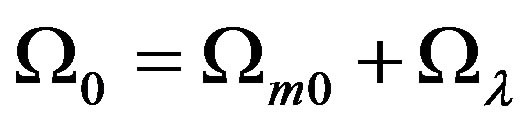 , we write (38) as
, we write (38) as
 (40)
(40)
Let , we have
, we have  at present time. Because
at present time. Because  is a constant, we can write the Friedmann equation as
is a constant, we can write the Friedmann equation as
 (41)
(41)
By considering
 or
or  (42)
(42)
(41) can be written as
 (43)
(43)
We have 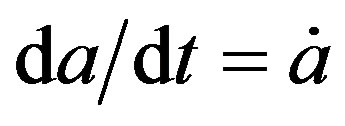 or
or , so (4) can be written as
, so (4) can be written as
 (44)
(44)
The upper limit of the integral is  and lower limit is
and lower limit is . By intruding so-called energy effective curvature density [5]
. By intruding so-called energy effective curvature density [5]
 (45)
(45)
We have 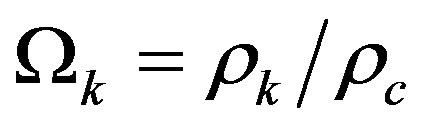 and
and . We write (40) as
. We write (40) as
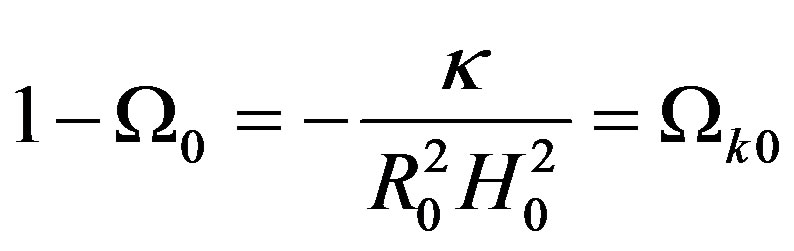 (46)
(46)
According to Document [5], (46) is written as
 (47)
(47)
By introducing transformation  in (44) we obtained (36). However, (47) is obviously wrong. (46) contains constant
in (44) we obtained (36). However, (47) is obviously wrong. (46) contains constant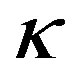 , but (47) does not. According to (46), when
, but (47) does not. According to (46), when  we have
we have , so
, so  is limited. But according to (47), when
is limited. But according to (47), when  we have
we have . It means that
. It means that  is infinite at present time in flat space. But this is completely impossible. According to (46), correct result should be
is infinite at present time in flat space. But this is completely impossible. According to (46), correct result should be
 (48)
(48)
In fact, it is unnecessary for us to introduce relation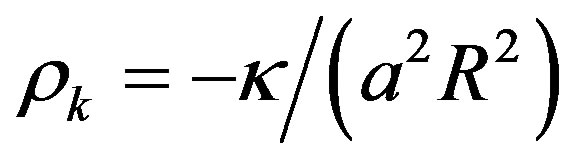 . Whether or not space is flat depends on
. Whether or not space is flat depends on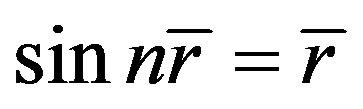 ,
,  or
or . For flat space, by taking
. For flat space, by taking  in (41) and substituting it in (44), and by considering
in (41) and substituting it in (44), and by considering  and
and , we get
, we get
 (49)
(49)
Because (47) can not hold, (36) can only be written as
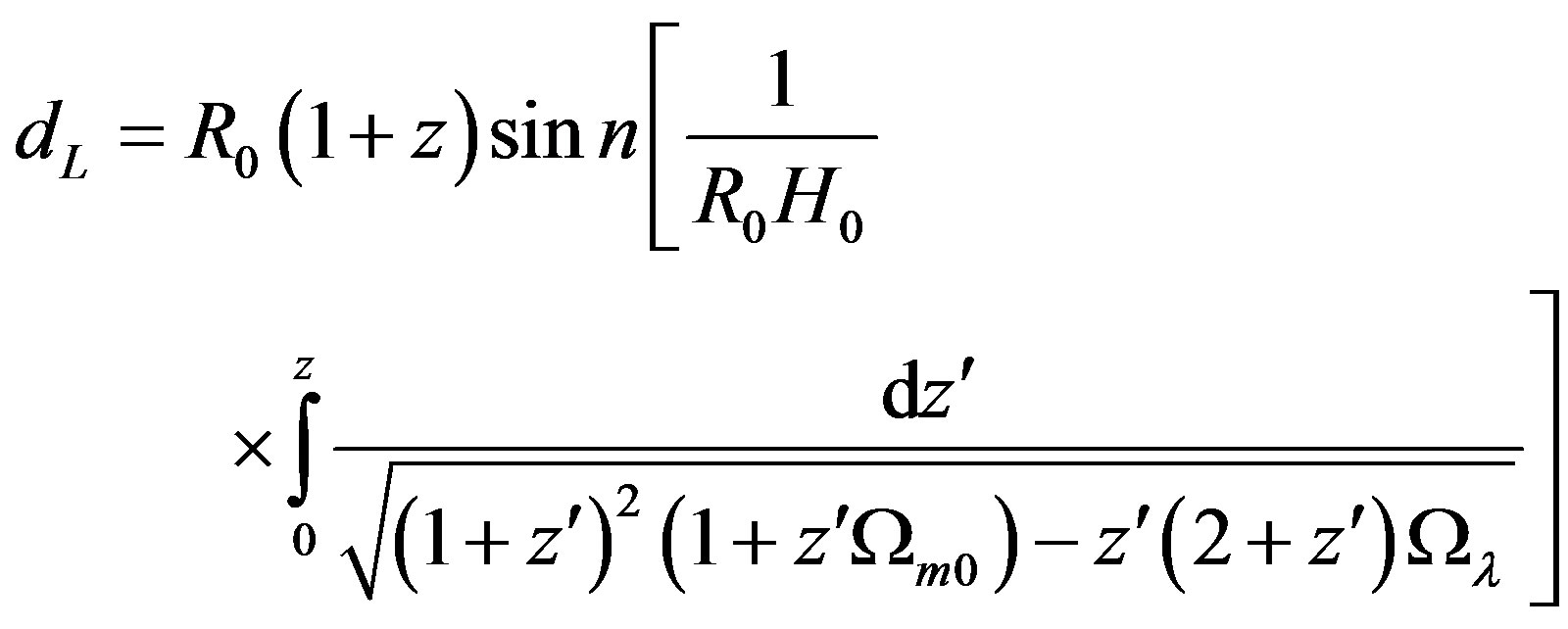 (50)
(50)
When space is flat, we have ,
,  , and
, and . So (50) becomes
. So (50) becomes
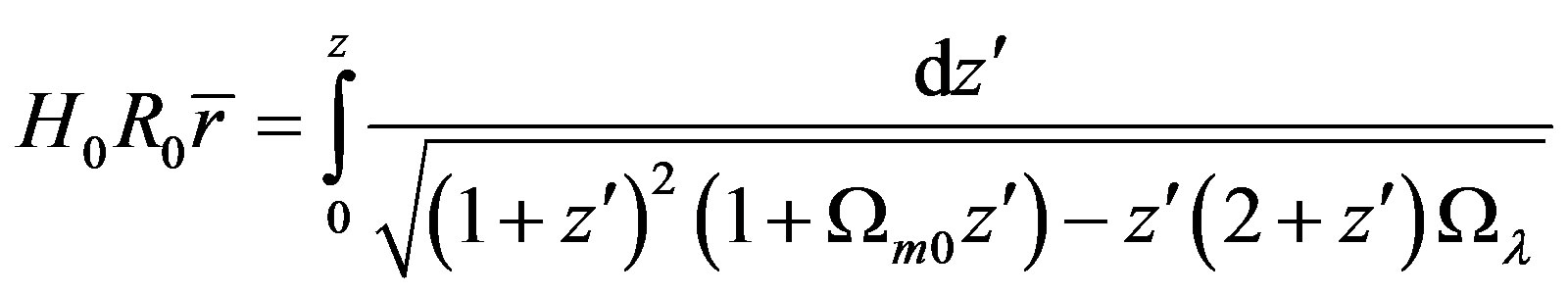 (51)
(51)
Comparing with (49), (51) has an additional item containing  in the radical sign of integrated function. The reason is that when
in the radical sign of integrated function. The reason is that when , the right side of (43) has only two items with
, the right side of (43) has only two items with
 (52)
(52)
But (36) is calculated without considering this factor, so that additional three items are added. If space is curved for , we still have
, we still have  and can obtain
and can obtain
 (53)
(53)
Similarly, for , we have
, we have
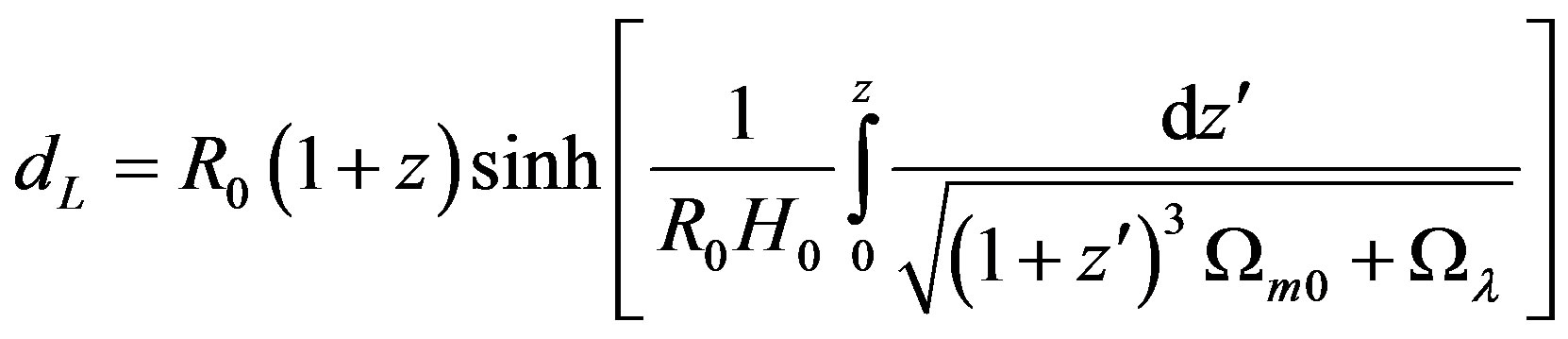 (54)
(54)
(53) and (54) are also different from (36), so (36) is wrong. Note that this is a mistake of mathematics, and has nothing to do with physics. So we can not use it to calculate the relation of red shift and distance of Ia supernova. More essential, if , we have
, we have . Substituting it in (44), we can not obtain (36). In this case, let
. Substituting it in (44), we can not obtain (36). In this case, let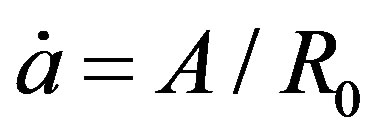 , substitute it in (44), for
, substitute it in (44), for , we obtain
, we obtain 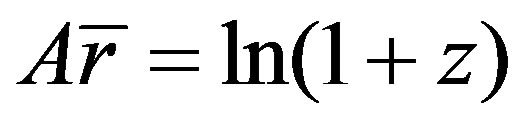 without practical significance.
without practical significance.
It is proved below that if the Doppler’s formula is used for calculation, the hypotheses of dark energy and the accelerated universe will become unnecessary.
3. Using the Doppler’s Formula to Calculate the Red Shift of Ia Supernova
3.1. The Friedmann Equation Needs Relativity Revision
Standard cosmology is based on the principle of cosmology. The principle declares that the distribution of universal material is uniform and isotropous. So the material density is only related to time and unrelated to spatial coordinates with the form . To match with the principle, the R-W metric is used in cosmology which is considered with biggest symmetry of space-time.
. To match with the principle, the R-W metric is used in cosmology which is considered with biggest symmetry of space-time.
Standard cosmology uses the Friedmann equation as basic equation. The Friedmann equation is based on the Einstein’s equation of gravity field. But two simplified conditions are used. One is the R-W metric and another is static energy momentum tensors. However, British physicist E. A. Milne proved in 1943 that the Friedmann equation could be deduced simply based on the Newtonian theory of gravity when cosmic constant is not considered [6]. This result indicates that the Friedmann equation is actually equivalent to the Newtonian theory of gravity which is only suitable to describe the universal processes with low expansion speed, unsuitable for the universal processes with high expansion speed. So we have to consider the rationality of these two simplified condition.
In fact, as discussed before, the R-W metric violates the invariability principle of light’s speed in vacuum and is not the metric of relativity. Static energy momentum tensor means that the velocity and momentum of celestial body which exist practically in the expansion process of the universe are neglected. So the Friedmann equation is one which is improperly simplified. In the early period of cosmology, what observed were the expansion processes with low speed nearing the Milky Way galaxy, the Friedmann equation can handle it. While cosmology develops to the current period, what observed are the expansion processes with high speed such as the red shift of Ia supernova, the Friedmann equation becomes unsuitable and need relativity revision [7].
If we use metric (33) which satisfies the constrain of special relativity in the Einstein’s equation of gravity, because metric tensors  and
and  contain speed factor
contain speed factor , the obtained cosmic equation is much more complicated than the Friedmann equation. If dynamic energy momentum tensor means are used simultaneously, speed factor
, the obtained cosmic equation is much more complicated than the Friedmann equation. If dynamic energy momentum tensor means are used simultaneously, speed factor  is also introduced. In this case, even though we consider the principle of cosmology to take material density as
is also introduced. In this case, even though we consider the principle of cosmology to take material density as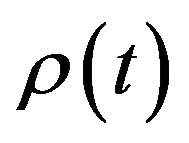 , the equation of cosmology will becomes very complex so that it is impossible to solve [7]. This may be the real reason why the pioneers of cosmology had to use the R-W metric and static energy momentum tensor, for they had no another choice.
, the equation of cosmology will becomes very complex so that it is impossible to solve [7]. This may be the real reason why the pioneers of cosmology had to use the R-W metric and static energy momentum tensor, for they had no another choice.
By considering this difficulty, we have to look for other more proper method to study cosmology. In fact, we have proved that by transforming the geodesic equation of the Schwarzschild solution of the Einstein’s equation of gravity field to flat space-time description, the following revised Newtonian formula of gravity can be obtained [7]
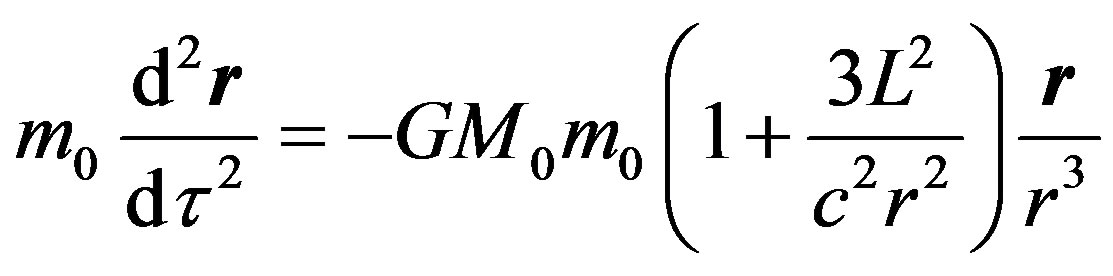 (55)
(55)
In (55) all quantities are defined in flat space. We have
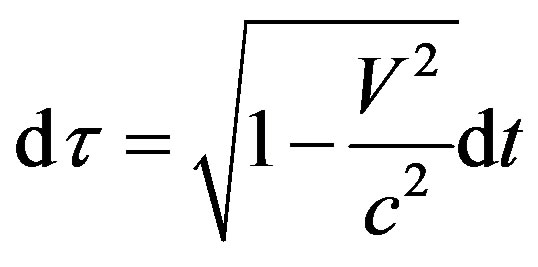 (56)
(56)
This is just the time delay formula of special relativity, so (55) can be considered as the relativity revision formula of the Newtonian gravity. The space-time singularity in the Einstein’s theory of gravity becomes the originnal point 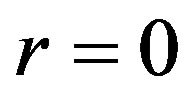 in the Newtonian formula of gravity. The singularity problem of general relativity in curved space-time is eliminated thoroughly. The theory of gravity returns to the traditional form of dynamic description.
in the Newtonian formula of gravity. The singularity problem of general relativity in curved space-time is eliminated thoroughly. The theory of gravity returns to the traditional form of dynamic description.
When the formula is used to describe the universe expansion, the revised Friedmann equation can be obtained. Based on it, the high red-shift of Ia supernova can be explained well. We do not need the hypotheses of the accelerating universe and dark energy. It is also unnecessary for us to assume that non-baryon dark material is 5 - 6 times more than normal baryon material in the universe if they really exist. The problem of the universal age can also be solved well.
Further more, we prove below that by the method of numerical calculation and the Doppler’s formula proposed in [7], even based on the Newtonian theory of gravity, we can also explain well the relation of red shift and distance of Ia supernova.
3.2. Using the Doppler’s Formula to Calculate the Red Shift of Ia Supernova
As we know that the solution of differential equation is determined by initial condition. However, according to the Big Bang theory, the universe blew up from a singularity with infinite density. That is to say, all material in the universe has a same initial position. However, infinite density is unimaginable and singularity can not exist in the real world. The practical situation may be that some unknown interactions can avoid material to be compressed into infinite density by gravity.
According to [7], we assume that there exist a certain mechanism so that a uniform material sphere with mass  can only be compress into a finite radius
can only be compress into a finite radius . The motion equation of universe expansion can be written as
. The motion equation of universe expansion can be written as
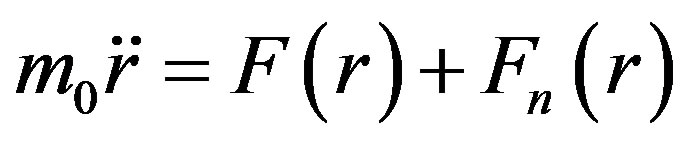 (57)
(57)
Here  is the Newtonian gravity and
is the Newtonian gravity and  is the sum of all non-gravities. For convenience of calculation, we assume
is the sum of all non-gravities. For convenience of calculation, we assume
 (58)
(58)
Here  is an unknown function.
is an unknown function.  corresponds to an infinite barrier at position
corresponds to an infinite barrier at position . When a material sphere with radius
. When a material sphere with radius  is compressed into a sphere with radius
is compressed into a sphere with radius , it can not be compressed further. For the spheres with different radii
, it can not be compressed further. For the spheres with different radii , their
, their  are different.
are different.
Suppose that the material distribution of the universe is uniform with . The static mass contained in the spherical surface with radius
. The static mass contained in the spherical surface with radius  is
is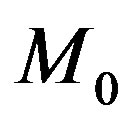 . According to (55), the revised Newtonian gravity is related to velocity. Using it to calculate the universe expansion, under the condition
. According to (55), the revised Newtonian gravity is related to velocity. Using it to calculate the universe expansion, under the condition , the speed of a particle located on the spherical surface is
, the speed of a particle located on the spherical surface is
 (59)
(59)
Here .
.  is a constant which describes initial conditions. Let
is a constant which describes initial conditions. Let 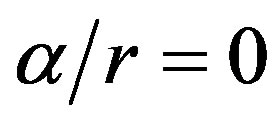 in (59), we get the result of the Newtonian theory of gravity
in (59), we get the result of the Newtonian theory of gravity
 (60)
(60)
We take an expansive sphere as the expansive universe and use the Doppler’s formula to describe red shift with
 (61)
(61)
Suppose that luminous body moves along the direction of radius and observer is located at the origin point of flat reference frame. The distance between observer and celestial body is 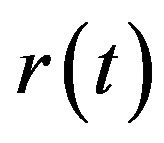 at moment
at moment . The distance between observer and celestial body is
. The distance between observer and celestial body is  at present moment
at present moment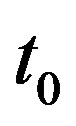 . In the expanding process of the universe, celestial body moves from
. In the expanding process of the universe, celestial body moves from  to
to  with
with , while the light travels from
, while the light travels from  to observer along opposite direction. Suppose that light’s speed is invariable in the process (having nothing to do with the speed of light’s source or the expensive speed of space, as shown in (30)), we have following relation
to observer along opposite direction. Suppose that light’s speed is invariable in the process (having nothing to do with the speed of light’s source or the expensive speed of space, as shown in (30)), we have following relation
 (62)
(62)
By astronomical observations, we know the universe material density 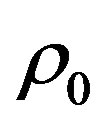 at present time
at present time , but we do not know
, but we do not know 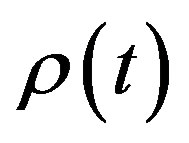 at past time
at past time . By the relation
. By the relation , we have
, we have
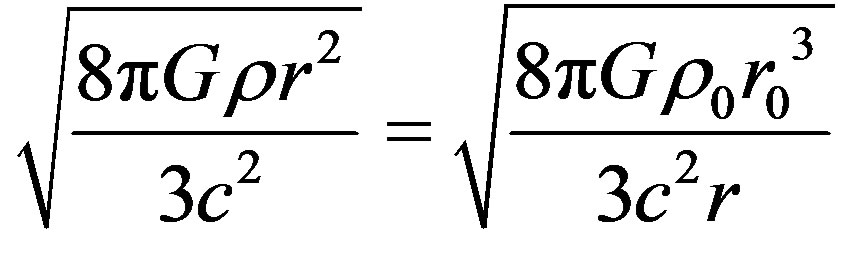 (63)
(63)
Substituting (60) in (62) and using (63), we obtain
 (64)
(64)
In principle, we can write (64) as
 (65)
(65)
From (65), we can get 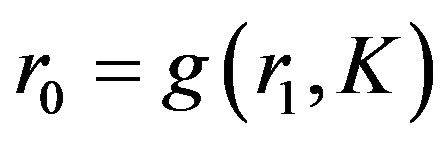 in principle. What observer see at present time is the light emitted by the celestial body located at position
in principle. What observer see at present time is the light emitted by the celestial body located at position  and time
and time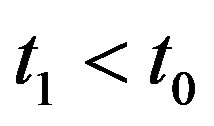 . At present time
. At present time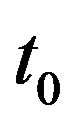 , the celestial body has moved to position
, the celestial body has moved to position .
.
In the formulas above, 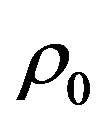 ,
,  and
and  are known through observations, but
are known through observations, but  and
and  are unknown. By connecting (60), (61) and (65), we can determinate
are unknown. By connecting (60), (61) and (65), we can determinate  and
and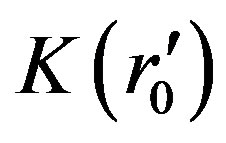 . The integral of (64) is difficult but can be calculated by the numerical method of computer. Take
. The integral of (64) is difficult but can be calculated by the numerical method of computer. Take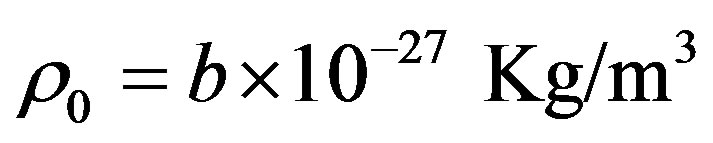 ,
, ,
,
 , we have
, we have
 (66)
(66)
We use  as basic variable to calculate
as basic variable to calculate 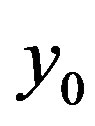 and
and . In the calculation, we take
. In the calculation, we take ,
,  and
and  as input parameters. With this method, we actually traced back to the initial situations of the universe expansion based on the present observations of red shift and distances. In other words, as long as the initial conditions of the universe expansion are known, we can know its current situations.
as input parameters. With this method, we actually traced back to the initial situations of the universe expansion based on the present observations of red shift and distances. In other words, as long as the initial conditions of the universe expansion are known, we can know its current situations.
3.3. The Red Shift of Ia Supernova
According to photometry measurement, the density of luminous material in the university is about  kg/m3 at present time. Because there exists a great mount of non-luminous material, we assume that practical material is 10 times more than luminous material and let
kg/m3 at present time. Because there exists a great mount of non-luminous material, we assume that practical material is 10 times more than luminous material and let  kg/m3. In Figure 1, we take mB = 5.5 + 5log dL in which
kg/m3. In Figure 1, we take mB = 5.5 + 5log dL in which  is luminosity distance with unit length
is luminosity distance with unit length . Because our discussion is based on flat space-time and the Doppler’s effect without considering the gravity red shift in this paper, light’s frequency does not change in the process of propagation. It is unnecessary for us to use the concept of luminosity distance (See appendix for detail). So we need to transform
. Because our discussion is based on flat space-time and the Doppler’s effect without considering the gravity red shift in this paper, light’s frequency does not change in the process of propagation. It is unnecessary for us to use the concept of luminosity distance (See appendix for detail). So we need to transform  back to practical distance
back to practical distance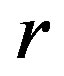 .
.
The curved line in Figure 2 shows the relations between the red-shifts, distances and initial condition parameters of Ia supernova based on the unrevised Newtonian formula of gravity. The vertical coordinate is the values of . The bottom horizontal coordinate is the value of red-shift. On the upside, under the line of horizontal coordinate, the numbers are the values of distance
. The bottom horizontal coordinate is the value of red-shift. On the upside, under the line of horizontal coordinate, the numbers are the values of distance . Above the line of horizontal coordinate, the numbers are the values of
. Above the line of horizontal coordinate, the numbers are the values of . For
. For  and
and , we get
, we get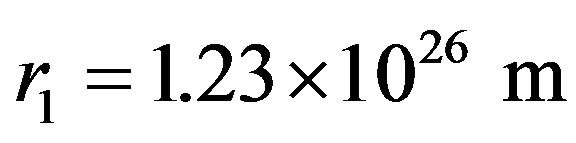 . By numerical calculation, we obtain
. By numerical calculation, we obtain 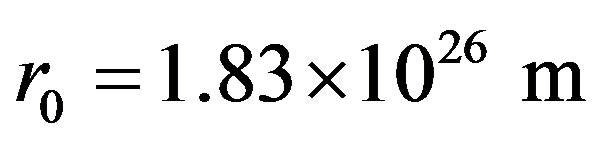 and
and . For
. For  and
and  corresponding to
corresponding to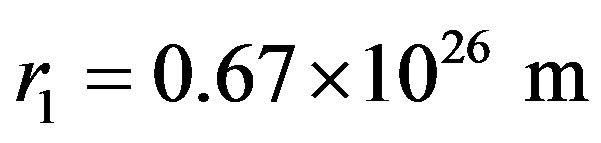 , we obtain
, we obtain  and
and . For
. For  and
and  which corresponds to
which corresponds to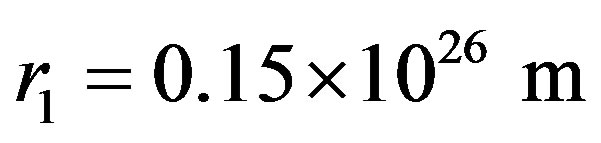 , we obtain
, we obtain  and
and .
.
We see that by directly using the Doppler’s formula and the Newtonian formula of gravity, we can explain the high red shift of Ia supernova well. The hypotheses of dark energy and the accelerating expansion of the universe become unnecessary. The universe began its expansion from a finite volume, rather than a singularity. The difficulty of singularity in cosmology is eliminated.
If the revised Newtonian formula (55) is used, according to reference [7], the result is shown in Figure 3. Comparing Figures 2 and 3, the difference is that for the Newtonian formula of gravity, we have . But for the revised Newtonian formula of gravity, we have
. But for the revised Newtonian formula of gravity, we have  when
when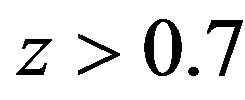 , and
, and 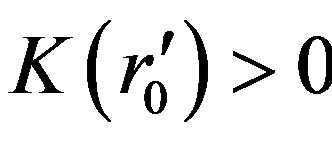 when
when . When
. When  is very small, we have
is very small, we have  for both situations.
for both situations.
3.4. The Age of the Universe
We consider the universe as a material sphere with radius  at initial moment, which is about the distance between the sun and the earth. Long enough later, at time
at initial moment, which is about the distance between the sun and the earth. Long enough later, at time , an observer located at the original point of reference frame receives the light emitted from a celestial body on the spherical surface with radius r = 1.23 × 1026 m and red shift
, an observer located at the original point of reference frame receives the light emitted from a celestial body on the spherical surface with radius r = 1.23 × 1026 m and red shift  at time
at time . Suppose that
. Suppose that

Figure 1. The Hubble diagram for red shift and distance of Ia supernova.

Figure 2. The relations between red-shifts, distances and initial parameters of Ia supernova by using the Doppler’s formula and the Newtonian gravity.

Figure 3. The relations between red-shifts, distances and initial parameters of Ia supernova by using the Doppler’s formula and the revised Newtonian gravity.
the material density of the universe is  kg/m3 at present time, the initial density is
kg/m3 at present time, the initial density is  kg/m3, to be equal to the density of neutron star. According to the calculation before, the real distance of celestial body is
kg/m3, to be equal to the density of neutron star. According to the calculation before, the real distance of celestial body is  at present time. We consider it as the radius of observable universe and take
at present time. We consider it as the radius of observable universe and take 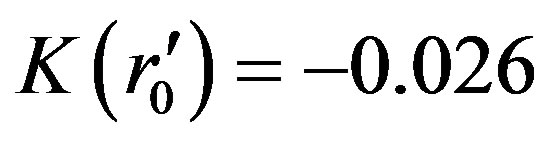 for the following formula to calculate the time during which the universe expanded from radius
for the following formula to calculate the time during which the universe expanded from radius 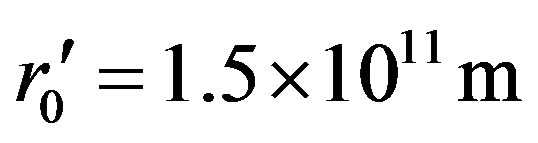 to r0 = 1.83 × 1026 m
to r0 = 1.83 × 1026 m
 (67)
(67)
The result is 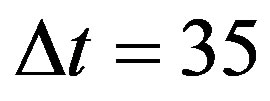 billion years. But this value is not sensitive to
billion years. But this value is not sensitive to  when it is not very large. Taking
when it is not very large. Taking , which is about the radius of the Milky Way galaxy, the result is almost the same with
, which is about the radius of the Milky Way galaxy, the result is almost the same with  m. It means that the age of the universe mainly depends on the later expansive process. Using (67) to calculates the time during which the radius of sphere expanses from
m. It means that the age of the universe mainly depends on the later expansive process. Using (67) to calculates the time during which the radius of sphere expanses from  to
to , the result is 15.4 billion years, so the time during which the radius of sphere expanses from
, the result is 15.4 billion years, so the time during which the radius of sphere expanses from  to
to  is 19.5 billion years.
is 19.5 billion years.
By using the revised Newtonian formula of gravity, for the same red shift , the result in reference [8] is that the time is 30.8 billion years for a sphere’s radius expands from
, the result in reference [8] is that the time is 30.8 billion years for a sphere’s radius expands from 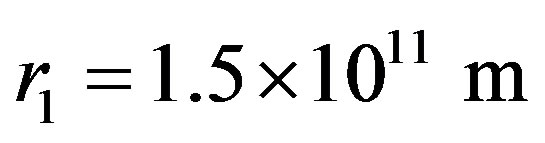 to
to  and 13 billion years for radius expands from
and 13 billion years for radius expands from  to
to . So the sphere’s radius expands from
. So the sphere’s radius expands from  to
to  is 17.8 billion years.
is 17.8 billion years.
Therefore, for the same red shift, by using the revised Newtonian gravity, the age of the universe is smaller then using the unrevised Newtonian gravity. According to the current cosmology, the universe age is estimated to be about 10 - 15 billion years, too short to the formation of galaxies. The problem does not exist by using the Doppler’s formula to calculate the red shift of cosmology, no mater we use the revised Newtonian formula or the unrevised Newtonian formula of gravity.
4. Conclusions
There are many difficulties in the current cosmology. They are essential and can not be solved by some small revising. We need to suspect whether or not there are problems in the foundation of cosmology. In the process of deducing the Friedmann equation of cosmology based on the Einstein’s equation of gravity, two simplification conditions are used. One is the R-W metric, in which metric tensors are only related to time, not related to space coordinates. Another is static energy momentum tensors, in which celestial body’s velocities are neglected. We need to discuss whether or not these two conditions are proper, for they are really over simplified.
Cosmic red shift is considered to be caused by the receding motions of celestial bodies which are actually the Doppler’s effect. However, in the current cosmology, what used to calculate the relation of red shift and distance of Ia supernova is the formula of metric red shift based on the R-W metric, rather than the formula of the Doppler’s red shift. They are completely different and the inconsistence can not be allowed in physics. We should consider why the metric red shift is used rather than the Doppler’s red shift in cosmology.
The reason is that the Doppler’s effect is related to speed factor . If the Doppler’s effect is used directly, we should use dynamic energy momentum tensor in the Einstein’s equation of gravity too. In this case, because speed factor
. If the Doppler’s effect is used directly, we should use dynamic energy momentum tensor in the Einstein’s equation of gravity too. In this case, because speed factor  is contained in energy momentum tensor, the obtained equation of cosmology would become too complex to be solved. If the metric red shift formula is used, it is equivalent to use static energy momentum tensor, the trouble can be avoided. However, the problem is that there exist relative motion speeds practically between observers at rest on the earth and celestial bodies. So it is very irrational to use static energy momentum tensors in cosmology.
is contained in energy momentum tensor, the obtained equation of cosmology would become too complex to be solved. If the metric red shift formula is used, it is equivalent to use static energy momentum tensor, the trouble can be avoided. However, the problem is that there exist relative motion speeds practically between observers at rest on the earth and celestial bodies. So it is very irrational to use static energy momentum tensors in cosmology.
In order to avoid using dynamic metric, co-moving coordinate system is used by expansion cosmology. Because observer moves with celestial body in co-moving coordinates system, the speed of celestial body can be eliminated. However, there are three problems here. The first is that astronomers at rested on the earth observe red shift without moving with celestial body. The second is that even though the observer moves with a celestial body, because the speed of expansion is related to the distance between celestial bodies, the relative speeds between the observer and other celestial bodies still exist. The third is that if observer moves with celestial body, it means that observer falls freely in gravitational field. According to the principle of general relativity, gravity is canceled locally. In this case, the metric of space-time is flat and all calculations about cosmic red shift become ineffective.
On the other hand, the formula of metric red shift based on the R-W metric is impossible. The reason is the R-W metric is only a mathematical structure of space. It is not absolutely necessary to use the R-W metric in cosmology. In fact, we can also use common coordinate system to establish cosmic equation based on the Einstein’s equation of gravity. So the origin of metric red shift is suspicious. At least, it is not an independent effect caused by independent physical mechanism. But gravity red shift and the Doppler’s red shift are caused by independent physical laws. If we can obtain red shift from the R-W metric, it should not be contradicted with gravity red shift or the Doppler’s red shift. Otherwise, it is unacceptable.
It is proved strictly that Formula (1) is only the result of first order approximation. When higher order approximations are taken into account, the constriction condition  can be obtained. Therefore, Formula (1) is only suitable to describe the process of spatial uniform expansion; it’s unsuitable for the practical process of the universal expensive with acceleration. More strictly, if we do not consider approximation, both relations the formula (6) and (15) do not exist. That is to say, we have no metric red shift actually.
can be obtained. Therefore, Formula (1) is only suitable to describe the process of spatial uniform expansion; it’s unsuitable for the practical process of the universal expensive with acceleration. More strictly, if we do not consider approximation, both relations the formula (6) and (15) do not exist. That is to say, we have no metric red shift actually.
Besides, the R-W metric has many other problems. It is proved that the R-W metric violates the principle of light’s speed invariable. When  is related to time, the R-W metric has no constant curvature. The time delay caused by relativity velocity between light’s source and observer is neglected according to the R-W metric. So the R-W metric is not a relativity one and unsuitable to be used as the basic space-time frame in cosmology. The red shift based on it can not be correct.
is related to time, the R-W metric has no constant curvature. The time delay caused by relativity velocity between light’s source and observer is neglected according to the R-W metric. So the R-W metric is not a relativity one and unsuitable to be used as the basic space-time frame in cosmology. The red shift based on it can not be correct.
Therefore, the current formula used to calculates the relation of red shift and distance of Ia supernova in cosmology is wrong. We should directly use the Doppler’s formula to calculate the red shift of cosmology. By the method of numerical calculation, based on the (revised) Newtonian theory of gravity and the Doppler’s formula, it is proved that the red shift of Ia supernova can be explained well. Therefore the hypotheses of dark energy and the accelerating universe are completely unnecessary. The problems of the universe age and the singularity of the Big Bang in the early universe can also be solved simultaneously. In fact, the so-called accelerating expansion of the universe is not the result of direct observation. It depends on the fitting between theoretical modal and the observation of Ia supernova. Other proofs of the accelerating universe such as the cosmic background radiation anisotropy and the X ray properties of galaxy clusters and so on are not direct ones, or can be explained by other methods shown in this paper. They remain to be discussed further. The hypothesis of accelerating universe is completely unnecessary.
The procedure we developed and used in this paper and its source code are open to researchers. Demanders, please send us e-mail to ask for it.
Appendix: Inconsistence between the R-W Metric and the Doppler’s Red Shifts
1. Proper Distance and Expansive Speed Based on the R-W Metric
The standard cosmology uses the R-W metric (2) to describe the universal space-time. According to the R-W metric, at a certain moment , the proper distance between a celestial body and the original point of coordinate system is [9]
, the proper distance between a celestial body and the original point of coordinate system is [9]
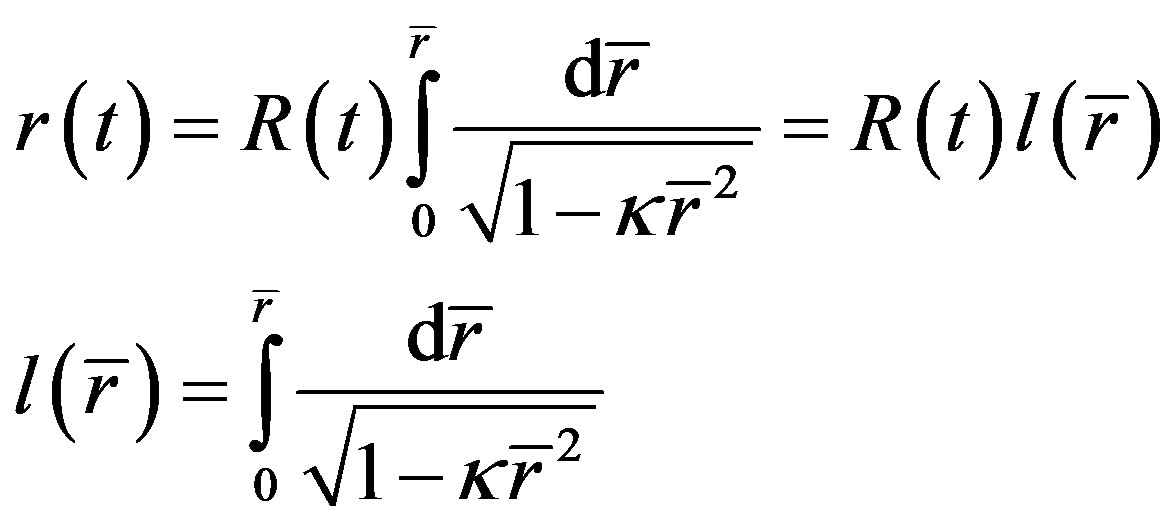 (68)
(68)
If space is flat with , we get
, we get  and
and
 (69)
(69)
Suppose that observer is at the original point of coordinates system and space is flat, due to spatial expansion, the speed of celestial body relative to observer is
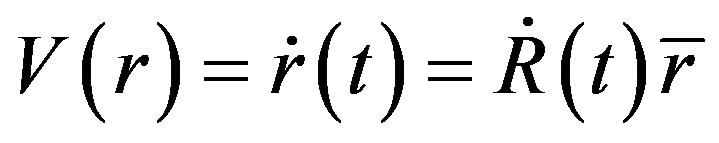 (70)
(70)
It is a wrong understanding in cosmology that celestial bodies have no velocities when co-moving coordinates are used. In fact, if , there is certainly a relative velocity according to (70).
, there is certainly a relative velocity according to (70).
The speed shown in (70) is proportional to . For a certain
. For a certain , when
, when  is large enough, we could have
is large enough, we could have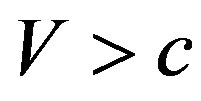 . This result will cause a great trouble for cosmology. Many problems in the current cosmology are related to it. In the early period of cosmology, because the speeds of observed celestial bodies are low with
. This result will cause a great trouble for cosmology. Many problems in the current cosmology are related to it. In the early period of cosmology, because the speeds of observed celestial bodies are low with , (70) is tenable approximately. In fact, the Hubble formula is related to (70). However, if the distance is large enough, the inadaptability of (70) will emerge.
, (70) is tenable approximately. In fact, the Hubble formula is related to (70). However, if the distance is large enough, the inadaptability of (70) will emerge.
2. Luminosity Distance and Proper Distance
The distances of celestial bodies can not be measured directly in general. The indirect methods are needed and the concept of luminosity distance is used. The energy that celestial body emitted in unit time is called as luminosity . What measured in astronomy is its brightness
. What measured in astronomy is its brightness . Let
. Let  represent luminosity distance, their relation is
represent luminosity distance, their relation is . Suppose that a celestial body emitted
. Suppose that a celestial body emitted 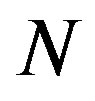 photons at time
photons at time 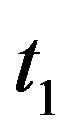 with frequeNcy
with frequeNcy , we have
, we have . During the time
. During the time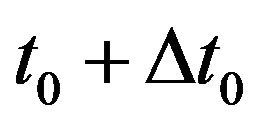
 , these photon arrive at the spherical surface with radius
, these photon arrive at the spherical surface with radius 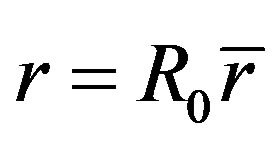 and the frequency becomes
and the frequency becomes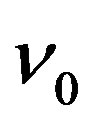 , we have
, we have . So we get
. So we get
 .
.
If space-time is flat with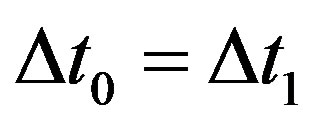 , we have
, we have . If light’s frequency does not change with
. If light’s frequency does not change with  when it propagates in space, luminosity distance is equal to real distance. For example, as shown in this paper, light’s source moves in flat space and we only consider the Doppler’s shift. In this case, the light’s frequency is unchanged and we can take
when it propagates in space, luminosity distance is equal to real distance. For example, as shown in this paper, light’s source moves in flat space and we only consider the Doppler’s shift. In this case, the light’s frequency is unchanged and we can take .
.
3. The Doppler’s Red Shift
Suppose that luminous celestial body is at rest in reference frame , the emitted light’s proper frequency and wave length are
, the emitted light’s proper frequency and wave length are  and
and . Reference frame
. Reference frame  moves in a uniform speed
moves in a uniform speed  relative to
relative to . Observing in
. Observing in , the received light’s frequency and wave length become
, the received light’s frequency and wave length become 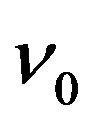 and
and . The definition of frequency shift is
. The definition of frequency shift is
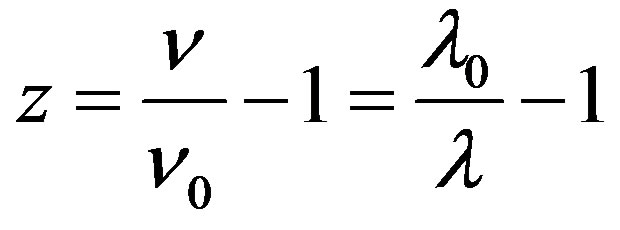 (71)
(71)
If  moves apart from
moves apart from  along the radial direction with speed
along the radial direction with speed , according to the Doppler’s formula, the red shift is
, according to the Doppler’s formula, the red shift is
 (72)
(72)
The Doppler’s frequency shift is only related to speed, having noting to do with distance. As along as light is emitted, no matter how far the observers are, received frequencies are the same. In this sense, the metric red shift is completely different fundamentally from the Doppler’s red shift.
4. The Hubble Red Shift
Suppose that there is no gravitational field in space or space is flat, light’s frequency does not change in its propagation process, so luminosity distance is equal to practical distance. By introducing coordinate transformation  which is so called space expansion and define the Hubble constant
which is so called space expansion and define the Hubble constant , the Hubble red shift is
, the Hubble red shift is
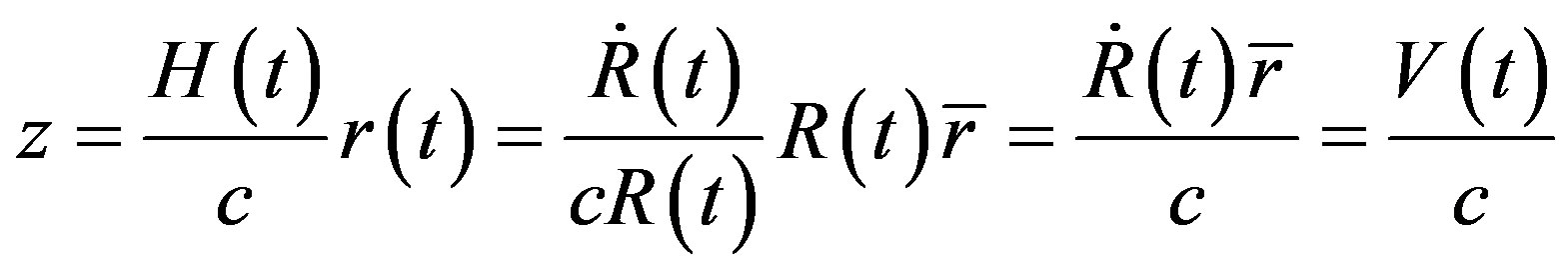 (73)
(73)
Comparing (73) with (72), it is obvious that the Hubble formula is the approximation of the Doppler’s formula under the condition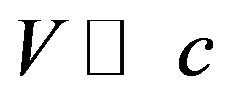 . It seems that the Hubble red shift is proportional to distance
. It seems that the Hubble red shift is proportional to distance . However, because the Hubble constant contains speed factor
. However, because the Hubble constant contains speed factor  actually, the formula is related to velocity essentially. In fact, the Hubble red shift is considered to be caused by the recession velocity of celestial body. In this way, the universal expansion is deduced. The red shift observed in cosmology is also related to gravity. Strictly speaking, we should consider both the Doppler’s and gravitational red shifts simultaneously in cosmology.
actually, the formula is related to velocity essentially. In fact, the Hubble red shift is considered to be caused by the recession velocity of celestial body. In this way, the universal expansion is deduced. The red shift observed in cosmology is also related to gravity. Strictly speaking, we should consider both the Doppler’s and gravitational red shifts simultaneously in cosmology.
5. The Red Shift Caused by the R-W Metric
As shown in Figure 4, suppose that a luminous celestial body is located at position  at moment
at moment . The frequency of emitted light is
. The frequency of emitted light is . The observer at original point
. The observer at original point  receives the light at moment
receives the light at moment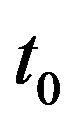 . The frequency of received light is
. The frequency of received light is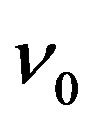 . Suppose that light source emits another light in time interval
. Suppose that light source emits another light in time interval  with period
with period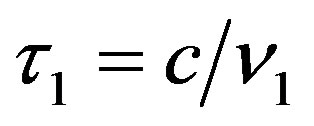 . If the light is received by observer located at original point
. If the light is received by observer located at original point  at moment
at moment , the frequency of received light is
, the frequency of received light is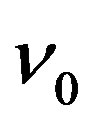 .
.
According to Figure 4 and based on the R-W metric, we can obtain (1) which is related to scalar  and not related to the speed factor
and not related to the speed factor  of spatial expansion. But the Doppler’s red shift is related to
of spatial expansion. But the Doppler’s red shift is related to , having nothing to do with
, having nothing to do with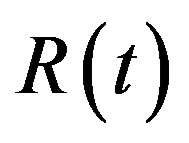 . Both are completely different.
. Both are completely different.
Let’s discuss the real meaning of Formula (1) now. In order to determine red shift, we have to know  and
and . Because we determine
. Because we determine  by measurement, the key is to determine
by measurement, the key is to determine . In practice,
. In practice, 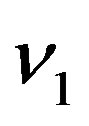 is considered as light’s proper frequency. Suppose that there is no gravity field in space without gravity red shift. Suppose that there is an observer located at point
is considered as light’s proper frequency. Suppose that there is no gravity field in space without gravity red shift. Suppose that there is an observer located at point  who is at rest with light’s source. According to this observer, light’s frequency is
who is at rest with light’s source. According to this observer, light’s frequency is , i.e., proper frequency. When light travels from
, i.e., proper frequency. When light travels from  to original point
to original point , frequency changes from
, frequency changes from  to
to . That is to say, the change of frequency is caused by the distance between light’s source and observer, rather than the speed of light’s source. This is just the essence of metric red shift.
. That is to say, the change of frequency is caused by the distance between light’s source and observer, rather than the speed of light’s source. This is just the essence of metric red shift.
However, this idea will cause serious problem, inconsistent with the Doppler’s red shift. According to observer at original point , the celestial body at point has a moving speed. The frequency of light emitted by the celestial body is not proper frequency with the Doppler’s red shift. The change of frequency is related to speed and not related to distance. In fact, if frequency is related to distance, when a static observer measure the frequency of light emitted by a static light’s source in distance, red shift would be founded. Obviously, this result violates experiments and basic physical laws and is completely impossible. So the red shift caused by the spatial expansion can only be the Doppler’s red shift related to speed, rather than the metric red shift related to distance.
, the celestial body at point has a moving speed. The frequency of light emitted by the celestial body is not proper frequency with the Doppler’s red shift. The change of frequency is related to speed and not related to distance. In fact, if frequency is related to distance, when a static observer measure the frequency of light emitted by a static light’s source in distance, red shift would be founded. Obviously, this result violates experiments and basic physical laws and is completely impossible. So the red shift caused by the spatial expansion can only be the Doppler’s red shift related to speed, rather than the metric red shift related to distance.
If there is gravity field in space, according to general

Figure 4. The red shift caused by the R-W metric.
relativity, gravity will cause red shift. In this case, besides the Doppler’s red shift, we should consider gravity red shift too. Because the intensities of gravity are different in different places, 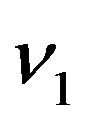 is related to the position where light’s source is located. So
is related to the position where light’s source is located. So 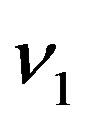 is not proper frequency again.
is not proper frequency again.
However, in practical observation, we can not measure the intensity of gravity field in distance place, so we do not know  actually. We only compare observed frequency
actually. We only compare observed frequency  with proper frequency to calculate red shift. So we can not used (1) to describe gravity red shift. In fact, if the universe is static, we have
with proper frequency to calculate red shift. So we can not used (1) to describe gravity red shift. In fact, if the universe is static, we have  and
and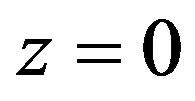 , even thought there exist gravity field and gravity red shift.
, even thought there exist gravity field and gravity red shift.
So metric red shift described by (1) is different from the Doppler’s shift and gravity red shift. It contradicts with the Doppler’s red shift. We take some concrete examples to prove this point further below.
6. The Red Shift in the Uniform Expansion Process of Space
The R-W metric can be used to describe both the uniform and accelerating expansion of space. The uniform expansion is equal to the uniform motion of light’s source. In this case,  is the proper frequency of light for the observer located at
is the proper frequency of light for the observer located at . For the observers at rest in
. For the observers at rest in , light’s proper frequency is also
, light’s proper frequency is also , but received frequency is
, but received frequency is . Let
. Let ,
,  and
and  are constants. The speed of spatial expansion is
are constants. The speed of spatial expansion is . According to the Doppler’s and Hubble’s formula, we have the same red shift
. According to the Doppler’s and Hubble’s formula, we have the same red shift
 (74)
(74)
The red shift is proportional to coordinate  (distance), having nothing to do with the time that light was emitted. The red shift is the same no matter what time observer observes. However, according to the metric red shift formula (1), we have
(distance), having nothing to do with the time that light was emitted. The red shift is the same no matter what time observer observes. However, according to the metric red shift formula (1), we have
 (75)
(75)
 represents the red shift that observer observes at moment
represents the red shift that observer observes at moment . The Hubble constant at moment
. The Hubble constant at moment  is
is
 (76)
(76)
The uniform expansion of space corresponds to the uniform motion of light’s source, and light’s speed is unrelated to the motion of light’s source, or light’s speed is invariable in vacuum. Let , in this case,
, in this case,  is just the distance between observer at original point and luminous celestial body at moment
is just the distance between observer at original point and luminous celestial body at moment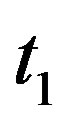 . Therefore, we can write (75) in the form of the Hubble’s red shift
. Therefore, we can write (75) in the form of the Hubble’s red shift
 (77)
(77)
It seems that (77) is the same as the Hubble’s formula. But it is different from (74) essentially. According to (74), red shift is proportional to  and is not a function of time. We observe at present time
and is not a function of time. We observe at present time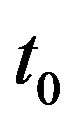 , and red shift is
, and red shift is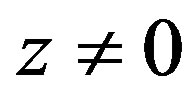 . According to (77), red shift is related to
. According to (77), red shift is related to . When
. When , the distance between light’s source and observer is zero, red shift is also zero even though the relative speed between them is non-zero.
, the distance between light’s source and observer is zero, red shift is also zero even though the relative speed between them is non-zero.
Speaking simply, according to the Doppler’s formula, red shift is related to the velocity of light source, having nothing to do with distance. When the distance is zero and light source’s speed is light’s speed, red shift infinite. According to the formula based on R-W metric, red shift is related to the distance, and unrelated to the velocity of light source. When the distance is zero and light source’s speed is light’s speed, red shift is still zero. The difference is so great and essential so that they can not be consistent at all.
7. The Red Shift in the Uniform Accelerating Expansion Process of Space
If light’s source is accelerated in vacuum, according to general relativity, non-inertial motion is equal to gravitational field and gravity red shift will be produced. Therefore, in this case, when luminous body moves in gravitational field, gravity red shift should also be considered. Because the red shifts are different in different places with different intensities of gravity, the frequency  of emitted light is different in different places. So
of emitted light is different in different places. So 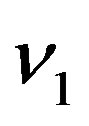 shown in (1) is not proper frequency again. The observer located at original point
shown in (1) is not proper frequency again. The observer located at original point  does not know the initial value
does not know the initial value . He can only compare received frequency
. He can only compare received frequency 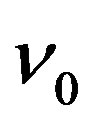 with proper frequency. So in this case, (1) has nothing to do with practical measurement. That is to say, if gravity or acceleration effects are considered, Formula (1) is unavailable.
with proper frequency. So in this case, (1) has nothing to do with practical measurement. That is to say, if gravity or acceleration effects are considered, Formula (1) is unavailable.
If gravity and acceleration effects are omitted, we discuss the differences between the Doppler’s and Hubble’s red shifts and the metric red shift. Suppose that space is flat, light’s source is uniformly accelerated with
 (78)
(78)
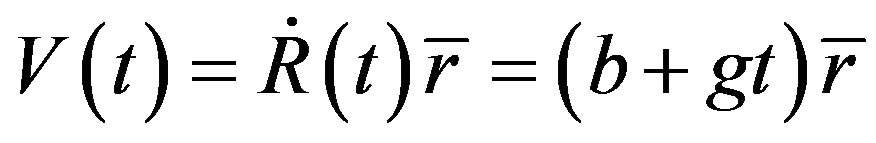 (79)
(79)
When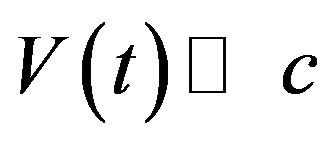 , the Doppler’s red shift at moment
, the Doppler’s red shift at moment 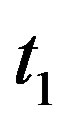 is
is
 (80)
(80)
Because acceleration effect has been omitted, light’s frequency is unchanged in the process of light’s propagation. The red shift observed by observer at original point at time  is also represented by (80). The Hubble constant at time
is also represented by (80). The Hubble constant at time  is
is
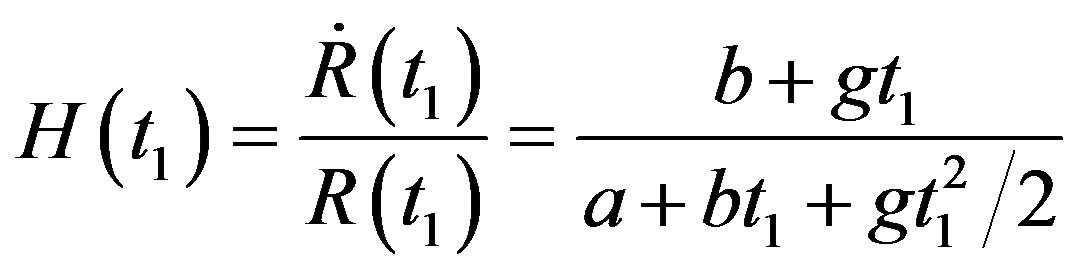 (81)
(81)
So the Hubble’s red shift is
 (82)
(82)
It is the same as the Doppler’s red shift (80). If we consider (1), the red shift becomes
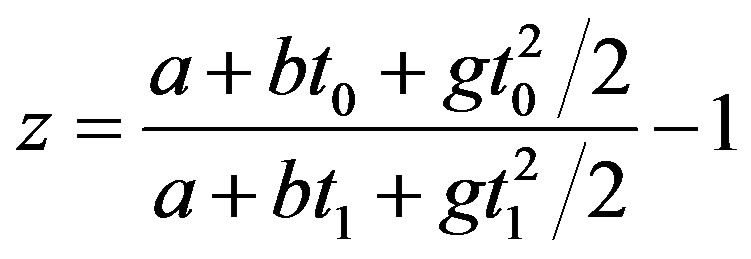 (83)
(83)
By using (81) and let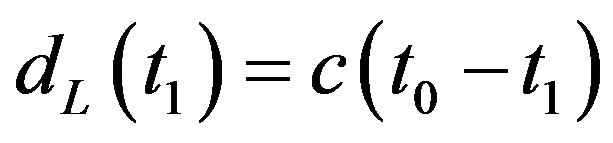 , we can write (82) as
, we can write (82) as
 (84)
(84)
This is considered as the revised Hubble formula in cosmology. In which  may not be the real distance of light’s source, we called it as apparent distance.
may not be the real distance of light’s source, we called it as apparent distance. 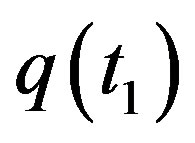 is the so-called decelerated factor with
is the so-called decelerated factor with
 (85)
(85)
(84) is completely different from (80) and (82), and they are incompatible. According to (80) and (82), red shift is still proportional to coordinate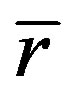 . At present moment, we have
. At present moment, we have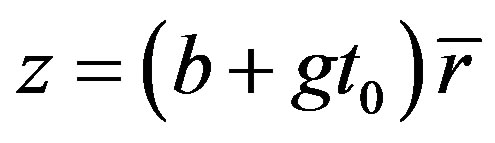 . But according to (84), the relation between red shift and
. But according to (84), the relation between red shift and  is not linear again. At present moment, we have
is not linear again. At present moment, we have , even though the relative speed between them may not be zero. It is obvious that the Doppler’s red shift and the Hubble’s red shift are consistent, but they are completely different from the metric red shift.
, even though the relative speed between them may not be zero. It is obvious that the Doppler’s red shift and the Hubble’s red shift are consistent, but they are completely different from the metric red shift.
8. The Red Shift of Metric in General Situations
If the acceleration of spatial expansion is arbitrary, according to standard theory, we develop 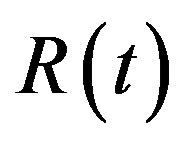 into the Taylor series in the neighborhood of
into the Taylor series in the neighborhood of  with [8]
with [8]
 (86)
(86)
Here the decelerated factor is
 (87)
(87)
If the items in the bracket of (86) are small enough, let  and substitute it in (1), we can obtain
and substitute it in (1), we can obtain
 (88)
(88)
(88) is considered as the revised Hubble formula, although  may not be the real distance of light’s source. However, the formula should satisfy the condition that
may not be the real distance of light’s source. However, the formula should satisfy the condition that  is small enough, otherwise the series is divergent. Besides, it should note that
is small enough, otherwise the series is divergent. Besides, it should note that  and
and  in (86) is the quantities at present time. But in (82) and (84),
in (86) is the quantities at present time. But in (82) and (84),  and
and  are the quantities at past time.
are the quantities at past time.
However, for the problems of cosmology,  may be very large. For example, for the supernova of high red shift,
may be very large. For example, for the supernova of high red shift,  may be billion years. Because the high order items in (86) are proportional to
may be billion years. Because the high order items in (86) are proportional to , when
, when , the formula is infinite, so it is unsuitable in general. In fact, as shown in (1), the positions of times
, the formula is infinite, so it is unsuitable in general. In fact, as shown in (1), the positions of times  and
and  are equal. We have two independent variables
are equal. We have two independent variables 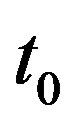 and
and  actually. When their difference is great, we can only develop
actually. When their difference is great, we can only develop  into the Taylor series in the neighborhood of
into the Taylor series in the neighborhood of 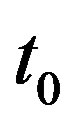 and develop
and develop  into the Taylor series in the neighborhood of
into the Taylor series in the neighborhood of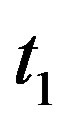 . The results should be
. The results should be
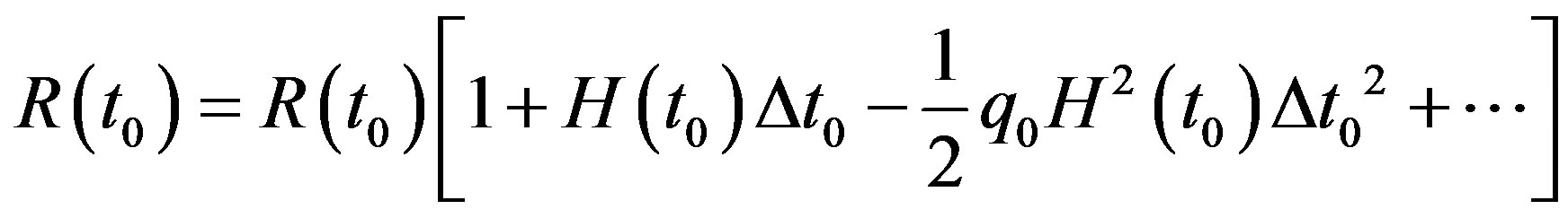 (89)
(89)
 (90)
(90)
Here  and
and . So (1) should be
. So (1) should be
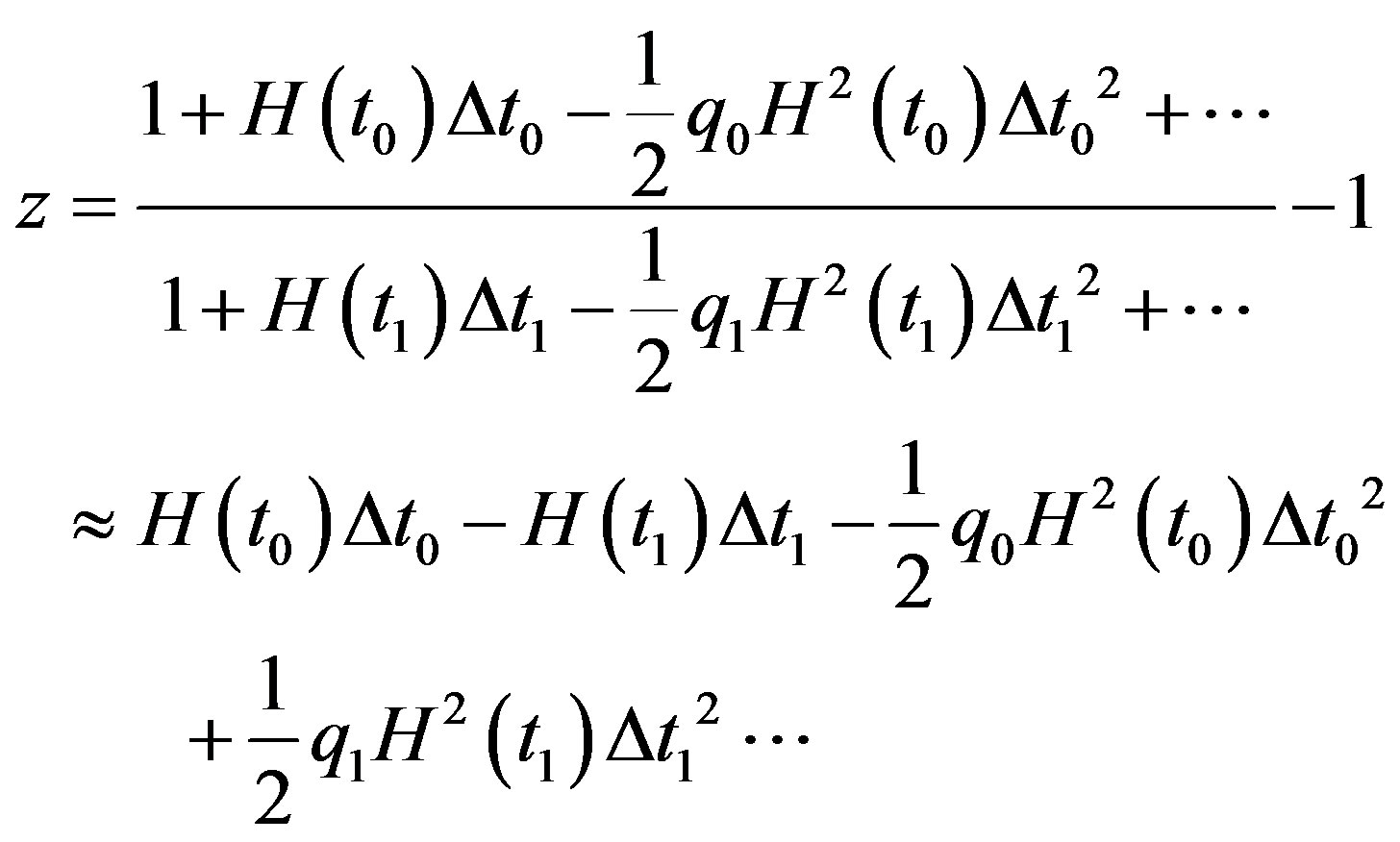 (91)
(91)
It is completely different from (88). That is to say, we can not obtain the revised Hubble’s formula (88) from the metric red shift formula (1) in general situations.