1. Introduction
It is known that if there exist a real division algebra then the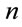 
-dimensional sphere 
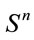in 
is parallelizable [1-3]. It is also known that the only parallelizable spheres are 
and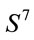 
[4] (see also Ref. [5]). So one concludes that division algebras only exist in 1, 2, 3 or 
dimensions (see Refs. [6-10] and references therein). It turns out that these theorems are deeply related to the Hopf maps, 
, 
and 
[4]. Focusing on
, it is intriguing that none of these remarkable results seem to have been considered in the proof the the original Poincaré conjecture [11-13], which establishes that any closed simply connected 3-manifold 
is homeomorphic to
. In fact, until now any proof of the Poincaré conjecture associated with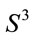 
is based in the Ricci flow equation [14] (see also Refs. [11-13]), but the parallelizabilty of 
(or any 
manifold) is not even mentioned. The main goal of this work is to establishes a link between the concept of parallelizability and the Ricci flow equation. We also explain a number of physical scenarios where such a link may be important, including special relativity, cosmology and Hopf maps via 
-qubit systems (see Ref. [15] and Refs. therein).
Before we address the problem at hand it is worth making a number of comments. Let us start mentioning that it has been shown that division algebras are linked to different physical scenarios, including, superstrings [16] and supersymmetry [17,18]. Even more surprising is the fact that division algebras are also linked to quantum information theory via the 
-qubit theory (see Refs. [19-21]). Mathematically, division algebras are also connected with important arenas such as K-theory [6]. If a division algebra is normed then one may also introduce the four algebras; real numbers, complex numbers, quaternions and octonions (see Ref. [10]). On the other hand the Poincaré conjecture seems to be useful in the discussion of various cosmological models (see Refs. [22-25]) and the study of gravitational instanton theory [26].
One may ask ourselves: Are all this links a coincidence? or there is in these links a deep underlying message? An indicator that starting with division algebras one may obtain a deep physical result is illustrated by superstrings. In fact, in this case the dimensionality of the spacetime it is not putted by hand but is a prediction of the theory. It turns out that at the quantum level one finds a consistent superstring theory only when the dimension of the spacetime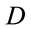 
takes values in the set
. Considering light-like coordinates such that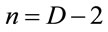 
one realizes that E can be reduced to the set
. But 
corresponds exactly to the only dimensions where a division algebra may exist (see Ref. [16] for details). From this perspective one may say that in a sense the dimensions where a quantum consistent superstring theory may exist are predicted by division algebras. Another scenario where the divisionalgebra/Poincaré-conjecture correspondence may play a physical important role is in instanton theory. In this case the Hopf maps determine the different structures of instanton solutions (see Ref. [26]).
Let us start introducing the metric tensor
(1)
Here, 
is a coordinate patch in a 
-dimensional manifold
. We also introduce a Riemann symmetric connection 
and the totally antisymmetric torsion tensor
. Geometric parallelizability of 
means the “flattening” the space in the sense that
(2)
where
(3)
is the Riemann curvature tensor, with
(4)
By substituting (4) into (3) one finds
(5)
Here,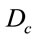 
denotes a covariant derivative with 
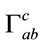as a connection and
(6)
Using in (5) the cyclic identities for 
one gets
(7)
where
(8)
Substituting (7) into (5) one obtains the key formula
(9)
For a 
-dimensional sphere 
with radius 
we have, 
,
(10)
where 
is the metric on
, and therefore one gets the expression
(11)
Contracting in (11) with 
and 
it leads to the first and the second Cartan-Shouten equations
(12)
and
(13)
respectively. Durander, Gursey and Tze [27] noted that (12) and (13) are mere covariant forms of the algebraic identities derived in normed division algebras. It turns out that (12) and (13) can be used eventually to prove that the only parallelizable spheres are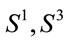 
and 
[5]. In general, however, for other 
-manifolds 
the expressions (11)-(13) do not hold.
If the only condition is that 
is parallelizable one may start with (9) instead of (11). In this case, one finds that contracting (9) with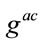 
leads to
(14)
Here, 
is the Ricci tensor.
Before we relate (14) with de Ricci flow equation used in the Poincaré conjecture let us recall how (10) is obtained. We shall focus on
, but in straightforward way one can generalize the method to any 
-sphere. Consider the line element
(15)
The sphere 
can be defined by the constraint
(16)
where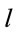 
is constant. From (16) one sees that
(17)
Rigorously, one must write
, with
. But it turns out that our computations are independent of
. Furthermore, it will be useful for further computations to write (15) and (17) in the form
(18)
and
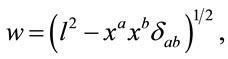(19)
respectively. The symbol 
is a Kronecker delta. From (19) one obtains
(20)
where
. So, substituting (20) into (18) yields the line element
(21)
with
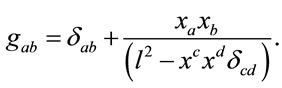(22)
The inverse 
of 
is given by
(23)
Moreover, using (22) and (23) one finds that the Christoffel symbols 
become
(24)
Considering (6), it is straightforward to see that the Riemann curvature tensor associated with (24) is given by the expression (10).
Now we would like to generalize the key constraint (19) in form
(25)
where 
is an arbitrary function of the coordinates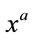
. In this case, the metric 
becomes
(26)
while the inverse 
is given by
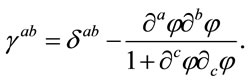(27)
The Christoffel symbols become
(28)
After lengthy but straightforward computation one discovers that the Riemann tensor 
obtained form (28) is
(29)
One can verify that when one considers the particular case
(30)
then (10) follows from (29).
Let us now consider the Ricci flow evolution equation [14] (see also Refs. [11-13] and references therein)
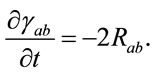(31)
Here, as before, 
is the Ricci tensor. In this case the metric 
is understood as a family of Riemann metrics on
. It has been emphasized that the Ricci flow equation is the analogue of the heat equation for metrics
. The central idea is that a metric 
associated with a closed simply connected manifold 
evolves according to (31) towards a metric 
of
. Symbolically, this means that in virtue of (31) we have the metric evolution
, which in turn must imply the homeomorphism 
.
The question arises whether one can introduce the parallelizability concept into (31). Let us assume that 
is a parallelizable manifold. We shall also assume that 
is determined by the general constraint (25). First observe that using (14), in this case the Ricci Equation (31) can be written as
(32)
This is a interesting result because it means that the evolution of 
is determined by the torsion tensor
. Moreover, combining (9) and (29) one derives the formula
(33)
which, using (26), allows to write (32) in the form
(34)
In the case of 
manifold, using (10) or (12) one obtains a Einstein type metric
(35)
and the evolution equation becomes
(36)
This type of equation is discussed extensively in references [11,13]. The relevant feature is that from the solution one sees that at large times evolution behavior of
is
, where 
corresponds to an initial condition for the metric. In this case one has 
and therefore since 
one has uniform contraction with singularity at 
(see Ref. [13] for details).
Let us now discuss some physical scenarios where the division-algebra/Poincaré-conjecture correspondence may be relevant. Let us start by first recalling the Einstein field equations with cosmological constant
,
(37)
It is known that the lowest energy solution of (37) corresponds precisely to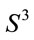 
(or to 
in general). In this case the cosmological constant 
is given by
. This can be verified using (10) and (37) (Actually this solution can be understood as a De Sitter type solution.). The question arises: how can be understood a metric solution 
of (37) associated with both 
and the Ricci flow equation? Thinking about quantum mechanics analogue one may argue that one may visualize 
as a excited state which, according to the Poincaré conjecture, must decay (homeomorphically) to
. Symbolically one may write this as
.
Considering the transition 
we discover that even in special relativity one may find this kind process. Consider the well-known time dilatation formula
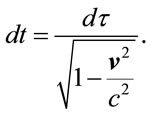(38)
Here, of course 
is the proper time, 
is the light velocity and we are thinking 
as the velocity of the relativistic object in three dimensions, namely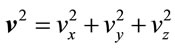 
. It is not difficult to see that (38) can also be written as
(39)
where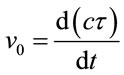
. One can understand the constraint
(39) as a formula in the space of velocities (tangent space) which determines a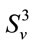 
manifold. So, one wonders what could be the corresponding generalized 3-manifold
. One may consider in an extension of (39) in the form
(40)
But in this case, the question arises whether the light velocity 
itself may be understood as excited state
. Hence, the evolution process
may be understood as the transition
. This may be relevant to consider the light velocity 
not as a given constant but as a result of evolution transition. It may be interesting to see what the torsion means in this context.
In a cosmology context we also find a possible application of the division-algebra/Poincaré-conjecture link. It is known that topologically, the standard FriedmannLemaitre-Robertson-Walker universe corresponds to a time evolving radius of a 
space. In Reference [22] it argues that if this universe is modified in
, at the end the acceleration may produce a phase transition changing 
to a space of constant curvature which corresponds precisely de Sitter phase associated with
. Another point of view is that since the Thurston three-dimensional geometrization conjecture (a generalization of the Poincaré conjecture) requires one to understand all locally homogeneous geometries on closed three manifolds, using Ricci flow one may consider Bianchi classes (see Ref. [25] for details) used to study cosmological models in a general context [28]. What one may add to this scenario is that such a transition may require a torsion in order to make 
(or other Bianchi cosmological models) parallelizable.
We would also like to describe an application of Division-algebra/Poincaré-conjecture correspondence in qubits theory. It has been mentioned in Ref. [19], and proved in Refs. [20] and [21], that for normalized qubits the complex 
-qubit, 
-qubit and 
-qubit are deeply related to division algebras via the Hopf maps, 
, 
and
, respectively. It seems that there does not exist a Hopf map for higher 
-qubit states. Therefore, from the perspective of Hopf maps, and therefore of division algebras, one arrives to the conclusion that 1-qubit, 2-qubit and 3-qubit are more special than higher dimensional qubits (see Refs. [19-21] for details). Considering the 2-qubit as a guide. One notice that 
plays the role of fiber in the map
. Thus, in principle one may think in a more general map 
in turn this may lead to a more general 2-qubit system, which one may call 2-Poinqubit (just to remember that this is a concept inspired by Poincaré conjecture). At the end one may be able to obtain the transition 2-Poinqubit®2-qubit. Of course one may extend most of the arguments developed in this work to the other Hopf maps 
and
.
Finally, it is tempting to speculate about two other topics where our formalism may have some interest. The first one refers about a possible generalization of the Ricci flow Equation (31) to a complex context. In this case the metric 
and the Ricci tensor 
may be complexified 
and
, respectively. But if this is the case then instead of (31) one must consider a Schrödinger type equation
(41)
for the evolving complex metric
. The second topic is about a possible connection of the Poincaré conjecture with oriented matroid theory [29] (see also Refs. [30-35] and references therein). This is because to any sphere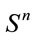 
one may associate a polyhedron which under stereographic projection corresponds to a graph in
. It turns out that matroid theory can be understood as a generalization of graph theory and therefore it may be interesting to see if there is any connection between oriented matroid theory and Poincaré conjecture. In fact in oriented matroid theory there exists the concept of pseudo-spheres which generalize the ordinary concept of spheres (see Ref. [29] for details). So one wonders whether there exists the analogue of Poincaré conjecture for pseudo-spheres.
2. Acknowledgements
I would like to thank the Mathematical, Computational & Modeling Science Center of the Arizona State University where part of this work was developed. This work was partially supported by Profapi/2012.