Delay-Dependent Robust Passive Control for Uncertain Discrete-Time Systems with Time Delays ()
1. Introduction
In the past several years, much attention has been paid to the study of stability of systems with control input delay. Much of them is focused on the passivity analysis for classes of time-delay systems. Using classical definitions of passivity and positive realness, the conditions for a nonlinear system can be rendered passive via smooth state feedback, see [1,2]. The robust passive control problem for time-delay systems was dealt with in [3,4] via various approaches. The robust passivity synthesis problem for discrete-time-delay systems is investigated in [5,6], but all these time delays are constant. To the best knowledge of authors, the problem of robust passive control for discrete-time systems with time-varying delays has not been fully investigated, which is more complex.
In this paper, we deal with the problem of robust passive feedback control for discrete systems with parameter uncertainties and time-varying delays. The parameter uncertainties are assumed to be time-varying but normbounded. The purpose is to construct a state feedback controller such that the closed-loop system is strictly passive and obtain a delay-dependent condition for the solvability of the problem.
2. Statement of the Problem
Consider the following uncertain discrete-time system with time-varying delays:
(2.1)
(2.2)
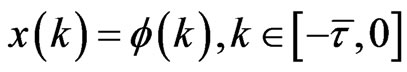(2.3)
where 
is the state, 
is the controlled output,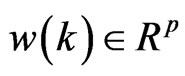 
the disturbance input which is assumed to belong to
; 
is a positive integer representing the time-varying delay of the system, which satisfies the following assumption:
. 
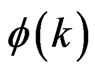is a real-valued initial function on
; 
and 
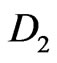are known real constant matrices; 
and 
are unknown matrices representing time-varying parameter uncertainties, and are assumed to be of the form
(2.4)
where 
and
, are known real constant matrices and 
satisfies:
. (2.5)
Our problem is to establish the passive control for systems (2.1)-(2.3) to determine the conditions. To this end, we introduce the following fact and related definition of passivity.
Lemma 2.1 Given constant symmetric matrices
, 
, 
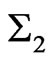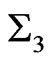, where
, and
, then
if and only if
.
Lemma 2.2 Given constant matrices
, 
, 
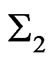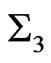of appropriate dimensions with
. Then
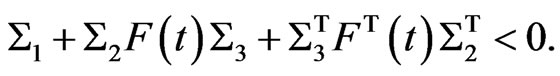
where 
if and only if for some scalar 
Lemma 2.3 Let
, then the following inequality holds for any matrices R, S1, 
and positive scalar
:
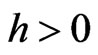Definition 2.1 The dynamical systems (2.1) - (2.3) is called passive if there exists a scalar 
such that
where 
is some constant which depends on the initial condition of the system.
In addition, the systems (2.1)-(2.3) is said to be strictly passive if it is passive and
. In the sequel, we provide conditions under which a class of discretetime linear dynamical systems with time-varying parameter uncertainties can be guaranteed to be strictly passive. First, we have the following result pertaining to the system (2.1)-(2.3).
3. Proof of Main Results
Theorem 3.1 The discrete-time systems with time delay (2.3) is strictly passive if there exist symmetric positive definite matrices P, R, Q and
, such that the following LMI holds:
(3.1)
where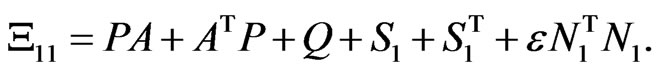 
Proof. Choose a Lyapunov function candidate for the system (2.1) - (2.3) as follows:
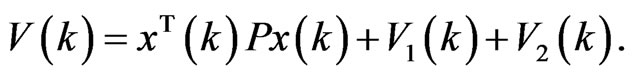(3.2)
where
Now, by some calculations, we can get that
(3.3)
We define that
, then have
. (3.4)
From the Lemma 2.3, for
, we can have that
(3.5)
We have (3.3) and (3.4) into (3.2), after some manipulation, then obtain the following inequality:
(3.6)
where
.
If
, then
, and from which it follows that
. (3.7)
Since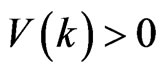 
for 
and 
for x = 0, it follow as
, that systems (2.1) - (2.3) is strictly passive. In view of Definition 2.1, the strictly passive condition is guaranteed if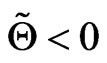 
and it can be expressed conveniently as
(3.8)
where
.
Application of Lemma 2.1 to the above inequality, it puts into the following form:
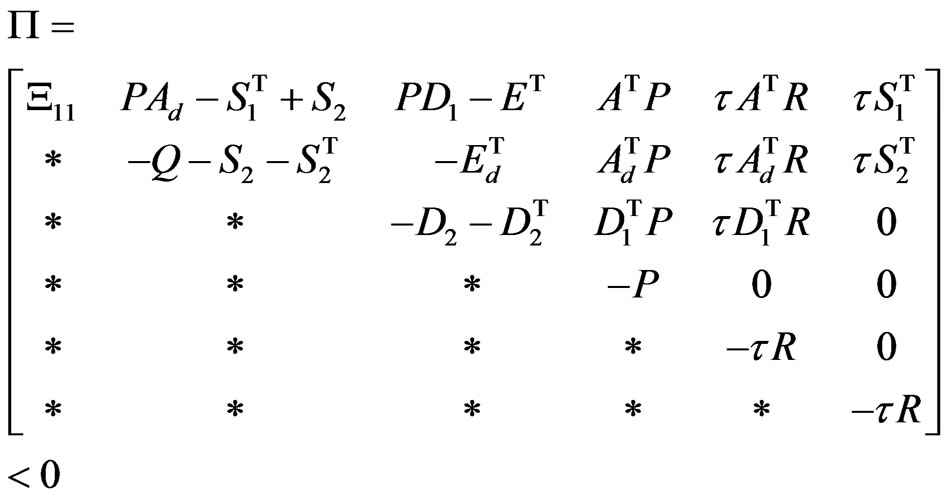
(3.9)
Substituting the uncertainty structure (2.5) into (3.9) and rearranging, we get the following inequality
(3.10)
Then by Lemma 2.2, the inequality (3.10) holds if and only if for some 
(3.11)
for all admissible uncertainties satisfying (2.4). On using Lemma 2.1 in (3.11), it becomes that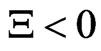 
in (3.1). This completes the proof.
4. Robust Passive State Feedback Controller
We now build on the foregoing results by considering the passive control problem, that is, designing a state feedback controller to render the closed-loop time-delay system passive. Extending the system (2.1)-(2.3), we consider a class of time-delay systems of the form:
(4.1)
(4.2)
where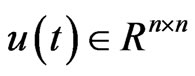 
is the control input, 
, 
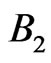, are known real constant matrices; 
and 
are unknown matrices representing time-varying parametre uncertainties, and are assumed to be of the form:
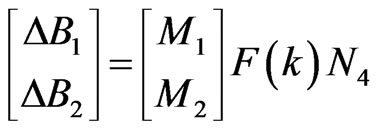. (4.3)
Then the transformed system becomes
(4.4)
(4.5)
then we observe that
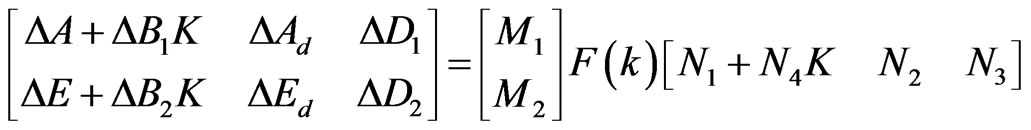. (4.6)
The following theorem establishes the main result.
Theorem 4.1 Consider the uncertain discrete-time delay system (4.4), (4.5). If there exists a positive scalar
, a real matrix Y, three symmetric positive definite matrices
, 
, 
such that the following inequality holds:
(4.7)
where
then the systems (4.4), (4.5) are strictly passive, and the state-feedback gain matrix is given by
.
Proof. Similar to Theorem 3.1.
Remark 4.1 It is noted that the matrix inequalities conditions in Theorem 4.1 are not LMIs. In order to solve the matrix inequalities conditions in Theorem 4.1, we can follow a similar line as in Lee et al. (2004) and Moon et al. (2001) to provide a nonlinear minimization problem subject to LMIs.
NOTES