1. Introduction
It is a well-known fact that variable transformations are valuable in considering the effect of tax and transfer policies on income inequality. The transformation is usually assumed to be positive, monotone increasing and continuous. Under the assumption that the theorems should hold for all income distributions, conditions given earlier are both necessary and sufficient [1,2]. In this study, we reconsider the effect of variable transformations on the redistribution of income. Different versions of the conditions are compared [1,3-5]. One main result is that continuity is a necessary condition if one assumes that income inequality should remain or be reduced. In addition, in our earlier studies of classes of tax policies, the results were based on the assumption that the transformations were differentiable and satisfies a derivative condition [6,7].
2. Basic Properties of Income Transformations
Consider income X with the distribution function , the mean
, the mean , and the Lorenz curve
, and the Lorenz curve . We assume that X is defined for
. We assume that X is defined for  and that
and that  is continuous.
is continuous.
A fundamental theorem concerning the effect of income transformations on Lorenz curves and Lorenz dominance was given by Fellman [3] and Jakobsson [1] and later by Kakwani [4]. We have.
Theorem 1. [1,3,4]. Let X be an arbitrary non-negative, random variable with the distribution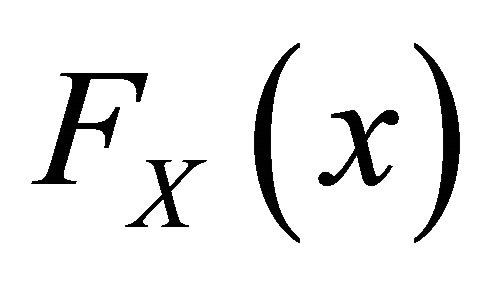 , mean
, mean , and Lorenz curve
, and Lorenz curve . Let
. Let  be nonnegative, continuous and monotone-increasing and let
be nonnegative, continuous and monotone-increasing and let  exist. Then the Lorenz curve
exist. Then the Lorenz curve  of
of  exists and the following results hold 1)
exists and the following results hold 1) 
if  is monotone decreasing;
is monotone decreasing;
2) 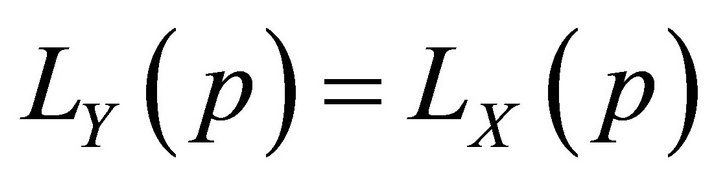
if  is constant and;
is constant and;
3) 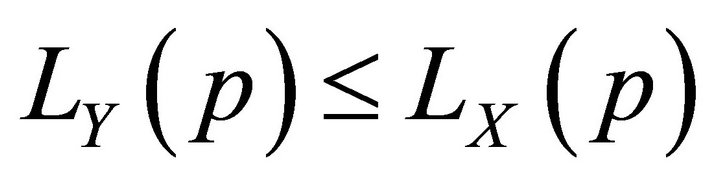
if  is monotone increasing.
is monotone increasing.
Following Fellman [2], we obtain in 1) a sufficient condition that the transformation  generates a new income distribution which Lorenz dominates the initial one. The analysis should be based on the difference
generates a new income distribution which Lorenz dominates the initial one. The analysis should be based on the difference
 (1)
(1)
where  ; that is,
; that is, 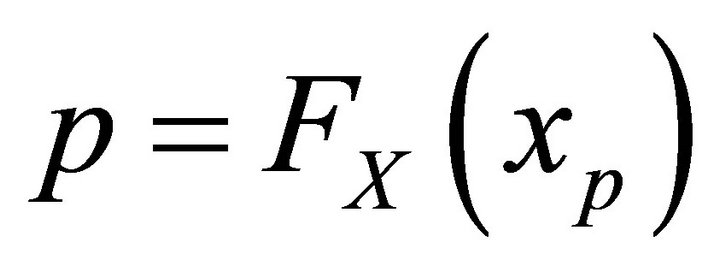 [2]. Furthermore,
[2]. Furthermore, . In order to obtain Lorenz dominance, the difference
. In order to obtain Lorenz dominance, the difference 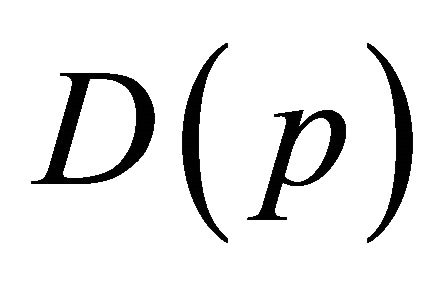 in Equation (1) must start from zero, attain positive values and then decrease back to zero. Consequently, the difference
in Equation (1) must start from zero, attain positive values and then decrease back to zero. Consequently, the difference
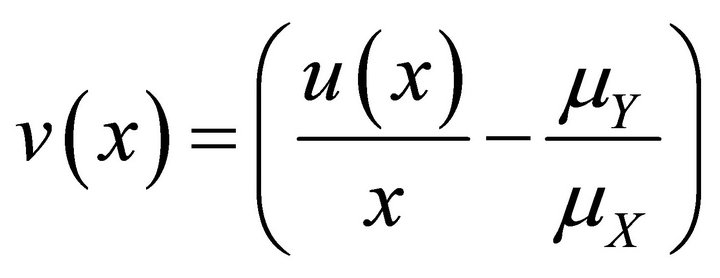 (2)
(2)
must start from positive (non-negative) values and then change its sign and become negative. If  is exceptionally increasing within the interval
is exceptionally increasing within the interval , then a variable X with a distribution
, then a variable X with a distribution  defined in the interval
defined in the interval  exists such that 3) holds and
exists such that 3) holds and  . Consequently, the condition that
. Consequently, the condition that 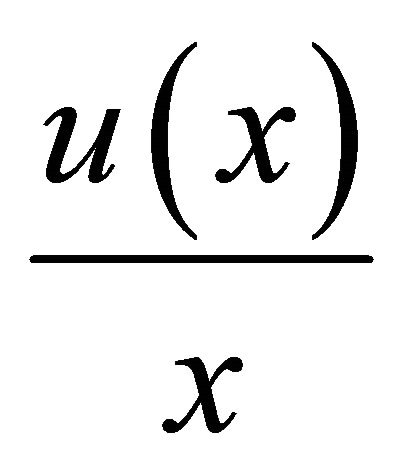 is decreasing is necessary if the rule holds for all income distributions
is decreasing is necessary if the rule holds for all income distributions  [1,2]. Analogously, if the other results in Theorem 1 hold for every income distribution, the conditions in 2) and 3) are also necessary.
[1,2]. Analogously, if the other results in Theorem 1 hold for every income distribution, the conditions in 2) and 3) are also necessary.
Hence, the continuity of  is a necessary condition if we demand that the transformed variable should Lorenz dominate the initial variable for every distribution. From this it follows that if the condition in Theorem 1 1) has to be necessary, it implies continuity and hence an explicit statement of continuity can be dropped. Considering the condition in 2), we observe that
is a necessary condition if we demand that the transformed variable should Lorenz dominate the initial variable for every distribution. From this it follows that if the condition in Theorem 1 1) has to be necessary, it implies continuity and hence an explicit statement of continuity can be dropped. Considering the condition in 2), we observe that  and
and  consequently is continuous.
consequently is continuous.
However, in case 3) discontinuities do not jeopardize the monotone increasing property of the quotient 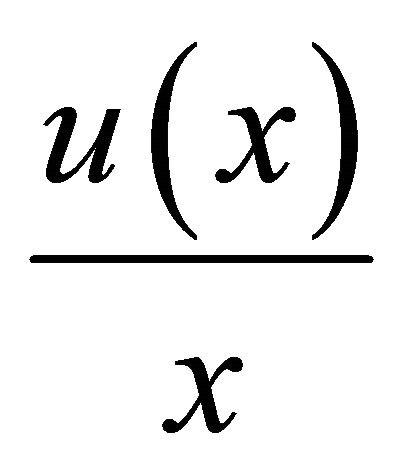 and the result in Theorem 1 3) holds even if the function is discontinuous. Therefore, Fellman [2] dropped the explicit continuity assumption in this case as well.
and the result in Theorem 1 3) holds even if the function is discontinuous. Therefore, Fellman [2] dropped the explicit continuity assumption in this case as well.
Summing up, for arbitrary distributions,  , the conditions 1), 2), and 3) in Theorem 1 are both necessary and sufficient for the dominance relations and an additional assumption about the continuity of the transformation
, the conditions 1), 2), and 3) in Theorem 1 are both necessary and sufficient for the dominance relations and an additional assumption about the continuity of the transformation  can be dropped. We obtain the more general theorem [2].
can be dropped. We obtain the more general theorem [2].
Theorem 2. Let X be an arbitrary non-negative, random variable with the distribution  , mean
, mean  and Lorenz curve
and Lorenz curve 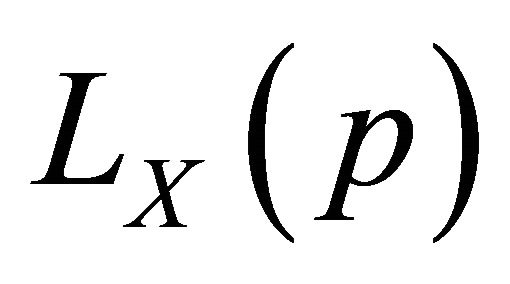 , let
, let  be a non-negative, monotone increasing function and let
be a non-negative, monotone increasing function and let  and
and  exist. Then the Lorenz curve
exist. Then the Lorenz curve 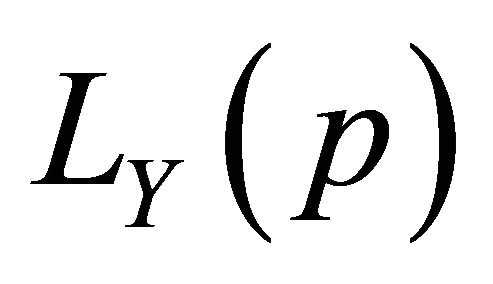 of Y exists and the following results hold:
of Y exists and the following results hold:
1) 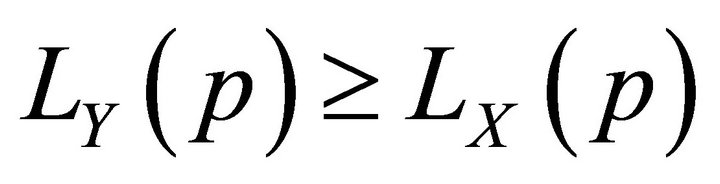
if and only if  is monotone-decreasing 2)
is monotone-decreasing 2) 
if and only if 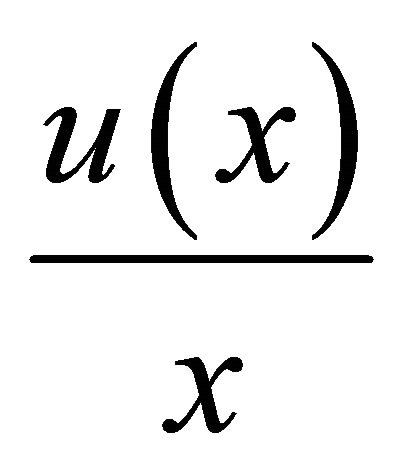 is constant 3)
is constant 3) 
if and only if  is monotone-increasing.
is monotone-increasing.
Remark. It follows from the discussion above that the transformation  can be discontinuous only in case 3).
can be discontinuous only in case 3).
Hemming and Keen [5] gave an alternative condition for Lorenz dominance. Their condition, with our notations, is that for a given distribution ,
,  crosses the
crosses the  level once from above. Consequently,
level once from above. Consequently,  in (2) starts from positive valueschanges its sign once and ends up with negative values. Hence, their condition is equivalent to our condition.
in (2) starts from positive valueschanges its sign once and ends up with negative values. Hence, their condition is equivalent to our condition.
Furthermore, if we assume that  is monotonedecreasing (non-increasing), then
is monotonedecreasing (non-increasing), then  satisfies the condition “crossing once from above for every distribution
satisfies the condition “crossing once from above for every distribution ”. Hence, both conditions, the HemmingKeen condition and ours, are also equivalent as necessary conditions. Recently, Fellman [8] obtained limits for the transformed Lorenz curves. These limits are related to the results given by Hemming and Keen.
”. Hence, both conditions, the HemmingKeen condition and ours, are also equivalent as necessary conditions. Recently, Fellman [8] obtained limits for the transformed Lorenz curves. These limits are related to the results given by Hemming and Keen.
3. Properties of Tax Policies
If we apply the results above to tax policies, the transformed variable  is the income after the taxation (cf., e.g., [6,7,9,10]). In order to obtain a realistic class of policies, Fellman [6,7] assumed continuous transformations and included the additional restriction
is the income after the taxation (cf., e.g., [6,7,9,10]). In order to obtain a realistic class of policies, Fellman [6,7] assumed continuous transformations and included the additional restriction . This condition indicates that the tax paid is an increasing function of the income x. In order to generalize the results and allow that the function
. This condition indicates that the tax paid is an increasing function of the income x. In order to generalize the results and allow that the function  is not uniformly differentiable everywhere, we replace the derivative restriction in this study by the more general condition
is not uniformly differentiable everywhere, we replace the derivative restriction in this study by the more general condition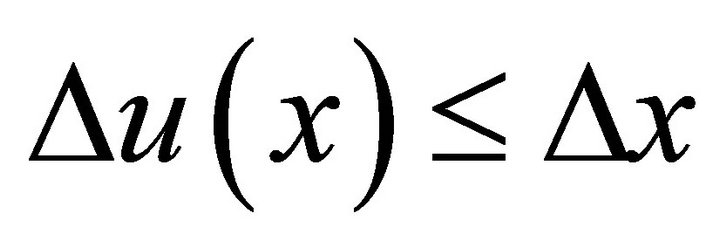 . According to this restriction, the tax is an increasing function of the income x. In fact, the tax is
. According to this restriction, the tax is an increasing function of the income x. In fact, the tax is 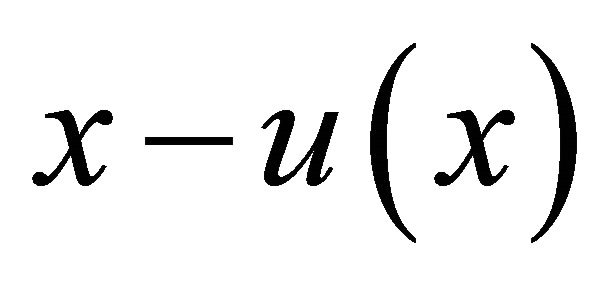 and the increment in the tax is
and the increment in the tax is  and a positive increment
and a positive increment 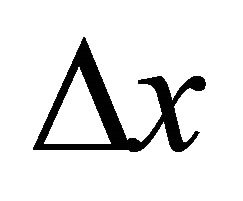 yields the restriction
yields the restriction . If
. If  holds, it follows that
holds, it follows that
 (3)
(3)
but the condition  is more general and does not imply uniform differentiability. Both restrictions imply that the transformation
is more general and does not imply uniform differentiability. Both restrictions imply that the transformation 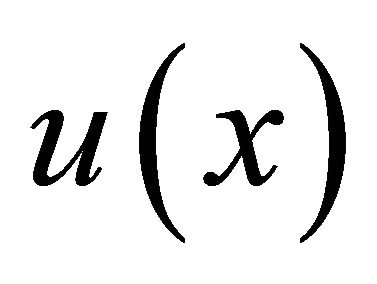 is continuous. We intend to show that the assumption
is continuous. We intend to show that the assumption  is sufficient for the whole theory.
is sufficient for the whole theory.
Now, the class of tax policies is U: (4)
(4)
We consider the extreme policies
 (5)
(5)
and
 (6)
(6)
It is apparent that while function (5) is not differentiable at point  and (6) at point
and (6) at point , the condition
, the condition  holds for all x. The Lorenz curve corresponding to (5) is
holds for all x. The Lorenz curve corresponding to (5) is
 (7)
(7)
where  and the Lorenz curve corresponding to (6) is
and the Lorenz curve corresponding to (6) is
 (8)
(8)
where  ([6]).
([6]).
Policy (5) is optimal, that is, it Lorenz dominates all the policies in class U, and policy (6) is Lorenz dominated by all policies in U [6,7].
In the following, we show how the main result in [7] can be obtained when we replace the restriction  by the more general restriction
by the more general restriction . The function
. The function  may be piecewise differentiable like transformations (5) and (6). We consider post-tax income distributions with the mean
may be piecewise differentiable like transformations (5) and (6). We consider post-tax income distributions with the mean . Without the restriction
. Without the restriction , the necessary and sufficient condition that a given Lorenz curve
, the necessary and sufficient condition that a given Lorenz curve  of the distribution
of the distribution  corresponds to a member of class U is that the initial distribution
corresponds to a member of class U is that the initial distribution  stochastically dominates
stochastically dominates . The inclusion of the restriction
. The inclusion of the restriction  results in the stochastic dominance being only necessary; that is, the transformed distribution
results in the stochastic dominance being only necessary; that is, the transformed distribution 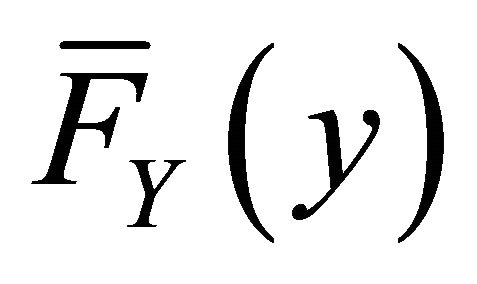 must satisfy additional conditions.
must satisfy additional conditions.
Assume a given differentiable Lorenz curve  with a continuous derivative. These conditions can be assumed because the corresponding transformation
with a continuous derivative. These conditions can be assumed because the corresponding transformation  has to continuously satisfy the condition
has to continuously satisfy the condition . Starting from
. Starting from , the connection between
, the connection between 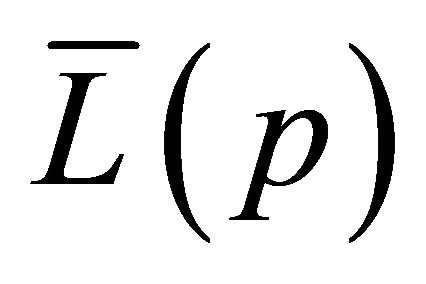 and the post-tax distribution
and the post-tax distribution  with the mean
with the mean  is that
is that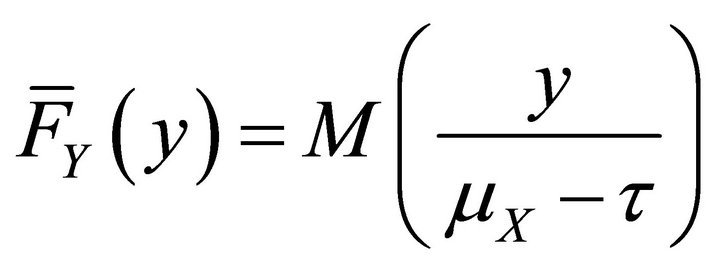 , where
, where  is the inverse function of
is the inverse function of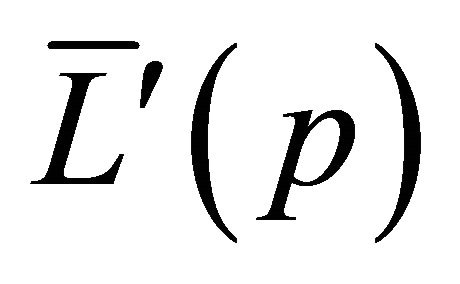 . The corresponding transformation is
. The corresponding transformation is 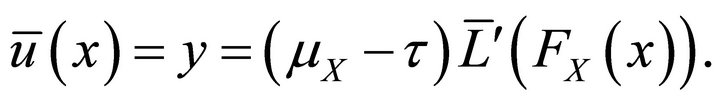
The condition  can be written as
can be written as
 (9)
(9)
where  and
and 
On the other hand, we can write
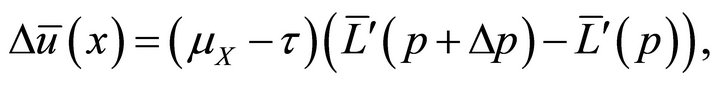 (10)
(10)
and define  and
and 
 .
.
If we assume that  is piecewise differentiable, then
is piecewise differentiable, then  and
and 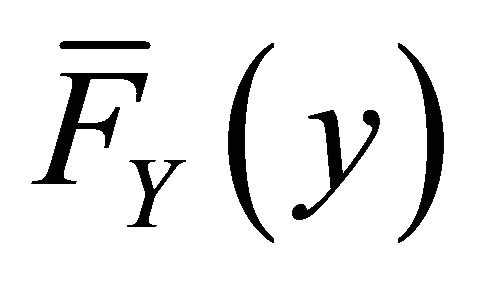 are piecewise differentiable.
are piecewise differentiable.
If we assume that the density functions  and
and  exist, we obtain
exist, we obtain
 (11)
(11)
where  and
and
 (12)
(12)
where  and
and .
.
Consequently,  and
and 
From  and from the condition
and from the condition  it follows that
it follows that
 (13)
(13)
and, consequently,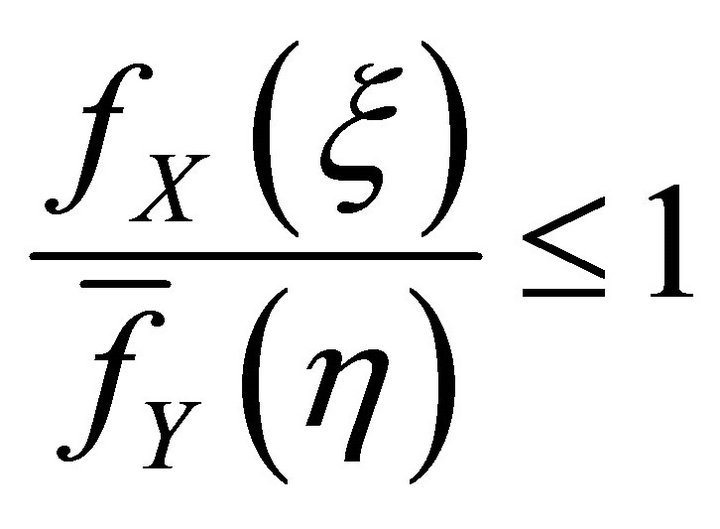 . If we let
. If we let , then
, then 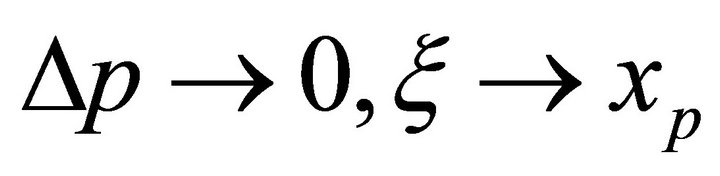 and
and  and we obtain
and we obtain  for all p. This condition can also be written as
for all p. This condition can also be written as 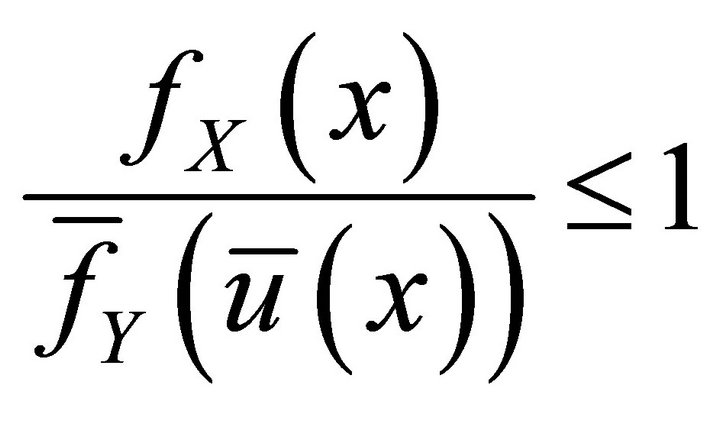 or
or 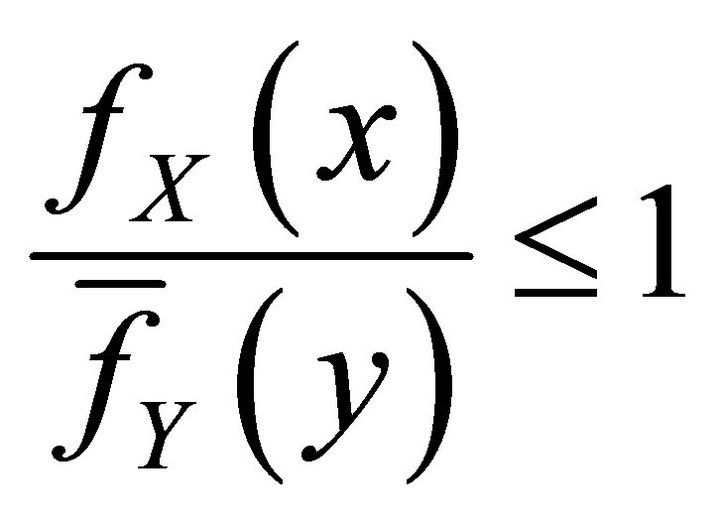 (14)
(14)
when . We can reverse the steps from (14) to (9) and all the results in Fellman [7] still hold, but the proof had to be slightly modified.
. We can reverse the steps from (14) to (9) and all the results in Fellman [7] still hold, but the proof had to be slightly modified.
4. Conclusions
In this study we reconsidered the effect of variable transformations on the redistribution of income. The aim was to generalise the conditions considered in earlier papers. We were particularly interested in whether we could drop the assumption of differentiability of the transformations when tax policies are considered. The main result is that with a slight modification of the proof the additional condition  is obtained.
is obtained.
We have also seen that if we demand sufficient and necessary conditions, theorems obtained earlier still hold and the continuity assumption can be included in the general conditions. The main result is that continuity is a necessary condition if one maintains that the income inequality should remain or be reduced.
The study of the class of tax policies indicated that the differentiability assumed earlier, can be dropped but, if one wants to retain the realism of the class, the transformations should still be continuous and satisfy the restriction . The previous results in Fellman [6,7] still hold.
. The previous results in Fellman [6,7] still hold.
Empirical applications of the optimal policies of a class of transfer policies and the class of tax policies considered here have been discussed by Fellman et al. [9,10], where “optimal yardsticks” to gauge the effectiveness of given real tax and transfer policies in reducing inequality were developed.