A New Algorithm for Computing the Determinant and the Inverse of a Pentadiagonal Toeplitz Matrix ()
1. Introduction
Pentadiagonal Toeplitz matrix linear systems often occur in several fields such as numerical solution of differential equations, interpolation problems, boundary value problems [1-5], etc. In these areas, the determinants and the inversions of pentadiagonal Toeplitz matrices are considered. In recent years they have become one of the most important and active research field of applied mathematics and computational mathematics increasingly.
In [2], E. Kilic, M. Ei-Mikkawy presented a fast and reliable algorithm with the cost of 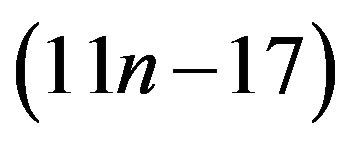 for evaluating special nth-order pentadiagonal Toeplitz determinants. In [1], X.G. Lv, T.Z. Huang, J. Le presented an algorithm with the cost of
for evaluating special nth-order pentadiagonal Toeplitz determinants. In [1], X.G. Lv, T.Z. Huang, J. Le presented an algorithm with the cost of  for calculating the determinant of a pentadiagonal Toeplitz matrix and an algorithm for calculating the inverse of a pentadiagonal Toeplitz matrix.
for calculating the determinant of a pentadiagonal Toeplitz matrix and an algorithm for calculating the inverse of a pentadiagonal Toeplitz matrix.
In this paper, we present new algorithms for computing the determinant and the inverse of an n-by-n pentadiagonal Toeplitz matrix. The complexity of the algorithms are 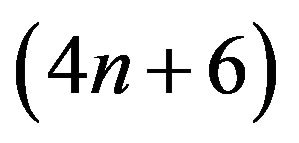 and
and 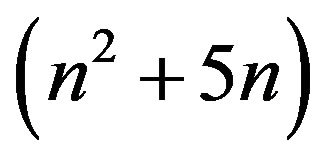 respectively.
respectively.
This paper is organized as follows: in Section 2, we present some useful notations and lemmas. In Section 3, we are going to derive new two algorithms. Finally, we give an numerical examples to show the performance of our algorithms in Section 4.
2. Notations and Preliminaries
Definition 2.1 Let 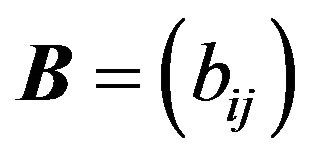 be an
be an 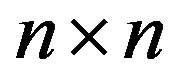 matrix.
matrix. 
is called persymmetric if it symmetric about its northeast-southwest diagonal, i.e.,  for all
for all 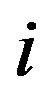 and
and .
.
Definition 2.2 Form as
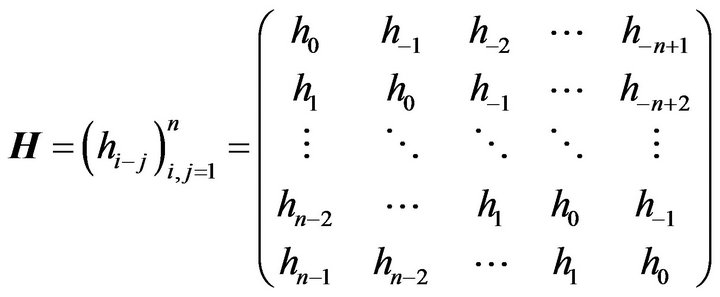
is called Toeplitz matrix.
Toeplitz matrices are all persymmetric matrices.
Lemma 2.1 [6] Let  be an
be an 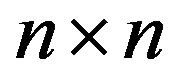 matrix. Then
matrix. Then
(1)  is persymmetric matrix if and only if
is persymmetric matrix if and only if 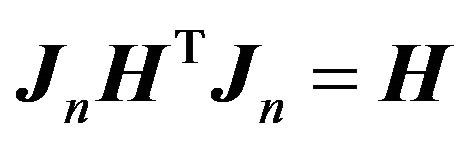 ;
;
(2) If  is nonsingular Toeplitz matrix,
is nonsingular Toeplitz matrix, 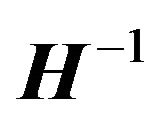 is also a Toeplitz matrix, where
is also a Toeplitz matrix, where  is the
is the 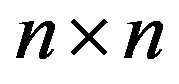 exchange matrix, i.e.,
exchange matrix, i.e.,  ,
,  is the ith column of identity matrix
is the ith column of identity matrix 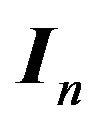 of order
of order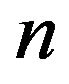 .
.
Without loss of generality, we suppose 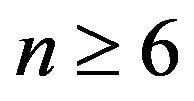 in the paper. By computing simply, we have the following conclusion:
in the paper. By computing simply, we have the following conclusion:
Lemma 2.2 Let 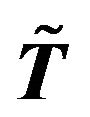 be an
be an 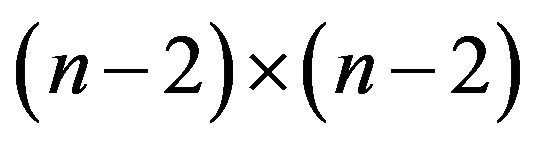 Toeplitz matrix
Toeplitz matrix
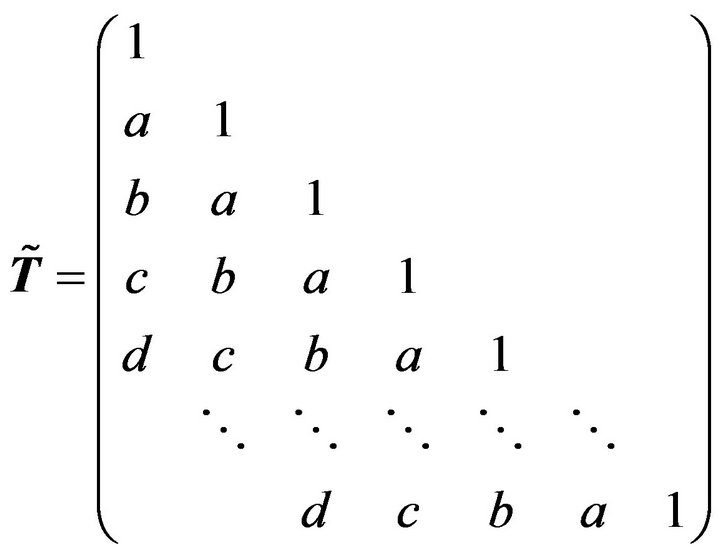 (2.1)
(2.1)
Then the inverse of 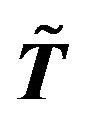 is an
is an 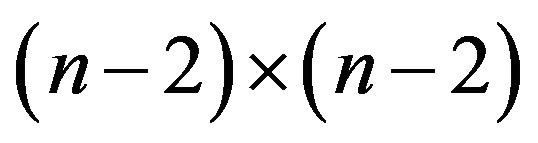 Toeplitz matrix, and
Toeplitz matrix, and

where
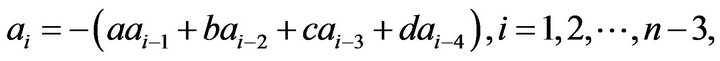
and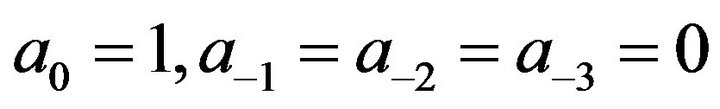 .
.
Lemma 2.3 Let 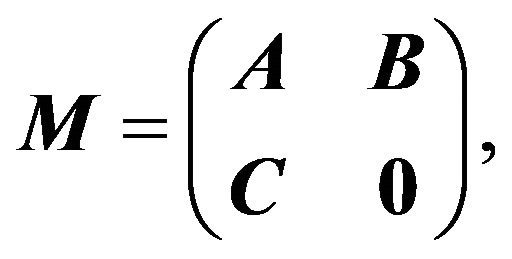 where
where 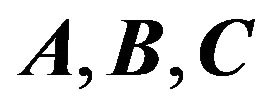 and
and
 are matrices of size
are matrices of size
 respectively.
respectively.  is nonsingular. Then
is nonsingular. Then 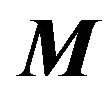 is nonsingular if and only if
is nonsingular if and only if 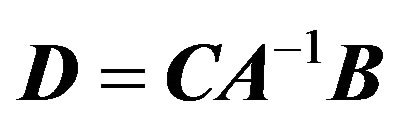 is nonsingular, and
is nonsingular, and
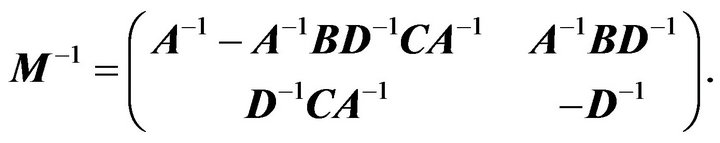
In the current paper, we consider the  pentadiagonal Toeplitz matrix of the form
pentadiagonal Toeplitz matrix of the form
 (2.2)
(2.2)
3. Main Results
Decompose the pentadiagonal Toeplitz matrix  (2.2) as the following:
(2.2) as the following:
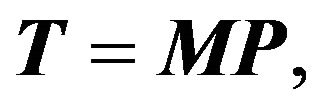
where

Partition M into 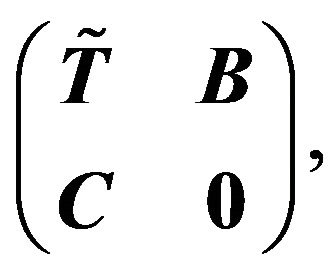 where
where 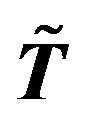 is matrix (2.1),
is matrix (2.1),
 is zero matrix of size
is zero matrix of size ,
,
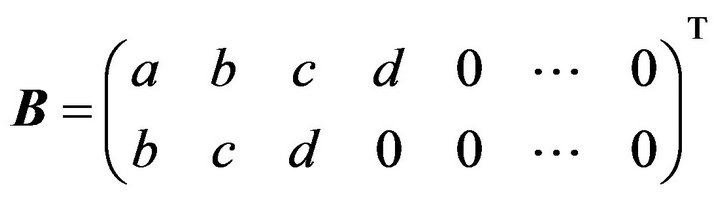 of size
of size 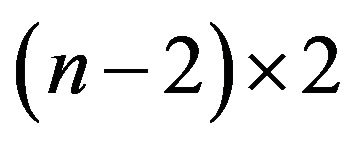 and
and
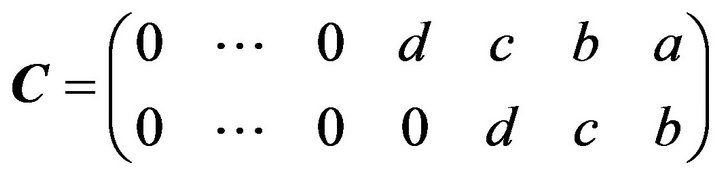 of size
of size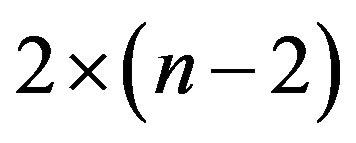 .
.
Thus

where
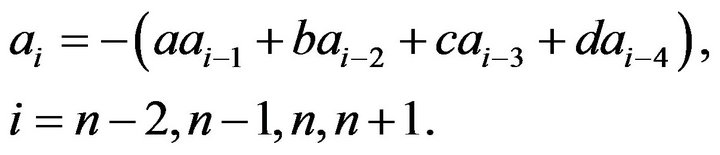
Denote
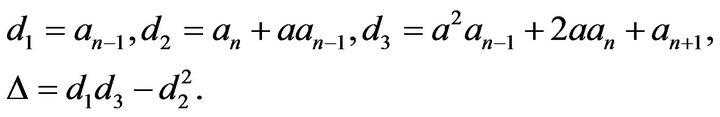
Thus

It is noticed that
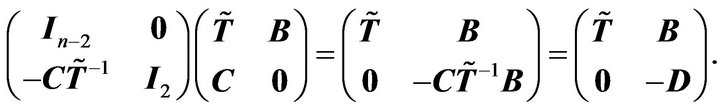
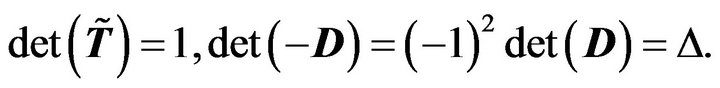
We have
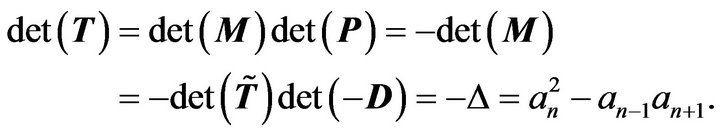
According to the Lemma 2.3 and deduction above, we have the following results:
Theorem 3.1 Let  be the pentadiagonal Toeplitz matrix as (2.2), then (1)
be the pentadiagonal Toeplitz matrix as (2.2), then (1)  is nonsingular if and only if
is nonsingular if and only if 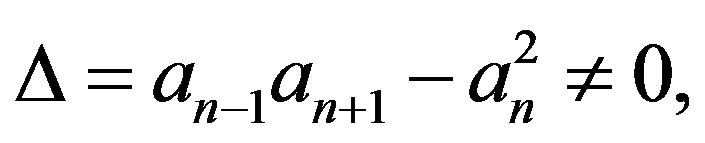 and
and
(2) 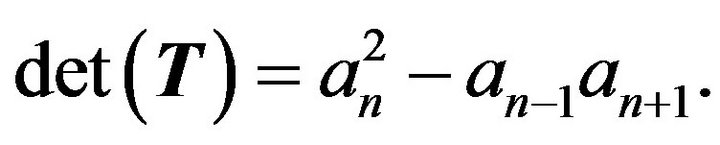
When 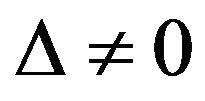 , we have that
, we have that  is nonsingular, and
is nonsingular, and
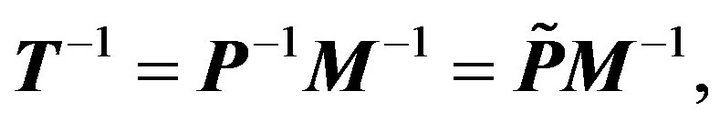
where

and 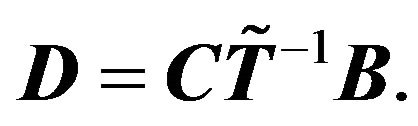
Denote 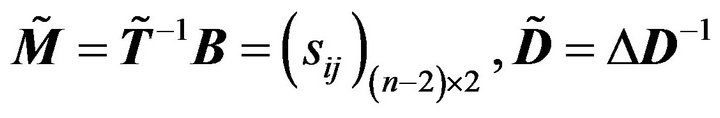 and
and
 We have
We have

i.e.,
 (3.2)
(3.2)
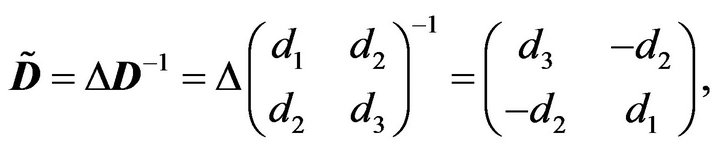

i.e.,
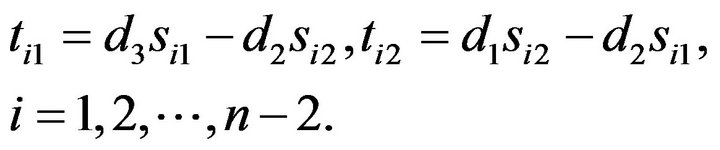 (3.4)
(3.4)
From the Lemma 2.1 and 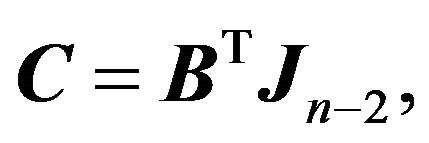 we have
we have
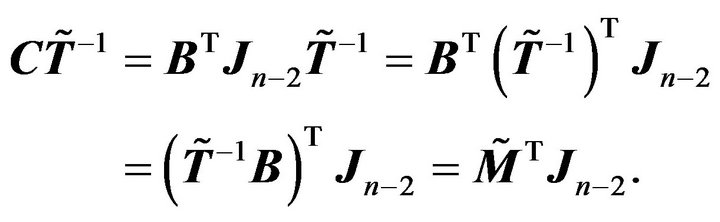
Thus
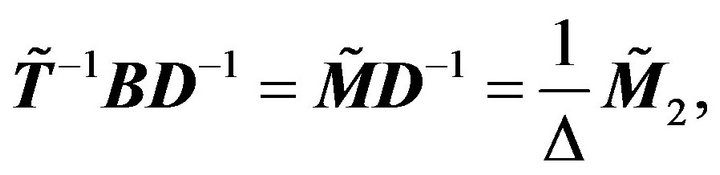

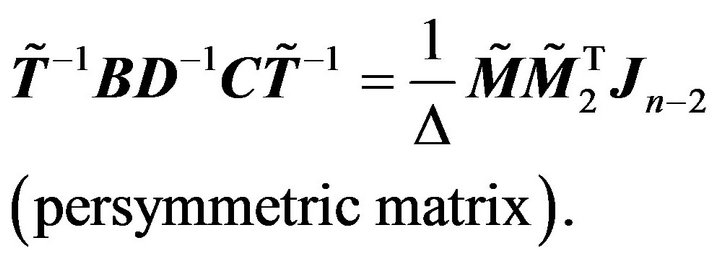
Denote
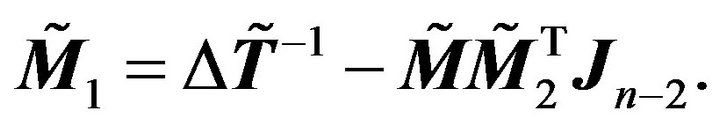 (3.5)
(3.5)
Then 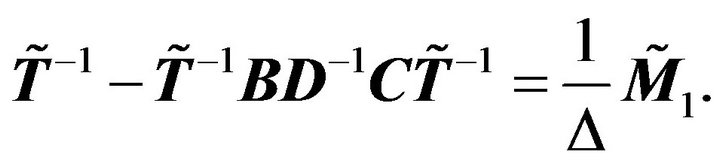
According to the deduction above, we can obtain Theorem 3.2:
Theorem 3.2 Let the pentadiagonal Toeplitz matrix  as (2.2) be nonsingular. Then
as (2.2) be nonsingular. Then
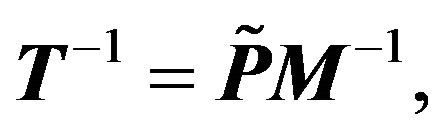
where

 as above.
as above.
Combining with Theorem 3.1 and Theorem 3.2, we obtain the following algorithm:
Algorithm 3.1 (Computing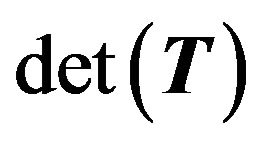 )
)
(1) Input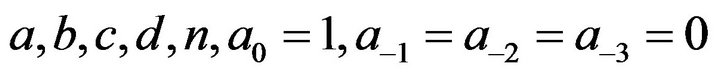 ;
;
(2) Compute
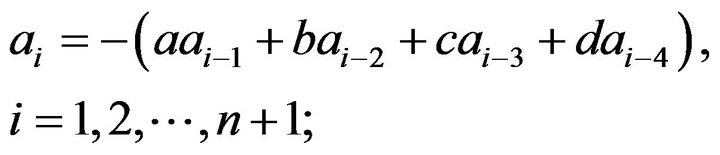
(3) Compute 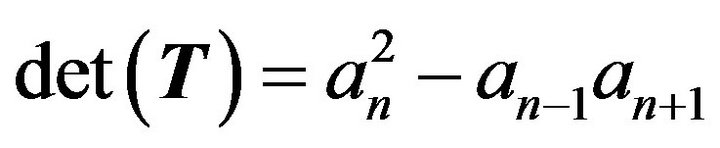 .
.
Algorithm 3.2 (Computing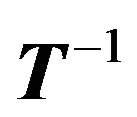 )
)
(1) Using (3.1), calculate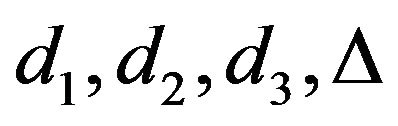 ;
;
(2) Using (3.2), calculate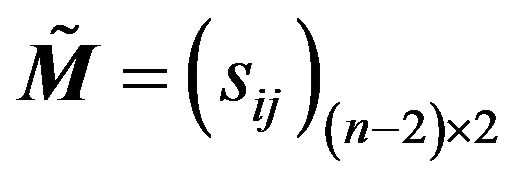 ;
;
(3) Using (3.4), calculate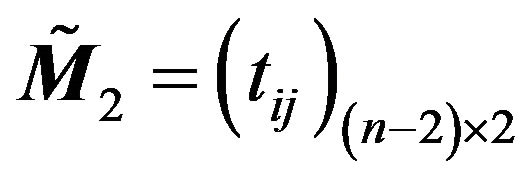 ;
;
(4) Using (3.3) and (3.5), calculate ;
;
(5) Calculate ;
;
(6) Calculate .
.
Let us now have a look at the number of multiplications and divisions executed by Algorithm 3.1 and 3.2. For Algorithm 3.1, in Step 2, it takes about 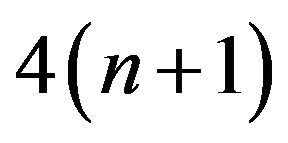 operations. Step 3 amounts to 2 operations. On the whole, we need about
operations. Step 3 amounts to 2 operations. On the whole, we need about 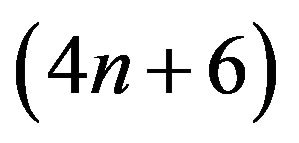 operations to compute
operations to compute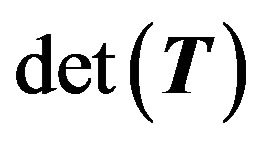 . Algorithm 3.1 is better than E. Killic’s algorithm [2] with the cost of
. Algorithm 3.1 is better than E. Killic’s algorithm [2] with the cost of  and X.G. Lv’s algorithm [1] with the cost of
and X.G. Lv’s algorithm [1] with the cost of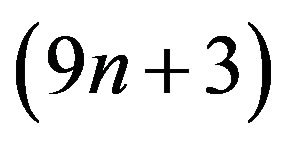 . For Algorithm 3.2, in Step 1, it takes 4 operations. Step 2 amounts to
. For Algorithm 3.2, in Step 1, it takes 4 operations. Step 2 amounts to 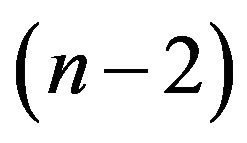 operations. Step 3 amounts to
operations. Step 3 amounts to 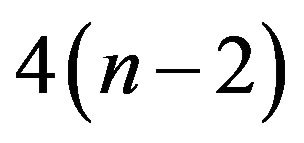 operations. The cost of step 4 is about
operations. The cost of step 4 is about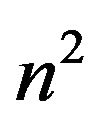 , we make use of the persymmetric matrix. Therefore, we need about
, we make use of the persymmetric matrix. Therefore, we need about 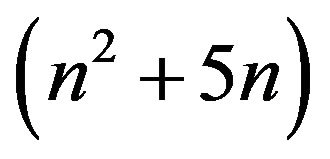 operations computing
operations computing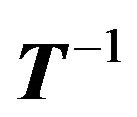 . Our algorithm is better than X.G. Lv’s algorithm [1] with the cost of
. Our algorithm is better than X.G. Lv’s algorithm [1] with the cost of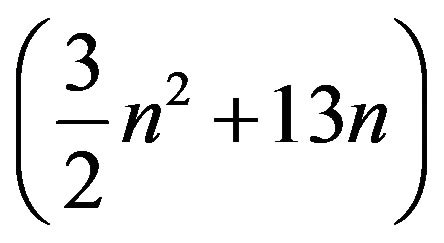 .
.
4. An Example
Consider the pentadiagonal Toeplitz matrix as

By Algorithm 3.1, we have
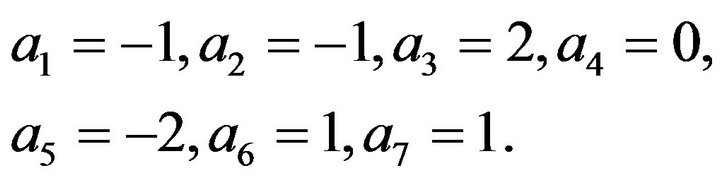
So
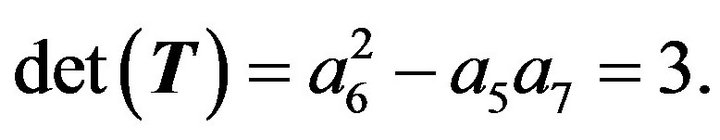
Using Algorithm 3.2, we obtain
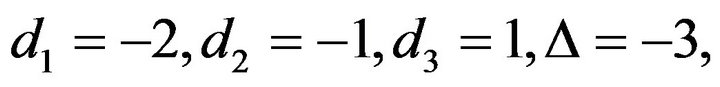
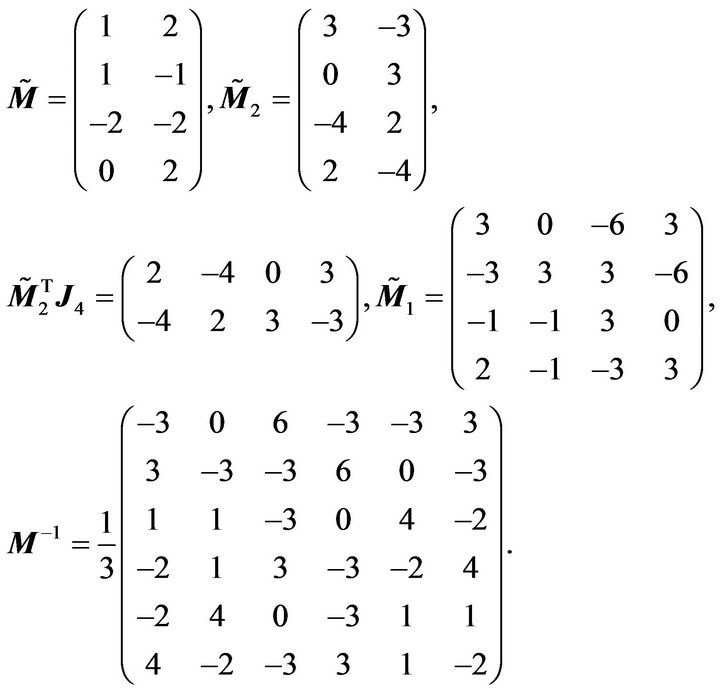
So

NOTES