New Generating Sets of the First Order Lane-Emden Differential Equations in N-Dimensional Radially Symmetric Polytropes ()
1. Introduction
The reduction of the differential equations is probably the most challenging problem in dynamics and physics. A general interpretation of reducibility includes various transformations and changes the original problem not only along mathematical lines but also in a physical sense. Such transformations will be achieved using homology theorem.
Homology is a powerful tool used by mathematicians to study the properties of spaces and maps that are insensitive to small perturbations. It was first used in a topological sense by Henri Poincaré (1895) as a relation between manifolds mapped into a manifold. The homology group was further developed for computational purposes by several investigators [1-3]. Kaczynski et al. [4] presented the conceptual background for computational homology and indicated how homology can be used to study nonlinear dynamics.
The important consequence of the use of homology theorem, is that, if we can find two independent homology invariant functions, say u and v, then the Lane-Emden equation transformed to u and v variables is of order one. Moreover, homology invariant functions play important role in fitting up solutions at the surface of the composite stellar models [5].
In the present paper, two new generating sets, of homology invariant functions will be established. Moreover, by the aid of two independent homology invariant functions of each set we established the transformed first order Lane-Emden equation. The first equation for polytropic index 
depends on five free parameters, while, the other equation is for, 
and depends on three free parameters.
2. Lane-Emden Differential Equations
The basic equations for N-dimensional radially symmetric polytropes are the generalized Lane-Emden differential equations depending on the geometric index N, such that, N = 1 (slab), N = 2 (cylinder) and N = 3 (sphere), and the polytropic index n. These equations are given as [6]
(1)
(2)
where 
; 
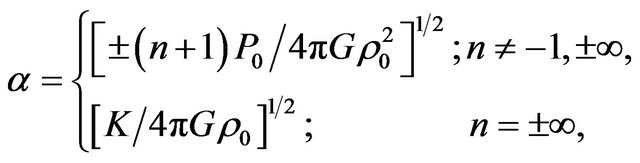
and 
The upper sign corresponds to values of polytropic index
, the lower one to
. The special case n = −1 appears as limiting case of two polytropic sequences having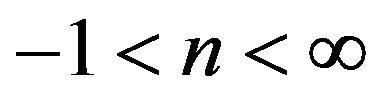 
and
, respectively. Also, r is the radial distance, 
are the Lane-Emden variables, K is the Boltzmann constant and G is the gravitational constant. The initial conditions of Equations (1) and (2) are;
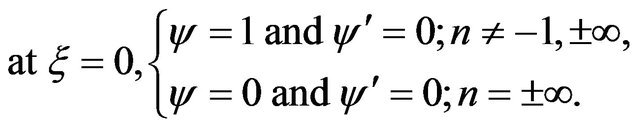(3)
If these conditions are satisfied then 
and 
are just equal to the pressure and density at radial distance 
3. The Homology Theorem and Homology Invariant Functions
3.1. Theorem
If 
is a solution of the Lane-Emden Equation (1) or (2) then, 
, (A = constant) is also a solution of the of Equation (1) and 
is also a solution of the Equation (2) [6].
Thus, if one solution 
of the Lane-Emden equation is known, we can derive a whole homologous family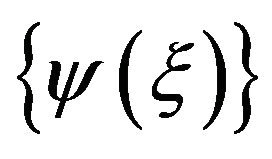 
of solutions. In particular, if 
is just the Lane-Emden function defined by the initial conditions of Equation (3), then its homologous family 
defines a whole set of solutions that are all finite at the origin 
Solutions that are finite at the origin are called E-solutions and denoted by
. The Lane-Emden function defined by the initial conditions from Equation (3) is just a particular member of the set 
of E-solutions. All E-solutions can be found from the Lane-Emden function through the homology transformations
, (4.1)
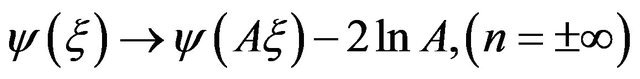. (4.2)
It should also be noted that, any solution 
that is finite at the origin 
is an E-solution, and its derivative is zero 
The general solution of the second order Lane-Emden equation must characterized by two integration constants. According to the homology theorem one of the two constants must be “trivial” in the sense that it defines merely the scale factor A of the homology transformation, and we should be able throughout the introduction of two independent homology invariant functions to transform the second order Lane-Emden equation into a first order differential equation [7].
3.2. Homology Invariant Functions
In what follows the definition and the basic properties of the homology invariant functions are 1) A function Q (say) is said to homology invariant if it is invariant to the homologous transformations:
(5.1)
or
(5.2)
So, to prove that, Q is homology invariant function, we have to prove that
(6)
2) The homology transformation for the derivatives are:
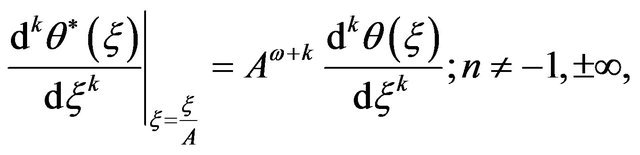(7.1)
(7.2)
4. New Generating Sets of Homology Invariant Functions
In this section, two new generating sets, (one for
, 
, and other for
) of homology invariant functions will be established1)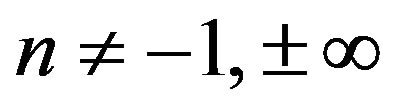 
(8)
where 
and k1 are real numbers, while k2 and 
are given in terms of 
and k1 and the polytropic index n 
from
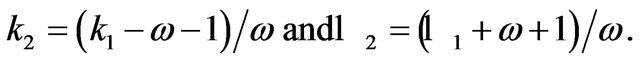(9)
The two functions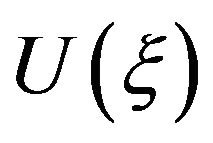 
and 
are homology invariant functions.
Proof. Since
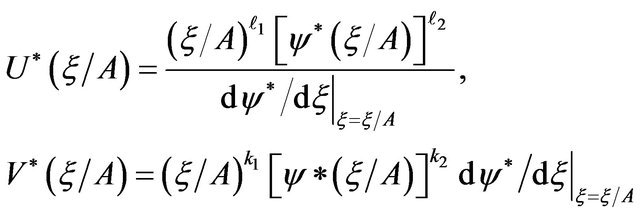
Applying the rules of Equations (5.1) and (7.1) we get
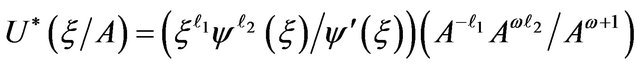
and
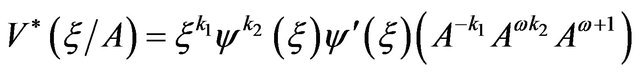
Using the values of 
and k2 from Equation (9) we get
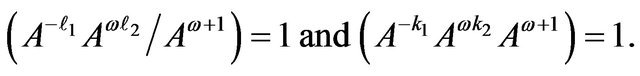
So
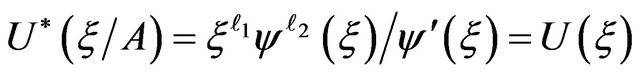
and
.
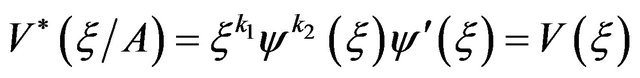That is, the two functions 
and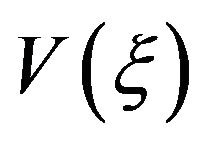 
are homology invariant functions. 
2) 
and
(10)
where k, m1 and m2 are real numbers.
The two functions 
and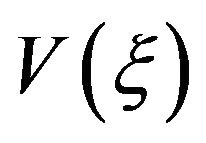 
are homology invariant functions.
Proof. Since
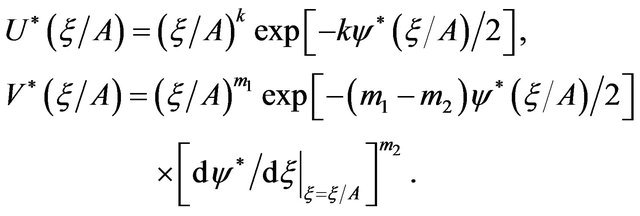
Applying the rules of Equations (5.2) and (7.2) we get
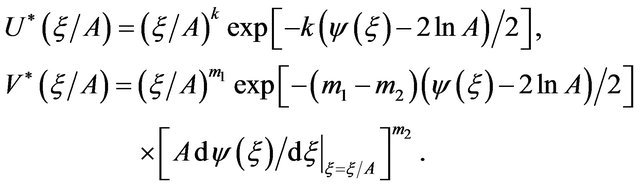
So
That is the two functions 
and 
are homology invariant functions. 
5. Reduction to the First Order-Differential Equation
Now, since the two functions 
and 
are homology invariant functions with respect to the transformations of the homology theorem, then we can reduce with the aid of these functions the second order LaneEmden equation to one of the first order. This will be of the subject of the present section.
1) 
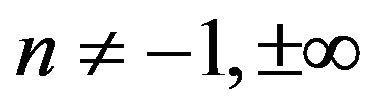
Since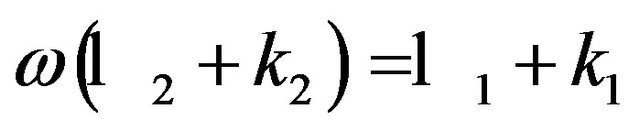
, then we get from Equation (8) that
(11)
Also from Equation (8) we have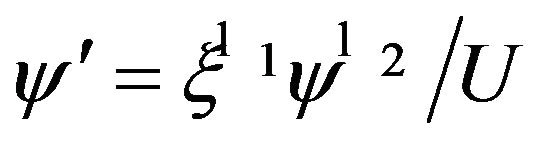
, then by using Equation (11) we get
(12)
where
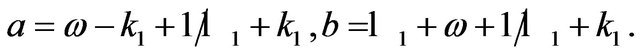
We have also from the original Lane-Emden equation
(13)
Differentiating Equations (8) logarithmically and then using Equations (11) and (12) we obtain
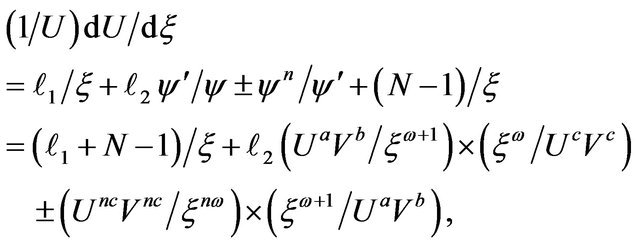
where 
Then
(14)
where
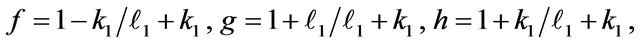
and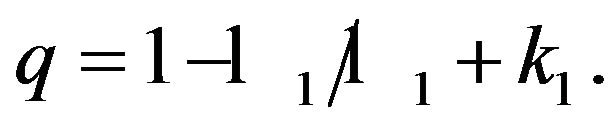 
Similarly we get
(15)
The required differential equation between U and V is obtained by dividing Equations (14) and (15) and we get for,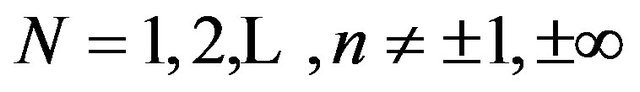 
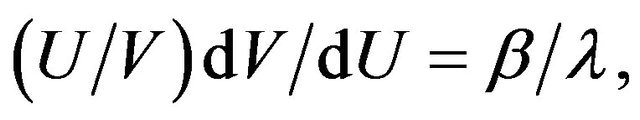(16)
where
2) 
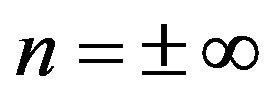
Form Equation (10) we get
(17)
(18)
From Equations (18) and (10) we have
(19)
We have also from the original Lane-Emden equation
(20)
From this equation and Equation (18) we get
(21)
From Equations (10) and (18)
(22)
Similarly we get
(23)
The required differential equation between U and V is obtained by dividing Equations (22) and (23) and we get for,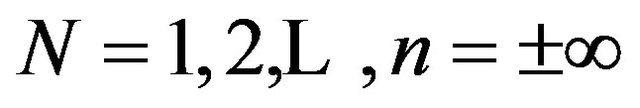 
where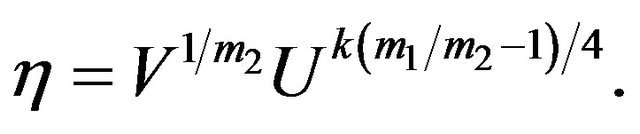 
6. Conclusion
In concluding the present paper, we stress that, two new generating sets, of homology invariant functions was established. Moreover, by the aid of two independent homology invariant functions of each set we established the transformed first order Lane-Emden equation. The first equation for polytropic index 
depends on five free parameters, while, the other equation is for, 
and depends on three free parameters.
NOTES