1. Introduction
A topological dynamical system (TDS) is a pair  such that X is a compact metric space and T is a homeomorphism. Our main concern is rigidity. This notion was first introduced by Furstenberg and Wiess for measure theoretical dynamical system (MDS); then Glasner and Maon defined the topological version of this notion [1].
such that X is a compact metric space and T is a homeomorphism. Our main concern is rigidity. This notion was first introduced by Furstenberg and Wiess for measure theoretical dynamical system (MDS); then Glasner and Maon defined the topological version of this notion [1].
A comprehensive study for rigidity in MDS has been done in [2]. In MDS, these are interesting; because, it is well-known that a generic transformation is rigid [3]. In this respect and in TDS, Glasner and Maon [1] established examples to show that even in minimal weakly mixing systems, there are plenty of examples with uniformly rigidity.
Let us recall the main definitions. An MDS 
is rigid along  if
if , as
, as  for all
for all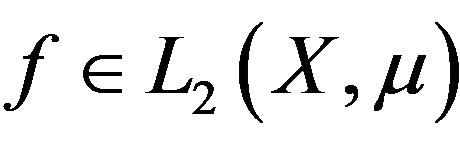 . A TDS
. A TDS  is called rigid if there exists a sequence
is called rigid if there exists a sequence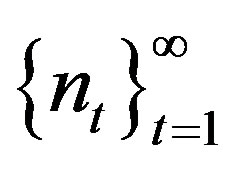 , called the rigidity sequence, such that
, called the rigidity sequence, such that  for any
for any ; it is called uniformly rigid if
; it is called uniformly rigid if  uniformly on X.
uniformly on X.
Let , then
, then
 (1.1)
(1.1)
is called the upper density of A and it is called lower density or density if we replace limsup in (1.1) with liminf or lim respectively. We call

the upper Banach density of a set .
.
In a TDS, the return time set is defined to be
 where U and V are opene (nonempty and open) sets. A TDS
where U and V are opene (nonempty and open) sets. A TDS  is transitive if for any two opene sets
is transitive if for any two opene sets 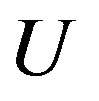 and
and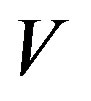 , we have
, we have ; and it is weak mixing if the product system
; and it is weak mixing if the product system  is transitive. A TDS
is transitive. A TDS  is mild mixing if for any transitive
is mild mixing if for any transitive , the product system
, the product system  is transitive; and it is strong mixing if
is transitive; and it is strong mixing if  is cofinite for opene sets
is cofinite for opene sets .
.
A collection of subsets of integers  is called family if it is hereditary upward: if
is called family if it is hereditary upward: if  and
and , then
, then .
.
It is well-known that mild mixing systems do not have uniformly rigid factors while minimal equicontinuous systems have comparatively large rigidity sequences. Therefore, one expects to have rigidity along large sequences is system with low complexity. In this note, we define some other classes of mixings. These are defined when  generates a certain family of integers
generates a certain family of integers . In particular, we use this concept and define
. In particular, we use this concept and define  -mixings and we show that minimal
-mixings and we show that minimal  - mixings do not have any rigidity factor.
- mixings do not have any rigidity factor.
2. Main Results
It is well known that in a transitive TDS, any almost equicontinuous is uniformly rigid [1]. In [4] the authors showed that a uniformly rigid mild mixing dynamical system is trivial. Also in [1], Glasner and Maon constructed a generic minimal uniformly rigid weakly mixing. On the other hand, any system with rigidity sequence has zero entropy [1]. Therefore, a uniformly rigid TDS with zero entropy is generic. However, there are some restrictions for a sequence to be a rigidity sequence. The following shows some of these restrictions which are compatible with the rigidity sequences in MDS [5, Proposition 2.20 (b), 2.24 and 2.26].
Theorem 2.1. Let  be an increasing sequence in
be an increasing sequence in  and suppose that for any
and suppose that for any ,
, .
.
1) If T is rigid along A, then A has gaps tending to infinity.
2) Suppose  where
where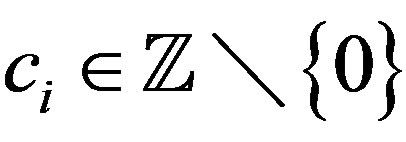 . If for each
. If for each , there is
, there is  such that
such that , then A is not a rigidity sequence for any TDS.
, then A is not a rigidity sequence for any TDS.
3) Suppose A has the property that for some integers . Then A cannot be a rigidity sequence for a TDS. In particular,
. Then A cannot be a rigidity sequence for a TDS. In particular, .
.
Proof. We prove only (1) and the two others follow similarly. Let  be rigid along
be rigid along . Then
. Then  for every
for every . By the dominated convergence theorem for every invariant measure and in particular for ergodic measure
. By the dominated convergence theorem for every invariant measure and in particular for ergodic measure  and any
and any  we have
we have . This shows that
. This shows that  is rigid along
is rigid along  in measure theoretical sense. By [5, Proposition 2.20(b)], if
in measure theoretical sense. By [5, Proposition 2.20(b)], if  is a rigidity sequence for ergodic
is a rigidity sequence for ergodic , then
, then  has gaps tending to infinity.
has gaps tending to infinity.
Note that the second part of the conclusion in (2) follows from the fact that sets having positive upper Banach density have a certain distance appearing infinitely many times.
If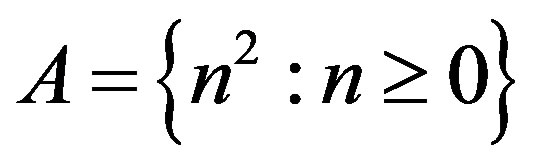 , then
, then  and so it has positive density. Therefore,
and so it has positive density. Therefore,  cannot be a uniformly rigidity sequence for any
cannot be a uniformly rigidity sequence for any  . This is also true for sequence of prime numbers and polynomial sequence with integer coefficients.
. This is also true for sequence of prime numbers and polynomial sequence with integer coefficients.
Let
 . (2.1)
. (2.1)
From largeness point of view,  is next to the family of positive upper density, that is, if
is next to the family of positive upper density, that is, if 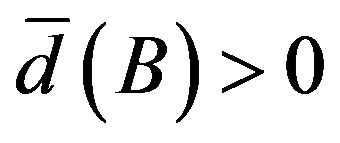 then
then 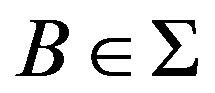 [6]. This family has many interesting properties and it is a long standing conjecture by Erdös that any member of this family has arbitrary long arithmetic progression. In the following example we show that there are some uniformly rigid TDS whose rigidity sequence is in
[6]. This family has many interesting properties and it is a long standing conjecture by Erdös that any member of this family has arbitrary long arithmetic progression. In the following example we show that there are some uniformly rigid TDS whose rigidity sequence is in .
.
Example 2.2. Let  and T the irrational rotation on
and T the irrational rotation on  (or consider any equicontinuous minimal system). Note that for any
(or consider any equicontinuous minimal system). Note that for any  and any opene set U, the return time set
and any opene set U, the return time set  is syndetic and if rigidity is established for a point
is syndetic and if rigidity is established for a point , that is if there exists
, that is if there exists  such that
such that , then rigidity is established for all points. Also rigidity and uniform rigidity are equivalent for our system.
, then rigidity is established for all points. Also rigidity and uniform rigidity are equivalent for our system.
First we construct a rigidity sequence  and then we will show that
and then we will show that  which is trivially a rigidity sequence is in
which is trivially a rigidity sequence is in . So let
. So let  and let
and let 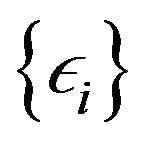 be a decreasing sequence to zero and set
be a decreasing sequence to zero and set  to be the sequence with
to be the sequence with  the maximum gap for
the maximum gap for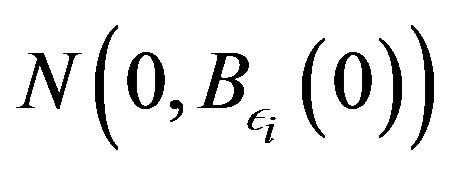 .
.
Set ,
,  and pick consecutive
and pick consecutive
 . For any
. For any  we have
we have 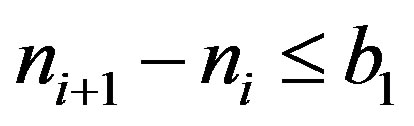 and
and 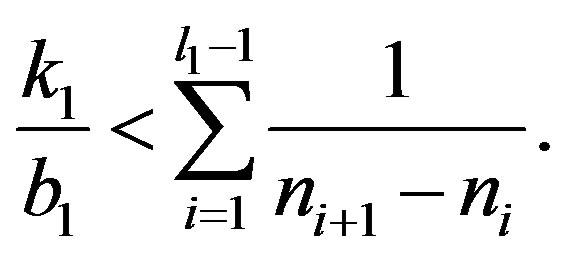
Use induction argument and let
 such that
such that . So
. So  and thus
and thus . But for any
. But for any  which implies
which implies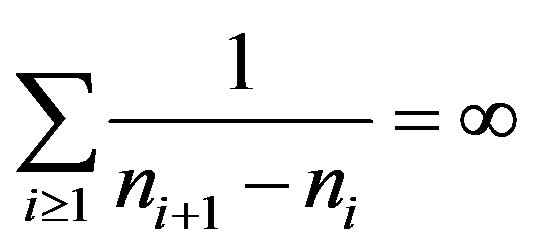 .
.
Remark 2.3.
1) Let . Then
. Then 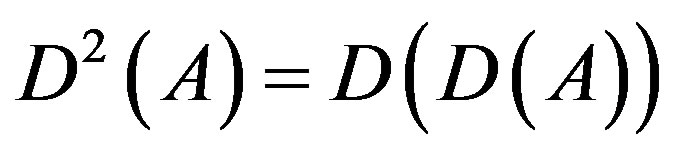 and in general
and in general  can be defined for any
can be defined for any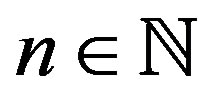 . In [7], for any
. In [7], for any , an explicit subset of
, an explicit subset of  such as
such as  depending on n is given such that
depending on n is given such that . Now the existence of such sets is established by the above example and Theorem 2.1(3). In fact, we have more: there is
. Now the existence of such sets is established by the above example and Theorem 2.1(3). In fact, we have more: there is  such that for any
such that for any ,
, .
.
2) If  along a subsequence
along a subsequence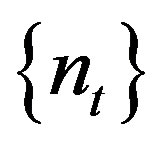 , then
, then  is rigid along
is rigid along 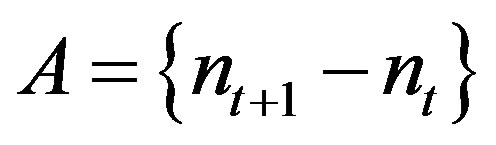 and it is uniform rigid if
and it is uniform rigid if  is uniform. If
is uniform. If  is also rigid along
is also rigid along , then
, then  is rigid and it is uniform if both
is rigid and it is uniform if both  and
and  are uniformly rigid along
are uniformly rigid along .
.
Theorem 2.4. Suppose  is rigid along
is rigid along  and
and 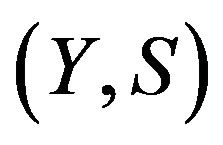 a TDS. Then
a TDS. Then  is rigid if there exists
is rigid if there exists  and
and  such that
such that  is rigid along
is rigid along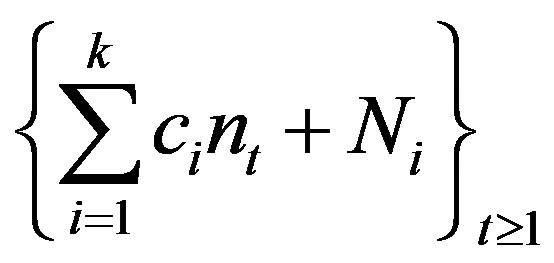 .
.
Proof. If  is rigid along
is rigid along , then it is also rigid along
, then it is also rigid along  for any
for any  and
and .
.
Corollary 2.5. Let 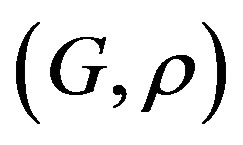 be a rotation and
be a rotation and  a rigid (resp. uniformly rigid) system. Then
a rigid (resp. uniformly rigid) system. Then  is rigid (resp. uniformly rigid).
is rigid (resp. uniformly rigid).
Proof. Suppose 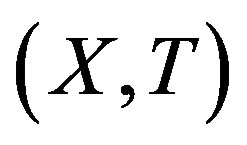 is rigid along some sequence
is rigid along some sequence . Let
. Let  be the rotation map. For any
be the rotation map. For any , by passing to a subsequence if necessary, we have
, by passing to a subsequence if necessary, we have  for some
for some . This means that
. This means that 
where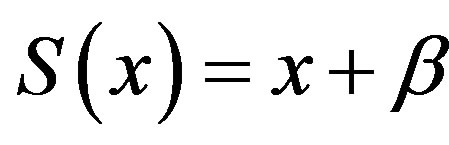 . Hence
. Hence 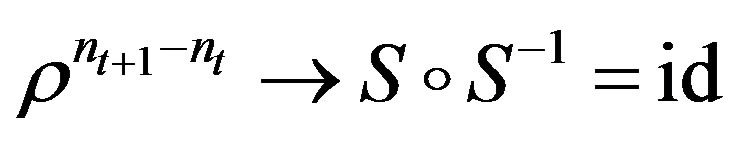 uniformly and
uniformly and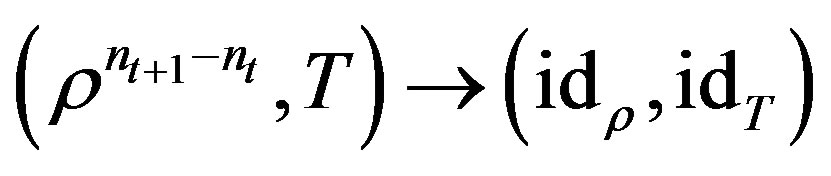 .
.
Theorem 2.6. Suppose 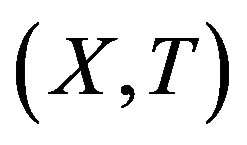 is rigid. Then any factor is rigid.
is rigid. Then any factor is rigid.
Proof. This is clearly true for the trivial factor. So let  be rigid along
be rigid along  and
and  a nontrivial factor with factor map
a nontrivial factor with factor map . We show that
. We show that  is rigid along a subsequence of
is rigid along a subsequence of . To this end, let
. To this end, let 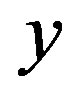 be an arbitrary point in
be an arbitrary point in ,
,  and
and 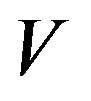 an opene set containing
an opene set containing . Since
. Since  is rigid there exists
is rigid there exists  such that for any
such that for any . Thus
. Thus  and so
and so .
.
Let  be a family of nonempty subsets of
be a family of nonempty subsets of . The dual of
. The dual of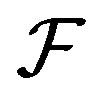 , denoted by
, denoted by , is defined to be all subsets of
, is defined to be all subsets of  meeting all sets in
meeting all sets in :
:

A family  is called partition regular if
is called partition regular if  is partitioned to finite sets
is partitioned to finite sets , then there is
, then there is 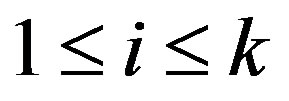 such that
such that . An example of a family with partition regularity is the family
. An example of a family with partition regularity is the family 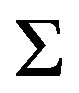 defined as (2.1). A nonempty family closed under finite intersections is called a filter. It is known that if
defined as (2.1). A nonempty family closed under finite intersections is called a filter. It is known that if  is partition regular, then
is partition regular, then 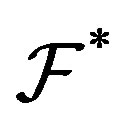 is a filter. A filter which is partition regular is called an ultrafilter.
is a filter. A filter which is partition regular is called an ultrafilter.
Now let 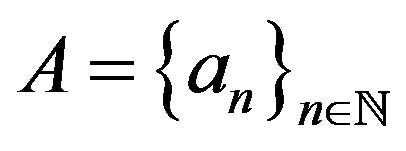 be an increasing sequence of integers. Then
be an increasing sequence of integers. Then  is the finite sums of A. A set
is the finite sums of A. A set  is called an IP-set if it contains the finite sums of some sequence of integers. A set
is called an IP-set if it contains the finite sums of some sequence of integers. A set  is called a ∆-set if a sequence of integers
is called a ∆-set if a sequence of integers  exists such that the difference set
exists such that the difference set
 . Let ∆ be the family of all
. Let ∆ be the family of all
∆-sets. Any IP-set is a ∆-set for let
 . Let
. Let  (resp. ∆) be the family of all IP-sets (resp. ∆-sets). It is known that the families
(resp. ∆) be the family of all IP-sets (resp. ∆-sets). It is known that the families  and
and  are filters [8].
are filters [8].
Definition 2.7. A TDS  is called
is called  -transitive if for any two opene sets
-transitive if for any two opene sets  we have
we have  , and it is called
, and it is called 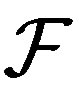 -mixing if the product system
-mixing if the product system  is
is  -transitive.
-transitive.
Theorem 2.8. [9] Let  be a TDS. The following conditions are equivalent:
be a TDS. The following conditions are equivalent:
1)  is
is  -mixing;
-mixing;
2)  is weak mixing and
is weak mixing and  -transitive;
-transitive;
3)  for any opene sets U, V.
for any opene sets U, V.
For a family  and
and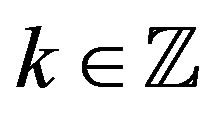 , the shifted family is defined as
, the shifted family is defined as  where
where
 . If
. If  for any
for any , then
, then  is called a shift invariant family. For instance, if
is called a shift invariant family. For instance, if , then both
, then both  and
and  are shift invariant families. But not all families are shift invariant. There are two ways to build a shift invariant family from a given
are shift invariant families. But not all families are shift invariant. There are two ways to build a shift invariant family from a given  [8]. These are
[8]. These are  and
and  where
where

We have  and both
and both  and
and  are shift invariant families with
are shift invariant families with  [8]. Also, if
[8]. Also, if
 then
then 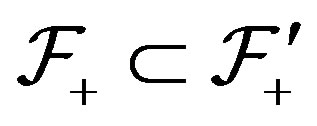 and
and  which implies that
which implies that . If
. If  is a filter so is any shift of
is a filter so is any shift of  and since the finite intersections of filters are again filters
and since the finite intersections of filters are again filters  is a filter.
is a filter.
Theorem 2.9.
1)  is
is 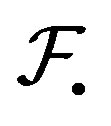 -transitive if and only if it is
-transitive if and only if it is  -transitive.
-transitive.
2) Suppose  is a filter. Then
is a filter. Then  is
is  -mixing if and only if it is
-mixing if and only if it is  -mixing.
-mixing.
Proof. 1) We have , so
, so  -transitive is
-transitive is  - transitive. Conversely, suppose
- transitive. Conversely, suppose  is
is  -transitive. Then for any opene U and V, we have
-transitive. Then for any opene U and V, we have . Since
. Since  is opene for
is opene for ,
,  . This means that for
. This means that for ,
,  which in turn implies
which in turn implies 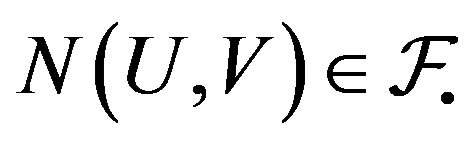 .
.
2) This is a direct consequence of the first part and Theorem 2.8.
Theorem 2.10. Let  be a filter and
be a filter and  an
an  - mixing system. Then any non-trivial factor of
- mixing system. Then any non-trivial factor of  is also
is also  -mixing.
-mixing.
Proof. Suppose  is
is 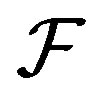 -mixing and
-mixing and  a non-trivial factor and
a non-trivial factor and  the factor map:
the factor map: . For any two opene sets U,
. For any two opene sets U,  ,
,  . We will show that this will hold for
. We will show that this will hold for  as well.
as well.
Let  be two opene sets in Y and let
be two opene sets in Y and let  such that
such that . Then
. Then

Since  is a family, so
is a family, so . Also, since
. Also, since  is a filter
is a filter  which implies
which implies  is
is  -mixing.
-mixing.
Let  be a family of subsets of integers closed under finite intersections (in general like a filter). Then we say that a sequence
be a family of subsets of integers closed under finite intersections (in general like a filter). Then we say that a sequence 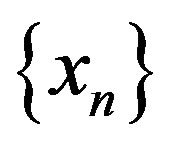 is
is 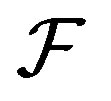 -convergent to
-convergent to  if for any neighborhood
if for any neighborhood  of
of  we have
we have
 and we write
and we write .
.
A family is called an  family if any member contains the difference set of an IP-set.
family if any member contains the difference set of an IP-set.
Theorem 2.11. Let  be uniformly rigid along
be uniformly rigid along
 . Then
. Then .
.
Proof. First we prove that  id. Let
id. Let  be uniformly rigid along
be uniformly rigid along . Fix
. Fix 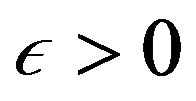 and let
and let  be an increasing sequence and each
be an increasing sequence and each  sufficiently large so that
sufficiently large so that

Hence for any  we have
we have
 (2.2)
(2.2)
Now set . Then
. Then  contains B and so is an IP-set.
contains B and so is an IP-set.
To see that , note that if
, note that if  is a rigidity sequence so is
is a rigidity sequence so is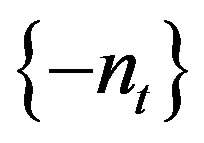 . Then an inequality such as (2.2) implies that
. Then an inequality such as (2.2) implies that  where
where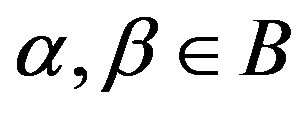 .
.
Now we investigate the existence of rigidity (not necessarily uniform) in minimal systems with some sort of mixings. Recall that a minimal system is mild mixing if and only if it is  -mixing if and only if it is
-mixing if and only if it is
 -transitive [10].
-transitive [10].
A pair  is said to be a proximal pair if
is said to be a proximal pair if

and  is proximal system if any pair of
is proximal system if any pair of  is a proximal pair. A TDS
is a proximal pair. A TDS  is called distal if
is called distal if  for every
for every  and
and  . In [1], the authors showed that any minimal strong mixing system admits only trivial rigid factors. An extension of that result is the following.
. In [1], the authors showed that any minimal strong mixing system admits only trivial rigid factors. An extension of that result is the following.
Theorem 2.12. Suppose  is a filter. Then a minimal
is a filter. Then a minimal 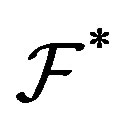 -mixing system does not have
-mixing system does not have  -rigid factor where
-rigid factor where .
.
Proof. Let 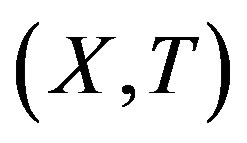 be a minimal
be a minimal  -mixing. Then by Theorem 2.9 and Theorem 2.10, every factor of
-mixing. Then by Theorem 2.9 and Theorem 2.10, every factor of  is
is  -mixing. Thus it is sufficient to show that if
-mixing. Thus it is sufficient to show that if 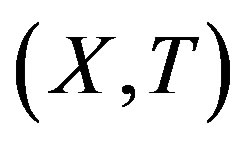 is
is  -rigid, then it must be trivial. Assume that
-rigid, then it must be trivial. Assume that  is rigid with respect to an
is rigid with respect to an  sequence
sequence .
.
Let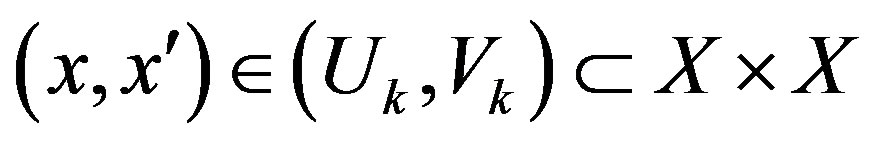 , where
, where 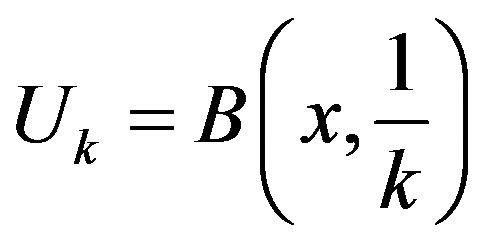 and
and . Note that
. Note that  is
is 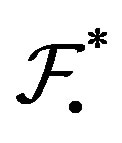 and so
and so
 . Therefore, there exists a subsequence
. Therefore, there exists a subsequence  of
of  such that
such that
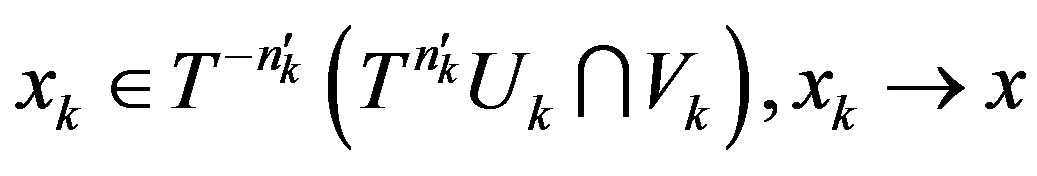 and
and . Which implies that
. Which implies that  is a proximal pair. Since
is a proximal pair. Since  was arbitrary the system is proximal. But in a minimal system,
was arbitrary the system is proximal. But in a minimal system,  is distal for any x and this in turn implies that
is distal for any x and this in turn implies that 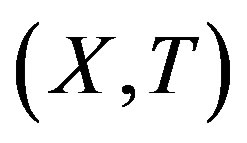 must be trivial.
must be trivial.
Corollary 2.13.
1) A minimal  -mixing system does not have any rigid factor.
-mixing system does not have any rigid factor.
2) A minimal 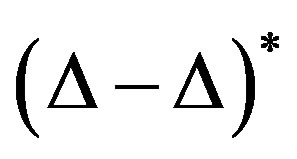 -transitive system is not rigid.
-transitive system is not rigid.
3) Any  -mixing, IP*-mixing or
-mixing, IP*-mixing or  -transitive system does not have a non-trivial uniformly rigid factor.
-transitive system does not have a non-trivial uniformly rigid factor.
Proof.
1) By Theorem 2.10, it suffices to show that a minimal  -mixing
-mixing  is not rigid along any
is not rigid along any . Assume the contrary and let
. Assume the contrary and let  be a sequence decreasing to zero. Let
be a sequence decreasing to zero. Let , where
, where  are
are  -balls containing
-balls containing  and
and 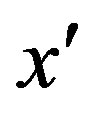 respectively. Then there exists
respectively. Then there exists 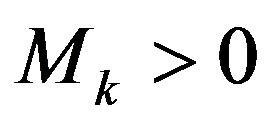 such that for any
such that for any
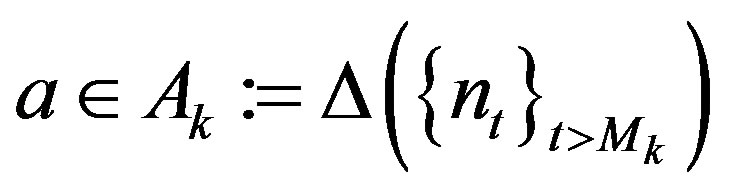 ,
, . Since
. Since  is
is
 ,
, . Now if
. Now if , then there exists a subsequence
, then there exists a subsequence  and a sequence
and a sequence  such that
such that 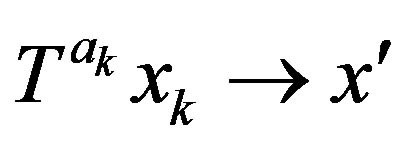 and
and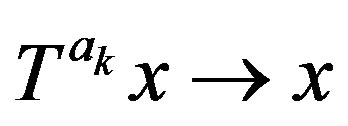 . Now an argument as in the proof of Theorem 2.12 gives the proof.
. Now an argument as in the proof of Theorem 2.12 gives the proof.
2) The proof is similar to (1).
3) Recall that any  -mixing, IP*-mixing and
-mixing, IP*-mixing and  -transitive is trivially an
-transitive is trivially an 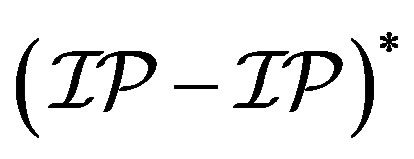 -transitive. Now the conclusion follows from the fact that mild mixing systems do not have non-trivial uniform rigid factors.
-transitive. Now the conclusion follows from the fact that mild mixing systems do not have non-trivial uniform rigid factors.