Lower Hemi-Continuity, Open Sections, and Convexity: Counter Examples in Infinite Dimensional Spaces ()
1. Introduction
Correspondences with open lower sections play an important role in general equilibrium analysis and in game theory. In general, the lower sections of a lower hemicontinuous (lhc) correspondence need not be open. However, for an lhc correspondence with upper sections that are open and convex in Rn, we have the following result (Proposition 11.70 in [1], Theorem 5.9 in [2]):
Theorem 1. Let  be a correspondence from a Hausdorff space X to Rn. If
be a correspondence from a Hausdorff space X to Rn. If  is lower hemi-continuous with upper sections (values) that are convex and open in
is lower hemi-continuous with upper sections (values) that are convex and open in  then S has open lower sections.
then S has open lower sections.
When  has convex lower and upper sections, the above theorem implies that
has convex lower and upper sections, the above theorem implies that 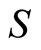 is lhc with open upper sections, if and only if
is lhc with open upper sections, if and only if , the inverse of
, the inverse of , is lhc with open upper sections.
, is lhc with open upper sections.
Theorem 1 has several applications in economics. For example, the statement “since  and
and  is continuous, it follows that
is continuous, it follows that  in some neighborhood of
in some neighborhood of ” appears in the proof of a well-known theorem regarding the differentiability of the value function (Theorem 4.11, page 85 in [3]) (the set
” appears in the proof of a well-known theorem regarding the differentiability of the value function (Theorem 4.11, page 85 in [3]) (the set  denotes the interior of
denotes the interior of ). The justification of this claim relies on Theorem 1; the correspondence
). The justification of this claim relies on Theorem 1; the correspondence  has a range in Rn, and it is continuous with a convex graph. This implies that the correspondence
has a range in Rn, and it is continuous with a convex graph. This implies that the correspondence  is lhc with open and convex upper sections, and the statement quoted from [3] follows immediately.1
is lhc with open and convex upper sections, and the statement quoted from [3] follows immediately.1
For more on the application of Theorem 1 in establishing the differentiability of value functions, see [5] and Kim [6]. Theorem 1 has also been used to establish the existence of continuous selections, fixed points of best reply functions, and to establish the existence of equilibria for non-ordered preferences in abstract economies [7-10]. It is straightforward to show that Theorem 1 does not hold if the convexity requirement on the upper sections of S is dropped. It is also relatively easy to demonstrate that this theorem does not hold, if the upper sections of S are convex but are not open in Rn (see page 237 in [11] and page 9 in [12]). Keeping all the other assumptions the same, does the above theorem hold if Rn is replaced with an arbitrary locally convex (infinitedimensional) space? (for examples of economic applications involving correspondences with values that are not in Rn see [13-20]). As far as we know, there has not been a satisfactory answer to this question. In fact, in his book Mathematical Methods for Economists, Moore (page 273 in [1]) states “it may well be that Holly’s proposition [Theorem 1] can be generalized to the extent of substituting an arbitrary locally convex Hausdorff space in place of Rn, although I am not sure whether or not this conjecture is correct”. In this note, we show that the answer to our question is no, and that the above conjecture is incorrect.
2. Two Counter-Examples
Recall that a correspondence  is lhc at some point
is lhc at some point , if for every open set
, if for every open set  in Y such that
in Y such that , there exists an open neighborhood
, there exists an open neighborhood  of
of  such that
such that 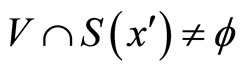 for all
for all  When
When  is first countable, this definition is equivalent to the following: for any open set
is first countable, this definition is equivalent to the following: for any open set  in Y such
in Y such , and for any sequence
, and for any sequence  there exists
there exists  such that
such that 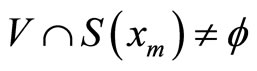 for all
for all  Let
Let 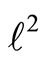 be the space of square summable sequences in R. This is a separable Hilbert space with an inner product that we shall denote by
be the space of square summable sequences in R. This is a separable Hilbert space with an inner product that we shall denote by . Let
. Let  be the standard orthonormal base in
be the standard orthonormal base in  (the vector
(the vector  has 1 in the nth position and zeros everywhere else). Let A be the collection
has 1 in the nth position and zeros everywhere else). Let A be the collection  and let
and let  Let
Let  be the unit ball
be the unit ball  in
in  equipped with the weak topology (i.e. W is open in X, if and only if
equipped with the weak topology (i.e. W is open in X, if and only if  for some set W' that is weakly open in
for some set W' that is weakly open in ). Note that A0 is the closure of A in the weak topology of
). Note that A0 is the closure of A in the weak topology of . Therefore, X\A is not open in X but X\A0 is. Finally, let Y be the space
. Therefore, X\A is not open in X but X\A0 is. Finally, let Y be the space  equipped with the weak topology. The space Y is an infinite-dimensional locally convex Hausdorff topological vector space. Since the unit ball in a separable reflexive Banach space is metrizable in the weak topology (Theorem 3.16 in [21]), X is metrizable even though Y is not.
equipped with the weak topology. The space Y is an infinite-dimensional locally convex Hausdorff topological vector space. Since the unit ball in a separable reflexive Banach space is metrizable in the weak topology (Theorem 3.16 in [21]), X is metrizable even though Y is not.
Lemma 1. For every  let
let
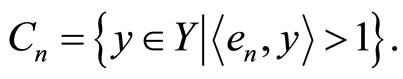
The set  is dense in Y.
is dense in Y.
Proof. For every  let
let  except for the nth component, which is set to be equal to 2 (anything bigger than 1 will work). For every
except for the nth component, which is set to be equal to 2 (anything bigger than 1 will work). For every 
 and hence
and hence  Moreover, for every
Moreover, for every 
 and therefore zn converges weakly to z.
and therefore zn converges weakly to z.
Lemma 2. Let  be defined as in Lemma 1. Let
be defined as in Lemma 1. Let  be a correspondence defined as follows:
be a correspondence defined as follows:

Then, S is lower hemi-continuous with upper sections that are open and convex in Y.
Proof. By the definition of the weak topology, for every  the set
the set  is open in the weak topology. Hence, it is clear that for any
is open in the weak topology. Hence, it is clear that for any 
 is convex and open in Y. Let
is convex and open in Y. Let  and let V be an open set in Y such that
and let V be an open set in Y such that  Since
Since  is open in
is open in , there exists a neighborhood
, there exists a neighborhood  of x such that
of x such that  and
and  for all
for all  Hence, S is lhc at x Now let
Hence, S is lhc at x Now let  be some element in A, and let
be some element in A, and let  in X, and without loss of generality assume that xn is not the constant sequence
in X, and without loss of generality assume that xn is not the constant sequence  There exists m0 such that for all
There exists m0 such that for all 
 . Otherwise, we can obtain a subsequence
. Otherwise, we can obtain a subsequence  of
of  such that
such that  weakly, contradicting the fact that
weakly, contradicting the fact that  has a unique weak limit (the sequence 0) given the fact that X is Hausdorff. Now this implies that
has a unique weak limit (the sequence 0) given the fact that X is Hausdorff. Now this implies that  for all
for all  Hence, S is lhc at
Hence, S is lhc at , and therefore it is lhc at any point in A. We still need to show that S is lhc at
, and therefore it is lhc at any point in A. We still need to show that S is lhc at  Assume S is not lhc at zero. Then, there exists an open set V in Y such that
Assume S is not lhc at zero. Then, there exists an open set V in Y such that  and there exists
and there exists  in X such that
in X such that  for all n. This sequence has to be a subset of A (i.e. a subsequence of
for all n. This sequence has to be a subset of A (i.e. a subsequence of ) since
) since  for any
for any . Without loss of generality, simply assume
. Without loss of generality, simply assume 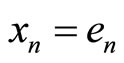 for all n. Let
for all n. Let  By Lemma 1, there exists a sequence
By Lemma 1, there exists a sequence  such
such  converges weakly to z, and therefore
converges weakly to z, and therefore  for some n, a contradiction. Hence, S is lhc at zero.
for some n, a contradiction. Hence, S is lhc at zero.
Proposition 1. Let S be defined as in Lemma 2. Then, S is lower hemi-continuous with upper sections that are open and in convex in Y, and yet S does not have open lower sections.
Proof. By Lemma 2, S is lower hemi-continuous with upper sections that are open and in convex in Y. Moreover,  which is not an open set in X.
which is not an open set in X.
The closed graph theorem for correspondences asserts that a closed-valued correspondence with a compact range is upper hemi-continuous, if and only if it has a closed graph (Proposition 17.11 in [22]). This result, particularly when combined with Kakutani’s fixed point theorem, has important applications in economics. It is then natural to ask if there exists an “open graph” theorem, i.e. a theorem asserting that a lower hemi-continuous correspondence with open and convex values is lower hemi-continuous, if and only if it has an open graph.2 The fact that this statement does in fact hold when the range of S is Rn was proved Zhou who used this result to establish the existence of equilbria in various qualitative games.
Theorem 2. (Proposition 2 in [24]). Let S be a correspondence from a Hausdorff space X to Rn. If S is lower hemi-continuous with open and convex upper sections in Rn, then S has an open graph.
The setting of Proposition 1 can be slightly modified to show that when S has an infinite dimensional range, Theorem 2 may not hold, even under the additional assumption that S has open lower sections (Bergstrom, Parks, and Rader in [23] provided an example of a correspondence with open upper and lower sections but whose graph was is not open, In their example, however, the correspondence has non-convex upper section).
Proposition 2. Let X and Y be defined as before. Let 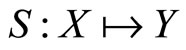 be defined by
be defined by

Then S is lhc with open and convex upper and lower sections in Rn, yet the graph of S is not open.
Proof. Clearly, S has open and convex upper and lower sections (in X and Y respectively). Assume S has an open graph in  which means that set
which means that set

is open in  This implies that the set
This implies that the set

is closed in  The sequence
The sequence  is contained in
is contained in  yet
yet  the limit of this sequence in the product topology on
the limit of this sequence in the product topology on  is not. This contradicts the fact that
is not. This contradicts the fact that  is closed. Therefore the graph of S is not open.
is closed. Therefore the graph of S is not open.
Similar counter-examples based on Propositions 1 and 2 can be constructed if  is replaced with any Hilbert space H and Y is taken to be H equipped with the weak topology (for economic applications where the underlying space is equipped with the weak topology, see [13] and [18]).
is replaced with any Hilbert space H and Y is taken to be H equipped with the weak topology (for economic applications where the underlying space is equipped with the weak topology, see [13] and [18]).
3. Conclusions
For a lower hemi-continuous correspondence S with values in a finite dimensional Euclidean space, the convexity of the upper and lower sections has very strong topological implications (Theorems 1 and 2) that can used to obtain existence results for maximal elements, fixed points, continuous selections, and Nash equilibria. However, there is an increasing number of economic applications that involve correspondences with values in infinite-dimensional spaces. Some of these applications consist of dynamic choice models over an infinite horizon [14]. Other applications consist of general equilibrium models that allow for infinite variation within the commodities of the economy. This includes variations in the physical attributes of the goods, time of delivery, and the state of the world when delivery takes place [12,13, 15-18,20,25]. Given the increasing interest in such applications, it is important to know whether or not the topological implications of the convexity of the upper and lower sections of S, valid when the range of S is Rn, still hold when the range of S is an arbitrary locally convex topological space. Propositions 1 and 2 in this note demonstrate that there is no hope of obtaining general results similar to Theorems 1 and 2, if Rn is replaced with an infinite-dimensional space. One approach to deal with this unfortunate fact is to impose additional assumptions on S–1. However, such assumptions often lack a clear economic interpretation, and they are more difficult to verify than simply assuming that S has open and convex upper sections. It is important to keep in mind that the counter-examples of this note only show that a particular method (Theorems 1 and 2) fails to establish the existence of certain elements of interest (maximal elements, continuous selection, fixed points, Nash equilibria) in infinite dimensional settings. These counter-examples do not rule out the possibility that other methods might succeed. Therefore, in applications involving infinite-dimensional spaces, finding sufficient conditions for the existence of maximal elements, continuous selections, fixed points, and Nash equilibria that can be imposed on S (rather than on S–1), and that can be easily interpreted and verified, continues to be a topic worthy of further investigation.
NOTES
2The question regarding the existence of an “open graph” theorem was raised first by Bergstrom, Park, and Rader [23].