Quantum Mechanics and the Philosophy of Language:Reconsideration of Traditional Philosophies ()
1. Introduction
Recently in [1-6] (finally, in [1]), we proposed (classical and quantum) measurement theory, which is characterized as the linguistic (or, metaphysical) approach to quantum mechanics. As seen in [1-6], this theory includes several conventional system theories (e.g. quantum system theory, statistics, dynamical system theory and so on). And thus, we believe that measurement theory is one of the most applicable theories in science.
The purpose of this paper is to show that quantum mechanics has a good linguistic philosophy, that is, to understand traditional philosophies in the framework of measurement theory, or equivalently, to explain the meaning of Figure 1. As shown in this paper, we consider that Figure 1 is natural, since the purposes of all theories in this figure are the same, that is, the world description (i.e., how to describe the world).
2. Measurement Theory
In this section, according to [1], we explain the outline (Figure 1: ②-③) of measurement theory (or in short, MT).
2.1. Axioms 1 and 2 of MT (Figure 1: ②-③)
Measurement theory ([1-6]) is, by an analogy of quantum mechanics (or, as a linguistic turn of quantum mechanics, cf. Figure 1: ③), constructed as the mathematical theory formulated in a certain C*-algebra A (i.e., a norm closed sub algebra in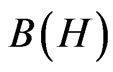 , cf. [7,8]). MT is composed of two axioms as follows:
, cf. [7,8]). MT is composed of two axioms as follows:

Figure 1. This figure (①-⑧) will be explained in this paper.

For completeness, note that measurement theory (A) is not physics but a kind of language based on “the quantum mechanical world view”.
When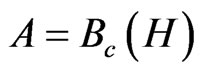 , the C*-algebra composed of all compact operators on a Hilbert space H, the (A) is called quantum measurement theory (or, quantum system theory), which can be regarded as the linguistic aspect of quantum mechanics. Also, when A is commutative (that is, when A is characterized by
, the C*-algebra composed of all compact operators on a Hilbert space H, the (A) is called quantum measurement theory (or, quantum system theory), which can be regarded as the linguistic aspect of quantum mechanics. Also, when A is commutative (that is, when A is characterized by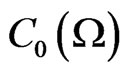 , the C*-algebra composed of all continuous complex-valued functions vanishing at infinity on a locally compact Hausdorff space Ω (cf. [7])), the (A) is called classical measurement theory. Thus, we have the following classification:
, the C*-algebra composed of all continuous complex-valued functions vanishing at infinity on a locally compact Hausdorff space Ω (cf. [7])), the (A) is called classical measurement theory. Thus, we have the following classification:

That is, this theory covers several conventional system theories (i.e., statistics, dynamical system theory, quantum system theory, etc.).
Now we shall explain the measurement theory (A). Let 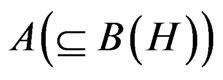 be a C*-algebra, and let A* be the dual Banach space of A. The norm
be a C*-algebra, and let A* be the dual Banach space of A. The norm 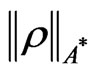 is defined by sup
is defined by sup
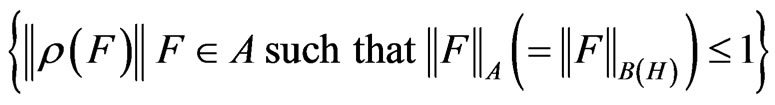 .
.
Define the mixed state 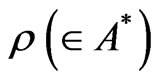 such that
such that 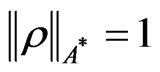 and
and 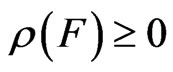 for all
for all 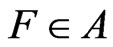 such that
such that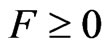 . And put
. And put
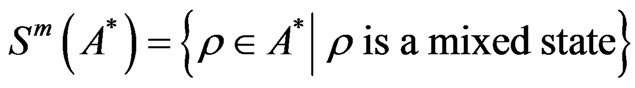 . (1)
. (1)
A mixed state ρ is called a pure state if it satisfies that “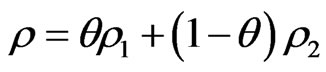 for some
for some 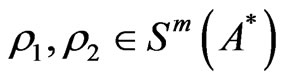 and 0 < θ < 1” implies
and 0 < θ < 1” implies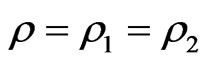 . Put
. Put
 , (2)
, (2)
which is called a state space. It is well known (cf. [7]) that
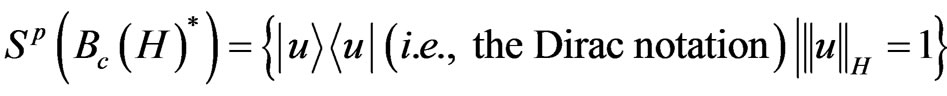 ,
,
and 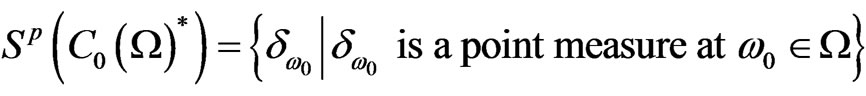 ,
,
where 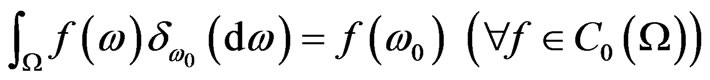 . The latter implies that
. The latter implies that 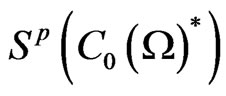 can be also identified with Ω (called a spectrum space, spectrum or maximal ideal space) such as
can be also identified with Ω (called a spectrum space, spectrum or maximal ideal space) such as
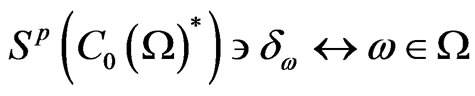 (3)
(3)
In this paper we assume that the C*-algebra 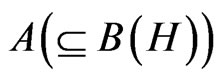 has the identity I. This assumption is not unnatural, since, if
has the identity I. This assumption is not unnatural, since, if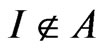 , it suffices to reconstruct the above A such that it includes
, it suffices to reconstruct the above A such that it includes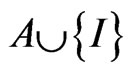 .
.
According to the noted idea (cf. [9]) in quantum mechanics, an observable 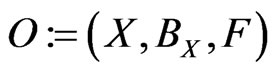 in A is defined as follows:
in A is defined as follows:
[1): Field] X is a set, BX ( 2X, the power set of X) is a field of X, that is, “
2X, the power set of X) is a field of X, that is, “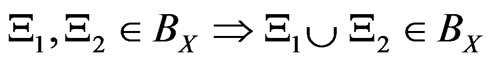 ”, “
”, “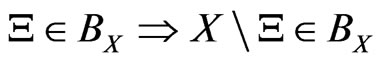 ”.
”.
[2): Additivity] F is a mapping from BX to A satisfying: 1): for every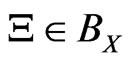 ,
, 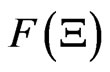 is a non-negative element in A such that
is a non-negative element in A such that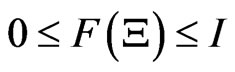 ; 2):
; 2): 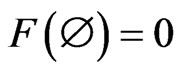 and
and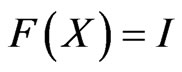 , where 0 and I is the 0-element and the identity in A respectively; 3): for any
, where 0 and I is the 0-element and the identity in A respectively; 3): for any 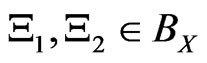 such that
such that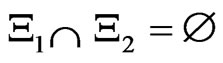 , it holds that
, it holds that 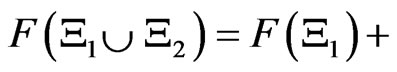
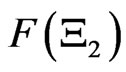 .
.
As the simplest observable, the existence observable
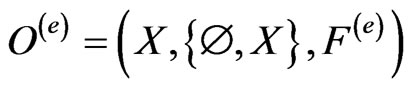 is defined such that
is defined such that 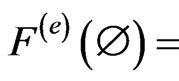 0 and
0 and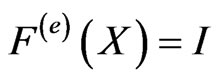 .
.
With anysystem S, a C*-algebra 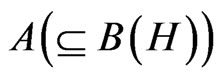 can be associated in which the measurement theory (A) of that system can be formulated. A state of the system S is represented by an element
can be associated in which the measurement theory (A) of that system can be formulated. A state of the system S is represented by an element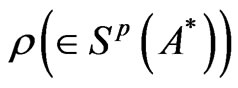 , and an observable is represented by an observable
, and an observable is represented by an observable 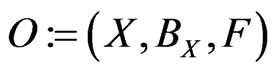 in A. Also, the measurement of the observable O for the system S with the state ρ is denoted by
in A. Also, the measurement of the observable O for the system S with the state ρ is denoted by 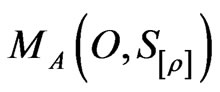 (or more precisely,
(or more precisely,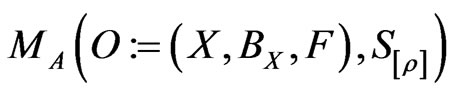 ). An observer can obtain a measured value
). An observer can obtain a measured value 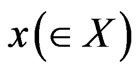 by the measurement
by the measurement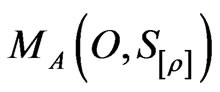 .
.
The axiom presented below is a kind of mathematical generalization of Born’s probabilistic interpretation of quantum mechanics. And thus, it is a statement without reality.
Axiom 1. [Measurement]. The probability that a measured value 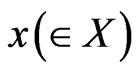 obtained by the measurement
obtained by the measurement
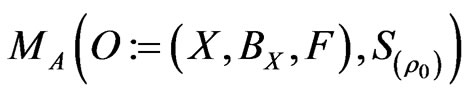 belongs to a set
belongs to a set 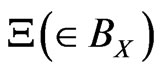 is given by
is given by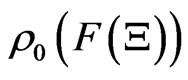 .
.
Next, we explain Axiom 2 in (A). Let (T, ≤) be a tree, i.e., a partial ordered finite set such that “t1 ≤ t3 and t2 ≤ t3” implies “t1 ≤ t2 or t2 ≤ t1”. Assume that there exists an element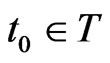 , called the root of T, such that t0 ≤ t (
, called the root of T, such that t0 ≤ t (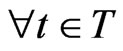 ) holds. Put
) holds. Put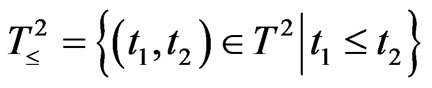 . The family
. The family 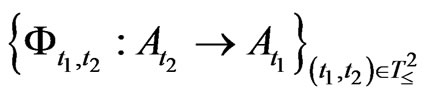 is called a Markov relation (due to the Heisenberg picture), if it satisfies the following conditions 1) and 2).
is called a Markov relation (due to the Heisenberg picture), if it satisfies the following conditions 1) and 2).
1): With each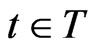 , a C*-algebra At is associated.
, a C*-algebra At is associated.
2): For each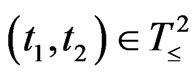 , a Markov operator
, a Markov operator 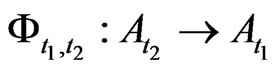 is defined. And it satisfies that
is defined. And it satisfies that
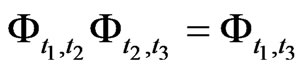 holds for any
holds for any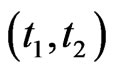 ,
,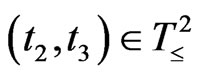 .
.
The family of dual operators 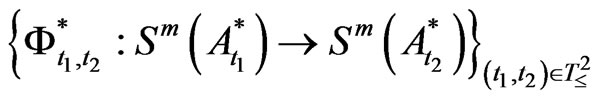 is called a dual Markov relation (due to the Schrödinger picture). However, it is not formally used in measurement theory.
is called a dual Markov relation (due to the Schrödinger picture). However, it is not formally used in measurement theory.
Now Axiom 2 in the measurement theory (A) is presented as follows:
Axiom 2. [Causality]. The causality is represented by a Markov relation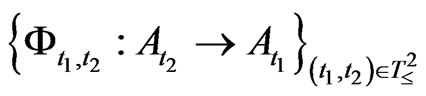 .
.
For the further argument (i.e., the W*-algebraic formulation) of measurement theory, see Appendix in [1].
2.2. Linguistic Interpretation (Figure 1: ②, ③)
The measurement theory (A) asserts
(C): Obey Axioms 1 and 2. And, describe any ordinary phenomenon according to Axioms 1 and 2 (in spite that Axioms 1 and 2 can not be tested experimentally).
Still, most readers may be perplexed how to use Axioms 1 and 2 since there are various usages. Thus, the following problem is significant.
(D): How should Axioms 1 and 2 be used?
Note that reality is not reliable since Axioms 1 and 2 are statements without reality.
Here, in spite of the linguistic turn (Figure 1: ③) and the mathematical generalization from 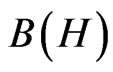 to a C*- algebra A, we consider that the dualism (i.e. the spirit of so called Copenhagen interpretation) of quantum mechanics is inherited to measurement theory (Figure 1: ②). Thus, we present the following interpretation (E) [=(E1) – (E3)]. That is, as the answer to the question (D), we propose:
to a C*- algebra A, we consider that the dualism (i.e. the spirit of so called Copenhagen interpretation) of quantum mechanics is inherited to measurement theory (Figure 1: ②). Thus, we present the following interpretation (E) [=(E1) – (E3)]. That is, as the answer to the question (D), we propose:
(E1) Consider the dualism composed of “observer” and “system (=measuring object)”. And therefore, “observer” and “system” must be absolutely separated.
(E2) Only one measurement is permitted. And thus, the state after a measurement is meaningless since it can not be measured any longer. Also, the causality should be assumed only in the side of system, however, a state never moves. Thus, the Heisenberg picture should be adopted.
(E3) Also, the observer does not have the space-time. Thus, the question: “When and where is a measured value obtained?” is out of measurement theory, and so on.
Although N. Bohr (the chief proponent of the Copenhagen interpretation) said, in the Bohr-Einstein debates [10,11], that the interpretation of a physical theory has to rely on an experimental practice. However, we consider that all confusion is due to the preconception that the Copenhagen interpretation is within physics. In this sense, we agree with A. Einstein, who never accepted the Copenhagen interpretation as physics. That is, in spite of Bohr’s realistic view, as mentioned in [1], we propose the following linguistic world view (Figure 1: ③):
(F) In the beginning was the language called measurement theory (with the interpretation (E)). And, for example, quantum mechanics can be fortunately described in this language. And moreover, almost all scientists have already mastered this language partially and informally since statistics (at least, its basic part) is characterized as one of aspects of measurement theory (cf. [1-6]).
In this sense, we consider that measurement theory holds as a kind of language-game (with the rule (Axioms 1 and 2, Interpretation (E)), and therefore, measurement theory is regarded as the axiomatization (Figure 1: ⑥) of the philosophy of language (i.e. Saussure’s linguistic world view).
3. The Quantum Mechanical World View
In this main section, we shall explain Figure 1: ①-⑧ from the measurement theoretical point of view.
3.1. Realistic World View and Linguistic World View
Figure 1 says that the realistic world view ® and the linguistic world view L exist together in science. Some may ask:
(G): Why is the series L (or, idealism originated by Plato) underestimated in science?
We think that the reason is due to the fact that the L is lacking in the axiomatization ⑥ if we do not have measurement theory. That is, we believe that there is no scientific world view without axiomatization.
3.2. Dualism
Interpretation (E1) says “Image Figure 2 whenever measurement theory is used”. where the interaction [aand b] must not be emphasized, that is, it must be implicit. That is because, if it is explicitly stated, the dualism (E1) is violated.
John Locke’s famous sayings “primary quality (e.g., length, weight, etc.)” and “secondary quality (e.g., sweet, dark, cold, etc.)” urge us to associate the following correspondence:
Also, it may be understandable to regard “observable” as “measurement instrument” or “sensory system”, for example, eyes, glasses, condensation trail (for a plane), etc. And further, it is natural to consider that there is no measured value without observer’s brain (i.e., when something reaches observer’s brain, it becomes a measured value). Thus, we want to consider the following correspondence in Table 1.
In the history of philosophy, two kinds of dualisms (based on “mind-body dualism” and “matter-mind dualism”) may be frequently discussed. However, it should be noted that the dualism (E1) is composed of three concepts as mentioned in Table 1. Also, the following question is nonsense in the linguistic world view.
(H): What is “measured value” (observable, or state)?  Or equivalently, in the sense of Table 1, what is “mind” (body, or matter)?
Or equivalently, in the sense of Table 1, what is “mind” (body, or matter)?  And moreover, what is “probability” (or causality)?
And moreover, what is “probability” (or causality)?
Therefore, we must admit that the correspondence in Table 1 is rather figurative, that is, it is not worth discussing the problem (H) seriously in the linguistic world view. From the great history of philosophy, we learned that the serious consideration (i.e., the consideration from the realistic world view) of the problem (H) (e.g., mindbody problem, etc.) always led us into blind alleys. We have to confirm that we are now in the side of the linguistic world view (i.e., after the linguistic turn ③ in Figure 1) and not the realistic world view. Thus, our interest always focuses on the problem:
(I): How should the term: “measured value” (observable, or state) be used? And moreover, how should the term: “probability” (or causality) beused?
We, of course, assert that this answer is just given by measurement theory (i.e., Axioms 1 and 2, Interpretation (E)). After accepting measurement theory, what we can do in measurement theory is only to trust in man’s linguistic competence. This is our linguistic world view (F). Here, we want to consider that the following two are essentially the same:
(J1) To be is to be perceived (by Berkeley).
(J2) There is no science without measurement (particularly, measured value).
Also, in the sense of Table 1, these are similar to
(J3): There is no science without human’s brain, which may be also similar to Kant’s assertion (see Section 3.7 later). Also, in measurement theory, the (J1) may say that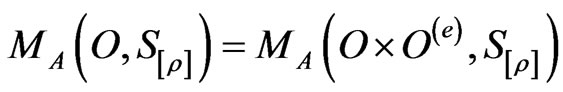 .
.
3.3. I Think, Therefore I Am
Figure 2 (Descartes’ figure in MT) may be inspired from the Descartes primary principle:
(K): I think, therefore I am.
However, it should be noted that this (K) is not a statement in the dualism of Interpretation (E1). That is because it is natural to assume that “I” = “observer” and “I” = “system” in the statement (K), which clearly contradicts the (E1). Thus, we can never expect that the (K) is directly applicable in science. We may see an irony in the fact that the non-dualistic statement (K) gives foundations to the dualistic Figure 2. However, it is sure that the establishment of “I” in (K) brought us modern science (Figure 1: ④).
Also, it is natural to consider that Heidegger’s saying: “In-der-Welt-sein” is out of Figure 2, and thus, out of measure theory. If some succeed the axiomatization of “In-der-Welt-sein”, it will be the powerful rival of measurement theory in science.
3.4. Causality and Probability
The paradigm shift ① in Figure 1 from “purpose (due to Aristotle)” to “causality (due to Bacon, Newton, Hume, etc.) is the greatest paradigm shift throughout all history of science. However, it should be noted that there are several ideas for “causality”. For example Newton’s causality is realistic, and Hume’s causality is subjective. On the other hand, our causality (i.e., Axiom 2) islinguistic.
Although some philosophers (e.g., K. Popper [12]) consider that the discovery of “probability” is as great as that of “causality”, it is sure that the former is underestimated in science, The reason of the underestimation may be due to the fact that the “probability” is never presented in a certain world view (but in mathematics (cf. [13]), on the other hand, the “causality” is established in the world view (i.e., Newtonian mechanics). We think that it is desirable to understand the two concepts (i.e., “probability” and “causality”) in the same world view. It should be noted that this is realized in Axioms 1 and 2 of measurement theory.
3.5. Leibniz-Clarke Correspondence (Space-TimeProblem)
In this section, first we prepare the term “spectrum space”
in the Formula (3). Consider the pair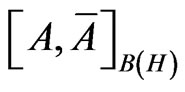 , called a basic structure (cf. Appendix in [1]). Here,
, called a basic structure (cf. Appendix in [1]). Here, 
is a C*-algebra, and 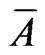 (
(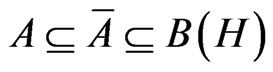 ) is a particular C*-algebra (called a W*-algebra) such that
) is a particular C*-algebra (called a W*-algebra) such that 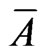 is the weak closure of A in
is the weak closure of A in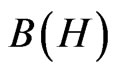 . Let
. Let 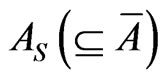 be the commutative C*-subalgebra, which is represented by
be the commutative C*-subalgebra, which is represented by 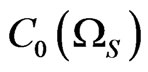 for some locally compact Hausdorff space
for some locally compact Hausdorff space 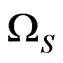 (cf. [7]). The
(cf. [7]). The
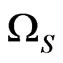 iscalled a spectrum space. For example, consider one particle quantum system, formulated in a basic structure
iscalled a spectrum space. For example, consider one particle quantum system, formulated in a basic structure
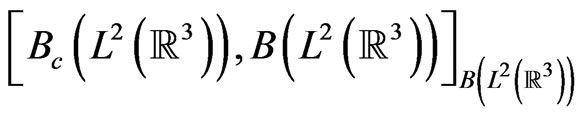 . Then, we can choose the commutative C*-algebra
. Then, we can choose the commutative C*-algebra and thus, we get the spectrum space
and thus, we get the spectrum space . This simple example will make us propose the (M) later.
. This simple example will make us propose the (M) later.
In Leibniz-Clarke correspondence (1715-1716), they (i.e., Leibniz and Clarke (=Newton’s friend)) discussed “space-time problem”. Their ideas are summarized as follows:

That is, Newton considered “What is space-time?”. On the other hand, Leibniz considered “How should the term: space-time be used?” Measurement theory is in Leibniz’s side, and asserts that
(M): Space should be described as a kind of spectrum space. And time should be described as a kind of tree. In other words, time is represented by a parameter t in a linear orderedtree T.
Therefore, we think that the Leibniz-Clarke debates should be essentially regarded as “the linguistic world view 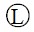 ” vs “the realistic world view ®” in Figure 1. The above (M) should be added to Interpretation (E) as sub-interpretation of measurement theory.
” vs “the realistic world view ®” in Figure 1. The above (M) should be added to Interpretation (E) as sub-interpretation of measurement theory.
3.6. Observer’s Time
It is usual to consider that quantum mechanics and observer’s time are incompatible. This leads Interpretation (E3), which says that observer’s time is nonsense in measurement theory. That is, there is no tense—past, present, future—in measurement theory, and therefore, in science. Many philosophers (e.g., Augustinus, Bergson, Heidegger, etc.) tried to understand observer’s time. However, from the scientific point of view, their attempts may be reckless. From the measurement theoretical point of view, we feel sympathy for J. McTaggart, whose paradox [14] suggests that observer’s time leads science to inconsistency.
3.7. Linguistic Turn (Figure 1: ③, ⑤)
For the question “Which came first, the world or the language?”, two answers (the realistic world view and the linguistic world view) are possible. However, as mentioned in the (F), measurement theory is in the side of “the language came first” (due to Saussure, Wittgenstein, etc.).
Note that two kinds of linguistic turns (i.e., ③ and ⑤) are mentioned in Figure 1. Here, the ③ is the turn from physics to language, and the ⑤ is the turn from “brain” to language. Also, note that the linguistic world view (F) is essentially the same as the following Wittgenstein’s famous statement:
(N) The limits of my language mean the limits of my world.
The interpretation (E3) says that the statement concerning Schrödinger’s cat cannot be described in measurement theory. Therefore, in the sense of the above (N), Schrödinger’s cat (and moreover, Einstein’s world, i.e., the theory of relativity) is out of the world described by measurement theory. This means that Schrödinger’s cat is not paradoxical in the framework of measurement theory. This is the advantage of our linguistic approach to quantum mechanics. Again, see our assertion (F).
Also, the assertion (C) is similar to Kant’s main assertion (“synthetic a priori judgment”) in his famous book “Critique of Pure Reason [15]”, that is, the two are similar in the sense of no experimental validation. Therefore, we want to consider the following correspondence:
(O) [synthetic a priori judgment]  [Axioms 1 and 2]
[Axioms 1 and 2]
However, as mentioned in (J3), Kant’s epistemological approach (i.e., Copernican turn) is rather psychological and not linguistic, in spite that his purpose is philosophy (i.e., the world view) and not psychology (or brain science).
3.8. Parmenides Philosophy
About 2500 years ago, Parmenides said that
(P) There is no “plurality”, but only “one”. And therefore, there is no movement.
We want to regard this (P) as the origin of Interpretation (E2) (i.e., “Only one measurement is permitted. And therefore, a state never moves.”). The (E2), the superiority of the Heisenberg picture to the Schrödinger picture, is the most technical and mathematical interpretation in the (E). And, it is frequently used in the applications of measurement theory (cf. [1-6]). And hence, it is recommended to practice how to use (E2) in [1-6]. At least, see Example 4 in [1].
3.9. Zeno’s Paradoxes
Zeno, the student of Parmenides, proposed several paradoxes concerning movement. The following “Achilles and the tortoise” is most famous.
[Achilles and the tortoise] In a race, the quickest runner can never overtake the slowest, since the pursuer must first reach the point whence the pursued started, so that the slower must always hold a lead.
Beginners of philosophy may have a question:
(Q) Why have philosophers investigated such an easy problem during 2500 years?
However, it should be noted that “Achilles and the tortoise” is not an elementary mathematical problem concerning geometric series. Since Parmenides and Zeno were philosophers, it is natural to consider that Zeno’s paradoxes should be regarded as the problem concerning world view. That is, we believe that Zeno’s question is as follows:
(R) In what kind of world view (in Figure 1) should Zeno’s paradoxes be understood? And further, if the proper world view is not in Figure 1, propose the new world view in which Zeno’s paradoxes can be discussed!
It is clear that Zeno’s paradoxes are not in physics, and thus, Newtonian mechanics, quantum mechanics and the theory of relativity and so on are not proper for the answer to the problem (R). We assert that classical measurement theory is the proper world view, in which Zeno’s paradoxes are described. The classical measurement theoretical description of Zeno’s paradoxes is easy. In fact, it was simply shown in [6].
Readers may be interested in the unnatural situation such that “Achilles” and “tortoise” are quantum particles (i.e., Zeno’s paradoxes in quantum mechanics). Although we have no clear answer to this problem, our paper [16] may be helpful. Also, for the more unnatural situation (i.e., Zeno’s paradoxes in the theory of relativity), see [17].
It is interesting and strange to see that we already have the world description methods (i.e., Newtonian mechanics, quantum mechanics and the theory of relativity) for the unnatural situations, but, we have no world description method for the natural situation if we do not know measurement theory.
3.10. Syllogism
As an example of syllogism, the following example (due to Aristotle) is famous.
(S) Since Socrates is a man and all men are mortal, it follows that Socrates is mortal.
However, it should be noted that there is a great gap between the (S) and the following mathematical syllogism:
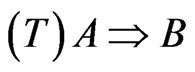 ,
, 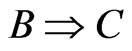 , then, it follows that
, then, it follows that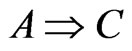 .
.
That is because the (T) is merely mathematical rule and not the world view, and therefore, it is not guaranteed that the rule (T) is applicable to the world (S). In fact, as mentioned in the following section, the (S) does not hold in quantum cases.
Now, we are in the same situation such as (R). That is, we have a similar question (i.e.,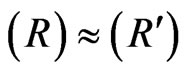 ):
):
(R') In what kind of world view (in Figure 1) should the phenomenon (S) be described? And further, if the proper world view is not in Figure 1, propose the new world view!
We assert that classical measurement theory is the proper world view. In fact, in [2], the above phenomenon (S) is described as a theorem in classical measurement theory.
3.11. Syllogism Does Not Hold in Quantum Systems
Since we understand that EPR-paradox [10] [resp. Bell’s inequality [18]] suggests that quantum mechanics and syllogism [resp. locality] are incompatible, we are not going to assert our originality of the following example. However, in order to promote the understanding of the gap between (S) and (T), let us add a simple and clear example as follows.
Consider the three dimensional Hilbert space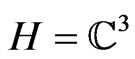 , And therefore, we get the non-commutative C*-algebra
, And therefore, we get the non-commutative C*-algebra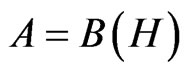 , that is, the algebra composed of all 3 × 3 matrices. Define the three sets such as
, that is, the algebra composed of all 3 × 3 matrices. Define the three sets such as

Here, define the observable 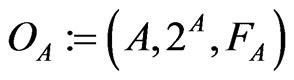 in
in 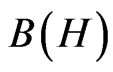 such that
such that
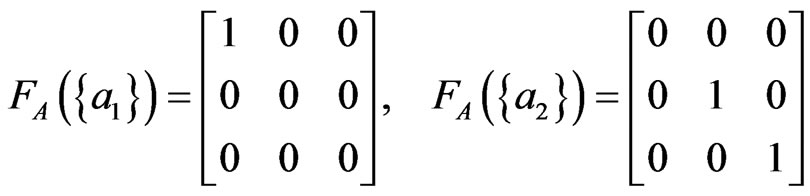 .
.
And define  such that
such that
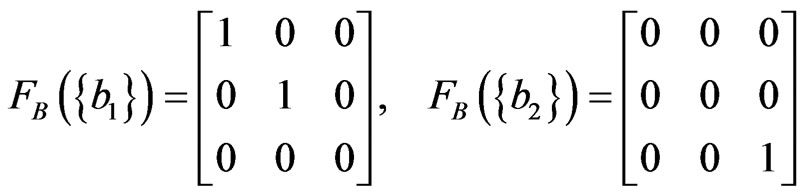 .
.
And further, define  such that
such that
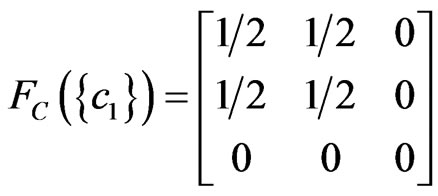 ,
,
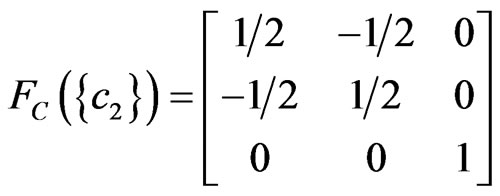 .
.
Define the state 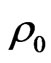 such that
such that
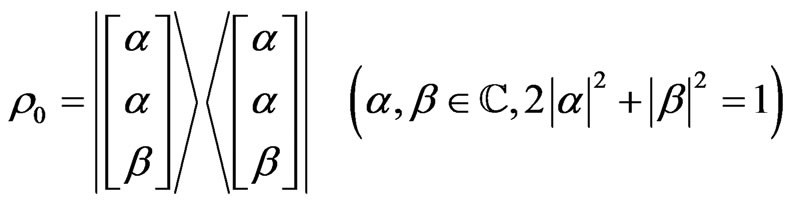 .
.
Since  and
and  [resp.
[resp. 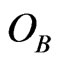 and
and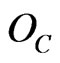 ] commute, we get the product observable
] commute, we get the product observable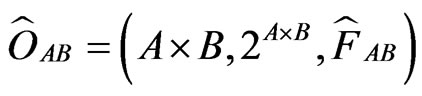 , where
, where

Similarly, we get the product observable
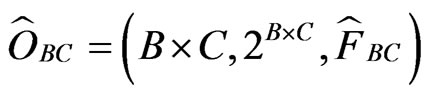 .
.
Here, we see the following (U1) and (U2):
(U1) Let 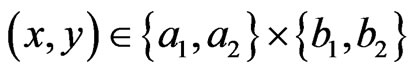 be a measured value obtained by the measurement
be a measured value obtained by the measurement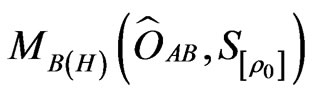 . Then we see:
. Then we see:
 (4)
(4)
since
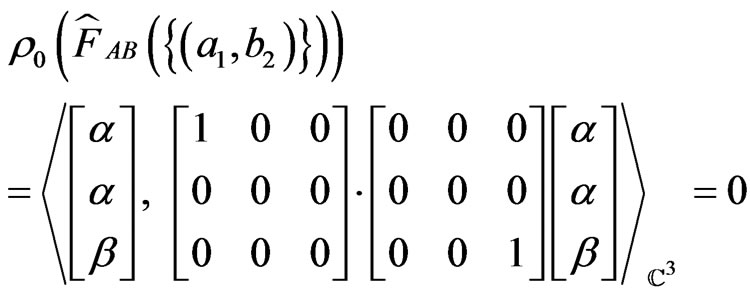 .
.
(U2) Let 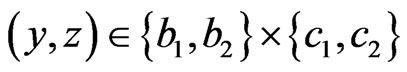 be a measured value obtained by the measurement
be a measured value obtained by the measurement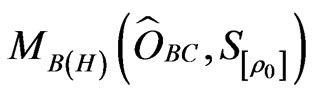 . Then we see:
. Then we see:
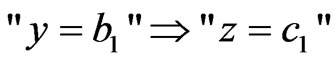 (5)
(5)
since

Thus, some may, from the (4) and (5), conclude that
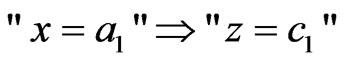 . (6)
. (6)
However, this (6) is wrong. Recall Interpretation (E2), i.e., “only one measurement is permitted”. Thus, we must construct the observable 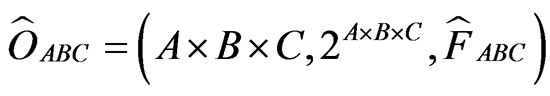 , where
, where

and

And further, we have to take the measurement 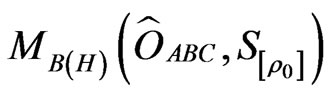 . However, it is easily shown that such observable
. However, it is easily shown that such observable 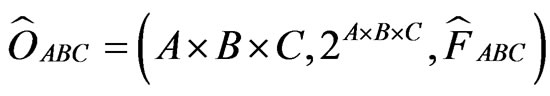 does not exist. Hence, we can conclude that syllogism does not generally hold in quantum measurement theory. We believe that the above argument is essentially the same as that of EPR-paradox [10]. Also, for the precise definition of “implication
does not exist. Hence, we can conclude that syllogism does not generally hold in quantum measurement theory. We believe that the above argument is essentially the same as that of EPR-paradox [10]. Also, for the precise definition of “implication ” in measurement theory, see [2].
” in measurement theory, see [2].
4. Conclusions
As mentioned in [1-6], measurement theory (including several conventional system theories, e.g., statistics, dynamical system theory, quantum system theory, etc.) is one of the most useful theories in science. Following the well-known proverb: “A sound mind in a sound body”, we consider: “A good philosophy in a very useful theory.” For example, “A good realistic philosophy in the theory of relativity” is clearly sure. Therefore, we believe that a good philosophy has to be hidden behind measurement theory. This belief makes us write this paper. And, we want to conclude “A good linguistic philosophy in quantum mechanics (or MT)”.
For example, “A good realistic philosophy in the theory of relativity” is clearly sure. Therefore, we believe that a good philosophy has to be hidden behind measurement theory. This belief makes us write this paper. And, we want to conclude “A good linguistic philosophy in quantum mechanics (or MT)”.
In the abstract of this paper, we promised readers to show a good linguistic philosophy in quantum mechanics. Now we are convinced that this promise is kept. That is because we believe that readers look at the moment philosophy changes to science (Figure 1: ⑧).
Dr. Hawking said in his best seller book [19]: Philosophers reduced the scope of their inquiries so much that Wittgenstein the most famous philosopher this century, said “The sole remaining task for philosophy is the analysis of language.” What a comedown from the great tradition of philosophy from Aristotle to Kant! We think that this is not only his opinion but also most scientists’ opinion. And moreover, we mostly agree with him. However, we believe that it is worth reconsidering the series L (i.e., the linguistic world view) in Figure 1.
Hawking said in his best seller book [19]: Philosophers reduced the scope of their inquiries so much that Wittgenstein the most famous philosopher this century, said “The sole remaining task for philosophy is the analysis of language.” What a comedown from the great tradition of philosophy from Aristotle to Kant! We think that this is not only his opinion but also most scientists’ opinion. And moreover, we mostly agree with him. However, we believe that it is worth reconsidering the series L (i.e., the linguistic world view) in Figure 1.
In this paper, we only studied a few about the relation between quantum mechanics and philosophy. Thus, we hope that our proposal will be discussed and examined from various viewpoints.