Energy Conservation in the Thin Layer Approximation: I. The Spherical Classic Case for Supernovae Remnants

Lorenzo Zaninetti

Physics Department, Turin, Italy.

DOI: 10.4236/ijaa.2020.102006                

Abstract

The thin layer approximation applied to the expansion of a supernova remnant assumes that all the swept mass resides in a thin shell. The law of motion in the thin layer approximation is therefore found using the conservation of momentum. Here we instead introduce the conservation of energy in the framework of the thin layer approximation. The first case to be analysed is that of an interstellar medium with constant density and the second case is that of 7 profiles of decreasing density with respect to the centre of the explosion. The analytical and numerical results are applied to 4 supernova remnants: Tycho, Cas A, Cygnus loop, and SN 1006. The back reaction due to the radiative losses for the law of motion is evaluated in the case of constant density of the interstellar medium.

Keywords

Supernovae: General, Supernovae: Individual (SN Tycho), Supernovae: Individual (SN Cas A), Supernovae: Individual (SN Cygnus Loop), Supernovae: Individual (SN 1006)

1. Introduction

The thin layer approximation assumes that the mass ejected in the explosion of a supernova (SN) resides in a thin layer. This approximation is usually applied in the late stage of the explosion in order to explain the supernova remnant (SNR), see [1] [2] [3]. The physical quantity which is conserved in the previous approaches is the momentum, equal to the swept mass multiplied by the velocity at a given radius of expansion $r_0$ equated to these quantities at a radius r. Some natural questions therefore arise:

· Can we model the expansion of an SNR when the energy is conserved rather than the momentum?

· Can we model the energy conservation when the density of the interstellar medium (ISM) decreases with the distance from the point of the explosion?

In order to answer the above questions, Section 2 reviews the standard laws of conservation, Section 3 introduces the conservation of energy and Section 4 applies the derived equations of motion to 4 SNRs.

2. Laws of Conservation

We summarise four laws of conservation useful to model some astrophysical phenomena in which the temperature and the pressure are absent. The first law is the conservation of momentum in spherical coordinates in the framework of the thin layer approximation. The Newton’s second law for an expanding sphere in the framework of the thin shell approximation along a solid angle $\Delta \Omega$ is

$\frac{\text{d}}{\text{d}t}\left(\frac{1}{3}{r}^3\rho v\right)=r^{2}P\mathrm{,}$ (1)

where r is the advancing radius, $\rho$ is the density assumed to be constant, v the velocity and P the internal pressure, see formula (10.27) in [4]. Let us assume $P=0$ (cold model) and the above equation in two different points of expansion becomes

$M_0\left(r_0\right)v_0=M\left(r\right)v\mathrm{,}$ (2)

where $M_0\left(r_0\right)$ and $M\left(r\right)$ are the swept masses at $r_0$ and r, while $v_0$ and v are the velocities of the thin layer at $r_0$ and r. This first law has been widely used to model the SNRs, see [5] - [10]. This conservation law can be expressed as

a differential equation of the first order by inserting $v=\frac{\text{d}r}{\text{d}t}$ :

$M_0\left(r_0\right)v_0=M\left(r\right)\frac{\text{d}r}{\text{d}t}\mathrm{.}$ (3)

In the case where the ISM has constant density, the analytical solution for the trajectory is

$r\left(t\mathrm{<mo>\; ;\; </mo>}{t}_0\mathrm{,}{r}_0\mathrm{,}{v}_0\right)=\sqrt[4]{4r_0^3{v}_0\left(t-t_0\right)+r_0^4}\mathrm{,}$ (4)

and the velocity is

$v\left(t\mathrm{<mo>\; ;\; </mo>}{t}_0\mathrm{,}{r}_0\mathrm{,}{v}_0\right)=\frac{r_0^3{v}_0}{{\left(4r_0^3{v}_0\left(t-t_0\right)+r_0^4\right)}^{3/4}}\mathrm{,}$ (5)

where $r_0$ and $v_0$ are the position and the velocity when $t=t_0$. The second law is the conservation of energy which will be introduced in details in the next section. An example is given by the energy conserving phase in the interstellar bubbles, see [4]. The third law of conservation is given by the conservation of momentum flux which is the rate of transfer of momentum through a unit area

$\rho \left(x_0\right)v_0^{2}A\left(x_0\right)=\rho \left(x\right)v{\left(x\right)}^{2}A\left(x\right)\mathrm{,}$ (6)

where $\rho \left(x\right)$ is the density at position x, $A\left(x\right)$ is the area at position x and $v\left(x\right)$ is the velocity at position x, see Formula A27 in [11]. This law is useful to model the radiogalaxies where there is a continuous flow of matter from the central region to the periphery, see [12]. The fourth law of conservation is given by the conservation of energy flux which is the rate of transfer of energy through a unit area

$\frac{1}{2}\rho \left(x_0\right)v_0^{3}A\left(x_0\right)=\frac{1}{2}\rho \left(x\right)v{\left(x\right)}^{3}A\left(x\right)$ (7)

where $\rho \left(x\right)$ is the density at position x, $A\left(x\right)$ is the area at position x and $v\left(x\right)$ is the velocity at position x, see Formula A28 in [11]. This law is useful to model the astrophysical jets, see [13].

3. Energy Conservation

The conservation of kinetic energy in spherical coordinates within the framework of the thin layer approximation when the thermal effects are negligible is

$\frac{1}{2}{M}_0\left(r_0\right)v_0^2=\frac{1}{2}M\left(r\right)v^2\mathrm{,}$ (8)

where $M_0\left(r_0\right)$ and $M\left(r\right)$ are the swept masses at $r_0$ and r, while $v_0$ and v are the velocities of the thin layer at $r_0$ and r. The above conservation law, when written as a differential equation, is

$\frac{1}{2}M\left(r\right){\left(\frac{\text{d}}{\text{d}t}r\left(t\right)\right)}^2-\frac{1}{2}{M}_0{v}_0^2=0.$ (9)

The velocity as a function of the momentary radius is

$v\left(r\mathrm{<mo>\; ;\; </mo>}{r}_0\mathrm{,}{v}_0\right)=\frac{r_0^{3/2}{v}_0}{r^{3/2}}\mathrm{.}$ (10)

In the following, the case of constant density as well as 7 profiles of decreasing density will be considered.

3.1. Medium with Constant Density

When the ISM is considered to have constant density, the analytical solution for the trajectory when the energy is conserved is

$r\left(t\mathrm{<mo>\; ;\; </mo>}{t}_0\mathrm{,}{r}_0\mathrm{,}{v}_0\right)=\frac{1}{2}{2}^{3/5}{r}_0^{3/5}{\left(\left(5t-5t_0\right)v_0+2r_0\right)}^{2/5}\mathrm{,}$ (11)

which has the asymptotic behaviour $r_a\left(t\mathrm{<mo>\; ;\; </mo>}{t}_0\mathrm{,}{r}_0\mathrm{,}{v}_0\right)$,

$r_a\left(t\mathrm{<mo>\; ;\; </mo>}{t}_0\mathrm{,}{r}_0\mathrm{,}{v}_0\right)~\frac{1}{2}\frac{2^{3/5}{r}_0^{3/5}{5}^{2/5}{v}_0^{2/5}}{{\left(t^{-1}\right)}^{2/5}}+\frac{1}{25}\frac{2^{3/5}{r}_0^{3/5}{5}^{2/5}\left(-5t_0{v}_0+2r_0\right){\left(t^{-1}\right)}^{3/5}}{v_0^{3/5}}\mathrm{.}$ (12)

The velocity as function of the radius is

$v\left(r\mathrm{<mo>\; ;\; </mo>}{r}_0\mathrm{,}{v}_0\right)=\frac{r_0^{3/2}{v}_0}{r^{3/2}}\mathrm{,}$ (13)

and the velocity as a function of time is

$v\left(t\mathrm{<mo>\; ;\; </mo>}{t}_0\mathrm{,}{r}_0\mathrm{,}{v}_0\right)=\frac{2^{3/5}{r}_0^{3/5}{v}_0}{{\left(\left(5t-5t_0\right)v_0+2r_0\right)}^{3/5}}\mathrm{,}$ (14)

where $r_0$ and $v_0$ are the position and the velocity when $t=t_0$.

3.2. Constant Density and Back Reaction

The radiative losses per unit length are assumed to be proportional to the flux of momentum

$-ϵ{\rho }_s{v}^{2}4\pi r^2\mathrm{,}$ (15)

where $ϵ$ is a constant and $rh{o}_s$ is density in the thin advancing layer which is $4\rho$. Inserting in the above equation the velocity to first order as given by Equation (13) the radiative losses, $Q\mathrm{<mo\; stretchy="false">\; (\; </mo>}r\mathrm{<mo>\; ;\; </mo>}{r}_0\mathrm{,}{v}_0\mathrm{,}\epsilon \mathrm{<mo\; stretchy="false">\; )\; </mo>}$, are

$Q\left(r\mathrm{<mo>\; ;\; </mo>}{r}_0\mathrm{,}{v}_0\mathrm{,}ϵ\right)=-16\frac{ϵ\rho r_0^3{v}_0^2\pi }{r}\mathrm{.}$ (16)

The sum of the radiative losses between $r_0$ and r is given by the following integral, L,

$\begin{array}{c}L\left(r\mathrm{<mo>\; ;\; </mo>}{r}_0\mathrm{,}{v}_0\mathrm{,}ϵ\right)={\displaystyle {\int }_{r_0}^r}Q\left(r\mathrm{<mo>\; ;\; </mo>}{r}_0\mathrm{,}{v}_0\mathrm{,}ϵ\right)\text{d}r\\ =-16ϵ\rho r_0^3{v}_0^2\pi ln\left(r\right)+16ϵ\rho r_0^3{v}_0^2\pi ln\left(r_0\right)\mathrm{.}\end{array}$ (17)

The conservation of energy in presence of the back reaction due to the radiative losses is

$2/3\rho \pi r^3{v}^2+16ϵ\rho r_0^3{v}_0^2\pi ln\left(r\right)-16ϵ\rho r_0^3{v}_0^2\pi ln\left(r_0\right)=2/3\rho \pi r_0^3{v}_0^2\mathrm{.}$ (18)

The analytical solution for the velocity to second order, $v_c\left(r\mathrm{<mo>\; ;\; </mo>}{r}_0\mathrm{,}{c}_0\mathrm{,}ϵ\right)$, is

$v_c\left(r\mathrm{<mo>\; ;\; </mo>}{r}_0\mathrm{,}{v}_0\mathrm{,}ϵ\right)=\frac{r_0^{3/2}\sqrt{-24ln\left(r\right)ϵ+24ln\left(r_0\right)ϵ+1}{v}_0}{r^{3/2}}\mathrm{.}$ (19)

The inclusion of back reaction allows the evaluation of the SRS’s maximum length $r_{back}\left(r_0\mathrm{,}ϵ\right)$, which can be derived imposing to zero the above velocity.

$r_{back}\left(r_0\mathrm{,}ϵ\right)={\text{e}}^{1/24\frac{24ln\left(r_0\right)ϵ+1}{ϵ}}\mathrm{.}$ (20)

3.3. Medium with an Hyperbolic Profile of Density

We assume that the medium around the SN scales with the piecewise dependence

$\rho \left(r\mathrm{<mo>\; ;\; </mo>}{r}_0\right)=\{\begin{array}{ll}{\rho }_c\hfill & \text{if}r\le r_0\hfill \\ {\rho }_c\left(\frac{r_0}{r}\right)\hfill & \text{if}r>r_0\hfill \end{array}$ (21)

where ${\rho }_c$ is the density at $r=0$ and $r_0$ is the radius after which the density starts to decrease. The mass swept, $M_0$, in the interval $\left[0,r_0\right]$ is

$M_0\left({\rho }_c\mathrm{,}{r}_0\right)=\frac{4}{3}{\rho }_c\pi r_0^3\mathrm{.}$

The total mass swept, $M\left(r\mathrm{<mo>\; ;\; </mo>}{r}_0\mathrm{,}{\rho }_c\right)$, in the interval $\left[0,r\right]$ is

$M\left(r\mathrm{<mo>\; ;\; </mo>}{r}_0\mathrm{,}{\rho }_c\right)=-\frac{2}{3}{\rho }_c\pi r_0^3+2{\rho }_c{r}_0{r}^2\pi \mathrm{.}$

The application of energy conservation gives the velocity as a function of the radius:

$v\left(r\mathrm{<mo>\; ;\; </mo>}{r}_0\mathrm{,}{v}_0\right)=2\frac{v_0{r}_0}{\sqrt{6r^2-2r_0^2}}\mathrm{.}$ (22)

Separation of variables followed by integration gives

$\begin{array}{l}\frac{1}{12}\frac{r_0\sqrt{6}ln\left(\sqrt{2}+\sqrt{3}\right)}{v_0}-\frac{1}{12}\frac{r_0\sqrt{6}ln\left(r\sqrt{2}\sqrt{3}+\sqrt{6r^2-2r_0^2}\right)}{v_0}\\ +\frac{1}{24}\frac{r_0\sqrt{6}ln\left(2\right)}{v_0}+\frac{1}{12}\frac{r_0\sqrt{6}ln\left(r_0\right)}{v_0}+\frac{1}{4}\frac{r\sqrt{6r^2-2r_0^2}}{v_0{r}_0}-\frac{1}{2}\frac{r_0}{v_0}=t-t_0\mathrm{.}\end{array}$ (23)

In this equation it is not possible to extract the radius as a function of time, and therefore a numerical procedure is adopted in order to derive the trajectory.

3.4. Medium with an Inverse Square Profile for the Density

We now assume that the medium around the SN scales with the piecewise dependence (which avoids a pole at $r=0$ )

$\rho \left(r\mathrm{<mo>\; ;\; </mo>}{r}_0\right)=\{\begin{array}{ll}{\rho }_c\hfill & \text{if}r\le r_0\hfill \\ {\rho }_c{\left(\frac{r_0}{r}\right)}^2\hfill & \text{if}r>r_0\hfill \end{array}$ (24)

where ${\rho }_c$ is the density at $r=0$ and $r_0$ is the radius after which the density starts to decrease.

The total mass swept, $M\left(r\mathrm{<mo>\; ;\; </mo>}{r}_0\mathrm{,}{\rho }_c\right)$, in the interval $\left[0,r\right]$ is

$M\left(r\mathrm{<mo>\; ;\; </mo>}{r}_0\mathrm{,}{\rho }_c\right)=-\frac{8}{3}{\rho }_c\pi r_0^3+4{\rho }_c{r}_0^2\pi r+\frac{4}{3}{\rho }_c\pi r_0^3\mathrm{.}$

Applying the conservation of energy, the velocity as a function of the radius is

$v\left(r\mathrm{<mo>\; ;\; </mo>}{r}_0\mathrm{,}{v}_0\right)=-\frac{\sqrt{-\left(2r_0-3r\right)r_0}{v}_0}{2r_0-3r}\mathrm{.}$ (25)

The trajectory, i.e. the radius as a function of time, is

$r\left(t\mathrm{<mo>\; ;\; </mo>}{t}_0\mathrm{,}{r}_0\mathrm{,}{v}_0\right)=\frac{1}{6}\sqrt[3]{2}\sqrt[3]{r_0}{\left(\left(9t-9t_0\right)v_0+2r_0\right)}^{2/3}+\frac{2}{3}{r}_0\mathrm{,}$ (26)

which has the asymptotic behavior, $r_a\left(t\mathrm{<mo>\; ;\; </mo>}{t}_0\mathrm{,}{r}_0\mathrm{,}{v}_0\right)$,

$r_a\left(t\mathrm{<mo>\; ;\; </mo>}{t}_0\mathrm{,}{r}_0\mathrm{,}{v}_0\right)~\frac{1}{6}\frac{\sqrt[3]{2}\sqrt[3]{r_0}{9}^{2/3}{v}_0^{2/3}}{{\left(t^{-1}\right)}^{2/3}}+\frac{2}{3}{r}_0+\frac{\sqrt[3]{2}\sqrt[3]{r_0}{9}^{2/3}\left(-9t_0{v}_0+2r_0\right)\sqrt[3]{t^{-1}}}{81\sqrt[3]{v_0}}\mathrm{.}$ (27)

The velocity as a function of time is

$v\left(t\mathrm{<mo>\; ;\; </mo>}{t}_0\mathrm{,}{r}_0\mathrm{,}{v}_0\right)=\frac{\sqrt[3]{2}\sqrt[3]{r_0}{v}_0}{\sqrt[3]{\left(9t-9t_0\right)v_0+2r_0}}\mathrm{.}$ (28)

3.5. Medium with a Power Law Profile for the Density

We now assume that the medium around the SN scales as

$\rho \left(r\mathrm{<mo>\; ;\; </mo>}{r}_0\right)=\{\begin{array}{ll}{\rho }_c\hfill & \text{if}r\le r_0\hfill \\ {\rho }_c{\left(\frac{r_0}{r}\right)}^{\alpha }\hfill & \text{if}r>r_0\hfill \end{array}$ (29)

where ${\rho }_c$ is the density at $r=0$, $r_0$ is the radius after which the density starts to decrease and $\alpha >0$.

The total mass swept, $M\left(r\mathrm{<mo>\; ;\; </mo>}{r}_0\mathrm{,}{\rho }_c\mathrm{,}\alpha \right)$, in the interval $\left[0,r\right]$ is

$M\left(r\mathrm{<mo>\; ;\; </mo>}{r}_0\mathrm{,}{\rho }_c\mathrm{,}\alpha \right)=\frac{4}{3}{\rho }_c\pi r_0^3-4\frac{r^3{\rho }_c\pi }{\alpha -3}{\left(\frac{r_0}{r}\right)}^{\alpha }+4\frac{{\rho }_c\pi r_0^3}{\alpha -3}\mathrm{.}$

The application of energy conservation gives the differential equation

$\frac{1}{3\alpha -9}\left(-2{\rho }_c\pi \left(3r^3{\left(\frac{r_0}{r}\right)}^{\alpha }-r_0^3\alpha \right){\left(\frac{\text{d}}{\text{d}t}r\left(t\right)\right)}^2\right)=\frac{2}{3}{\rho }_c\pi r_0^3{v}_0^2\mathrm{.}$ (30)

The velocity as a function of the radius is

$v\left(r\mathrm{<mo>\; ;\; </mo>}{r}_0\mathrm{,}{v}_0\mathrm{,}\alpha \right)=\frac{\sqrt{-\left(-r_0^3\alpha +3r^{3-\alpha }{r}_0^{\alpha }\right)r_0\left(\alpha -3\right)}{v}_0{r}_0}{-r_0^3\alpha +3r^{3-\alpha }{r}_0^{\alpha }}\mathrm{.}$ (31)

There is no analytical solution for the trajectory, and therefore we have implemented a numerical procedure. The first approximation for the trajectory is obtained by a series solution of Equation (30) to fourth order,

$r\left(t\mathrm{<mo>\; ;\; </mo>}{r}_0\mathrm{,}{v}_0\mathrm{,}{t}_0\mathrm{,}\alpha \right)\approx r_0+v_0\left(t-t_0\right)-\frac{3}{4}\frac{v_0^2{\left(t-t_0\right)}^2}{r_0}+\frac{1}{4}\frac{v_0^3\left(\alpha +4\right){\left(t-t_0\right)}^3}{r_0^2}\mathrm{.}$ (32)

The second approximation for the trajectory is found by first deriving an asymptotic expansion of Equation (31), namely

$v\left(r\mathrm{<mo>\; ;\; </mo>}{r}_0\mathrm{,}{v}_0\mathrm{,}\alpha \right)~\frac{1}{3}\frac{v_0{r}_0\sqrt{3}\sqrt{r_0^{\alpha +1}\left(3-\alpha \right)}}{r_0^{\alpha }\sqrt{{\left(r^{-1}\right)}^{\alpha -3}}}\mathrm{.}$ (33)

Then, the asymptotic approximate trajectory turns out to be

$\begin{array}{l}r\left(t\mathrm{<mo>\; ;\; </mo>}{r}_0\mathrm{,}{v}_0\mathrm{,}{t}_0\mathrm{,}\alpha \right)~{12}^{{\left(\alpha -5\right)}^{-1}}{r}_0^{\frac{\alpha -3}{\alpha -5}}\times (-4r_0{v}_0\left(\alpha -5\right)\left(t-t_0\right)\sqrt{9-3\alpha }\\ -{\left(\alpha -3\right){\left(\alpha -5\right)}^2{\left(t-t_0\right)}^2{v}_0^2+12r_0^2)}^{-{\left(\alpha -5\right)}^{-1}}\mathrm{.}\end{array}$ (34)

3.6. Medium with an Exponential Profile for the Density

We assume that the medium around the SN scales with the piecewise dependence

$\rho \left(r;r_0\right)=\{\begin{array}{ll}{\rho }_c\hfill & \text{if}r\le r_0\hfill \\ {\rho }_c\left(\exp -\frac{r}{b}\right)\hfill & \text{if}r>r_0\hfill \end{array}$ (35)

where ${\rho }_c$ is the density at $r=0$ and $r_0$ is the radius after which the density starts to decrease. The total mass swept, $M\left(r\mathrm{<mo>\; ;\; </mo>}{r}_0\mathrm{,}{\rho }_c\right)$, in the interval $\left[0,r\right]$ is

$\begin{array}{c}M\left(r\mathrm{<mo>\; ;\; </mo>}{r}_0\mathrm{,}{\rho }_c\mathrm{,}b\right)=\frac{4}{3}{\rho }_c\pi r_0^3-4b\left(2b^2+2br+r^2\right){\rho }_c{\text{e}}^{-\frac{r}{b}}\pi \\ +4b\left(2b^2+2b{r}_0+r_0^2\right){\rho }_c{\text{e}}^{-\frac{r_0}{b}}\pi \mathrm{.}\end{array}$

The application of energy conservation gives the differential equation

$\begin{array}{l}-2{\left(\frac{\text{d}}{\text{d}t}r\left(t\right)\right)}^2{\rho }_c(6b^3{\text{e}}^{-\frac{r}{b}}+6b^{2}r{\text{e}}^{-\frac{r}{b}}+3b{r}^2{\text{e}}^{-\frac{r}{b}}-6b^3{\text{e}}^{-\frac{r_0}{b}}\\ -6b^2{\text{e}}^{-\frac{r_0}{b}}{r}_0-3b{\text{e}}^{-\frac{r_0}{b}}{r}_0^2-r_0^3)\pi =\frac{2}{3}{\rho }_c\pi r_0^3{v}_0^2\mathrm{.}\end{array}$ (36)

The velocity as a function of the radius is

$v\left(r\mathrm{<mo>\; ;\; </mo>}{r}_0\mathrm{,}{v}_0\mathrm{,}b\right)=\frac{N}{D}\mathrm{,}$ (37)

where

$N=-\sqrt{-6r_0\left(\left(-b^3-b^2{r}_0-\frac{1}{2}b{r}_0^2\right){\text{e}}^{-\frac{r_0}{b}}+b\left(b^2+br+\frac{1}{2}{r}^2\right){\text{e}}^{-\frac{r}{b}}-1/6r_0^3\right)}{v}_0{r}_0\mathrm{,}$ (38)

and

$D=\left(-6b^3-6b^2{r}_0-3b{r}_0^2\right){\text{e}}^{-\frac{r_0}{b}}+\left(6b^3+6b^{2}r+3b{r}^2\right){\text{e}}^{-\frac{r}{b}}-r_0^3\mathrm{.}$ (39)

There is no analytical solution for the trajectory, and therefore we present a series solution of Equation (36) to fourth order:

$\begin{array}{c}r\left(t\mathrm{<mo>\; ;\; </mo>}{r}_0\mathrm{,}{v}_0\mathrm{,}{t}_0\mathrm{,}b\right)\approx r_0+\left(t-t_0\right)v_0-\frac{3}{4}\frac{v_0^2{\left(t-t_0\right)}^2}{r_0}{\text{e}}^{-\frac{r_0}{b}}\\ +\frac{1}{4}\frac{v_0^3{\left(t-t_0\right)}^3}{b{r}_0^2}{\text{e}}^{-\frac{r_0}{b}}\left(6b{\text{e}}^{-\frac{r_0}{b}}-2b+r_0\right)\mathrm{.}\end{array}$ (40)

3.7. Medium with a Gaussian Profile for the Density

We assume that the medium around the SN scales with the piecewise dependence

$\rho \left(r;r_0,b\right)=\{\begin{array}{ll}{\rho }_c\hfill & \text{if}r\le r_0\hfill \\ {\rho }_c\left(\exp -{\left(\frac{r}{b}\right)}^2\right)\hfill & \text{if}r>r_0\hfill \end{array}$ (41)

where ${\rho }_c$ is the density at $r=0$ and $r_0$ is the radius after which the density starts to decrease. The total mass swept, $M\left(r\mathrm{<mo>\; ;\; </mo>}{r}_0\mathrm{,}{\rho }_c\right)$, in the interval $\left[0,r\right]$ is

$\begin{array}{c}M\left(r;r_0,{\rho }_c,b\right)=\frac{4}{3}{\rho }_c\pi r_0^3+4{\rho }_c\pi \left(-\frac{1}{2}{\text{e}}^{-\frac{r^2}{b^2}}r{b}^2+\frac{1}{4}{b}^3\sqrt{\pi }\text{erf}\left(\frac{r}{b}\right)\right)\\ -4{\rho }_c\pi \left(-\frac{1}{2}{\text{e}}^{-\frac{r_0^2}{b^2}}{r}_0{b}^2+\frac{1}{4}{b}^3\sqrt{\pi }\text{erf}\left(\frac{r_0}{b}\right)\right),\end{array}$ (42)

where $\text{erf}\left(x\right)$ is the error function, defined by

$\text{erf}\left(x\right)=\frac{2}{\sqrt{\pi }}{\displaystyle {\int }_0^x}{\text{e}}^{-t^2}\text{d}t\mathrm{,}$ (43)

See [14].

The differential equation when the energy is conserved is

$\begin{array}{l}-\frac{1}{6}{\left(\frac{\text{d}}{\text{d}t}r\left(t\right)\right)}^2\pi {\rho }_c(-3b^3\sqrt{\pi }\text{erf}\left(\frac{r\left(t\right)}{b}\right)+3b^3\sqrt{\pi }\text{erf}\left(\frac{r_0}{b}\right)\begin{array}{c}\\ \\ \end{array}\\ +6{\text{e}}^{-\frac{{\left(r\left(t\right)\right)}^2}{b^2}}r\left(t\right)b^2-6{\text{e}}^{-\frac{r_0^2}{b^2}}{r}_0{b}^2-4r_0^3)\mathrm{<mo>\; =\; </mo>}\frac{2}{3}{\rho }_c\pi r_0^3{v}_0^2\mathrm{.}\end{array}$ (44)

In the absence of an analytical solution for this differential equation, we present an approximation using the fourth order Taylor series:

$\begin{array}{c}r\left(t\mathrm{<mo>\; ;\; </mo>}{r}_0\mathrm{,}{v}_0\mathrm{,}{t}_0\mathrm{,}b\right)\approx r_0+v_0\left(t-t_0\right)-\frac{3}{4}\frac{v_0^2{\left(t-t_0\right)}^2}{r_0}{\text{e}}^{-\frac{r_0^2}{b^2}}\\ +\frac{1}{2}\frac{v_0^3{\left(t-t_0\right)}^3}{r_0^2{b}^2}{\text{e}}^{-\frac{r_0^2}{b^2}}\left(3b^2{\text{e}}^{-\frac{r_0^2}{b^2}}-b^2+r_0^2\right)\mathrm{.}\end{array}$ (45)

3.8. Autogravitating Medium

We assume that the medium around the SN scales with the piecewise dependence

$\rho \left(r;r_0,b\right)=\{\begin{array}{ll}{\rho }_c\hfill & \text{if}r\le r_0\hfill \\ {\rho }_c\left({\text{sech}}^2\left(\frac{r}{2b}\right)\right)\hfill & \text{if}r>r_0\hfill \end{array}$ (46)

where ${\rho }_c$ is the density at $r=0$, $r_0$ is the radius after which the density starts to decrease and sech is the hyperbolic secant ( [15] [16] [17] [18]).

The total mass swept, $M\left(r\mathrm{<mo>\; ;\; </mo>}{r}_0\mathrm{,}b\mathrm{,}{\rho }_c\right)$, in the interval $\left[0,r\right]$ is

$\begin{array}{l}M\left(r\mathrm{<mo>\; ;\; </mo>}{r}_0\mathrm{,}{\rho }_c\mathrm{,}b\right)\\ =\frac{4}{3}{\rho }_c\pi r_0^3-16{\rho }_c\pi r^{2}b{\left(1+{\text{e}}^{\frac{r}{b}}\right)}^{-1}-32{\rho }_c\pi b^{2}rln\left(1+{\text{e}}^{\frac{r}{b}}\right)\\ -32{\rho }_c\pi b^{3}polylog\left(\mathrm{2,}-{\text{e}}^{\frac{r}{b}}\right)+16{\rho }_c\pi r^{2}b+16{\rho }_c\pi r_0^{2}b{\left(1+{\text{e}}^{\frac{r_0}{b}}\right)}^{-1}\\ +32{\rho }_c\pi b^2{r}_{0}ln\left(1+{\text{e}}^{\frac{r_0}{b}}\right)+32{\rho }_c\pi b^{3}polylog\left(\mathrm{2,}-{\text{e}}^{\frac{r_0}{b}}\right)-16{\rho }_c\pi r_0^{2}b\mathrm{,}\end{array}$ (47)

where the polylog operator is defined by

$polylog\left(s\mathrm{,}z\right)={\text{Li}}_s\left(z\right)={\displaystyle \underset{n=1}{\overset{\infty }{\sum }}}\frac{z^n}{n^s}$ (48)

and ${\text{Li}}_s\left(z\right)$ is a Dirichlet series. The differential equation when the energy is conserved is

$\frac{ODEN}{3\left(1+{\text{e}}^{\frac{r\left(t\right)}{b}}\right)\left(1+{\text{e}}^{\frac{r_0}{b}}\right)}=\frac{2}{3}{\rho }_c\pi r_0^3{v}_0^2$ (49)

where

$\begin{array}{c}ODEN=48{\left(\frac{\text{d}}{\text{d}t}r\left(t\right)\right)}^2(-b^3\left({\text{e}}^{\frac{r\left(t\right)+r_0}{b}}+{\text{e}}^{\frac{r_0}{b}}+{\text{e}}^{\frac{r\left(t\right)}{b}}+1\right)polylog\left(\mathrm{2,}-{\text{e}}^{\frac{r\left(t\right)}{b}}\right)\\ +(-b^{2}r\left(t\right)ln\left(1+{\text{e}}^{\frac{r\left(t\right)}{b}}\right)+b^{3}polylog\left(\mathrm{2,}-{\text{e}}^{\frac{r_0}{b}}\right)+b^2{r}_{0}ln\left(1+{\text{e}}^{\frac{r_0}{b}}\right)\\ +\frac{1}{2}{\left(r\left(t\right)\right)}^{2}b-\frac{1}{2}{r}_0^2\left(b-\frac{1}{12}{r}_0\right)){\text{e}}^{\frac{r\left(t\right)+r_0}{b}}-b^{2}r\left(t\right)\left({\text{e}}^{\frac{r_0}{b}}+{\text{e}}^{\frac{r\left(t\right)}{b}}+1\right)ln\left(1+{\text{e}}^{\frac{r\left(t\right)}{b}}\right)\\ +b^3\left({\text{e}}^{\frac{r_0}{b}}+{\text{e}}^{\frac{r\left(t\right)}{b}}+1\right)polylog\left(\mathrm{2,}-{\text{e}}^{\frac{r_0}{b}}\right)+b^2{r}_0\left({\text{e}}^{\frac{r_0}{b}}+{\text{e}}^{\frac{r\left(t\right)}{b}}+1\right)ln\left(1+{\text{e}}^{\frac{r_0}{b}}\right)\\ +\left(\frac{1}{2}{\left(r\left(t\right)\right)}^{2}b+1/24r_0^3\right){\text{e}}^{\frac{r\left(t\right)}{b}}-1/2r_0^2\left(\left(b-\frac{1}{12}{r}_0\right){\text{e}}^{\frac{r_0}{b}}-\frac{1}{12}{r}_0\right)){\rho }_c\pi \mathrm{.}\end{array}$ (50)

The velocity as a function of the radius is

$v\left(r\mathrm{<mo>\; ;\; </mo>}{r}_0\mathrm{,}b\right)=\frac{r_0^{\frac{3}{2}}\sqrt{{\text{e}}^{\frac{r_0+r}{b}}+{\text{e}}^{\frac{r_0}{b}}+{\text{e}}^{\frac{r}{b}}+1}{v}_0}{VELD}$ (51)

where

$\begin{array}{c}VELD=(24b^{3}polylog\left(\mathrm{2,}-{\text{e}}^{\frac{r_0}{b}}\right){\text{e}}^{\frac{r_0+r}{b}}+24b^3{\text{e}}^{\frac{r}{b}}polylog\left(\mathrm{2,}-{\text{e}}^{\frac{r_0}{b}}\right)\\ +24b^3{\text{e}}^{\frac{r_0}{b}}polylog\left(\mathrm{2,}-{\text{e}}^{\frac{r_0}{b}}\right)-24b^{3}polylog\left(\mathrm{2,}-{\text{e}}^{\frac{r}{b}}\right){\text{e}}^{\frac{r_0+r}{b}}\\ -24b^3{\text{e}}^{\frac{r}{b}}polylog\left(\mathrm{2,}-{\text{e}}^{\frac{r}{b}}\right)-24b^3{\text{e}}^{\frac{r_0}{b}}polylog\left(\mathrm{2,}-{\text{e}}^{\frac{r}{b}}\right)\\ +24ln\left(1+{\text{e}}^{\frac{r_0}{b}}\right){\text{e}}^{\frac{r_0+r}{b}}{b}^2{r}_0+24b^2{r}_0{\text{e}}^{\frac{r}{b}}ln\left(1+{\text{e}}^{\frac{r_0}{b}}\right)\end{array}$

$\begin{array}{l}+24b^2{r}_0{\text{e}}^{\frac{r_0}{b}}ln\left(1+{\text{e}}^{\frac{r_0}{b}}\right)-24ln\left(1+{\text{e}}^{\frac{r}{b}}\right){\text{e}}^{\frac{r_0+r}{b}}{b}^{2}r-24b^{2}r{\text{e}}^{\frac{r}{b}}ln\left(1+{\text{e}}^{\frac{r}{b}}\right)\\ +24b^2{r}_{0}ln\left(1+{\text{e}}^{\frac{r_0}{b}}\right)-24b^{2}r{\text{e}}^{\frac{r_0}{b}}ln\left(1+{\text{e}}^{\frac{r}{b}}\right)+24b^{3}polylog\left(\mathrm{2,}-{\text{e}}^{\frac{r_0}{b}}\right)\\ -24b^{3}polylog\left(\mathrm{2,}-{\text{e}}^{\frac{r}{b}}\right)-24b^{2}rln\left(1+{\text{e}}^{\frac{r}{b}}\right)+12{\text{e}}^{\frac{r_0+r}{b}}b{r}^2-12{\text{e}}^{\frac{r_0+r}{b}}b{r}_0^2\\ +{\text{e}}^{\frac{r_0+r}{b}}{r}_0^3+12b{r}^2{\text{e}}^{\frac{r}{b}}+{r_0^3{\text{e}}^{\frac{r}{b}}-12b{r}_0^2{\text{e}}^{\frac{r_0}{b}}+r_0^3{\text{e}}^{\frac{r_0}{b}}+r_0^3)}^{1/2}\mathrm{.}\end{array}$ (52)

In the absence of an analytical solution for this differential equation, we present the approximation arising from the fourth order Taylor series:

$\begin{array}{l}r\left(t\mathrm{<mo>\; ;\; </mo>}{r}_0\mathrm{,}{v}_0\mathrm{,}{t}_0\mathrm{,}b\right)\approx r_0+v_0\left(t-t_0\right)\\ +3\frac{v_0^2{\left(t-t_0\right)}^2}{r_0^2}\left(2{\left({\text{e}}^{\frac{r_0}{b}}\right)}^{2}b-{\left({\text{e}}^{\frac{r_0}{b}}\right)}^2{r}_0-{\text{e}}^{\frac{r_0}{b}}{r}_0-2b{\text{e}}^{2\frac{r_0}{b}}\right)\\ \times {\left(1+{\text{e}}^{\frac{r_0}{b}}\right)}^{-1}{\left({\text{e}}^{2\frac{r_0}{b}}+2{\text{e}}^{\frac{r_0}{b}}+1\right)}^{-1}\\ +\frac{v_0^3{\left(t-t_0\right)}^3}{r_0^{2}b}\left(-2b{\text{e}}^{2\frac{r_0}{b}}+{\text{e}}^{2\frac{r_0}{b}}{r}_0+20b{\text{e}}^{\frac{r_0}{b}}-2b-r_0\right){\text{e}}^{\frac{r_0}{b}}{\left(1+{\text{e}}^{\frac{r_0}{b}}\right)}^{-4}\mathrm{.}\end{array}$ (53)

3.9. Medium with an NFW Profile

We assume that the medium around the SN scales with the Navarro-Frenk-White (NFW) distribution as follows:

$\rho \left(r;r_0,b\right)=\{\begin{array}{ll}{\rho }_c\hfill & \text{if}r\le r_0\hfill \\ \frac{{\rho }_c{r}_0{\left(b+r_0\right)}^2}{r{\left(b+r\right)}^2}\hfill & \text{if}r>r_0\hfill \end{array}$ (54)

where ${\rho }_c$ is the density at $r=0$, and $r_0$ is the radius after which the density starts to decrease, see [19]. The total mass swept, $M\left(r\mathrm{<mo>\; ;\; </mo>}{r}_0\mathrm{,}b\mathrm{,}{\rho }_c\right)$, in the interval [0, r] is

$\begin{array}{l}M\left(r\mathrm{<mo>\; ;\; </mo>}{r}_0\mathrm{,}{\rho }_c\mathrm{,}b\right)\\ =\frac{4}{3}{\rho }_c\pi r_0^3+4{\rho }_c{r}_0\pi ln\left(b+r\right)b^2+8{\rho }_c{r}_0^2\pi ln\left(b+r\right)b\\ +4{\rho }_c{r}_0^3\pi ln\left(b+r\right)+4\frac{{\rho }_c{r}_0\pi b^3}{b+r}+8\frac{{\rho }_c{r}_0^2\pi b^2}{b+r}+4\frac{{\rho }_c\pi r_0^{3}b}{b+r}\\ -4{\rho }_c{r}_0\pi ln\left(b+r_0\right)b^2-8{\rho }_c{r}_0^2\pi ln\left(b+r_0\right)b\\ -4{\rho }_c{r}_0^3\pi ln\left(b+r_0\right)-4\frac{{\rho }_c{r}_0\pi b^3}{b+r_0}-8\frac{{\rho }_c{r}_0{}^2\pi b^2}{b+r_0}-4\frac{{\rho }_c\pi r_0^{3}b}{b+r_0}\mathrm{.}\end{array}$ (55)

The differential equation when the energy is conserved for an NFW profile is

$\frac{ODENN}{3b+3r\left(t\right)}=\frac{2}{3}{\rho }_c\pi r_0^3{v}_0^2$ (56)

where

$\begin{array}{l}ODENN\\ =-2r_0{\rho }_c(3ln\left(b+r_0\right)r\left(t\right)b^2+6ln\left(b+r_0\right)r\left(t\right)b{r}_0+3ln\left(b+r_0\right)r\left(t\right)r_0^2\\ +3b^{3}ln\left(b+r_0\right)+6b^2{r}_{0}ln\left(b+r_0\right)+3b{r}_0^{2}ln\left(b+r_0\right)-3ln\left(b+r\left(t\right)\right)r\left(t\right)b^2\\ -6ln\left(b+r\left(t\right)\right)r\left(t\right)b{r}_0-3ln\left(b+r\left(t\right)\right)r\left(t\right)r_0^2-3b^{3}ln\left(b+r\left(t\right)\right)\\ -6ln\left(b+r\left(t\right)\right)b^2{r}_0-3ln\left(b+r\left(t\right)\right)b{r}_0^2+3r\left(t\right)b^2+3r\left(t\right)b{r}_0\\ -r\left(t\right)r_0^2-3r_0{b}^2-4r_0^{2}b)\pi {\left(\frac{\text{d}}{\text{d}t}r\left(t\right)\right)}^2\mathrm{.}\end{array}$ (57)

The velocity as a function of the radius is

$v\left(r\mathrm{<mo>\; ;\; </mo>}{r}_0\mathrm{,}b\right)=\frac{\sqrt{b+r}{v}_0{r}_0}{VELDD}$ (58)

where

$\begin{array}{l}VELDD\\ =(3b^{3}ln\left(b+r\right)+6b^2{r}_{0}ln\left(b+r\right)+3b^{2}rln\left(b+r\right)+3b{r}_0^{2}ln\left(b+r\right)\\ +6b{r}_{0}rln\left(b+r\right)+3r_0^{2}rln\left(b+r\right)-3b^{3}ln\left(b+r_0\right)-6b^2{r}_{0}ln\left(b+r_0\right)\\ -3b^{2}rln\left(b+r_0\right)-3b{r}_0^{2}ln\left(b+r_0\right)-6b{r}_{0}rln\left(b+r_0\right)\\ -{3r_0^{2}rln\left(b+r_0\right)+3r_0{b}^2-3b^{2}r+4r_0^{2}b-3b{r}_{0}r+r_0^{2}r)}^{1/2}\mathrm{.}\end{array}$ (59)

This differential equation does not have an analytical solution, so we present the approximation arising from the fourth order Taylor series:

$\begin{array}{l}r\left(t\mathrm{<mo>\; ;\; </mo>}{r}_0\mathrm{,}{v}_0\mathrm{,}{t}_0\mathrm{,}b\right)\\ \approx r_0+v_0\left(t-t_0\right)-\frac{3}{4}\frac{v_0^2{\left(t-t_0\right)}^2}{r_0}+\frac{1}{4}\frac{v_0^3\left(5b+7r_0\right){\left(t-t_0\right)}^3}{r_0^2\left(b+r_0\right)}\mathrm{.}\end{array}$ (60)

4. Astrophysical Applications

We now test the reliability of the numerical and approximate solutions on four SNRs: Tycho, see [20], Cas A, see [21], Cygnus loop, see [22], and SN 1006, see [23]. The three astronomically measurable parameters are the time since the explosion in years, t, the actual observed radius in pc, r, and the present velocity of expansion in km∙s⁻¹, see Table 1. The astrophysical units are pc for length and yr for time. With these units, the initial velocity is $v_0\left(\text{km}\cdot {\text{s}}^{-1}\right)=9.7968\times {10}^5{v}_0\left(\text{pc}\cdot {\text{yr}}^{-1}\right)$. In all the models here considered, the initial velocity, $v_0$, is constant in the time interval $\left[0,t_0\right]$.

The goodness of the model is evaluated through the percentage error ${\delta }_r$ of the radius, which is

${\delta }_r=\frac{\left|r_{theo}-r_{obs}\right|}{r_{obs}}\times \mathrm{100,}$ (61)

where $r_{obs}$ is the radius of the SNR as given by the astronomical observations and $r_{theo}$ is the radius suggested by the model. In an analogous way, we can define the percentage error of the velocity. Another useful astrophysical variable is the predicted decrease in the theoretical velocity in 10 years, ${\Delta }_{10}v\left(\text{km}\cdot {\text{s}}^{-1}\right)$.

4.1. Constant Density

The numerical results for the medium with constant density are presented in Table 2.

4.2. Power Law Densities

The results for a medium with an hyperbolic density are presented in Table 3, those for the medium with an inverse square profile of density are presented in Table 4, and those for the medium with an inverse power law profile of density are presented in Table 5.

Table 1. Observed astronomical parameters of the SNRs.

Table 2. Theoretical parameters of the SNRs for the equation of motion in the case of conservation of energy with constant density, see Section 3.1.

Table 3. Theoretical parameters of the SNRs for the equation of motion in the case of conservation of energy with an hyperbolic profile of density, see Section 3.3.

Table 4. Theoretical parameters of the SNRs for the equation of motion in the case of conservation of energy with an inverse square profile of density, see Section 3.4.

Table 5. Theoretical parameters of the SNRs for the equation of motion in the case of conservation of energy with a power law profile of density when $\alpha =1.5$, see Section 3.5.

In the case of a density which decreases with a power law profile we have already pointed out the absence of an analytical solution. As a consequence, Figure 1 presents the asymptotic approximate trajectory as given by (34) for Tycho in the full range of time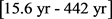. Figure 2 presents the Taylor approximation of the trajectory as given by (32) in the restricted range of time.

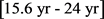Figure 1. Numerical solution (full red line) and asymptotic approximate solution (blue dashed line) for the inverse power law with 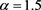Parameters as in Table 5 for Tycho.

Figure 2. Numerical solution (full red line) and Taylor approximation (blue dashed line) for the inverse power law with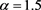. Parameters as in Table 5 for Tycho.

4.3. Presence of an Exponential

The astrophysical parameters for an exponential profile of density are presented in Table 6 and the fit of the trajectory with a Taylor expansion, see Equation (40), is presented in Figure 3.

The astrophysical parameters for a Gaussian profile of density are presented in Table 7 and the fit of the trajectory with a Taylor expansion, see Equation (45), is presented in Figure 4.

4.4. Autogravitating Medium

The astrophysical parameters for an autogravitating medium are presented in Table 8 and the fit of the trajectory with a Taylor expansion, see Equation (53), is presented in Figure 5.

4.5. NFW Profile

The astrophysical parameters for an NFW profile of density are presented in Table 9 and the fit of the trajectory with a Taylor expansion, see Equation (60), is presented in Figure 6.

Table 6. Theoretical parameters of the SNRs for the equation of motion in the case of conservation of energy with an exponential profile of density, see Section 3.6.

Table 7. Theoretical parameters of the SNRs for the equation of motion in the case of conservation of energy with a Gaussian profile of density, see Section 3.7.

Table 8. Theoretical parameters of the SNRs for the equation of motion in the case of conservation of energy with an autogravitating profile of density, see Section 3.8.

Table 9. Theoretical parameters of the SNRs for the equation of motion in the case of conservation of energy with an NFW profile of density, see Section 3.9.

Figure 3. Numerical solution (full red line) and Taylor approximation (blue dashed line) for the exponential profile. Parameters as in Table 6 for Tycho.

Figure 4. Numerical solution (full red line) and Taylor approximation (blue dashed line) for the Gaussian profile. Parameters as in Table 7 for Tycho.

Figure 5. Numerical solution (full red line) and Taylor approximation (blue dashed line) for the autogravitating profile. Parameters as in Table 8 for Tycho.

Figure 6. Numerical solution (full red line) and Taylor approximation (blue dashed line) for an NFW profile. Parameters as in Table 9 for Tycho.

5. Conclusion

The thin layer approximation in the framework of the conservation of energy is an alternative to the use of the conservation of momentum in order to find the equation of motion for a supernova remnant (SNR). In the case where the interstellar medium (ISM) has a constant density, it is possible to find the trajectory in an analytical form, see Equation (11). The case of energy conservation in a medium with variable density was also explored but an analytical trajectory was found only

Table 10. Synoptical parameters of the best model for SNRs with different density profiles.

in the case of a medium characterized by an inverse square decrease of density, see Equation (26). The other profiles of density require a numerical integration in order to find the trajectory. A Taylor series can provide the trajectory for a short interval of time: see Figure 2 for a power law, Figure 3 for an exponential law, Figure 4 for a Gaussian law, Figure 5 for an autogravitating medium and Figure 6 for a Navarro-Frenk-White (NFW) density profile. As an astrophysical target we have chosen to reproduce 4 standard SNRs. The match between the observed and simulated radius as well as that between the observed velocity and the simulated velocity has been analysed in terms of the percentage error, see Tables 2-9. Table 10 presents in column 2 the best model for the SNRs here analysed. The solution for the velocity to first order allows the insertion of the back reaction, i.e. the radiative losses, in the equation for the energy conservation, see Equation (18), and as a consequence the velocity corrected to second order, see Equation (19). The radiative losses allow evaluating the length at which the advancing velocity of the SNR is zero.

Conflicts of Interest

The author declares no conflicts of interest regarding the publication of this paper.

References

[1]	Bisnovatyj-Kogan, G.S. and Blinnikov, S.I. (1982) Sphericization of the Remnants of an Asymmetric Supernova Outburst in a Homogeneous Medium. Astronomicheskii Zhurnal, 59, 876.
[2]	Tenorio-Tagle, G. and Palous, J. (1987) Giant-Scale Supernova Remnants: The Role of Differential Galactic Rotation and the Formation of Molecular Clouds. Astronomy & Astrophysics, 186, 287.
[3]	MacLow, M.M. and McCray, R. (1988) Superbubbles in Disk Galaxies. The Astrophysical Journal, 324, 776-785. https://doi.org/10.1086/165936
[4]	McCray, R.A. (1987) Coronal Interstellar Gas and Supernova Remnants. In: Dalgarno, A. and Layzer, D., Eds., Spectroscopy of Astrophysical Plasmas, Cambridge University Press, Cambridge, UK, 255-278. https://doi.org/10.1017/CBO9780511564659.011
[5]	Kompaneyets, A.S. (1960) A Point Explosion in an Inhomogeneous Atmosphere. Soviet Physics-Doklady, 5, 46.
[6]	Bisnovatyi-Kogan, G.S., Blinnikov, S.I. and Silich, S.A. (1989) Supernova Remnants and Expanding Supershells in Inhomogeneous Moving Medium. Astrophysics and Space Science, 154, 229. https://doi.org/10.1007/BF00642807
[7]	Dyson, J.E. and Williams, D.A. (1997) The Physics of the Interstellar Medium. Institute of Physics Publishing, Bristol. https://doi.org/10.1887/075030460X
[8]	Bisnovatyi-Kogan, G.S. and Silich, S.A. (1998) IAU Colloq. 166: The Local Bubble and Beyond. Volume 506, Springer, Berlin, 137-140. https://doi.org/10.1017/S025292110007086X
[9]	Padmanabhan, P. (2001) Theoretical Astrophysics. Vol. II: Stars and Stellar Systems. Cambridge University Press, Cambridge, UK.
[10]	Chen, Y., Zhang, F., Williams, R.M. and Wang, Q.D. (2003) Supernova Remnant Crossing a Density Jump: A Thin-Shell Model. The Astrophysical Journal, 595, 227. https://doi.org/10.1086/377353
[11]	De Young, D.S. (2002) The Physics of Extragalactic Radio Sources. University of Chicago Press, Chicago, IL.
[12]	Zaninetti, L. (2015) Classical and Relativistic Conservation of Momentum Flux in Radio-Galaxies. Applied Physics Research, 7, 43. https://doi.org/10.5539/apr.v7n4p43
[13]	Zaninetti, L. (2016) Classical and Relativistic Flux of Energy Conservation in Astrophysical Jets. Journal of High Energy Physics, Gravitation and Cosmology, 1, 41. https://doi.org/10.4236/jhepgc.2016.21005
[14]	Olver, F.W.J., Lozier, D.W., Boisvert, R.F. and Clark, C.W. (2010) NIST Handbook of Mathematical Functions. Cambridge University Press, Cambridge.
[15]	Spitzer Jr., L. (1942) The Dynamics of the Interstellar Medium. III. Galactic Distribution. The Astrophysical Journal, 95, 329. https://doi.org/10.1086/144407
[16]	Rohlfs, K. (1977) Lectures on Density Wave Theory. In: Lecture Notes in Physics, Volume 69, Springer-Verlag, Berlin.
[17]	Bertin, G. (2000) Dynamics of Galaxies. Cambridge University Press, Cambridge.
[18]	Padmanabhan, P. (2002) Theoretical Astrophysics. Vol. III: Galaxies and Cosmology. Cambridge University Press, Cambridge, UK.
[19]	Navarro, J.F., Frenk, C.S. and White, S.D.M. (1996) The Structure of Cold Dark Matter Halos. The Astrophysical Journal, 462, 563. https://doi.org/10.1086/177173
[20]	Williams, B.J., Chomiuk, L., Hewitt, J.W., Blondin, J.M., Borkowski, K.J., Ghavamian, P., Petre, R. and Reynolds, S.P. (2016) An X-Ray and Radio Study of the Varying Expansion Velocities in Tycho Supernova Remnant. The Astrophysical Journal Letters, 823, L32. https://doi.org/10.3847/2041-8205/823/2/L32
[21]	Patnaude, D. and Fesen, R.A. (2009) Proper Motions and Brightness Variations of Nonthermal X-Ray Filaments in the Cassiopeia A Supernova Remnant. The Astrophysical Journal, 697, 535. https://doi.org/10.1088/0004-637X/697/1/535
[22]	Chiad, B.T., Ali, L.T. and Hassani, A.S. (2015) Determination of Velocity and Radius of Supernova Remnant after 1000 yrs of Explosion. International Journal of Astronomy and Astrophysics, 5, 125. https://doi.org/10.4236/ijaa.2015.52016
[23]	Uchida, H., Yamaguchi, H. and Koyama, K. (2013) Asymmetric Ejecta Distribution in SN 1006. The Astrophysical Journal, 771, 56. https://doi.org/10.1088/0004-637X/771/1/56