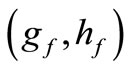Probabilistic Simulation Approach to Evaluate the Tooth-Root Strength of Spur Gears with FEM-Based Verification ()
1. Introduction
Traditional deterministic design approaches compensate for uncertainties through the use of empirical safety factors, which do not provide sufficient information to achieve optimal use of available resources in terms of material, manufacturing and operational costs [1]. For example, components resulting from such conventional design methods are either over-safe leading to wastage of resources or unsafe leading to unexpected failures. They fail to provide the necessary understanding of the variability associated with the properties of materials, manufacturing tolerances and in-service loading. To design a product that will perform a function reliably, the reliability must be considered as an important functional requirement all the way through the design process, from the customer’s need to the final product [2]. Addressing these issues comprehensively at an early design stage is necessary to produce competitive product that functions consistently during its intended service life [3]. Indeed, consistent levels of safety and reliability can be achieved based on the probabilistic design methods.
Probabilistic design, such as reliability-based design and robust design, offers tools for making reliable decisions with the consideration of uncertainty associated with design variables/parameters and simulation models [4,5]. It allows the designer to assess the reliability of the mechanical system. This is impossible with the factor of safety approach. One important task of a probabilistic design is uncertainty analysis, through which we understand how much the impact of the uncertainty associated with the system input is on the system output by identifying the probabilistic characteristics of system output. The uncertainty in a design performance is described probabilistically (e.g., Normal Distribution) by its mean (μ), variance (σ2), the probability density function (PDF), or the cumulative distribution function (CDF), etc. By understanding the probability distributions of the design parameters, the designer can design for a specific reliability or quality level by producing designs that are robust to variations. Figure 1 shows the difference between deterministic method and the SSI method as a probabilistic design tool for estimating reliability. The area representing the unreliability is a part of the area of the interference. The unreliability of the mechanical component is determined by the probability that the failure governing stress exceeds the failure governing strength. Once the failure governing stress and strength distributions are available, the unreliability or reliability of the component can be obtained by using the stress-strength distribution interference approach.
The life and reliability of mechanical systems such as the gearboxes depend on the life/reliability characteristics of their components at a certain defined load [6]. Gears, as the most important gearbox components, are relatively complex machine elements and there are many design parameters involved in their design. Their design methodology involves selecting appropriate attributes from a large amount of engineering/standards data available in catalogues and design handbooks [7]. Gears are generally designed based on endurance (fatigue characteristics) design standards. They should be selected and shaped to either endure a “nominal” i.e. rated load condition or unlimited load cycles. Stresses such as the bending stress at the tooth root under the nominal load must be below the endurance limit. The endurance limit values themselves are not “exact”, but “statistical”. For this reason, design standards such as AGMA, ISO, DIN, etc. include a number of factors such as size, surface, life, load, velocity, etc. to adjust the endurance limit “to be on the safe side”. However, the gear tooth strengths are obtained using deterministic models without sufficient knowledge of their statistical distribution. Furthermore, the variation in the gear tooth strength may also be affected by a combination of variations in the metallurgical and fabrication processes involved with its manufacture, dimensional inaccuracy, surface damage, etc., whereas fluctuations in the load imposed upon it may originate from variations in its duty and environment. Therefore, design of gears for specified design reliability may benefit from detailed distribution data of gear tooth strength.
There are two failure modes that are important causes of gear tooth failures. Bending stress (leading to tooth breakage) which is a maximum at the tooth root, and compressive stress (leading to pitting), which reaches a maximum value at the tooth face. Because the tooth loading is cyclic, both of these stress mechanisms impose a fatigue loading condition on this machine component element. Tooth breakage due to the stress concentration and crack initiation at the non-involute portion of gear tooth, when stresses significantly exceeds the maximum allowable stress in gear transmission units can be extremely dangerous in automotive, aerospace, or space industry applications. The non-involute portion of the tooth profile, the fillet, has a direct effect on the motion/force transmission. The detailed geometry of the fillet influences the maximum bending stresses developed at the root of the gear tooth and is determined by the gear cutting manufacturing process and cutting tool dimensions [8]. Hence, it is necessary to have a detailed knowledge of the root fillet geometry and its effect on the tooth bending stresses.
In the following sections, a special attention is given to the analysis of the impact of the gear tooth fillet portion on the maximum bending stress value and its distribution along the fillet portion. The SSI theory as a probabilistic design tool will be used to examine the influence of root fillet contour on the gear tooth strength for four gear sets with different fillet profiles.
2. Investigate the Effect of the Root Fillet Portion on the Gear Tooth Strength
According to the theory of gearing, the procedure for generating the exact geometry of the tooth profile must be modelled to follow the actual generation process which is used in production of real gears [9-11]. The generation of spur gear tooth shape during hobbing process is modelled to be equivalent to pure rolling of the pitch line of rack against the pitch circle of gear blank. The fillet curve of the gear belongs to the trochoid family and it is conjugate to the tip of the generating rack, as shown in Figure 2. The radius of curvature of the trochoid fillet varies along the fillet curve. In the following section, the mathematical model of the trochoid fillet is developed to investigate the effect of the trochoid fillet conditions on the root strength of the gear tooth.
Figure 2 shows an arbitrary position during a cycle of contact in a transverse plane between the generating hob tool and the gear tooth. According to AGMA 930-A05, the center of the rounded corner at the tip of the rack is located on the basic rack by its coordinates