There Are Infinitely Many Mersnne Composite Numbers with Prime Exponents

Fengsui Liu

Department of Mathematics, Nanchang University, Nanchang, China.

DOI: 10.4236/apm.2018.87041                

Abstract

By extending both arithmetical operations into finite sets of natural numbers, from the entire set of natural numbers successively deleting some residue classes modulo a prime, we invented a recursive sieve method or algorithm on natural numbers and their sets. The algorithm mechanically yields a sequence of sets, which converges to the set of all primes p such that 2p + 1 divides the Mersenne number M_p. The cardinal sequence corresponding to the sequence of sets is strictly increasing. So that we have captured enough usable structures, without any estimation, the existing theories of those structures allow us to prove an exact result: there are infinitely many Mersenne composite numbers with prime exponents M_p.

Keywords

Mersenne Composite Numbers, Sophie German Primes, Recursive Algorithm, Order Topology, Limit of Sequence of Sets

1. Introduction

A Mersenne number $M_x$ is a number of the form

$M_x=2^x-1.$

They are named after Marin Mersenne, a French Minim friar, who studied them in the early 17th century.

If the exponent x is a composite number, obviously $M_x$ is a composite number. One only discusses the primality of a Mersenne number with a prime exponent.

On January 3, 2018, the Great Internet Mersenne Prime Search has discovered the largest known prime number, 2^77232917−1, having 23,249,425 digits. A computer volunteered by Jonathan Pace made the find on December 26, 2017 [1] .

One has a conjecture and an open problem about Mersenne numbers.

There are infinitely many Mersenne primes.

There are infinitely many Mersenne composite numbers.

In 1750 Euler stated and in 1775 Laglange proved the following theorem [2] .

Let $p\equiv 3\mathrm{mod}4$ is prime. Then $2p+1$ is also primeif and only if $2p+1$ divides M_p.

When p and $2p+1$ both are prime, the prime p is said to be a Sophie Germain prime.

If we prove that there are infinitely many Sophie Germain primes of the form $4k+3$ , then we prove that there are infinitely many Mersenne composite numbers.

In normal sieve theory, like the twin prime conjecture, it is hopeless to prove the Sophie German prime conjecture.

Primes have some obvious structures. We don’t know if they also have some additional structures. Because ofthis, we have been unable to settle many questions about primes [3] .

In 2014, Simon Davis provided a probabilistic proof of infinite extent of the sequence of Mersenne composite numbers with prime exponents [4] .

In 2011, author used the recursive sieve method, which reveals some exotic structures for sets of primes, to prove the Sophie Germain prime conjecture: there are infinitely many primes p such that $2p+1$ is also prime [5] .

In this paper we extend the above structural result to prove: there are infinitely many Sophie Germain primes of the form $4k+3$ , then we solve the open problem about Mersenne composite numbers.

In order to be self-contained, we repeat some contents in the paper [5] .

2. A Formal System

For expressing a recursive sieve method by well formed formulas, we extend both arithmetical operations addition +, multiplication × on natural numbers into finite sets of natural numbers.

We use small letters $a,x,t$ to denote natural numbers and capital letters $A,X,T$ to denote sets of natural numbers.

For arbitrary both finite sets of natural numbers $A,B$ we write

$A=\langle a_1,a_2,\cdots ,a_i,\cdots ,a_n\rangle ,a_1<a_2<\cdots <a_i<\cdots <a_n$ ,

$B=\langle b_1,b_2,\cdots ,b_j,\cdots ,b_m\rangle ,b_1<b_2<\cdots <b_j<\cdots <b_m$ .

We define

, (2.1)

$AB=\langle a_1{b}_1,a_2{b}_1,\cdots ,a_i{b}_j,\cdots ,a_{n-1}{b}_m,a_n{b}_m\rangle .$

Example:

$\langle 1,5\rangle +\langle 0,6,12,18,24\rangle =\langle 1,5,7,11,13,17,19,23,25,29\rangle ,$

$\langle 6\rangle \langle 0,1,2,3,4\rangle =\langle 0,6,12,18,24\rangle .$

For the empty set $\varphi$ we define $\varphi +A=\varphi$ and $\varphi A=\varphi$ .

We write $A\backslash B$ for the set difference of A and B.

Let

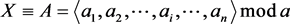
be several residue classes modulo a.

We define the solution of the system of congruences

$X\equiv A=\langle a_1,a_2,\cdots ,a_i,\cdots ,a_n\rangle \mathrm{mod}a$ ,

$X\equiv B=\langle b_1,b_2,\cdots ,b_j,\cdots ,b_m\rangle \mathrm{mod}b$

to be

$X\equiv D=\langle d_{11},d_{21},\cdots ,d_{ij},\cdots ,d_{nm}\rangle \mathrm{mod}ab$ (2.2)

where $x=d_{ij}\mathrm{mod}ab$ is the solution of the system of congruences

$x=a_i\mathrm{mod}a,$

$x=b_j\mathrm{mod}b.$

If the greatest common divisor $\left(a,b\right)$ equals 1, by the Chinese remainder theorem, every solution $x=d_{ij}\mathrm{mod}ab$ exists with $d_{ij}<ab$ , every solution is computable and unique.

Except extending +, × into finite sets of natural numbers, we continue the traditional interpretation of the formal language 0, 1, +, ×, $\in$ . The reader who is familiar with model theory may know, we have founded a new model or structure of second order arithmetic by a two-sorted logic

$\langle P\left(N\right),N,0,1,+,\times ,\in \rangle ,$ (2.3)

where N is the set of all natural numbers and $P\left(N\right)$ is the power set of N.

We denote this model by $P\left(N\right)$ .

Given a interpretation of the formal language 0, 1, +, ×, $\in$ , the set of true sentences in $P\left(N\right)$ , the theory of the model, is entirely determined. The entities in $P\left(N\right)$ have intrinsic objective nature. Example the set of all primes p such that $2p+1|M_p$ have intrinsic objective nature, infinite or not.

Mathematicians assume that $\langle N,0,1,+,\times \rangle$ is the standard model of Peano theory PA,

$N\models PA$ (2.4)

Similarly, we assume that $\langle P\left(N\right),N,0,1,+,\times ,\in \rangle$ is the standard model of a new arithmetical theory $PA+ZF$ ,

$P\left(N\right)\models PA+ZF$ . (2.5)

This is a joint theory of PA and ZF, in other words, $P\left(N\right)$ is not only a model of Peano theory PA but also is a model of set theory ZF.

As a model of Peano theory PA the natural numbers in the model $P\left(N\right)$ and the natural numbers in the model N are the same.

As a model of set theory ZF the natural numbers are atoms, urelements, or objects that have no element. We discuss sets of natural numbers and sets of sets of natural numbers.

The model $P\left(N\right)$ and the theory $PA+ZF$ construct a new formal system. In this formal system $P\left(N\right)$ , we may formalize natural numbers and sets of natural numbers as individuals, terms, or points.

We do not know if the theory $PA+ZF$ can solve the open problem, but we know that the new formal language 0, 1, +, ×, $\in$ has more stronger expressive power. The new formal system $P\left(N\right)$ has more richer mathematical structures.

In the formal system $P\left(N\right)$ , we may introduce a recursive algorithm and produce some recursive sequences of sets. A new notation, the sequence of sets, reveals structures for some prime sets. Based on the theory $PA+ZF$ and the existing theories of those structures, we can carefully construct a logical deduction, which is built into the structures of the natural numbers and their sets, to solve some old prime problems in pure mathematics.

“A well chosen notation can contribute to making mathematical reasoning itself easier, or even purely mechanical.” [6] .

We do not further discuss this formal system in view from logic and mathematical foundation

3. A Recursive Algorithm or Sieve Method

From the entire set of natural numbers successively deleting some residue classes modulo a prime, we invented a recursive sieve method or algorithm on natural numbers and their sets. Now we introduce the algorithm for Sophie Germain primes of the form $4k+3$ .

Let $p_i$ be i-th prime, $p_0=2$ . For every prime $p_i>2$ , let

$B_i\equiv \langle 0,\left(p_i-1\right)/2\rangle \mathrm{mod}{p}_i$ (3.1)

be the solution of the congruence

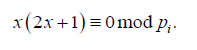
Example:

$B_1\equiv \langle 0,1\rangle \mathrm{mod}3,$

$B_{\text{2}}\equiv \langle 0,\text{2}\rangle \mathrm{mod}\text{5},$

$B_{\text{3}}\equiv \langle 0,\text{3}\rangle \mathrm{mod}\text{7},$

$B_{\text{4}}\equiv \langle 0,\text{5}\rangle \mathrm{mod}\text{11},$

Let

$m_{i+1}=\text{4}{\displaystyle {\prod }_{\text{1}}^i{p}_j}.$ (3.2)

From the residue class $x\equiv 3\mathrm{mod}4$ we successively delete the residue classes $B_1\mathrm{mod}3$ , $\cdots$ , $B_i\mathrm{mod}{p}_i$ leave the residue class $T_{i+1}\mathrm{mod}{m}_{i+1}$ . Then the left residue class is the set of all numbers x of the form $4k+3$ such that $x\left(2x+1\right)$ does not contain any prime $p_j<p_i$ as a factor $\left(x\left(2x+1\right),m_{i+1}\right)=1$ .

Let

$X\equiv D_i\mathrm{mod}{m}_{i+1}$ (3.3)

be the solution of the system of congruences

$X\equiv T_i\mathrm{mod}{m}_i$

$X\equiv B_i\mathrm{mod}{p}_i$

Let $T_{i+1}$ be the set of least nonnegative representatives of the left residue class $T_{i+1}\mathrm{mod}{m}_{i+1}$ .

In the formal system $P\left(N\right)$ we obtain a recursive formula for the set $T_{i+1}$ , which describe the recursive algorithm or sieve method for Sophie Germain primes of the form $4k+3$ .

$T_1=\langle 3\rangle ,$

$T_{i+1}=\left(T_i+\langle m_i\rangle \langle 0,1,2,\cdots ,p_i-1\rangle \right)\backslash D_i.$ (3.4)

The number of elements of the set $T_{i+1}$ is

$\left|T_{i+1}\right|={\displaystyle {\prod }_1^i\left(P_i-2\right)}.$ (3.5)

We exhibit the first few terms of formula (3.4) and briefly prove that the algorithm is valid by mathematical induction.

The residue class $T_1=\langle 3\rangle \mathrm{mod}4$ is the set of all numbers x of the form $4k+3$ . Now the set $X\equiv \langle 3\rangle \mathrm{mod}4$ is equivalent to the set

$X\equiv \left(\langle 3\rangle +\langle 4\rangle \langle 0,1,2\rangle \right)\mathrm{mod}12$ ,

from them we delete the solution of the system of congruences $D_1=\langle 3,7\rangle \mathrm{mod}\text{12}$ , and leave

$T_2=\left(\langle 3\rangle +\langle 4\rangle \langle 0,1,2\rangle \right)\backslash \langle 3,7\rangle =\langle 11\rangle .$

The residue class $T_{\text{2}}=\langle \text{11}\rangle \mathrm{mod}\text{12}$ is the set of all numbers x of the form $4k+3$ such that $\left(x\left(2x+1\right),12\right)=1$ . Now the set $X\equiv \langle \text{11}\rangle \mathrm{mod}\text{12}$ is equivalent to the set

$X\equiv \left(\langle 11\rangle +\langle 12\rangle \langle 0,1,2,3,4\rangle \right)\mathrm{mod}60$

from them we delete the solution of the system of congruences

$D_2=\langle 35,47\rangle \mathrm{mod}60,$

and leave

$T_3=\left(\langle 11\rangle +\langle 12\rangle \langle 0,1,2,3,4\rangle \right)\backslash \langle 35,47\rangle =\langle 11,23,59\rangle .$

The residue class $T_3=\langle 11,23,59\rangle \mathrm{mod}60$ is the set of all numbers x of the form $4k+3$ such that $\left(x\left(2x+1\right),60\right)=1$ . And so on.

Suppose that the residue class $T_i\mathrm{mod}{m}_i$ is the set of all numbers x of the form $4k+3$ such that $\left(x\left(2x+1\right),m_i\right)=1$ . We delete the residue class $B_i\mathrm{mod}{p}_i$ from them. In other words, we delete the solution $X\equiv D_i\mathrm{mod}{m}_{i+1}$ of the system of congruences

$X\equiv T_i\mathrm{mod}{m}_i$

$X\equiv B_i\mathrm{mod}{p}_i$

Now the residue class $T_i\mathrm{mod}{m}_i$ is equivalent to the residue class

$\left(T_i+\langle m_i\rangle \langle 0,1,2,\cdots ,p_i-1\rangle \right)\mathrm{mod}{m}_{i+1}$

From them we delete the solution $D_i\mathrm{mod}{m}_{i+1}$ , which is the set of all numbers x of the form $4k+3$ such that $x\left(2x+1\right)\equiv 0\mathrm{mod}{p}_i$ . It follows that the left residue class $T_{i+1}\mathrm{mod}{m}_{i+1}$ is the set of all numbers x of the form $4k+3$ , and $\left(x\left(2x+1\right),m_{i+1}\right)=1$ . Our algorithm is valid. It is easy to compute

$\left|T_{i+1}\right|=\left|T_i\right|\left(p_i-2\right)$

by the above algorithm.

We may rigorously prove formulas (3.4) and (3.5) by mathematical induction, the proof is left to the reader.

In the next section we refine formula (3.4) and solve the open problem

4. A Main Theorem

We call a Sophie Germain primes of the form $4k+3$ a S-prime.

Let $T_e$ be the set of all S-primes

$T_e=\left\{x:x\text{isaS-prime}\right\}$ . (4.1)

By the recursive sieve method we shall determine an additional exotic structure for the set $T_e$ based on the limit of a sequence of sets ( ${T^{\prime }}_i$ ),

$\lim {T^{\prime }}_i=T_e.$

Next we prove that the cardinality of the set $T_e$ is infinite by existing theories of those structures,

$\left|T_e\right|={\aleph }_0.$

Based on the recursive algorithm, formula (3.4), we successively delete all numbers x of the form $4k+3$ such that $x\left(2x+1\right)$ contains the least prime factor $p_i$ . We delete non S-primes or non S-primes together with a S-prime. The sifting condition or “sieve” is

$x\left(2x+1\right)\equiv 0\mathrm{mod}{p}_i.$ (4.2)

We modify the sifting condition to be

$x\left(2x+1\right)\equiv 0\mathrm{mod}{p}_i\wedge p_i<x.$ (4.3)

According to this new sifting condition or “sieve”, we successively delete the set $C_i$ of all numbers x such that either x or $2x+1$ is composite with the least prime factor $p_i>2$ ,

$C_i=\left\{x:x\in X\equiv T_i\mathrm{mod}{m}_i\wedge x\left(2x+1\right)\equiv 0\mathrm{mod}{p}_i\wedge p_i<x\right\}.$ (4.4)

but remain the S-prime x if $p_i=x$ .

We delete all sets $C_j$ with $1\le j<i$ from the set $N_0$ of all natural numbers x of the form $4k+3$ , and leave the set

$L_i=N_0\backslash {\displaystyle {\cup }_1^{i-1}{C}_j}.$ (4.5)

The set of all S-primes is

$T_e=N_0\backslash {\displaystyle {\cup }_1^{\infty }{C}_i}.$ (4.6)

The recursive sieve (4.3) is a perfect tool, with this tool we delete all non S-primes and leave all S-primes. So that we only need to determine the number of all S-primes $\left|T_e\right|$ . If we do so successfully, then the parity obstruction, a ghost in house of primes, has been automatically evaporated.

With the recursive sieve (4.3), each non S-prime is deleted exactly once, there is need neither the inclusion-exclusion principle nor the estimation of error terms, which cause all the difficulty in normal sieve theory.

Let $A_i$ be the set of all S-primes x less than $p_i$

$A_i=\left\{x:x<p_i\wedge x\text{isaS-prime}\right\}$ . (4.7)

From the recursive formula (3.4), we deduce that the left set $L_i$ is the union of the set $A_i$ of S-primes and the residue class $T_i\mathrm{mod}{m}_i$ .

$L_i=A_i\cup T_i\mathrm{mod}{m}_i$ (4.8)

Now we intercept the initial segment from the left set $L_i$ , which is the union of the set $A_i$ of S-primes and the set $T_i$ of least nonnegative representatives. Then we obtain a new recursive formula

${T^{\prime }}_i=A_i\cup T_i.$ (4.9)

Except remaining all S-primes x less than $p_i$ in the initial segment ${T^{\prime }}_i$ , both sets ${T^{\prime }}_i$ and $T_i$ are the same.

For example

$\begin{array}{c}{T^{\prime }}_4=\langle 3\rangle \cup \langle 11,23,71,\cdots ,263,299,323,359,383,419\rangle \\ =\langle 3,11,23,71,\cdots ,263,299,323,359,383,419\rangle \end{array}$

Note: the $M_3=2\times 3+1=7$ is a prime. For all S-prime $p>3$ , $2p+1|M_p$ , the $M_p$ is a Mersenne composite number. Example: $M_{11},M_{23},M_{83},\cdots$ .

Formula (4.9) expresses the recursively sifting process according to the sifting condition (4.3), and provides a recursive definition of the initial segment ${T^{\prime }}_i$ . The initial segment is a well chosen notation. We shall consider some properties of the initial segment, and reveal some structures of the sequence of the initial segments to determine the set of all S-primes and its cardinality.

Let $\left|A_i\right|$ be the number of S-primes less than $p_i$ . Then the number of elements of the initial segment ${T^{\prime }}_i$ is

$\left|{T^{\prime }}_i\right|=\left|A_i\right|+\left|T_i\right|.$ (4.10)

From formula (3.5) we deduce that the cardinal sequence $\left|{T^{\prime }}_i\right|$ is strictly increasing

$\left|{T^{\prime }}_i\right|<\left|{T^{\prime }}_{i+1}\right|.$ (4.11)

Based on order topology obviously we have

$\lim \left|{T^{\prime }}_i\right|={\aleph }_0.$ (4.12)

Intuitively we see that the initial segment ${T^{\prime }}_i$ approaches the set of all S-primes $T_e$ , and the corresponding cardinality $\left|{T^{\prime }}_i\right|$ approaches infinity as $i\to \infty$ . Thus the set of all S-primes is limit computable and is an infinite set.

Next we give a formal proof based on set theory and order topology

4.1. A Formal Proof

Let $A_i{}^{\prime }$ be the subset of all S-primes in the initial segment ${T^{\prime }}_i$

$A_i{}^{\prime }=\left\{x\in {T^{\prime }}_i:x\text{isS-prime}\right\}$ . (4.13)

We consider the structures of both sequences of sets $\left(T_i{}^{\prime }\right)$ and $\left(A_i{}^{\prime }\right)$ to solve the open problem.

Lemma 4.1:

The sequence of the initial segments $\left(T_i{}^{\prime }\right)$ and the sequence of its subsets $\left(A_i{}^{\prime }\right)$ of S-primes both converge to the set of all S-primes $T_e$ .

First from set theory, next from order topology we prove this Lemma.

Proof:

For the convenience of the reader, we quote a definition of the set theoretic limit of a sequence of sets [7] .

Let $F_n$ be a sequence of sets, we define $\underset{n\to \infty }{\lim \sup }{F}_n$ and $\underset{n\to \infty }{\lim \inf }{F}_n$ as follows

$\underset{n\to \infty }{\lim \sup }{F}_n={\displaystyle {\cup }_0^{\infty }{\displaystyle {\cap }_0^{\infty }{F}_n}}.$ (4.14)

$\underset{n\to \infty }{\lim \inf }{F}_n={\displaystyle {\cup }_0^{\infty }{\displaystyle {\cap }_0^{\infty }{F}_n}}.$ (4.15)

It is easy to check that $\underset{n\to \infty }{\lim \sup }{F}_n$ is the set of those elements x, which belongs to $F_n$ for infinitely many n. Analogously, x belongs to $\underset{n\to \infty }{\lim \inf }{F}_n$ if and only if it belongs to $F_n$ for almost all n, that is it belongs to all but a finite number of the $F_n$ .

If

$\underset{n\to \infty }{\lim \sup }{F}_n=\underset{n\to \infty }{\lim \inf }{F}_n$ .

we say that the sequence of sets $F_n$ converges to the limit

$\lim F_n=\underset{n\to \infty }{\lim \sup }{F}_n=\underset{n\to \infty }{\lim \inf }{F}_n$ . (4.16)

We know that the sequence of left sets $L_i$ is descending

$L_1\supset L_2\supset \cdots \supset L_i\supset \cdots$ (4.17)

According to the definition of the set theoretic limit of a sequence of sets, we obtain that the sequence of left sets $\left(L_i\right)$ converges to the set $T_e$

$\lim L_i={\displaystyle \cap L_i}=T_e.$ (4.18)

The sequence of subsets $\left(A_i^{.}\right)$ of S-primes is ascending

${A^{\prime }}_1\subset {A^{\prime }}_2\subset \cdots \subset {A^{\prime }}_i\subset \cdots$ (4.19)

We obtain that the sequence of subsets $\left(A_i^{.}\right)$ converges to the set $T_e$ ,

$\lim {A^{\prime }}_i={\displaystyle \cup {A^{\prime }}_i}=T_e.$ (4.20)

The initial segment ${T^{\prime }}_i$ is located between two sets $A_i^{.}$ and $L_i$

${A^{\prime }}_i\subset {T^{\prime }}_i\subset L_i.$ (4.21)

Thus the sequence of the initial segments $\left(T_i^{.}\right)$ converges to the set $T_e$

$\lim {T^{\prime }}_i=T_e.$ (4.22)

According to set theory, we have proved that both sequences of sets $\left(T_i^{.}\right)$ and $\left(A_i^{.}\right)$ converge to the set of all S-primes $T_e$ .

$\lim {A^{\prime }}_i=\lim {T^{\prime }}_i=T_e.$ (4.23)

Next we prove that according to order topology both sequences of sets $\left(T_i^{.}\right)$ and $\left(A_i^{.}\right)$ converge to the set of all S-primes $T_e$ .

We quote a definition of the order topology [8] .

Let X be a set with a linear order relation; assume X has more one element. Let B be the collection of all sets of the following types:

1) All open intervals $\left(a,b\right)$ in X.

2) All intervals of the form $\left[a_0,b\right)$ , where $a_0$ is the smallest element (if any) in X.

3) All intervals of the form $\left(a,b_0\right]$ , where $b_0$ is the largest element (if any) in X.

The collection B is a bases of a topology on X, which is called the order topology.

According to the definition there is no order topology on the empty set or sets with a single element.

The recursively sifting process, formula (4.9), produces both sequences of sets together with the set theoretic limit point $T_e$ .

$X_{\text{1}}:{T^{\prime }}_1,{T^{\prime }}_2,\cdots ,{T^{\prime }}_i,\cdots ,T_e.$

$X_{\text{2}}:{A^{\prime }}_1,{A^{\prime }}_2,\cdots ,{A^{\prime }}_i,\cdots ,T_e.$ (4.24)

We further consider the structures of sets $X_{\text{1}}$ and $X_{\text{2}}$ using the recursively sifting process (4.9) as an order relation

$i<j,{T^{\prime }}_i<{T^{\prime }}_j;{\forall }_i\left({T^{\prime }}_i<T_e\right).$

$i<j,{A^{\prime }}_i<{A^{\prime }}_j;{\forall }_i\left({A^{\prime }}_i<T_e\right).$ (4.25)

The set $X_{\text{1}}$ has no repeated term. It is a well ordered set with the order type $\omega +1$ using the recursively sifting process (4.9) as an order relation. Thus the set $X_{\text{1}}$ may be endowed an order topology.

The set $X_{\text{2}}$ may have some repeated terms. We have computed out the first few S-primes x. The set $X_{\text{2}}$ contains more than one element, may be endowed an order topology using the recursively sifting process (4.9) as an order relation.

Obviously, for every neighborhood $\left(c,T_e\right]$ of $T_e$ there is a natural number $i_0$ , for all $i>i_0$ , we have ${T^{\prime }}_i\in \left(c,T_e\right]$ and ${A^{\prime }}_i\in \left(c,T_e\right]$ , thus both sequences of sets $\left(T_i^{.}\right)$ and $\left(A_i^{.}\right)$ converge to the set of all S-primes $T_e$ .

$\lim {T^{\prime }}_i=T_e,$ (4.26)

$\lim {A^{\prime }}_i=T_e.$ (4.27)

According to the order topology, we have again proved that both sequences of sets $\left(T_i^{.}\right)$ and $\left(A_i^{.}\right)$ converge to the set of all S-primes $T_e$ . We also have

$\lim {T^{\prime }}_i=\lim {A^{\prime }}_i.$ (4.28)

The formula ${T^{\prime }}_i$ is a recursive asymptotic formula for the set of all S-primes $T_e$ .

end proof.

In general, if $T_e=\varphi$ , the set $X_2=\left\{\varphi \right\}$ only has a single element, which has no order topology. In this case formula (4.28) is not valid and our method of proof may be useless [5] .

Lemma 4.1 reveals an order topological structure and a set theoretic structure for the set of all S-primes on the recursive sequences of sets. Based on the existing theories of those structures, we easily prove that the cardinality of the set of all S-primes is infinite.

Theorem 4.2:

The set of all S-primes is an infinite set.

We give two proofs.

Proof A:

We consider the cardinalities $\left|{T^{\prime }}_i\right|$ and $\left|{A^{\prime }}_i\right|$ of sets on two sides of the equality (4.28), and the order topological limits of cardinal sequences $\left(\left|{T^{\prime }}_i\right|\right)$ and $\left(\left|{A^{\prime }}_i\right|\right)$ , as the sets ${T^{\prime }}_i$ and ${A^{\prime }}_i$ both tend to $T_e$ .

From general topology we know, if the limits of both cardinal sequences $\left(\left|{T^{\prime }}_i\right|\right)$ and $\left(\left|{A^{\prime }}_i\right|\right)$ on two sides of the equality (4.28) exist, then both limits are equal; if $\lim \left|{A^{\prime }}_i\right|$ does not exist, then the condition for the existence of the limit $\lim \left|{T^{\prime }}_i\right|$ is not sufficient [8] .

For S-primes, the set $T_e$ is nonempty, the formula (4.28) is valid, obviously the order topological limits $\lim \left|{A^{\prime }}_i\right|$ and $\lim \left|{T^{\prime }}_i\right|$ on two sides of the equality (4.28) exist, thus both limits are equal

$\lim \left|{A^{\prime }}_i\right|=\lim \left|{T^{\prime }}_i\right|.$ (4.29)

From formula (4.12) $\lim \left|{T^{\prime }}_i\right|={\aleph }_0$ we have

$\lim \left|{A^{\prime }}_i\right|={\aleph }_{\text{0}}\text{.}$ (4.30)

Usually let ${\pi }_{\text{2}}\left(n\right)$ be the counting function, the number of S-primes less than or equal to n. Normal sieve theory is unable to provide non-trivial lower bounds of ${\pi }_{\text{2}}\left(n\right)$ because the parity obstruction. Let n be a natural number. Then the number sequence $\left(m_i\right)$ is a subsequence of the number sequence (n), we have

$\lim {\pi }_2\left(n\right)=\lim {\pi }_2\left(m_i\right).$ (4.31)

By formula (4.13), the ${A^{\prime }}_i$ is the set of all S-primes less than $m_i$ , and the $\left|{A^{\prime }}_i\right|$ is the number of all S-primes less than $m_i$ , thus ${\pi }_{\text{2}}\left(m_i\right)=\left|{A^{\prime }}_i\right|$ . We have

$\lim {\pi }_2\left(m_i\right)=\lim \left|{A^{\prime }}_i\right|$ . (4.32)

From formula (4.30) we prove

$\lim {\pi }_2\left(n\right)={\aleph }_{\text{0}}\text{.}$ (4.33)

We directly prove that the number of all S-primes is infinite with the counting function. Next we give another proof by the continuity of the cardinal function.

End proof.

Proof B:

Let $f:X\to Y$ be the cardinal function $f\left(T\right)=\left|T\right|$ . from the order topological space X to the order topological space Y

$X:{T^{\prime }}_1,{T^{\prime }}_2,\cdots ,{T^{\prime }}_i,\cdots ,T_e,$

$Y:\left|{T^{\prime }}_1\right|,\left|{T^{\prime }}_2\right|,\cdots ,\left|{T^{\prime }}_i\right|,\cdots ,{\aleph }_{\text{0}}.$ (4.34)

It is easy to check that for every open set $\left[\left|{T^{\prime }}_1\right|,c\right),\left(c,d\right),\left(d,{\aleph }_0\right]$ in Y the pre-image $\left[{T^{\prime }}_1,c\right),\left(c,d\right),\left(d,T_e\right]$ is also an open set in X. So that the cardinal function $\left|T\right|$ is continuous at $T_e$ with respect to the above order topology.

Both order topological spaces are first countable, hence the cardinal function $\left|T\right|$ is sequentially continuous. By a usual topological theorem [9] (Theorem 21.3, p130), the cardinal function $\left|T\right|$ preserves limits

$\lim \left|{T^{\prime }}_i\right|=\left|\lim {T^{\prime }}_i\right|.$ (4.35)

Order topological spaces are Hausdorff spaces. In Hausdorff spaces the limit

point of the sequence of sets $\left(T_i^{.}\right)$ and the limit point of cardinal sequence

$\left(\left|T_i^{.}\right|\right)$ are unique.

We have proved Lemma 4.1, $\lim {T^{\prime }}_i=T_e$ , and formula (4.12), $\lim \left|{T^{\prime }}_i\right|={\aleph }_0$ . Substitute, we obtain that the set of all S-primes is an infinite set,

$\left|T_e\right|={\aleph }_0.$ (4.36)

End proof.

By Euler-Lagrange theorem we have solved the open problem about Mersenne numbers.

Theorem 4.3:

There are infinitely many Mersenne composite numbers with prime exponents.

4.2. Conclusions

In pure mathematics, without any statistical data, without the Riemann hypothesis, by the recursive algorithm, we well understand the recursive structure, set theoretic structure and order topological structure for the set of all S-primes on sequences of sets. We choose a well notation, the sequences of set, which makes mathematical reasoning itself easier, or even purely mechanical. Then we obtain a formal proof of the open problem about Mersenne composites.

In general, we may discuss Shophe German primes of the form $x,kx+c$ , then treat another prime problems, in this paper we do not discuss them.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	GIMPS Project Discovers Largest Known Prime Number: . Mersenne Research, Inc. https://www.mersenne.org/primes/press/M77232917.htm
[2]	Tao, T. (2007) Open Question: The Parity Problem in Sieve Theory. http://terrytao.wordpress.com/2007/06/05/open-question-the-parity-problem-in-sieve-theory
[3]	Davis, S. (2014) Arithmetical Sequences for the Exponents of Composite Mersenne Numbers. Notes on Number Theory and Discrete Mathematics, 20, 19-26.
[4]	Caldwell, C.K. Proof of a Result of Euler and Lagrange on Mersenne Divisors. http://primes.utm.edu/notes/proofs/MerDiv2.html
[5]	Liu, F.S. (2011) On the Sophie Germain Prime Conjecture. WSEAS Transactions on Mathematics, 10, 421-430.
[6]	Harrison, J. (2008) Formal Proof—Theory and Practice. Notices of AMS. http://www.ams.org/notices/200811/tx081101395p.pdf
[7]	Kuratowsky, K. and Mostowsky, A. (1976) Set Theory, with an Introduction to Descriptive Set Theory. North-Holland Publishing, 118-120.
[8]	Hazewinkel, M. Encyclopaedia of Mathematics, Limit. http://eom.springer.de/l/l058820.htm
[9]	Munkres, J.R. (2000) Topology. 2nd Edition, Prentice Hall, Upper Saddle River, 130.