Blocking Anticyclone in the Atlantic Sector of the Arctic as an Example of an Individual Atmospheric Vortex ()
1. Introduction
Anomalies of the meteorological regime and their related hazards over the Arctic have profound effects, including the loss of life and impacts on industry, transportation, fishing, tourism, recreation, and the landscape itself (terrestrial, sea ice, and ocean). They are very often consistent with long-lived peculiarities of regional atmospheric circulation. One of the most intense examples is so- called blocking events, when a nearly stationary circulation system can effectively “block” or redirect migratory cyclones. Such systems are evidenced by large-scale patterns in the atmospheric pressure field, which are known as blocking highs or blocking anticyclone. These blocks can remain in place for several days or even weeks, causing the areas affected by them to have the same kind of weather for an extended period. Recently, there have been several articles which demonstrate that regional weather is strongly influenced by such circulation systems (e.g., [1] [2] [3] ).
This leads to an interest in the genesis of the individual vortex (or circulation system, consisting of both anticyclone and accompanying low-pressure anomaly), persisting for a long time.
A finite region in a space with non-zero vorticity surrounded by irrotational fluid will be referred to as a vortex (or a circulation system if it includes two or several vortexes). The mechanisms that support the vortex in a quasi-steady state are not well known. A mathematical model that allows the determination of the dynamics of the individual vortex (or circulation system), considering its inter- action with the environment, does not exist. The significant challenge is the for- mulation of equations that describe the evolution in time of the vortex boundary. The deformation of the vortex could be calculated based on a contour dynamics method first developed for the Euler equations of fluid dynamics in two dimensions [4] . However, in order to advance the understanding of vortex dynamics, a number of simplifying proposals have been developed. For example, for motion in a plane, when the vorticity is concentrated to a point, we have a point vortex [5] . Another approach is related to when the vorticity is concentrated into elliptical form. While such a vortex can be deformed (stretch-shrink and rotate), the suggestion is that the elliptical shape should be maintained [6] [7] [8] [9] .
The application of contour dynamics methods is possible for much more general cases; however, the equations of shape deformation are so complex that they can only be solved numerically. This reduces the value of such methods, because contemporary numerical models can reproduce most features of flow directly, including the vortex structure. This makes it possible to delineate the vortex and then proceed to the calculation of its integrated characteristics. Using such an approach, original methods were recently developed, for example, allowing us to diagnose the vortex based on the position of its last closed isobar [10] .
The method of identification of the individual vortex (or system of vortexes) used in this study is based on an approximation of vorticity by several terms of the Fourier series embedded in the vorticity equation. The orthogonal basis functions are empirical orthogonal functions calculated from the data within the area occupied by the quasi-stable vortex. The same technique but at hemispheric scale and with a different purpose was realized by [11] . Due to the occurrence of the vortex in a prescribed area over a long period, the precise diagnosis of the vortex borders is unnecessary. This method allows us both to diagnose the vortex and to derive equations revealing the mechanism of vortex evolution. This study will be focused primarily on the maintenance of circulation system conditions, but not its onset, growth and decay stages.
The method developed to analyse an individual vortex was used in this study to investigate the strong and persistent blocking anticyclone which appeared over the European sector of the Arctic Region during the winter of 2012. This corresponded to the warmest temperatures in the Arctic over the entire history of routine meteorological observations. For example, it was the first time when air temperatures above 0˚C were registered in Franz Josef Land. Simultaneously, a large part of the Barents and Kara seas was ice-free. Detection of circulation phenomena leading to the block could provide the key to understanding the reasons for Arctic amplification [12] [13] [14] [15] .
2. Data and Diagnostic Methodology
In this study, the daily data of NCEP/NCAR reanalysis data, the daily synoptic data of Map Makers GIS Meteo, and radio sounding data from Arctic stations were examined. To characterize the typical features of large-scale circulation patterns, we use distribution of sea-level pressure maps, the main airflows in the middle and low troposphere (H500 and H925), and the average value of tem- perature in the lower 5-km layer of the troposphere.
To characterize the low-frequency variability of the atmospheric circulation, empirical orthogonal functions (EOFs) are calculated. However, unlike many previous studies, the EOFs were used not for empirical analysis but for the transformation of the partial differential equation describing the air motion to ordinary differential equations estimating the dynamics of the individual vortex. The space-time data field 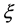 (presented by series N days long for each of M grid points of reanalysis data) can be expanded as a Fourier series using the set of functions (vectors)
(presented by series N days long for each of M grid points of reanalysis data) can be expanded as a Fourier series using the set of functions (vectors) 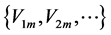 as an orthogonal basis
as an orthogonal basis
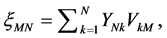 (1)
(1)
where coefficients 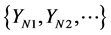 characterize the time evolution, while basis functions characterize the spatial pattern. On the basis of the well-known foundation of linear algebra, vectors
characterize the time evolution, while basis functions characterize the spatial pattern. On the basis of the well-known foundation of linear algebra, vectors 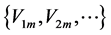 are eigenvectors of the covariance matrix:
are eigenvectors of the covariance matrix: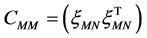 . Consequently,
. Consequently, 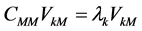 ,
, 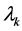 are the eigenvalues of the matrix. Expression
are the eigenvalues of the matrix. Expression 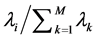 characterizes the contribution of the ith component to dispersion.
characterizes the contribution of the ith component to dispersion.
As a characteristic of the motion of air, we use the vertical component of the curl of velocity, named the vorticity. A finite region in the space filled with negative vorticity surrounded by irrotational fluid will be referred to as an anticyclone. Because we will study the large-scale peculiarities of atmospheric circulation within the extratropical region, the equation, describing the vorticity budget, can be determined using a quasi-geostrophic approach.
First, we consider the trivial expression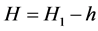 , where
, where 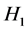 and
and 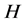 are the geopotential heights. Taking the
are the geopotential heights. Taking the 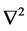 (the Laplace operator in two dimen- sions) of this expression and taking the product with
(the Laplace operator in two dimen- sions) of this expression and taking the product with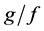 , where
, where 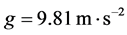 is gravity and
is gravity and 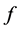 is Coriolis parameter, we have
is Coriolis parameter, we have
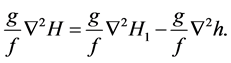 (2)
(2)
The second term on the right-hand side of Equation (2) can be replaced using the static equation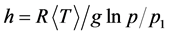 , where R is a gas constant, p and p1 are pressure on the levels, corresponding
, where R is a gas constant, p and p1 are pressure on the levels, corresponding ![]() and
and![]() , respectively,
, respectively, ![]() denotes vertically (between levels
denotes vertically (between levels ![]() and
and![]() ) averaged air temperature.
) averaged air temperature.
Taking the differential of Equation (2) with respect to time and using the determination of vorticity in the case of geostrophic motion (![]() ), we have:
), we have:
![]() (3)
(3)
This equation depicts how the vorticity at low level is dependent upon both the vorticity at higher level “1” and temperature field changes.
Let us consider that ![]() corresponds to the isobaric surface 500 hPa. Taking into consideration that the divergence in the middle troposphere is substantially less than above and below it, we conclude that the change of vorticity on this level depends primarily on its horizontal advection:
corresponds to the isobaric surface 500 hPa. Taking into consideration that the divergence in the middle troposphere is substantially less than above and below it, we conclude that the change of vorticity on this level depends primarily on its horizontal advection:
![]() (4)
(4)
To get the expression for ![]() we use the thermodynamic energy equation. A bit of algebra and it is found that Equation (3) is replaced by
we use the thermodynamic energy equation. A bit of algebra and it is found that Equation (3) is replaced by
![]() (5)
(5)
where ![]() is the temperature advection,
is the temperature advection, ![]() is vertical velocity,
is vertical velocity, ![]() is a difference between the dry adiabatic lapse rate and the vertical temperature gradient.
is a difference between the dry adiabatic lapse rate and the vertical temperature gradient. ![]() and
and![]() , where
, where ![]() is sensible heat flux near the surface,
is sensible heat flux near the surface, ![]() is the heat equivalent of precipitation,
is the heat equivalent of precipitation, ![]() is specific heat at constant pressure,
is specific heat at constant pressure, ![]() is air density.
is air density. ![]() reflects the radiation budget. Considering that spatial configurations of the radiative flux and
reflects the radiation budget. Considering that spatial configurations of the radiative flux and ![]() are approximately the same, and taking into account that
are approximately the same, and taking into account that ![]() within the anticyclone is small (especially during winter), last three terms on the right-hand side of Equation (5) can be replaced by
within the anticyclone is small (especially during winter), last three terms on the right-hand side of Equation (5) can be replaced by![]() . Last proposals allow us among other things to take into consideration the accuracy of the reanalysis data that will be used for calculations of the term
. Last proposals allow us among other things to take into consideration the accuracy of the reanalysis data that will be used for calculations of the term![]() .
.
This equation shows how low troposphere cyclogenesis is intimately related to the configuration of heat fluxes and how it is controlled by planetary waves travelling in the middle and upper atmosphere. The first term on the right-hand side represents the advection of vorticity given the planetary wave control of the circulation pattern of the low troposphere. The second term is the contribution of heat (temperature) advection due to the flow motion in the horizontal direction. The third term represents the effect of adiabatic changes. The forth term depicts diabatic changes due to vertical sensible and radiative heat fluxes [16] . Note that the wind velocity vector in the expression of heat advection connects directly to vorticity [5] ; this connection is particularly simple in the case of geostrophic motion. However, its substitution into the equation leads to a much more complex expression omitting the analytical analysis.
This equation (in another form) was originally studied by S. Petterssen [17] and was a popular tool to investigate both extratropical and tropical atmospheric circulation systems [18] [19] . In time, interest in this method waned because the models came to simulate atmospheric flow including vortices with good skill. We again turned to this technique, but with a different focus.
For the simplicity of presentation, we rewrite Equation (5) in the form:
![]() (6)
(6)
sequentially replacing each term on the right side of Equation (5) to the appropriate designation.
3. Synoptic Evidence of Winter Warming in the Arctic
During the winter of 2012, due to the exceptionally intensive inflow of heat to the Arctic in the winter and the intensification of the West Spitsbergen Current, the area of ice cover in the Barents and Kara seas was minimal compared to the entire history of routine remote observations. The air temperature was abnormally warm over the European sector of the Arctic. At the same time, the transformations of macro-scale circulation also occurred at the middle latitudes that resulted in the cold air outflow from Siberia to the warm areas of Southern Europe.
The comprehensive analysis of aerosynoptic information enabled the identification of the basic structure of the large-scale pattern of atmospheric circulation in winter 2011/12, which resulted in the abnormally warm weather in the Atlantic sector of the Arctic. This is clear in the surface map for February 8, depicting the typical situation (Figure 1(a)).
The shape of the main pressure peculiarities on the surface map (Figure 1(a)) and intensive anticyclone at the level of 500 hPa (Figure 1(b)) ensures the maintenance of heat advection and formation of a positive temperature anomaly. The 0˚C isotherm crossed 80˚N. The air temperature was positive even on Franz Josef Land and exceeded the norm by 20˚C. The increase in the average temperature values in the lower 5-km layer over the Arctic can be seen in the field of relative topography for the layer (500 - 1000) hPa. The zone of maximum values formed over the northern part of the Barents Sea (Figure 1(c)).
Warm advection to the central part of the Arctic was corroborated by the radio sounding data. As is clear from Figures 2(a)-(c), the southern, southwestern and western winds were observed on the island stations for the entire layer of radio sounding. Cold weather with temperatures of ?16˚C, ・・・, ?18˚C, light western winds in the atmospheric surface layer, and steady easterlies above 2 - 3 km were observed in Murmansk (Figure 2(d)).
4. EOF Analysis and Persistent Vortex Index
In this study, we examine the evolution of a 925-hPa vorticity. As stated in the
![]()
Figure 1. Synoptic conditions at 12:00 UTC on February 8, 2012. (a) Surface chart; (b) H500, dam; (c) Relative topography for the layer (500 - 1000) hPa, dam. The black dots in figures are the locations of the stations: (F) Franz Josef Land; (S) Svalbard; (B) Bear Island; (M) Murmansk.
![]()
![]()
Figure 2. The data of aerological soundings at Svalbard (a), Franz Josef Land (b), Bear Island (c), and Murmansk (d) stations at 12:00 UTC on February 8, 2012. In figures (standard diagrams) the red lines are the temperature curves and the turquoise lines are the dew-point curves.
previous sections, the categorization of persistent vortexes requires that an EOF analysis of vorticity field be performed. Calculations of vorticity and its EOFs (and several other values) during the entire period (from 18 January to 13 February 2012) of the blocking anticyclone being over the Northern Europe and Western Siberia (in the region: 22.5˚E - 97.5˚E and 77.5˚ - 57.5˚N-see Figure 1) were carried out. The first three EOFs (EOF1, EOF2 and EOF3, hereafter) of the 925-hPa vorticity field constitute 36%, 22% and 10% of the total variance, respectively.
Estimate of the EOF’s from a finite number of realizations will be subject to sampling errors (see, e.g., the theory and numerical example of North et al. [20] ). We calculate the EOFs over a small region and a very small time frame (only around 1 month, covering the entirety of the blocking event of interest). In such situation, the differences between consecutive eigenvalues (and eigenvectors) are sensitive to sampling errors. Fortunately, our EOF1 is stand out, accounting for a large part of the variance. Of course, it was a consequence of a special choice of region and time frame. Another limitation of the method is associated with a priori chosen boundaries of the studied area. However, we have verified that the Fourier decomposition is practically not sensitive to the choice of configuration of the area.
We will use only EOF1 to present main peculiarities of a vorticity field![]() . Indeed, EOF1 characterizes a dipole (Figure 3). This pattern bears some resemblance to anomalies observed in the atmosphere (see Figure 1(a)). Others EOF’s will characterize the noise component. Such approach allows
. Indeed, EOF1 characterizes a dipole (Figure 3). This pattern bears some resemblance to anomalies observed in the atmosphere (see Figure 1(a)). Others EOF’s will characterize the noise component. Such approach allows
![]()
Figure 3. 925-hPa vorticity anomaly representing by EOF1. Light brown contours are positive, blue contours negative (relative units).
us to decrease the influence of sampling errors retaining the main features of the studied circulation system.
A concise method for examining the temporal evolution of EOF1 is to project combinations of terms on the rhs of (5) onto EOF1. Substitution of expression (1) into Equation (5) (or Equation (6)) yields
![]() (7)
(7)
Using the property that the ![]() form an orthogonal set of basis functions, multiplication of both sides of Equation (7) by
form an orthogonal set of basis functions, multiplication of both sides of Equation (7) by ![]() yields
yields
![]() (8)
(8)
The same procedure can be realized for other EOFs; however, since their contribution to the variance is small, their participation in vortex formation appears as noise and will be taken into consideration as stochastic process.
Thus, the projection of various combinations of terms on the rhs of Equation (7) onto ![]() gives the contribution of those terms towards the tendency of the principal component of EOF1. Naturally, such an approach could be an effective tool only if the vorticity is expanded as a Fourier series using a set with only a few terms. Moreover mentioned discussed the role of sampling errors further restricts this requirement from a formal statistical point of view.
gives the contribution of those terms towards the tendency of the principal component of EOF1. Naturally, such an approach could be an effective tool only if the vorticity is expanded as a Fourier series using a set with only a few terms. Moreover mentioned discussed the role of sampling errors further restricts this requirement from a formal statistical point of view.
Therefore, the amplitudes ![]() is integrally index depicting the time behaviour of the studied blocking circulation system. Their variations together with the associated analysis of dynamics of terms on the rhs of Equation (8) allows us to obtain information about the blocking mechanisms.
is integrally index depicting the time behaviour of the studied blocking circulation system. Their variations together with the associated analysis of dynamics of terms on the rhs of Equation (8) allows us to obtain information about the blocking mechanisms.
5. Discussion
The projection of each term on the rhs of Equation (8) plus ![]() is shown in Figure 4. At different stages, the rate of change of the indicator
is shown in Figure 4. At different stages, the rate of change of the indicator ![]() are determined by a different set of factors. During the first decade, the interaction of two factors (the advection of absolute vorticity and the heat advection) plays a main role in anticyclone maintenance (reflected by dynamics of
are determined by a different set of factors. During the first decade, the interaction of two factors (the advection of absolute vorticity and the heat advection) plays a main role in anticyclone maintenance (reflected by dynamics of![]() ).
).
Taking into consideration the sign of ![]() (Figure 3), we can see that negative terms are needed on the rhs of Equation (8) to generate the negative (anticyclonic) vorticity. As seen from Figure 4, this role is played by the process of absolute vorticity advection. As explained in [21] blocking events over North Pacific region are maintained by fluxes of anticyclonic vorticity into the blocking domain by synoptic-scale eddies, the same mechanism dominates over the East European Plain during the catastrophic “Summer 2010” [22] , while North Atlantic blocking is shown to be planetary-scale dominant [23] .
(Figure 3), we can see that negative terms are needed on the rhs of Equation (8) to generate the negative (anticyclonic) vorticity. As seen from Figure 4, this role is played by the process of absolute vorticity advection. As explained in [21] blocking events over North Pacific region are maintained by fluxes of anticyclonic vorticity into the blocking domain by synoptic-scale eddies, the same mechanism dominates over the East European Plain during the catastrophic “Summer 2010” [22] , while North Atlantic blocking is shown to be planetary-scale dominant [23] .
Simultaneously (as seen from Figure 4), the influence of such forcing was overcome by the influence of heat advection. Indeed, the strong northward flow on the western part of the anticyclone turning to the right with increasing altitude (due to baroclinicity) provides the warm air penetration in the interior of
the anticyclone. This term contributes to decreasing anticyclonic vorticity and thus will act opposite to the advection of the middle-tropospheric vorticity.
Sometimes, the cooling effect (over a cold surface over land), presented by the term![]() , favours anticyclone development (see Figure 4), but its role is minor compare to the factors discussed earlier.
, favours anticyclone development (see Figure 4), but its role is minor compare to the factors discussed earlier.
During the second decade the process of absolute vorticity advection again generates the negative vorticity, however now its compensation by the heat advection is weaker and ![]() increases.
increases.
The effect of adiabatic changes is small, and we can therefore assume that it does not play an important role. It can be explained by both the temperature gradients not being much different from the dry adiabatic value and the vertical velocity being small.
The restructuration of the atmospheric circulation began during the third decade (the first decade of February, 2012), and the signs and roles of ![]() and
and ![]() were exchanged (see Figure 4). As a result, the blocking anticyclone was destroyed and the western flow reinstated.
were exchanged (see Figure 4). As a result, the blocking anticyclone was destroyed and the western flow reinstated.
The scheme of the Arctic blocking anticyclone dynamics (depicting by the![]() ) is presented in Figure 5. The near-balanced interaction of two processes determines the most important features of this circulation system. The first of them is the vorticity advection in the middle troposphere acting as external
) is presented in Figure 5. The near-balanced interaction of two processes determines the most important features of this circulation system. The first of them is the vorticity advection in the middle troposphere acting as external
![]()
Figure 5. Schematic representations of blocking system, denoting by indexes ![]() (see text). Thick lines and thin lines depict main and minor effects, consequently. forcing denotes external influence on circulation system due to both planetary wave control and heat advection (depending on spatial distribution of temperature within and surrounding the area where the anticyclone is located); feedbacks depict different mechanisms of feedbacks produced by the wind field connecting with the vorticity. Non-linear interactions between
(see text). Thick lines and thin lines depict main and minor effects, consequently. forcing denotes external influence on circulation system due to both planetary wave control and heat advection (depending on spatial distribution of temperature within and surrounding the area where the anticyclone is located); feedbacks depict different mechanisms of feedbacks produced by the wind field connecting with the vorticity. Non-linear interactions between ![]() and other EOF’s are carried out by the wind field connecting with the vorticity.
and other EOF’s are carried out by the wind field connecting with the vorticity.
forcing providing the planetary wave control for arctic-subarctic circulation system. The second is the influence of the heat advection. It acts at least partially as an external forcing depends on temperature anomalies located outside of the region of interest. On the other hand, it is a feedback mechanism due to the dependence of the velocity field from the vorticity distribution which ensures that velocity is uniquely determined by![]() . Here we have to take into account a roles of neglected terms in the series (1), which could be formulated as additional equations to Equation (8) if accuracy of our data allowed clear separate the consecutive EOF’s. To mimic their effect we hypothetically propose that their influence can be represented by additive noise. The diabatic factor works as a feedback mechanism, playing a role stabilizing or destabilizing.
. Here we have to take into account a roles of neglected terms in the series (1), which could be formulated as additional equations to Equation (8) if accuracy of our data allowed clear separate the consecutive EOF’s. To mimic their effect we hypothetically propose that their influence can be represented by additive noise. The diabatic factor works as a feedback mechanism, playing a role stabilizing or destabilizing.
6. Conclusions
In this study, the blocking anticyclone, which occurred over the Arctic region during part of winter 2012, was used to assess a new method that allows the development of the low-order model of an individual vortex (or circulation system).
This key result was obtained by projecting composites of terms in the vorticity tendency equation onto particular vorticity EOF1. This EOF1 denotes an arctic- subarctic circulation system including the blocking anticyclone. The projection of these terms is a measure of their contribution to the tendency of the principal components of the EOF1, marked as index![]() , which is the integrated indicator of individual vortex dynamics. The near-balanced effects of vorticity advection and heat advection determine the mostly important features. Minor peculiarities are determined by the action of diabatic processes.
, which is the integrated indicator of individual vortex dynamics. The near-balanced effects of vorticity advection and heat advection determine the mostly important features. Minor peculiarities are determined by the action of diabatic processes.
We stress that result of this study concerns only one example of a blocking situation. Further study of other individual vortices (or circulation systems) located in different regions is needed to expand our findings to other objects.
Acknowledgements
Support of this work is provided by both the Russian Foundation for Basic Research (grant NO. 14-37-00038) and the Lomonosow Moscow State University (grant NO. АААА-А16-116032810086-4).