A New Augmented Lagrangian Objective Penalty Function for Constrained Optimization Problems ()
1. Introduction
Augmented Lagrangian penalty functions are effective approaches to inequality constrained optimization. Their main idea is to transform a constrained optimization problem into a sequence of unconstrained optimization problems that are easier to solve. Theories on and algorithms of Lagrangian penalty function were introduced in Du’s et al. works [1] . Many researchers have tried to find alternative augmented Lagrangian functions. Many literatures on augmented Lagrangian (penalty) functions have been published from both theoretical and practical aspects (see [2] - [8] ), whose key concerns cover zero gap of dual, existence of saddle point, exactness, algorithm and so on.
All augmented Lagrangian functions consist of two parts, a Lagrangian function with a Lagrangian parameter and a penalty function with a penalty parameter (see [2] - [8] ). Dual and saddle point is the key concerns of augmented Lagrangian function. Moreover, zero gap of Lagrangian function’s dual is true only for convex programming and augmented Lagrangian function. Therefore, augmented Lagrangian function algorithms solve a sequence of constrained optimization problems by taking differential Lagrangian parameters and penalty parameters in [2] [3] [4] [5] . Lucidi [6] and Di Pillo et al. [7] obtained some results of exact augmented Lagrangian function, but numerical results were not given. R. S. Burachik and C. Y. Kaya gave an augmented Lagrangian scheme for a general optimization problem, and established for this update primal-dual convergence the augmented penalty method in [8] . However, when it comes to computation, to apply these methods, lots of Lagrangian parameters or penalty parameters need to be adjusted to solve some unconstrained optimization dual problems, which make it difficult to obtain an optimization solution to the original problem. Hence, it is meaningful to study a novel augmented Lagrangian function method.
In recent years, the penalty function method with an objective penalty parameter has been discussed in [9] - [16] . Burke [12] considered a more general type. Fiacco and McCormick [13] gave a general introduction to sequential unconstrained minimization techniques. Mauricio and Maculan [14] discussed a Boolean penalty method for zero-one nonlinear programming. Meng et al. [15] studied a general objective penalty function method. Furthermore, Meng et al. studied properties of dual and saddle points of the augmented Lagrangian objective penalty function in [16] . Here, a new augmented Lagrangian objective penalty function which differs from the one in [16] is studied. Some important results similar to those of the augmented Lagrangian objective penalty function in [16] are obtained.
The main conclusions of this paper include that the optimal target value of the dual problem and the optimal target value of the original problem is zero gap, and saddle point is equivalent to the KKT condition of the original problem under the convexity conditions. A global algorithm and its convergence are presented. The remainder of this paper is organized as follows. In Section 2, an augmented Lagrangian objective penalty function is defined, its dual properties are proved, and an algorithm to find a global solution to the original problem (P) with convergence is presented. In Section 3, conclusions are given.
2. Augmented Lagrangian Objective Penalty Function
In this paper the following mathematical programming of inequality constrained optimization problem is considered:

where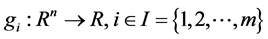 . The feasible set of (P) is denoted by
. The feasible set of (P) is denoted by

Let functions 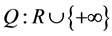 be a monotonically increasing functions satisfying
be a monotonically increasing functions satisfying
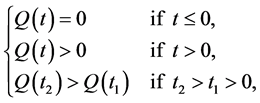
respectively. For example, 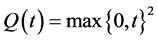 meet the requirement.
meet the requirement.
The augmented Lagrangian objective penalty function is defined as:
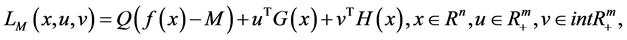 (1)
(1)
where 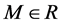 is the objective parameter, u is the Lagrangian parameter,
is the objective parameter, u is the Lagrangian parameter, 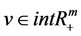 is the penalty parameter,
is the penalty parameter, 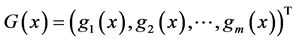 and
and  with
with  and
and
When , it is clear that
, it is clear that 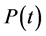 is smooth. Define functions:
is smooth. Define functions:
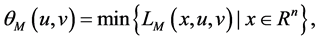 (2)
(2)
 (3)
(3)
Define the augmented Lagrangian dual problem:
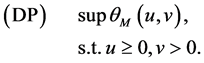
When![]() , we have
, we have
![]()
By (3), we have
![]() (4)
(4)
According to (1), we have![]() , for
, for![]() . Let
. Let![]() , then we have
, then we have![]() . So,
. So,![]() . Hence,
. Hence,
![]() (5)
(5)
Theorem 1. Let x be a feasible solution to (P), and u,v be a feasible solution to (DP). Then
![]() (6)
(6)
Proof. According to the assumption, we have
![]()
and
![]()
Corollary 2.1. Let![]() . Let
. Let ![]() be an optimal solution to (P), and
be an optimal solution to (P), and ![]() be an optimal solution to (DP). Then
be an optimal solution to (DP). Then
![]() (7)
(7)
By (5), if ![]() is an optimal solution to
is an optimal solution to![]() , then
, then ![]() is an optimal solution to (P) for
is an optimal solution to (P) for![]() . We have
. We have
![]() (8)
(8)
and know that ![]() is an optimal solution to (DP) if
is an optimal solution to (DP) if ![]() is an optimal solution to
is an optimal solution to![]() . By Corollary 2.1 we have
. By Corollary 2.1 we have
![]() (9)
(9)
A saddle point ![]() of
of ![]() is defined by
is defined by
![]() (10)
(10)
By (10), the saddle point shows the connection between the dual problem and the original problem. The optimal solution to the original problem can be obtained by the optimal solution to the dual problem and the zero gap exists in Theorem 2. The following Theorems 3 and Theorem 4 show that under the condition of convexity, saddle points are equivalent to the optimality conditions of the original problem. By (10), we have
![]()
Hence, we have the following theorems.
Theorem 2. Let![]() . Then,
. Then, ![]() is a saddle point of
is a saddle point of
![]() if and only if
if and only if ![]() is an optimal solution to (P) and
is an optimal solution to (P) and ![]() is an optimal solution to (DP) with
is an optimal solution to (DP) with![]() .
.
Theorem 3. Let ![]() be differentiable and
be differentiable and![]() . Let
. Let ![]() for
for ![]() and
and ![]() for
for![]() . If
. If ![]() is a saddle point of
is a saddle point of![]() , then,
, then, ![]() satisfies the first-order Karush-Kuhn-Tucker (KKT) condition.
satisfies the first-order Karush-Kuhn-Tucker (KKT) condition.
Proof. According to the assumption, ![]() is a saddle point of
is a saddle point of![]() , then, for any
, then, for any ![]()
![]() (11)
(11)
and
![]() (12)
(12)
where
![]()
And there are ![]() and
and ![]() such that
such that
![]() (13)
(13)
![]() (14)
(14)
![]() (15)
(15)
![]() (16)
(16)
By (12)-(16), let![]() , then we have
, then we have
![]()
![]()
For ![]() it is clear that (1) is equivalent to the following
it is clear that (1) is equivalent to the following
![]() (17)
(17)
Clearly, if![]() , then
, then![]() . We have that
. We have that ![]() if
if![]() .
.
Theorem 4. Let![]() .
. ![]() are convex and diffe-
are convex and diffe-
rentiable. Let ![]() for
for ![]() and
and ![]() for
for![]() . If
. If ![]() satisfies the first-order Karush-Kuhn-Tucker (KKT) condition, then
satisfies the first-order Karush-Kuhn-Tucker (KKT) condition, then ![]() is a saddle point of
is a saddle point of ![]() for any
for any![]() .
.
Proof. Let any![]() . According to the assumption,
. According to the assumption, ![]() is convex and differentiable on x by (17). We have
is convex and differentiable on x by (17). We have![]() ,
, ![]() and
and
![]()
On the other hand, when ![]() satisfies the first-order Karush-Kuhn- Tucker (KKT) condition, then
satisfies the first-order Karush-Kuhn- Tucker (KKT) condition, then![]() ,
, ![]() and
and ![]() . By the definition of
. By the definition of![]() , we know that
, we know that ![]() for
for![]() . So, for any
. So, for any ![]() and
and![]() , we have
, we have
![]()
Example 2.1 Consider the problem:
![]()
When![]() , the augmented Lagrangian objective penalty function is given by
, the augmented Lagrangian objective penalty function is given by
![]()
The optimal solution to ![]() is
is ![]() for
for ![]() and
and![]() . For
. For![]() , some
, some ![]() and
and![]() , it is clear that
, it is clear that
![]()
holds. Then ![]() is a saddle point of
is a saddle point of![]() .
.
Example 2.1 shows that the augmented Lagrangian objective penalty function can be as good in terms of the exactness as the traditional exact penalty function.
For any given![]() , define the following problem as
, define the following problem as
![]()
In Example 2.1, ![]() is an optimal solution to (P(M,u,v)). When
is an optimal solution to (P(M,u,v)). When![]() ,
,![]() .
.
Now, a generic algorithm is developed to compute a globally optimal solution to (P) which is similar to the algorithm in [15] . The algorithm solves the problem (P(M,u,v)) sequentially and is called Augmented Lagrangian Objective Penalty Function Algorithm (ALOPFA Algorithm for short).
ALOPFA Algorithm:
Step 1: Choose![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and![]() .
.
Step 2: Solve![]() . Let
. Let ![]() be a global minimizer.
be a global minimizer.
Step 3: If ![]() is not feasible to (P), let
is not feasible to (P), let![]() ,
, ![]() ,
, ![]() ,
, ![]() and go to Step 2.
and go to Step 2.
Otherwise, stop and ![]() is an approximate solution to (P).
is an approximate solution to (P).
The convergence of the ALOPFA algorithm is proved in the following theorem. Let
![]() (18)
(18)
which is called a Q-level set. We say that ![]() is bounded if, for any given
is bounded if, for any given ![]() and a convergent sequence
and a convergent sequence![]() ,
, ![]() is bounded.
is bounded.
Theorem 5. Let ![]() exist. Suppose that Q and
exist. Suppose that Q and ![]() are continuous, and the Q-level set
are continuous, and the Q-level set ![]() is bounded. Let
is bounded. Let ![]() be the sequence generated by the ALOPFA Algorithm. If
be the sequence generated by the ALOPFA Algorithm. If ![]() is an infinite sequence with
is an infinite sequence with![]() , then
, then ![]() is bounded and any limit point of it is an optimal solution to (P).
is bounded and any limit point of it is an optimal solution to (P).
Proof. The sequence ![]() is bounded is shown first. Since
is bounded is shown first. Since ![]() is an optimal solution to
is an optimal solution to![]() ,
,
![]()
because ![]() for
for![]() . We have
. We have
![]() , then there is a bound of sequence
, then there is a bound of sequence![]() , because
, because ![]() has the optimal solution. Therefore, there a
has the optimal solution. Therefore, there a ![]() such that
such that ![]() for
for![]() ,
, ![]() and
and ![]() as
as![]() , and it is concluded that there is some
, and it is concluded that there is some ![]() such that
such that
![]()
Since the Q-level set ![]() is bounded, the sequence
is bounded, the sequence ![]() is bounded.
is bounded.
Without loss of generality, we assume![]() . Let
. Let ![]() be an optimal solution to (P). Note that
be an optimal solution to (P). Note that
![]()
Letting ![]() in the above inequality, we obtain that
in the above inequality, we obtain that
![]()
which implies![]() . Therefore,
. Therefore, ![]() is an optimal solution to (P).
is an optimal solution to (P).
Theorem 5 means that the ALOPFA Algorithm has global convergence in theory. When v is taken big enough, an approximate solution to (P) by the ALOPFA Algorithm is obtained.
3. Conclusion
This paper discusses dual properties and algorithm of an augmented Lagrangian penalty function for constrained optimization problems. The zero gap of the dual problem based on the augmented Lagrangian objective penalty function for constrained optimization problems is proved. Under some conditions, the saddle point of the augmented Lagrangian objective penalty function i.e. equivalent to the first-order Karush-Kuhn-Tucker (KKT) condition. Based on the augmented Lagrangian objective penalty function, an algorithm is presented for finding a global solution to (P) and its global convergence is also proved under some conditions. There are still some problems that need further study for the augmented Lagrangian objective penalty function, for example, the local algorithm, exactness, and so on.
Acknowledgements
We thank the editor and the referees for their comments. This research is supported by the National Natural Science Foundation of China under Grant No. 11271329 and the Natural Science Foundation of Ningbo City under Grant No. 2016A610043 and the Natural Science Foundation of Zhejiang Province under Grant No. LY15G010007.