Physics on the Adiabatically Changed Finslerian Manifold and Cosmology ()
1. Introduction
The problem of formulation of general theory which could naturally unify General Relativity (GR) and Quantum Theory (QT) is of most fundamental and actual problem of modern physics. But to resolve this problem, we should first to know what the Planck constant is. This is the question which opens the door and allows us to find unified theory for all branches of physics. To obtain this key we have first to have in mind some important facts.
1) In quantum mechanics, Planck constant always appears together with derivatives in the same power. This fact clearly points out on the possible relation between Planck constant and geometry.
2) Einstein [1] and later Debye [2] have shown from thermodynamical approach that electromagnetic field is quantized alone, without any assumption on the nature of oscillators. So this is another hint that it should be quantized from geometry, without axiomatic introduction of the wave function.
3) Recently the cornerstone result was announced [3] in respect to the quantization at very small scales. It was found that at the small scales a quantum system behaves as a classical one (see paper [3] for details). This result also argues that QT is pure geometrical phenomenon and it disappears at small scales when geometry becomes to be approximately Euclidean.
4) In 2011, Zhotikov showed [4] that quantum postulates of Bohr and quantization rules of Bohr-Sommerfeld, follow directly from the geometric structure of space-time.
5) Recently, we have published the paper in which we clearly points out the geometrical origin of the Planck constant [5] . In this paper, we have shown that the Planck constant is adiabatic invariant of electromagnetic field on the adiabatically changed Finslerian manifold. From this fact, the variation of the Planck constant on the time directly follows (and hence variations of fundamental constants, for example variation of the fine structure constant, due to adiabatically changed geometry [5] [6] ).
On the one hand, we have these serious arguments for the geometric origin of quantization, but on the other hand, we have also serious problems with Riemannian geometry. General relativity was created as theory on (pseudo-) Riemannian manifold (we will use farther in this paper “Riemannian” instead of “pseudo-Remannian”). Such choice was not favored by some serious arguments but only by the fact the real geometry is curved. Metric tensor
in this case depends only on the coordinates and this fact applies some restrictions on the theory, and leads to the serious problem with singularity. However, as it follows from experiments on measurement of the cosmological constant, our Uni- verse expands with acceleration and for this reason complete geometry of Finsler should be favoured. On the Finslerian manifold, the metric tensor
depends not only on coordinates, but also on velocities and (as it will be shown in this paper) this fact allows us to introduce the cosmological constant in natural way and to calculate from geometry correct value of the Planck constant, unify gravity, electrodynamics and QT. The Hubble constant, cosmological constant, quantization and much more follow from the Finsler geometry in a natural way and we can conclude that Finsler geometry naturally complies with all observational data.
In this paper, we also obtain classical equations of motion for a system on the manyfold with adiabatically changed geometry and supplied by Finslerian metrical function
. We show how the Planck’s constant naturally appears from geometry and, within the (3 + 1) formalism, we write an exact relation between the Planck constant on the one hand and scalar curvature and cosmological constant on the other hand.
We show how the classical electromagnetic field is naturally quantized due to existence of adiabatic invariant of the field on adiabatically changed Finslerian manifold.
Finally, we write equations of electrodynamics, which classically (geometrically) describe quantization of electromagnetic field (and hence of any electromagnetically interacting system). To illustrate how it works, we clearly considered two important particular cases which describe these equations: i) case of free electromagnetic field, when quantization appears from geometry and leads to losses of energy as photon propagates (so called cosmological redshift), and ii) the Aharonov-Bohm effects, which immediately follow from obtained electrodynamic equations.
All-around in this paper we suppose that Latin indexes
and greek
. Signature of metric is
.
2. Adiabatic Invariant and General Formalism
In classical physics the equations of motion follow immediately from the relation
, where
is action of matter and
is a constant or zero. By varying this equation we obtain usual classical Hamilton (or Lagrange-Euler) equations [7] .
In the case of General Relativity we put into the right hand part of Equation (1) the only invariant we have in pseudo-Riemannian geometry―scalar curvature
of the manifold and this way obtain the Einstein equations.
More general case appears when we consider a manifold supplied by Finslerian metric. The case of static Finslerian manifold is well studied and can be found for example in textbooks [8] [9] and papers [10] [11] . We should also mention here very interesting discussion regarding unusual properties of equations of motion on Finsler manifold suggested in [12] . Let us consider what happens in general case, when the right-hand term of Equation (1) contains some adiabatically changed parameters which characterize the Finslerian manifold, i.e. when the geometry of the manifold is changed adiabatically on time.
Let
be an 3-dimensional, class
manifold characterized by scalar curvature
in the point
, where
is a local coordinate on an open subset
. Let also suppose
be supplied by Finsler metric
and write a 1-parameter family of hypersurfaces on the
defined by equation
(1)
Here
stay for matter action and
corresponds to the 1-parameter family of the adiabatically changed hypersurfaces on the
. Our more general case differs from that examined in [8] by the fact that now hypersurface is changed adiabatically.
Our aim is to write the geodesic equations (Hamilton or Lagrange-Euler equations) for this general case. By varying (1)
(2)
we immediately obtain Hamilton-like equations
(3)
and
(4)
One can see that due to expansion of the Universe (adiabatic changes of right hand term in (1)) there appears an additional force in the Equation (3) and an additional velocity in (4), which we naturally can attribute to cosmological constant (acceleration) and to the Hubble constant (
). It actually corresponds to the fact that absolutely closed systems do not exist and those additional terms appear due to adiabatic changes of geometry (changes of metric tensor) which take place because of the Universe expansion.
Absolutely the same way we can write equations of Lagrange-Euler by varying (1):
(5)
As one can see in right part of this equation again appear two additional terms due to expansion of the Universe (due to changing of geometry of the manifold, as the system under consideration is moving).
3. Exact Planck’s Constant Value and Quantization of Electromagnetic Field
Let us calculate value of the Planck constant from the parameters which characterize the Finslerian manifold. Consider a generalized system distributed over volume. Let
and
be respectively tangent and cotangent bundles on
, where
and
are covariant and contravariant components of corresponding momentum.
We are interested here in the variation of the photon momentum due to adiabatic change of geometry of
. This variation can be obtained directly from the geometry [6] , but also from Einstein’s equations. Variation of the momentum density of our system due to changes of M, in unit volume summed over all directions is given by expression
(6)
Here, the scalar curvature
and
is the radius of curvature (we note here that we are interested in the evolution of the electromagnetic field, which is described by a tensor of rank = 2. Such tensors are known to correspond to a 2D surface). In this section, and later in this article we are interested in the electromagnetic field, or more precisely―its variation due to the change of the metric. Therefore, we identify the coordinate
with the size of the field resonator (a “box”). Accordingly, the value
will characterize the speed of change for this “box” due to adiabatic changes in geometry of the manifold M.
It is well known that on the Finsler manifold the metric tensor depends on
and
for this reason the momentum
also depends on
and
. Let us assume that the geometry changes are adiabatic and due to this fact we can represent
as
, where
and
are constant. In this case we have
and, hence (see Equation (6))
too. So we can write
(7)
here we note that
where
is the Hubble constant.
But by taking into account that (see [6] )
(8)
one can write
(9)
Let us consider variation of Hubble constant.
From the relation
we can find
(10)
or
(11)
But the only cosmological acceleration we have experimentally measured is that, associated with the cosmological constant
, so we can write for this variation
(12)
Substituting these expressions into (7) we find
(13)
or taking into account that for electromagnetic field
and by changing volume from the spherical coordinates to the euclidean ones, we obtain
(14)
This is a variation of momentum (in unit volume in 3 directions) due to adiabatically changed geometry, written for our generalized system localized on the Finslerian manifold.
Now we are ready to write a complete adiabatic invariant for a free propagating electromagnetic field. The components of the 4-momentum
of free electromagnetic field propagating on the Finslerian manifold with adiabatically changed geometry are varied on time. This variation proceeds adiabatically and can be considered as linear function i.e. for energy
of the field, for example, we have
(15)
so, the adiabatic invariant we are interested in is given by the expression
(16)
But
(17)
By substituting (14) into (16) we can write finally (we divide
by factor 3 because in the case of the electromagnetic plane wave, we are interesting only in one direction of the momentum)
(18)
so, by taking into account
,
(see comments made before and also [6] ), measured values of
and
[13] we have for this adiabatic invariant
for one second and in cubic centimeter, as it should be. In the same way we can obtain similar relations for other components of 4-momentum:
(19)
(there is no summation over
in this relation and for the photon propagating in direction
the components
). In the case of plane electromag- netic wave, introduced here 4-vector
has components in unit volume:
And for general case we can write
(20)
Here the adiabatic invariant for electromagnetic field (Planck constant), which depends clearly on the parameters of the manifold
and
(and consequently depends on time) is:
(21)
that gives for unit time and unit volume at present epoch
as it was mentioned above. From this relation it is easy to see that the Planck constant depends on time as
.
3.1. Hilbert Integral
Now let’s consider integral of Hilbert for particular case of the free electromagnetic field propagating along geodesic on the adiabatically changed Finslerian manifold:
(22)
where
is 4-momentum of the field,
is generalized coordinate and right hand term
, as before, corresponds to the changing of the 1-parameter family of hypersurfaces due to adiabatic variation of geometry as system under consideration is moving on
. For electromagnetic field described by Lagrangian
we have from (22)
(23)
By taking into account that tensor of energy-momentum is
(24)
we can write for propagating classical electromagnetic field
(25)
If the field propagates in the direction
, than electric field
and magnetic field
. So the only non-zero components of the field tensor
are
;
and hence
, where for the plane wave we have
and
.
In this case for the 00-component, for example, by taking into account (18) and after elementary integration we obtain
(26)
Similar relations one can write for other components.
So, as one can see the classical electromagnetic field is quantized due to adiabatic variation of the Finslerian manifold and we do not need some artificial methods to quantize it.
3.2. Variation of the Fine Structure Constant
As it was shown before [6] even on the adiabatically changed Riemannian manifold the value of the fine structure constant is changed adiabatically on time. This variation appears due to a change in the metric of space, in which the atom is localized. In the case of Finslerian manifold this variation is smaller by factor 2/3 due to the presence of the cosmological constant. To show this let’s start from (14). For one direction (divided by factor 3) we have from (14):
(27)
But the fine structure constant is
where
is electron velocity at the first Bohr orbit. Momentum in this case we can write as
(28)
so
(29)
and
(30)
that give us value
(for 1 second), 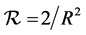 ,
(see [6] ),
and
).
,
(see [6] ),
and
).
4. Electrodynamics on the Finslerian Manifold
In Riemannian geometry, the first pair of equations of electrodynamics follows directly from the properties of the field tensor.
(31)
where
(32)
And for this reason (
) the first pair of equations on Riemannian manifold with constant scalar curvature is
(33)
On the Finsler manifold, we can obtain the first pair in the same way, but in this case the field tensor is
(34)
where covariant differentials
include now terms with the Cartan connections
like this
and also
. In the most im-
portant case, we are interested in, when the scalar curvature is small and the metric tensor has spatial structure described by the Robertson-Walker metric, the additional terms
and
in covariant derivative can be evaluated easily as
(here
is the inverse radius of scalar curvature at the point of observation) so we have
(35)
where our estimation for the small components consist
.
As one can see these components probably will be significant only in the vicinity of black holes and can be omitted in our present consideration.
For this reason the first pair of the equations can be written as
(36)
or, by taking into account our estimations discussed above, we can write
(37)
So one can see that the first pair of electrodynamic equations remains to be the first pair of the Maxwell equations with high precision.
The second pair of equations of electrodynamics follows directly from variation of functional (1) if we consider a charge characterized by 4-current
, and the electromagnetic field on the Finslerian manifold:
(38)
Here
as before, corresponds to the family of the hypersurfaces on the expanded manifold. By varying
we have
(39)
here we put
instead of
because, as we have seen, small additional terms corresponding to small components of
are insignificant in the case of Robertson-Walker metric. Integrating the second term by parts, we obtain
(40)
By varying
we have (see Equations (16)-(20))
(41)
where, as it was shown before,
in unit volume (here
is the Planck constant) and
is a 4-volume. The equations under discussion one can write as follows
(42)
or finally
(43)
(there is no summation over
here).
This is the second pair of equations of electrodynamics on the adiabatically changed Finslerian manifold. The bounded electromagnetic field (second term) in this case is explicitly included into consideration, as it takes place in the case of Bohmian formalism when this field appears in QT as quantum potential (see [14] for details and also results of paper [15] ). It is easy to see that when the Planck constant tends to zero, the expression (43) (as it should be) is converted into the Maxwell equations. (Especially emphasize here that in this extreme case, the topology becomes simple, space is isotropic, flat and described by the Minkowski geometry). Let us consider two important cases which immediately follow from these equations.
4.1. Cosmological Redshift
It is well known that as the photon propagates through expanding universe its frequency (or wave length) is changed. This loss of energy by free electromagnetic field, named as cosmological redshift, appears in our equations by natural way as losses of the energy by photon due to adiabatically changed geometry of manifold.
(44)
(there is no summation over
).
The meaning of these equations is most obvious if we put
. In this case, the left side will be the electromagnetic field energy loss with time, and the right side became
―small value associated with the geometry of the universe (see expression (18)), i.e.
4.2. The Aharonov-Bohm Effects
Another important case that follows directly from the second pair of equations is the Aharonov-Bohm effects. As it is known, a necessary condition for the existence of the Aharonov-Bohm (AB) effects is the presence, in the overall structure of the equations, of the “zero field” potentials which cannot be removed by gauge transformations and they do not create electromagnetic fields [16] [17] . These “zero-potentials” are the result of “non-trivial topology” of the area on which the particle moves [16] [18] [19] . Such a situation arises in electrodynamics of anisotropic media where the structure of Maxwell’s equations eliminates the possibility of satisfying the boundary conditions. To satisfy regularly the boundary conditions in anisotropic media, usually the zero-potential is introduced, which do not create electromagnetic fields (see [16] and references there- in). In the case of adiabatically expanding Finslerian manifold, the anisotropy of space occurs for any moving body automatically as right part of Equaiton (43). Therefore, it is safe to say that in the case of AB effects we are dealing directly with the anisotropy of space, which appears due to adiabatically changed Finslerian manifold as the particle moves along its trajectory. In this case, the role of the zero potentials (which do not generate electromagnetic fields) performs variable geometry of space as it follows directly from (43).
In absence of electric and magnetic fields en route of propagation of the particle under consideration, the second term disappears (but it still take place inside of the solenoid and affects our particle: “In spite of the fact that the magnetic field vanishes out of the solenoid, the phase shift in the wave functions is proportional to the corresponding magnetic flux inside of the solenoid” [20] ) and we obtain (we neglect here by the small term
)
(45)
but
(here
is charge density and
is 3-velocity) so if we put
and remember that
(for this reason
and
) we obtain by using the Gauss theorem
(48)
These equations describe the electric and magnetic effects of Aharonov-Bohm (here
and
are fixed). Namely for
we have for the phase variation
(49)
electric effect of Aharonov-Bohm, and when
(here
) we have relation
(50)
describes magnetic effect of Aharonov-Bohm.
To conclude this part we would like to stress again that whereas the bounded field (second term in (43)) do not appears in these relations, it actually affects the moving particle through potentials
[20] and this bounded field corresponds to quantum potential in the Bohmian formalism [14] [15] .
5. Complete Theory
In previous part we have obtained electrodynamic equations. They are applied in the case when the movement of charge (or 4-current
) is defined. To construct self-consistent theory we should treat
as variable from the beginning.
We consider now a charge characterized by 4-current
, and the electromagnetic field on the Finslerian manifold:
(51)
Here
as before corresponds to family of the hypersurfaces on the expanded manifold. In complete form, when
, we have the action
(52)
which describes quantum properties of our system. It is clear there are a lot of different systems, particular cases and applications which can not be considered here because of their huge amount. For this reason let us consider here the hydrogen atom as an example. In order to coincide with the Schrödinger formulation of quantum mechanics, we should neglect the third term in (52) which corresponds to quantum potential [14] [15] in Bohmian formulation, and gives the zero energy correction (for example in the case of harmonic oscillator it gives term 1/2 in expression for energy [5] [14] ). In this case by varying (52) we have
(53)
and we can write
(54)
So, finally we obtain equations of motion
(55)
By taking into account that classical period for orbital movement of electron is
(56)
in classical limit
the straightforward calculations give the energy for first Bohr orbit, obtained from classical electrodynamic on Finslerian manifold:
(57)
that coincides with quantum calculations. Relativistic corrections are obvious and follow directly from (55).
6. Conclusions
In this paper, we confirm our previous result [5] that Planck constant is adiabatic invariant of electromagnetic field propagating on the adiabatically changed Finslerian manifold. Direct calculation of the Planck constant value made from cosmological parameters gives
that is in excellent agreement with the measured value. We also confirm that Planck constant (and hence other fundamental constants which depend on h) is varied on time due to changing of geometry of the manifold.
As an example we suggest a calculation of the fine structure constant variation. The obtained value consists
(for 1 second) and this variation is expected to be measured in nearest future.
We show that on the Finslerian manifold characterized by adiabatically changed geometry, classical free electromagnetic field is quantized geometrically, from the properties of the manifold.
Equations for electrodynamics on the Finslerian manifold are suggested. It is shown that quantization naturally appears from these equations and is resulted from adiabatically changed geometry of manifold. We consider in details two direct consequences of the equations―cosmological redshift of photons and effects of Aharonov-Bohm.
Finally we show appearance of quantization for the systems consisting of electromagnetic field and charged baryonic components (like atoms and molecules).
Acknowledgements
I would like to express my deepest appreciation and gratitude to my teachers: Choban E.A., Dubov V.V., Dubrovich V.K., Finkelstain B.A., Gosachinsky I.V., Ivanov V.K., Khersonsky V.K., Okunev A.A., Tichomirov S.R., Toptygin I.N., Rukolaine A.V., Varshalovich D.A., Zlatin A.N., and many others. I also have to thank my wife Olga. Thanks to her efforts, I was able to complete this work for the summer vacation 2016.