Alignment of Quasar Polarizations on Large Scales Explained by Warped Cosmic Strings. PART II: The Second Order Contribution ()
1. Introduction
In this research we extend our previous work on the relation of the alignment of quasar polarizations with warped cosmic strings [10] . Recent research in this field [22] shows peculiar correlation of quasar polarization orientations in LQGs. The alignments can be parallel or perpendicular to each other. Ever other discretizations are not excluded. We shall see that this behaviour fits in our brane world model. However, there are some peculiar issues to be addressed. A network of long cosmic strings can be characterised by a single scaling length, the persistence length of the inter-string distance. Numerical simulations have shown that the evolution of the network must be scale-invariant. It is a great challenge to prove that there is a comparable scale-invariance in the alignments of the polarization vectors of quasars. By the discovery of high-redshift super- massive black holes,  , one could extend the investigation on quasar alignment to this era. There is already a tiny indication of z-dependency in the observed quasar polarization orientations [7] . Further, the formation of small- scale closed loops of cosmic strings can disturb the energy balance of long strings. In our model this problem is overcome by the warp factor: it makes the cosmic string more massive during the evolution.
, one could extend the investigation on quasar alignment to this era. There is already a tiny indication of z-dependency in the observed quasar polarization orientations [7] . Further, the formation of small- scale closed loops of cosmic strings can disturb the energy balance of long strings. In our model this problem is overcome by the warp factor: it makes the cosmic string more massive during the evolution.
In Section 2 we outline the multiple-scale method on a warped brane world spacetime. In Section 3 we calculate the metric perturbations to second order. In Section 4 we derive the matter field equations to second order and indicate the possible relation with axially symmetric instabilities caused by radiation- reactions. In Section 5 we discuss the possible connection of the warp factor with conformal invariance. In the appendices we collected all the relevant equations in order to keep the main text readable and self-contained.
2. The Multiple-Scale Approximation on a Warped Brane World Spacetime
We will investigate vortex-like solution on a warped five-dimensional Fried- mann-Lematre-Robertson-Walker (FLRW) model in cylindrical coordinates [9] [10] :
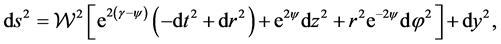 (1)
(1)
with 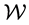 a warpfactor dependent of
a warpfactor dependent of 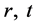 and the bulk dimension y. The self- gravitating scalar-gauge field, parameterized as
and the bulk dimension y. The self- gravitating scalar-gauge field, parameterized as
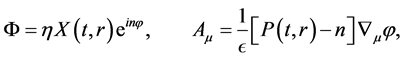 (2)
(2)
resides on the brane.  is the vacuum expectation value of the scalar field, n the winding number and
is the vacuum expectation value of the scalar field, n the winding number and  the gauge coupling constant. The winding number (number of jumps in phase of the scalar field when one goes around the flux tube) is related to the quantized flux in the Ginsberg Landau theory of super- conductivity (Abrikosov vortices) and the discrete values of the topological charge in the sin-Gordon theory. The exact solution of
the gauge coupling constant. The winding number (number of jumps in phase of the scalar field when one goes around the flux tube) is related to the quantized flux in the Ginsberg Landau theory of super- conductivity (Abrikosov vortices) and the discrete values of the topological charge in the sin-Gordon theory. The exact solution of ![]() [9] follows from the 5D Einstein equation
[9] follows from the 5D Einstein equation
![]() (3)
(3)
with![]() ,
, ![]() the brane tension and
the brane tension and![]() . The
. The ![]() is the fundamental 5D Planck mass. The scalar-gauge field equations become [4]
is the fundamental 5D Planck mass. The scalar-gauge field equations become [4]
![]() (4)
(4)
with ![]()
![]() the covariant derivative with respect to
the covariant derivative with respect to ![]() and
and ![]() the potential of the Abelian Higgs model. The star represents the complex conjugated.
the potential of the Abelian Higgs model. The star represents the complex conjugated. ![]() is the Maxwell tensor. The modified Einstein eq- uations become [20]
is the Maxwell tensor. The modified Einstein eq- uations become [20]
![]() (5)
(5)
with ![]() the Einstein tensor calculated on the brane metric
the Einstein tensor calculated on the brane metric ![]() and
and ![]() the unit vector normal to the brane. We will consider here
the unit vector normal to the brane. We will consider here![]() , so we are dealing with the RS-fine tuning condition [15] . The last two terms on the righthand side of Equation (5) represent the quadratic contribution of the energy-momentum tensor and the electric part of the five dimensional Weyl tensor respectively. All standard model fields are bound to the brane, although gravity may propagate into the extra dimension. Is is obvious, that the cosmic string can build up a huge mass
, so we are dealing with the RS-fine tuning condition [15] . The last two terms on the righthand side of Equation (5) represent the quadratic contribution of the energy-momentum tensor and the electric part of the five dimensional Weyl tensor respectively. All standard model fields are bound to the brane, although gravity may propagate into the extra dimension. Is is obvious, that the cosmic string can build up a huge mass ![]() by the warp factor and can induce massive KK-modes felt on the brane. The warp factor causes perturbations to be damped as they move away from the brane, so gravity looks four dimensional, at least perturbatively, to a brane world observer. Brane world models can also explain the acceleration of the universe without the need of a cosmological constant [18] . Disturbances can survive the natural damping by expansion of the universe due to the warp factor. This effect was also found numerically [9] .
by the warp factor and can induce massive KK-modes felt on the brane. The warp factor causes perturbations to be damped as they move away from the brane, so gravity looks four dimensional, at least perturbatively, to a brane world observer. Brane world models can also explain the acceleration of the universe without the need of a cosmological constant [18] . Disturbances can survive the natural damping by expansion of the universe due to the warp factor. This effect was also found numerically [9] .
Here we will consider the modified cosmic string features on the warped spacetime Equation (1) and use the multiple-scale approximation [23] [24] [25] in order to find partial differential equations (PDE’s) for the perturbations to second order of the metric and matter fields. This extends our previous research [10] .
Let us expand the metric field and the scalar-gauge fields in the multiple-scale scheme
![]() (6)
(6)
with ![]() the background metric and
the background metric and ![]()
![]() the background scalar and gauge fields. For the scalar field we take different winding numbers, so different magnetic flux quantization for the background field and higher order per- turbations. We define
the background scalar and gauge fields. For the scalar field we take different winding numbers, so different magnetic flux quantization for the background field and higher order per- turbations. We define ![]() and
and
![]() . So we break up the original vortex with winding number n in our case in three strings with winding numbers
. So we break up the original vortex with winding number n in our case in three strings with winding numbers ![]() and
and![]() . One can prove [26] that this breakup remains stable if the gauge to scalar mass is
. One can prove [26] that this breakup remains stable if the gauge to scalar mass is![]() . In our case stability will be guaranteed by inverse powers of the warp factor. Further, we parametrize
. In our case stability will be guaranteed by inverse powers of the warp factor. Further, we parametrize![]() , which will fulfil the highest order perturbation equation of the gauge field as we shall see. Rapid
, which will fulfil the highest order perturbation equation of the gauge field as we shall see. Rapid
perturbations occur in the direction of the wave vector![]() . We define
. We define
![]() (7)
(7)
Substituting the expansions into the effective Einstein and matter field equations, one obtains a set of PDE’s for ![]() and the scalar gauge fields
and the scalar gauge fields ![]() and
and![]() . The perturbations can be
. The perturbations can be ![]() -dependent.
-dependent.
The Einstein equations in subsequent orders of approximation become
![]() (8)
(8)
![]() (9)
(9)
![]() (10)
(10)
We will consider here the equations up to order![]() . We used the notation for the several terms in the expansion of a tensor, vector or scalar:
. We used the notation for the several terms in the expansion of a tensor, vector or scalar:
![]() . The contribution from the bulk space,
. The contribution from the bulk space, ![]() ,
,
must be calculated with the 5D Riemann tensor. If we consider![]() , i.e., the Eikonal equation (which follows from the
, i.e., the Eikonal equation (which follows from the ![]() scalar equation), then one obtains from Equation (8) a set of restrictions on
scalar equation), then one obtains from Equation (8) a set of restrictions on![]() , such as the “gauge
, such as the “gauge
condition”![]() . Let us consider as a simplified case
. Let us consider as a simplified case
![]() . Then we let survive
. Then we let survive ![]() and
and ![]() as independent first order perturbations of the metric.
as independent first order perturbations of the metric.
3. The Metric Perturbations up to Second Order
The PDE’s for the background fields ![]() and the first order perturbations
and the first order perturbations ![]() can be derived from Equation (9)and were found in [10] . By integrating Equation (10) with respect to
can be derived from Equation (9)and were found in [10] . By integrating Equation (10) with respect to![]() , one obtains
, one obtains
![]() (11)
(11)
with ![]() the period of the rapid variation. The last two terms on the right hand side of Equation (11) can be interpreted as “back-reaction” contribution of the KK-modes of the perturbative 5D graviton and can act as a cosmological constant. These equations can be used to eliminate the background fields from the first order PDE’s. One then obtains propagation equations for the first order perturbations. For completeness we collected them in appendix A. From these equations one observes that to first order there is an interaction between the high-frequency perturbations from the bulk, the matter fields on the brane and the evolution of
the period of the rapid variation. The last two terms on the right hand side of Equation (11) can be interpreted as “back-reaction” contribution of the KK-modes of the perturbative 5D graviton and can act as a cosmological constant. These equations can be used to eliminate the background fields from the first order PDE’s. One then obtains propagation equations for the first order perturbations. For completeness we collected them in appendix A. From these equations one observes that to first order there is an interaction between the high-frequency perturbations from the bulk, the matter fields on the brane and the evolution of![]() , also found in the numerical solution [9] . The bulk contribution
, also found in the numerical solution [9] . The bulk contribution ![]() is amplified by
is amplified by![]() . It is a reflection of the massive KK modes felt on the brane. The most interesting equation is the differential equation for
. It is a reflection of the massive KK modes felt on the brane. The most interesting equation is the differential equation for![]() , i.e., the
, i.e., the ![]() component, Equation (24). It triggers the
component, Equation (24). It triggers the ![]() - dependent disturbances. The
- dependent disturbances. The ![]() -term, amplified by warp factor
-term, amplified by warp factor![]() , can have extremal values on
, can have extremal values on![]() , if we choose, for example,
, if we choose, for example,![]() . We then have the term
. We then have the term![]() , which has two extremal values on
, which has two extremal values on
![]()
![]() (also found in [10] ).
(also found in [10] ).
Let us now investigate the higher order equations in![]() , i.e., Equation (10), which will provide us first order equations of
, i.e., Equation (10), which will provide us first order equations of ![]() and second order eq- uations for
and second order eq- uations for![]() . With the help of an algebraic manipulation program, one obtains, for example, the equations for
. With the help of an algebraic manipulation program, one obtains, for example, the equations for ![]() and
and![]() , were we took for the
, were we took for the
moment ![]() and
and![]() . See Appendix B.
. See Appendix B.
We observe in Equation (33) again a ![]() -term amplified by the warp factor. In the equation Equation (34) for
-term amplified by the warp factor. In the equation Equation (34) for![]() , there appears besides the term
, there appears besides the term![]() , also a
, also a ![]() -term in connection with the second order perturbation
-term in connection with the second order perturbation![]() , amplified by the warp factor. In the equation for the first order counterpart equation, i.e., Equation (24), there is only the
, amplified by the warp factor. In the equation for the first order counterpart equation, i.e., Equation (24), there is only the ![]() -term. So if we take in Equation (34) for
-term. So if we take in Equation (34) for ![]() (and
(and![]() ), then the maxima in
), then the maxima in ![]() of these two terms belonging to the perturbations of first and second order respectively, are out-of-phase. In the next section this will also become clear by considering the energy-current com- ponents of the energy momentum tensor. From Equation (33) and Equation (26) we can obtain a second order PDE for
of these two terms belonging to the perturbations of first and second order respectively, are out-of-phase. In the next section this will also become clear by considering the energy-current com- ponents of the energy momentum tensor. From Equation (33) and Equation (26) we can obtain a second order PDE for ![]() if we impose constraint conditions on
if we impose constraint conditions on ![]() or integrate Equation (33) with respect to
or integrate Equation (33) with respect to![]() . This can also be done for the other components. So we can construct with the multiple-scale method uniformly valid wavelike approximations to solutions of perturbation problems without without “resonance” interactions between the consecutive orders of perturbation theory. This result is related to the Cauchy problem. In any field theory where there is a gauge freedom (as, for example, in GRT and Maxwell theory), one has to specify gauge conditions in order to determine the dynamical evolution for some initial set of Cauchy data. In Maxwell theory one usually choose the Lorentz gauge. In GRT one has constraint equations because the system is over determined. These constraints are usually PDE’s of first order. In our approximation scheme we have Equation (8) which leads to conditions on
. This can also be done for the other components. So we can construct with the multiple-scale method uniformly valid wavelike approximations to solutions of perturbation problems without without “resonance” interactions between the consecutive orders of perturbation theory. This result is related to the Cauchy problem. In any field theory where there is a gauge freedom (as, for example, in GRT and Maxwell theory), one has to specify gauge conditions in order to determine the dynamical evolution for some initial set of Cauchy data. In Maxwell theory one usually choose the Lorentz gauge. In GRT one has constraint equations because the system is over determined. These constraints are usually PDE’s of first order. In our approximation scheme we have Equation (8) which leads to conditions on![]() . The first order equations Equations (23)-(27) can also be considered as constraint equations for the second order wave equations for
. The first order equations Equations (23)-(27) can also be considered as constraint equations for the second order wave equations for![]() , as example, in the case of
, as example, in the case of![]() . So we can construct a dynamical evolution of the system of equations which fulfil the Cauchy data.
. So we can construct a dynamical evolution of the system of equations which fulfil the Cauchy data.
We shall see in the next sections how this result can be applied in context with the recently observed alignment of the polarization vectors of quasars over large distances and the discreteness in the azimuthal dependency of the polarization axes.
4. The Matter Field Equations and the Energy-Momentum Tensor Expansion
From Equation (4) we obtain, after substituting the expansions of Equation (6), from the ![]() equations the conditions
equations the conditions ![]() and
and![]() . So we will parameterize
. So we will parameterize ![]() and
and![]() , otherwise
, otherwise ![]() must be zero. From the first order equation of the scalar field we obtain
must be zero. From the first order equation of the scalar field we obtain
![]() (12)
(12)
where we have integrated the equation with respect to![]() . On the right hand side we see again the high-frequency contribution to the field equation. In our case, this back reaction term turns out to be zero. So the first order equation is just the unperturbed equation for
. On the right hand side we see again the high-frequency contribution to the field equation. In our case, this back reaction term turns out to be zero. So the first order equation is just the unperturbed equation for![]() . See Equation (28) of Appendix A. This also holds for the equation for
. See Equation (28) of Appendix A. This also holds for the equation for![]() . See Equation (29) of appendix A. If we substitute back the integrated equations into the original equations, we then obtain the first order perturbations (for
. See Equation (29) of appendix A. If we substitute back the integrated equations into the original equations, we then obtain the first order perturbations (for![]() ). See Equation (30)-Equation (32) of Appendix A. Further, we used
). See Equation (30)-Equation (32) of Appendix A. Further, we used![]() , otherwise the real and imaginary parts of
, otherwise the real and imaginary parts of ![]() interact as the propagation progresses. Again, there appears a
interact as the propagation progresses. Again, there appears a ![]() -dependent term in the propagation equation for
-dependent term in the propagation equation for![]() , amplified by
, amplified by![]() . This deviation from axially symmetry was also found by [23] . More insight in this
. This deviation from axially symmetry was also found by [23] . More insight in this ![]() -dependency can be obtained by studying the second-order matter field equations. One obtains for
-dependency can be obtained by studying the second-order matter field equations. One obtains for ![]() and
and ![]() again first order differential equations. See Appendix B. We used the fact that the complex conjugate of the full complex second order scalar equation also must be satisfied. The appearance of the terms
again first order differential equations. See Appendix B. We used the fact that the complex conjugate of the full complex second order scalar equation also must be satisfied. The appearance of the terms ![]() and
and ![]() will contribute to the next order modes of maxima in
will contribute to the next order modes of maxima in ![]() - dependent disturbances.
- dependent disturbances.
We can obtain, as in the case of the second order metric components, again second order PDE’s for ![]() and
and ![]() by suitable constraints on
by suitable constraints on ![]() and
and ![]() or integration with respect to
or integration with respect to![]() . After some rearrangement of Equation (35) for example, we get the wave equation for
. After some rearrangement of Equation (35) for example, we get the wave equation for ![]() (after suitable constraints on
(after suitable constraints on![]() ).
).
![]() (13)
(13)
where ![]() is an expression in backgrounds fields,
is an expression in backgrounds fields, ![]() and
and![]() . We have again two periodic functions
. We have again two periodic functions ![]() and
and ![]() with fre- quency difference of a factor two and where one of the functions is amplified by
with fre- quency difference of a factor two and where one of the functions is amplified by![]() . It will be necessary to study these equations numerically in order to compare the amplitudes of these two periodic functions with those of the azimuthal-angle dependent maxima of the quasar polarization alignment.
. It will be necessary to study these equations numerically in order to compare the amplitudes of these two periodic functions with those of the azimuthal-angle dependent maxima of the quasar polarization alignment.
The second order equation for ![]() can be obtained from the sum of the t- and r-components of the second order gauge field equations.
can be obtained from the sum of the t- and r-components of the second order gauge field equations.
We can calculate the three first terms of the energy momentum tensor![]() . See Appendix C. In
. See Appendix C. In ![]() there appears, for
there appears, for ![]() and
and![]() , the terms
, the terms![]() ,
, ![]() and
and![]() , while in the first order term, Equation (41), there is only the
, while in the first order term, Equation (41), there is only the![]() . This is also true for the energy- current components
. This is also true for the energy- current components ![]() and
and![]() . In the energy momentum tensor com- ponent
. In the energy momentum tensor com- ponent ![]() there is also a term proportional
there is also a term proportional![]() . In the next order
. In the next order ![]() there will be terms proportional with higher orders of
there will be terms proportional with higher orders of![]() . These higher order terms will be suppressed by the warp factor, so the vortex will not become unstable as is the case when one breakup the vortex string in multiple flux [27] .
. These higher order terms will be suppressed by the warp factor, so the vortex will not become unstable as is the case when one breakup the vortex string in multiple flux [27] .
The most interesting behavior arises in the angular component![]() , i.e., Equation (43)-Equation (45). As already noticed by Laguna-Castillo and Matzner [5] ,
, i.e., Equation (43)-Equation (45). As already noticed by Laguna-Castillo and Matzner [5] , ![]() can alternate in sign dependent of the gauge to scalar mass. This can also happen dynamically [9] . In the next order
can alternate in sign dependent of the gauge to scalar mass. This can also happen dynamically [9] . In the next order ![]() we have the
we have the ![]() con- tribution in front of
con- tribution in front of ![]() and in the next order
and in the next order ![]() the
the ![]() contribution in front of
contribution in front of ![]() (for the chosen values of
(for the chosen values of ![]() as above). So the doubling of the frequency in obvious. From the expression for
as above). So the doubling of the frequency in obvious. From the expression for![]() , Equation (46), we see that the pressure in the z-direction is again dominated by the
, Equation (46), we see that the pressure in the z-direction is again dominated by the![]() , because the second term is suppressed by
, because the second term is suppressed by![]() . There is, however, a peculiar side effect: the term
. There is, however, a peculiar side effect: the term ![]() can change sign dynamically. A numerical solution can give a decisive answer.
can change sign dynamically. A numerical solution can give a decisive answer.
There is a relation between the phase freedom ![]() of our scalar field and the secular instability of an initially quasi-stationary axially symmetric configuration caused by radiative reaction. The small non-axially symmetric deformations turn out to be of the form
of our scalar field and the secular instability of an initially quasi-stationary axially symmetric configuration caused by radiative reaction. The small non-axially symmetric deformations turn out to be of the form ![]() with m an integer [28] . This broken symmetry, described by the inverse of the angular momentum J, is comparable with the symmetry breaking of the Higgs field considered in our model. An axially symmetric systems is invariant under rotations in two dimensions, the SO(2) group. The breaking of this symmetry can be expressed in the equatorial eccentricity. The particular orientation of the ellipsoid in the (x-y) frame can be expressed through the azimuthal angle
with m an integer [28] . This broken symmetry, described by the inverse of the angular momentum J, is comparable with the symmetry breaking of the Higgs field considered in our model. An axially symmetric systems is invariant under rotations in two dimensions, the SO(2) group. The breaking of this symmetry can be expressed in the equatorial eccentricity. The particular orientation of the ellipsoid in the (x-y) frame can be expressed through the azimuthal angle![]() . This discrete change into non-axially symmetry must be cancelled by emission of gravitational energy (and is am- plified in our model by the 5D contribution), otherwise we are saddled with a helical time coordinate,
. This discrete change into non-axially symmetry must be cancelled by emission of gravitational energy (and is am- plified in our model by the 5D contribution), otherwise we are saddled with a helical time coordinate, ![]() and must give up Lorentz invariance. This is clear from the fact that our metric will then possess a
and must give up Lorentz invariance. This is clear from the fact that our metric will then possess a ![]() term. The angular momentum in (x-y) plane is determined by the currents of the momentum density,
term. The angular momentum in (x-y) plane is determined by the currents of the momentum density, ![]() and can be calculated in our case with the off-diagonal components of
and can be calculated in our case with the off-diagonal components of ![]() of Appendix C. For example
of Appendix C. For example![]() .
.
5. Quasar Polarization Alignment and Scale-Invariance
In order to explain the recently found large-scale alignments of the polarization vectors of quasars in LQGs at cosmological redshifts ![]() by cosmic strings, it would be desirable to find a kind of scale (conformal)-invariance, because it is conjectured that cosmic string networks evolve scale-invariant just after the radiation dominated era of our universe. The intricate features of the po- larization axes alignments of the quasars in LQGs show at least a kind of co- evolution at very large scales [22] , so a study of conformal symmetry of our model could be of interest.
by cosmic strings, it would be desirable to find a kind of scale (conformal)-invariance, because it is conjectured that cosmic string networks evolve scale-invariant just after the radiation dominated era of our universe. The intricate features of the po- larization axes alignments of the quasars in LQGs show at least a kind of co- evolution at very large scales [22] , so a study of conformal symmetry of our model could be of interest.
Gravity theory invariant under ![]() is local conformal invariant and must be spontaneously broken because our world appears not to be scale invariant [29] [30] . Let us rewrite our spacetime of Equation (1) with
is local conformal invariant and must be spontaneously broken because our world appears not to be scale invariant [29] [30] . Let us rewrite our spacetime of Equation (1) with ![]()
![]() (14)
(14)
where we renamed the warp factor as![]() . If we consider the
. If we consider the ![]() -dependent part of
-dependent part of ![]() and consider the flat (brane) case of the metric Equation (1),
and consider the flat (brane) case of the metric Equation (1),
![]() (15)
(15)
we then obtain for the Ricci scalar
![]() (16)
(16)
The Ricci scalar transforms under ![]() as [31]
as [31]
![]() (17)
(17)
So for conformal invariancy of![]() , the second term on the right hand side of Equation (17) must vanish. For
, the second term on the right hand side of Equation (17) must vanish. For ![]() we then find
we then find
![]() (18)
(18)
with constraint equations![]() . Equation (18) is just the equation of a vibrating circular drum. The general solution for the boundary conditions
. Equation (18) is just the equation of a vibrating circular drum. The general solution for the boundary conditions ![]() is
is
![]() (19)
(19)
with![]() ,
, ![]() Bessel functions and
Bessel functions and ![]() coefficients dependent of
coefficients dependent of![]() . These solutions represent for suitable boundary conditions, the standing normal modes of the brane in the vacuum case. In general,
. These solutions represent for suitable boundary conditions, the standing normal modes of the brane in the vacuum case. In general, ![]() can also depend on the azimuthal angle. This dependency is found, in our non-vacuum situation, in the preceding sections in the multiple-scale approximation. So one could conclude that the warp factor in the vacuum case fulfils a scalar wave equations re- presenting fluctuations of the brane in the ground state. It represents the amount of local “stretching” of the 4D geometry. In the non-vacuum case, with the U(1) scalar gauge field in the brane, one can try to formulate again the conformal invariance. This is a peculiar issue in theoretical physics till now. Einstein equations and the scalar equation (Klein-Gordon equation)) are not conformally invariant. One has to modify Einstein’s equations to make it conformally invariant and make the energy momentum tensor traceless [31] [32] . Our
can also depend on the azimuthal angle. This dependency is found, in our non-vacuum situation, in the preceding sections in the multiple-scale approximation. So one could conclude that the warp factor in the vacuum case fulfils a scalar wave equations re- presenting fluctuations of the brane in the ground state. It represents the amount of local “stretching” of the 4D geometry. In the non-vacuum case, with the U(1) scalar gauge field in the brane, one can try to formulate again the conformal invariance. This is a peculiar issue in theoretical physics till now. Einstein equations and the scalar equation (Klein-Gordon equation)) are not conformally invariant. One has to modify Einstein’s equations to make it conformally invariant and make the energy momentum tensor traceless [31] [32] . Our ![]() - field can play a crucial role in this context if one introduces an unavoidable dilaton field.
- field can play a crucial role in this context if one introduces an unavoidable dilaton field.
6. Conclusions
It is found on a five dimensional warped brane world spacetime, using a multiple-scale approximation scheme, that to second order the metric and scalar gauge field show a spectrum of azimuthal-angle dependent wavelike modes with extremal values dependent of the winding numbers of the background, first and second order perturbations of the scalar field.
In four dimensional models, this local field theory admits vortex-like behavior and is a generalization of the Ginzburg-Landau theory of superconductivity. A lattice of Abrikosov vortices can be formed, carrying a quantized flux dependent of the winding number or “vortex charge”![]() . Vortices with
. Vortices with ![]() are unlikely, since the energy is reduced if they split up into single vortices. However, in the general relativistic case, gravity comes into play and the energy of the con- figuration of the vortices must be calculated covariantly by means of the energy momentum tensor. This general relativistic vortex solution (cosmic string) can build up a huge mass per unit length in the bulk and can induce massive Kaluza-Klein modes felt on the brane, where the standard model fields reside. Disturbances don’t fade away during the expansion of the universe due to the warp factor.
are unlikely, since the energy is reduced if they split up into single vortices. However, in the general relativistic case, gravity comes into play and the energy of the con- figuration of the vortices must be calculated covariantly by means of the energy momentum tensor. This general relativistic vortex solution (cosmic string) can build up a huge mass per unit length in the bulk and can induce massive Kaluza-Klein modes felt on the brane, where the standard model fields reside. Disturbances don’t fade away during the expansion of the universe due to the warp factor.
There is a strong evidence of scaling (conformal) behaviour of long non- intercommuting cosmic strings networks during the radiation-dominated era. High or low initial string densities tend toward a fixed scaling value. However, standard cosmology, constraints such strings to be very light and will fade away (or disappear by the forming of closed loops). In our model they can survive by the warp factor. This fact makes the comparison with the alignment of quasars possible. So it would be desirable to have also a scale-invariant alignment structure. This is currently under study.
Appendix
A. The Background and First Order Perturbation Equations
In an earlier work [10] we obtained the equations for the background metric components (![]() ), background matter fields
), background matter fields ![]() and first order ap- proximation equations of
and first order ap- proximation equations of ![]() and
and![]() . They are
. They are
![]() (20)
(20)
![]() (21)
(21)
![]() (22)
(22)
![]() (23)
(23)
![]() (24)
(24)
![]() (25)
(25)
![]() (26)
(26)
![]() (27)
(27)
The background matter fields (![]() ) become [9]
) become [9]
![]() (28)
(28)
![]() (29)
(29)
and perturbation equations
![]() (30)
(30)
![]() (31)
(31)
![]() (32)
(32)
These background equations don’t contain perturbations terms, due to our (simplified) gauge conditions.
B. The Second Order Perturbation Equations
With the help of a algebraic manipulation program, we obtain from Equation (10), for example, the most interesting:
![]() (33)
(33)
and
![]() (34)
(34)
with ![]() a function of the background fields and the fields
a function of the background fields and the fields![]() . The other components of the metric perturbations are obtained in the same way. The second order equations for
. The other components of the metric perturbations are obtained in the same way. The second order equations for ![]() and
and ![]() are
are
![]() (35)
(35)
![]() (36)
(36)
There are the second order partial derivative terms ![]() and
and ![]() in Equation (35) and Equation (36) respectively. They can be isolated in order to get a wave equation for the first order perturbations.
in Equation (35) and Equation (36) respectively. They can be isolated in order to get a wave equation for the first order perturbations.
C. The Energy Momentum Components
For the several orders of the energy-momentum tensor components we find
![]() (37)
(37)
![]() (38)
(38)
![]() (39)
(39)
![]() (40)
(40)
![]() (41)
(41)
![]() (42)
(42)
![]() (43)
(43)
![]() (44)
(44)
![]() (45)
(45)
![]() (46)
(46)
![]()
Submit or recommend next manuscript to SCIRP and we will provide best service for you:
Accepting pre-submission inquiries through Email, Facebook, LinkedIn, Twitter, etc.
A wide selection of journals (inclusive of 9 subjects, more than 200 journals)
Providing 24-hour high-quality service
User-friendly online submission system
Fair and swift peer-review system
Efficient typesetting and proofreading procedure
Display of the result of downloads and visits, as well as the number of cited articles
Maximum dissemination of your research work
Submit your manuscript at: http://papersubmission.scirp.org/
Or contact jmp@scirp.org