Local Solutions to a Class of Parabolic System Related to the P-Laplacian ()
1. Introduction
The objective of this paper is to study the existence and uniqueness of local solutions to the initial and boundary value problem of the parabolic system
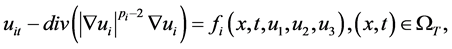 (1.1)
(1.1)
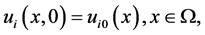 (1.2)
(1.2)
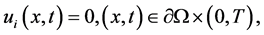 (1.3)
(1.3)
where 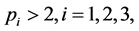
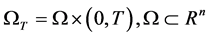 is a bounded domain with smooth boundary
is a bounded domain with smooth boundary . The conditions of
. The conditions of  and
and  will be given later.
will be given later.
System (1.1) is popular applied in non-Newtonian fluids [1] [2] and nonlinear filtration [3] , etc. In the non-Newtonian fluids theory, 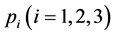 are all characteristic quantity of the medium. Media with
are all characteristic quantity of the medium. Media with 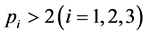 are called dilatant fluids and those with
are called dilatant fluids and those with 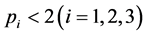 are called pseudoplastics. If
are called pseudoplastics. If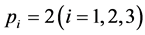 , they are Newtonian fluids.
, they are Newtonian fluids.
Some authors have studied the global finiteness of the solutions (see [4] [5] ) and blow-up properties of the solutions (see [6] ) with various boundary conditions to the systems of evolutionary Laplacian equations. Zhao [7] and Wei-Gao [8] studied the existence and blow-up property of the solutions to a single equation and the systems of two equations. We found that the method of [8] can be extended to the general systems of n equations. For the sake of simplicity, this paper only makes a detailed discussion on n = 3. Since the system is coupled with nonlinear terms, it is in general difficult to study the system. In this paper, we consider some special cases by stating some methods of regularization to construct a sequence of approximation solutions with the help of monotone iteration technique and obtain the existence of solutions to a regularized system of equations. Then we obtain the existence of solutions to the system (1.1)-(1.3) by a standard limiting process. Systems (1.1) degenerates when 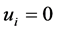 or
or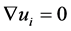 . In general, there would be no classical solutions and hence we have to study the generalized solutions to the problem (1.1)-(1.3).
. In general, there would be no classical solutions and hence we have to study the generalized solutions to the problem (1.1)-(1.3).
The definition of generalized solutions in this work is the following.
Definition 1.1. Function 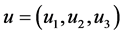 is called a generalized solution of the system (1.1)-(1.3) if
is called a generalized solution of the system (1.1)-(1.3) if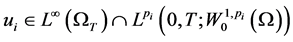 ,
, 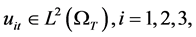 and satisfies
and satisfies
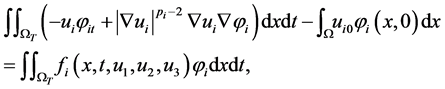 (1.4)
(1.4)
for any ![]() for
for ![]()
Equations (4) implies that
![]() (1.5)
(1.5)
The followings are the constrains to the nonlinear functions ![]() involved in this paper.
involved in this paper.
Definition 1.2. A function ![]() is said to be quasimonotone nondecreasing (resp., nonincreasing) if for fixed
is said to be quasimonotone nondecreasing (resp., nonincreasing) if for fixed![]() ,
, ![]() is nondecreasing (resp., non- increasing) in
is nondecreasing (resp., non- increasing) in ![]()
Our main existence result is following:
Theorem 1.3. If there exist nonnegative functions ![]() which are quasimonotonically nondecreasing for
which are quasimonotonically nondecreasing for![]() ,
, ![]() ,
, ![]() , and a non- negative function
, and a non- negative function ![]() such that
such that
![]() (1.6)
(1.6)
Then there exists a constant ![]() such that the system (1.1)-(1.3) has a solution
such that the system (1.1)-(1.3) has a solution ![]() in the sence of Definition 1.1 with
in the sence of Definition 1.1 with ![]() replaced by
replaced by![]() .
.
In Theorem 1.3, we just obtain the existence of local solution. As known to all, when the system degenerates into an equation, as long as some order of growth conditions is added on![]() , we can find the global solution, which is the main result of [7] . The existence of the global solution of (1.1)-(1.3) remains to be further studied.
, we can find the global solution, which is the main result of [7] . The existence of the global solution of (1.1)-(1.3) remains to be further studied.
On the other hand, similar to [8] , we made the assumption of monotonicity to![]() . From the current point of view, the condition is relatively strong. It is well worth studying how to reduce
. From the current point of view, the condition is relatively strong. It is well worth studying how to reduce ![]() monotonicity requirements of the system (1.1)-(1.3).
monotonicity requirements of the system (1.1)-(1.3).
2. Proof of Theorem 1.3
To prove the theorem, we consider the following regularized problem
![]() (2.1)
(2.1)
![]() (2.2)
(2.2)
![]() (2.3)
(2.3)
where![]() ,
, ![]() are quasimonotone nondecreasing and
are quasimonotone nondecreasing and ![]() uniformly on bounded subsets of
uniformly on bounded subsets of ![]() also
also
![]() (2.4)
(2.4)
![]() strongly in
strongly in![]() .
.
Lemma 2.1. The regularized problem (2.1)-(2.3) has a generalized solution.
Proof. Starting from a suitable initial iteration![]() , we construct a se- quence
, we construct a se- quence ![]() from the iteration process
from the iteration process
![]() (2.5)
(2.5)
![]() (2.6)
(2.6)
![]() (2.7)
(2.7)
where![]() . It is clear that for each
. It is clear that for each ![]() the above system consists of three nondegenerated and uncoupled initial boundary-value problems.
the above system consists of three nondegenerated and uncoupled initial boundary-value problems.
By classical results (see [9] ) for fixed ![]() and
and ![]() the problem (2.5)-(2.7) has a classical solution
the problem (2.5)-(2.7) has a classical solution ![]() if
if ![]() is smooth.
is smooth.
To ensure that this sequence converges to a solution of (2.1)-(2.3), it is necessary to choose a suitable initial iteration. The choice of this function depends on the type of quasimonotone property of![]() . In the following, we establish the monotone property of the sequence.
. In the following, we establish the monotone property of the sequence.
Set![]() . Let
. Let ![]() be a classical solution of the following problem.
be a classical solution of the following problem.
![]() (2.8)
(2.8)
![]() (2.9)
(2.9)
![]() (2.10)
(2.10)
By ![]() and the comparison theorem (see [10] ), we have that
and the comparison theorem (see [10] ), we have that
![]() (2.11)
(2.11)
Hence by the quasimonotone nondecreasing property of![]() , we have
, we have
![]() (2.12)
(2.12)
for![]() .
.
Using the same argument as above, we can obtain a classical solution ![]() of the problem
of the problem
![]() (2.13)
(2.13)
![]() (2.14)
(2.14)
![]() (2.15)
(2.15)
for![]() .
.
By the comparison theorem, we have
![]() (2.16)
(2.16)
By induction method, we obtain a nonincreasing sequence of smooth functions
![]() (2.17)
(2.17)
In a similar way, by setting ![]() we can get a solution
we can get a solution ![]() of
of
![]() (2.18)
(2.18)
![]() (2.19)
(2.19)
![]() (2.20)
(2.20)
with
![]() (2.21)
(2.21)
In the same way as above, we obtain a nondecreasing sequence of smooth functions
![]() (2.22)
(2.22)
It is obvious that![]() . By induction method, we may assume that
. By induction method, we may assume that![]() . Since
. Since ![]() is quasimonotone nondecreasing, we have
is quasimonotone nondecreasing, we have
![]() (2.23)
(2.23)
for![]() .
.
![]() (2.24)
(2.24)
![]() (2.25)
(2.25)
![]() (2.26)
(2.26)
![]() (2.27)
(2.27)
By the comparison principle, we have![]() . Therefore
. Therefore
![]() (2.28)
(2.28)
Taking![]() , we get a nondecreasing bounded sequence
, we get a nondecreasing bounded sequence
![]() . Hence there exist functions
. Hence there exist functions ![]() such that
such that
![]() (2.29)
(2.29)
By the continuity of ![]() we have
we have
![]() (2.30)
(2.30)
We now prove that there exist ![]() and a constant M (independent of k and
and a constant M (independent of k and![]() ) such that for all k, we have
) such that for all k, we have
![]() (2.31)
(2.31)
Let ![]() be the solutions of the ordinary differential equations
be the solutions of the ordinary differential equations
![]() (2.32)
(2.32)
By standard results in [11] , there exist![]() , such that
, such that ![]() exists on
exists on ![]() with
with ![]() depends only on
depends only on![]() . By the comparison theorem
. By the comparison theorem
![]() (2.33)
(2.33)
Setting![]() , we obtain (2.31).
, we obtain (2.31).
We now claim that ![]() as
as![]() , in
, in![]() , where
, where ![]() stands for weak convergence,
stands for weak convergence,![]() .
.
Multiplying (2.5) by ![]() and integrating over
and integrating over![]() , we obtain that
, we obtain that
![]() (2.34)
(2.34)
Furthermore
![]() (2.35)
(2.35)
![]() (2.36)
(2.36)
By (2.12) and the property of ![]()
![]() (2.37)
(2.37)
where C is a constant independent of ![]() and k.
and k.
Multiplying (2.5) by ![]() and integrating over
and integrating over![]() , we have
, we have
![]() (2.38)
(2.38)
By Cauchy inequality and integrating by parts, we obtain
![]() (2.39)
(2.39)
Hence
![]() (2.40)
(2.40)
By (2.37) and (2.40), we obtain that there exists a subsequence of ![]() converging weakly in the following sense as
converging weakly in the following sense as![]() .
.
![]() (2.41)
(2.41)
![]() (2.42)
(2.42)
![]() (2.43)
(2.43)
where ![]() stands for weak convergence,
stands for weak convergence,![]() .
.
From (2.29), (2.30), (2.37), (2.40) and the uniqueness of the weak limits, we have that, as![]() ,
,
![]() (2.44)
(2.44)
![]() (2.45)
(2.45)
![]() (2.46)
(2.46)
We now claim that ![]()
Multiplying (2.5) by ![]() and integrating over
and integrating over ![]() with
with ![]() we get
we get
![]() (2.47)
(2.47)
Hence
![]() (2.48)
(2.48)
Since the three terms on the right hand side of the above equality converge to 0 as![]() . This yields that
. This yields that
![]() (2.49)
(2.49)
On the other hand, since![]() , we have that
, we have that
![]() (2.50)
(2.50)
Note that
![]() (2.51)
(2.51)
Following (2.50) and (2.51), we have
![]() (2.52)
(2.52)
Since
![]() (2.53)
(2.53)
and
![]() (2.54)
(2.54)
by Hölder inequality, we have
![]() (2.55)
(2.55)
i.e.,
![]() (2.56)
(2.56)
Hence
![]() (2.57)
(2.57)
This proves that any weak convergence subsequence of ![]() will have
will have ![]() as its weak limit and hence by a standard argument, we have that as
as its weak limit and hence by a standard argument, we have that as![]() ,
,
![]() (2.58)
(2.58)
Combining the above results, we have proved that ![]() is a generalized solution of (2.1)-(2.3).
is a generalized solution of (2.1)-(2.3).
Proof of theorem 1.3.
Since ![]() satisfy similar estimates as (2.31), (2.37) and (2.40), combining the property of
satisfy similar estimates as (2.31), (2.37) and (2.40), combining the property of![]() , we know that there are functions
, we know that there are functions ![]() (as
(as![]() ) such that for some subsequence of
) such that for some subsequence of ![]() denoted again by
denoted again by![]() ,
,
![]() (2.59)
(2.59)
![]() (2.60)
(2.60)
![]() (2.61)
(2.61)
![]() (2.62)
(2.62)
In a similar way as above, we prove that ![]()
By a standard limiting process, we obtain that ![]() satisfies the initial and boundary value conditions and the integrating expression. Thus
satisfies the initial and boundary value conditions and the integrating expression. Thus ![]() is a generalized solution of (1.1)-(1.3).
is a generalized solution of (1.1)-(1.3).
3. Uniqueness Result to the Solution of the System
We now prove the uniqueness result to the solution of the system.
Theorem 3.1. Assume ![]() is Lipschitz continuous in
is Lipschitz continuous in![]() , then the solution of (1.1)-(1.3) is unique.
, then the solution of (1.1)-(1.3) is unique.
Proof. Assume that ![]() and
and ![]() are two solutions of (1.1)- (1.3). Let
are two solutions of (1.1)- (1.3). Let ![]() then following (1.5),
then following (1.5),
![]() (3.1)
(3.1)
![]() (3.2)
(3.2)
By (3.1) subtracting (3.2), we get
![]() (3.3)
(3.3)
By the inequality (3.3) and the Lipschitz condition, a simple calculation shows that
![]() (3.4)
(3.4)
Setting![]() , then (3.4) can be written as
, then (3.4) can be written as![]() . Since
. Since![]() , by a standard argument, we have
, by a standard argument, we have![]() , and hence
, and hence![]() .
.