Design Optimization of Axial Flux Permanent Magnet (AFPM) Synchronous Machine Using 3D FEM Analysis ()
1. Introduction
Over the last decades, the increasing interest in the study of axial flux permanent magnet synchronous machines (AFPMSM) has led to a variety of designs and applications for this type of machines. Their uses as generators in small-scale wind turbines, in electrical vehicles and in robotics are some of their usual applications [1] [2] . Some of their main characteristics are the simplicity of construction, as well as the ability to install a large number of poles. The latter feature gives them a distinct advantage, as it eliminates the need for a gearbox, thus making the application cost effective and more reliable [3] . Despite the number of publications already available in international bibliography, there still exist areas for further study and development on this topic. This paper contributes in this ongoing research.
With the current availability of high energy magnets, the stators of AFPM brushless machines can be fabricated without cores. Specifically, a coreless design reduces the mass while increasing the efficiency of the machine [4] . In addition, there is no production of any attractive force between the stator and the rotor, nor any torque pulsations at zero current state, meaning no cogging (detent) torque. To overcome the limitations in torque when using a single rotor, a multi disk topology is preferred.
Contributions regarding AFPMSM with iron cores can be found in the literature dealing mainly with the effect of magnet shape on the quality of the electromagnetic torque and the cogging torque reduction [5] [6] . On the other hand, the research on the optimization procedures in AFPMSMs with double external rotors and a coreless internal stator is limited [7] .
The machine used in this study consists of a twin rotor with neodymium-iron-boron NdFeB magnets and the coreless stator winding, embedded in resin, located between the two rotors [4] [8] . The purpose of this study is firstly to examine the behavior of the AFPM machine under four different magnet topologies. To accomplish this, the four machine models were simulated and compared under open loop, as well as, under load condition for a variety of loads. Furthermore, the optimum model, under certain criteria, was selected in order to study the influence of the rotor material on the magnetic field and the machine behavior, more specifically on the output power, torque ripple and the power factor.
The complexity of the machine’s geometry is such that does not allow accurate solution through analytical equations. The finite element method (FEM) was used instead, where the model body can easily be analyzed in several discrete finite elements for which the Maxwell equations can be applied. For this particular model geometry, the nonlinear 3D FEM analysis was selected and achieved using a solver which can be used to compute electromagnetic fields including the effects of eddy currents in moving systems in three dimensions, of the Cobham Opera software [9] .
2. AFPM Machine Models
2.1. Machine Variables
The under investigation machine (3-phase generator with two rotors and one inner stator) whose parameters are chosen according to the good and safe operation of the machine [4] [10] are presented in Table 1. Table 2 includes the calculated variables from the analytical equations that describe this type of machine [4] [11] [12] .
The σr parameter expresses the ratio between inner to outer radius of the active part of the stator winding. The optimum value is σr = 0.577 [4] and therefore the selected value for the present machine is chosen 0.48, close to the optimum.
According to the parameters above, the following four Axial Flux Permanent Magnet (AFPM) machine models were designed in 3D while preserving all properties and dimensions (rotor width, B-H curves, stator coils) except the magnet shape. The material for the two rotors is steel and each one has sixteen permanent magnets (neodymium- iron-boron NdFeB) mounted evenly on the surface.
![]()
Table 2. Calculated variables from the theoretical equations.
The stator is coreless and it consists of twelve concentrated, non overlapping, trapezoidal coils immersed in a resin type material with air characteristics. There is a variety of non overlapping coil topologies such as trapezoidal, rhomboidal, hexagonal and circular coils. Trapezoidal coils can achieve the best use of the magnetic field, however due to their large non active areas, this results in more copper losses. Rhomboidal coils do not have non active areas and copper losses are minimized, but this characteristic has the disadvantage to exploit less magnetic field than the trapezoidal coils. Hexagonal shape is a combination of the previous two coil types which can have significant difficulties in construction process. Finally, circular coils are not preferable due to their limited active part [8] . For the purpose of this study, the trapezoidal coil type was selected.
Considering the Finite Element Analysis (FEA) models, proper mesh size must be used at the different parts of the machine regarding the accuracy of the computation results. The most dense mesh design is needed for the air-gap area. The number of the surface elements is ~65000, the volume elements ~275000 and the required time for one time-step iteration is ~5 min with Intel Core i5-3570K CPU @ 3.5 GHz, 16 GB RAM and 64-bit operating system.
2.2. Simulation Models
As previously stated, the impact of magnet design in the machine performance is under investigation. The categorization of the magnets depends on their shape, hence their label categorization as radial, conventional skew, dual skew and finally triangular skew magnets [12] . Figure 1 is presenting the corresponding designs used in the simulations. In each model the number and the radial length of the magnets is the same, but the volume of the magnetic material is different, due to the different designs. In Table 3 the magnet surface area of the chosen topologies is presented.
In order for the simulation results to be comparable, all model dimensions and test conditions apart from the magnets shape were kept unaltered. The magnets used in the simulation are NdFeB, grade Ν42.
![]()
Figure 1. (a) Radial magnets, (b) Conventional skew magnets, (c) Dual skew magnets, (d) Triangular skew magnets.
![]()
Table 3. Magnet surface area for the different models.
3. Simulations Results
All four 3D FEM models were simulated in open loop condition as well as under load of 60 Ω/phase in star (Y) formation. All simulations were performed for the nominal speed of 375 rpm. The nonlinear 3D FEM analysis was selected and achieved using a solver which can be used to compute electromagnetic fields, including the effects of eddy currents, in moving systems in three dimensions.
3.1. Axial Field Representation
Due to the shape of the magnets, each model displays a different magnetic field, with different magnitude and space distribution. This can be observed in Figure 2. This in turn will affect the machine operational parameters, as it will be shown in the following sections.
3.2. Open-Loop Condition
Using the same OPERA 3D solver, which takes into account the rotor revolution, several time-varying electromagnetic variables were extracted. The nominal speed of 375 rpm was once again applied in the open-loop condition. It was also performed a reversed revolution simulation of equal rotational speed, because of the asymmetric geometry of the conventional and dual skew magnet models. Figure 3 shows the steady state phase voltage waveforms in open-loop condition. The rms voltage values of each model are presented in Table 4.
The dual skew model produces the maximum voltage, followed by the triangular skew model. As regard to the reversed revolution simulations, the results indicate that
![]()
Figure 2. Magnetic flux distribution in the mid airgap for the four different AFPM models (a) Radial magnet model, (b) Conventional skew magnet model, (c) Dual skew magnet model, (d) Triangular skew magnet model.
![]()
Figure 3. Steady state phase voltage waveforms in open-loop condition.
![]()
Table 4. Open loop voltage rms values.
there is small difference in voltage output values in comparison with the normal rotating models. Specifically, conventional skew and its reversed model have a 0.7% difference and dual skew and its reversed model have a 0.9% difference. Consequently, conventional and dual skew magnet topologies can be used for both directions of rotation without having significant variation in output values.
3.3. Simulation under Load
While preserving the nominal rotational speed at 375 rpm, a three-phase star connected (Y) load of 60 Ω/phase was connected.
As expected, each model produces different voltage output and torque waveforms depending on the magnet topology. In Table 5, the results in regard with the mechanical input power, the electrical output power, the generated torque and the rms values of voltage and current are presented accordingly for each model. Finally, the last column contains the power factor. The models that show the best performance regarding the output power and torque, are Dual and Triangular skew followed by Radial and Conventional skew magnet models.
In Figure 4 it is presented the phase voltage and the power factor versus load for the various models. As expected, the above performance conclusions stand also for operation under various loads.
The torque waveforms are presented in Figure 5.
Although most published studies refer to similar AFPM topologies, their main focus is the minimization of cogging torque. Despite the lack of stator cores in this type of generator, meaning no cogging torque and less stator weight, there is still interest in studying how these magnet designs affect the torque waveform [13] [14] [15] .
![]()
Table 5. Output generator values under 60 Ω/phase load and 375 rpm.
![]() (a)
(a)![]() (b)
(b)
Figure 4. Plot versus the load of: (a) the phase voltage and (b) the power factor, for the various models.
![]()
Figure 5. Waveforms of torque vs time for each model.
Torque ripple-induced vibration can be amplified because of other mechanical system parts, creating acoustic noise. The effects of torque ripple are unpleasant in more challenging motion control and machine-tool applications because of speed fluctuations that degrade the performance [16] . In addition, torque ripple may excite resonances in the mechanical portion of the drive system producing acoustic noise especially in machine-tool applications, where it leaves visible patterns in high-precision machined surfaces.
As known, the amplitude of torque ripple increases at low speeds. In addition, the effect of the moment of inertia that tends to absorb shaft speed variations, is less significant at lower rate of speed fluctuations. A smooth air-gap torque is particularly desired at low speed [17] .
To achieve the comparison between torque ripple pulsation of the simulated models, the mean square error equation is used. This allows the calculation of the deviation between the waveform of torque ripple of each model and the reference waveform of torque. As reference waveform of torque a straight line, time-invariant and equal to the mean value of each topology, is used.
As the MSE (mean square error) result tends to zero, the torque ripple error diminishes, resulting to values that approach the mean torque value. In comparison, the further the MSE value is distanced from zero, the greater the error and so the torque waveform ripple from the average value [18] [19] . The mean square error is calculated using the Equation (1):
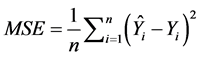 (1)
(1)
where:
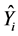 : Average value of torque
: Average value of torque
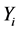 : The value of the torque per iteration
: The value of the torque per iteration
The calculated results are shown in Table 6.
![]()
Table 6. Torque ripple MSE (%) for each Magnet topology.
Considering this study is intended for the construction of a small scale application, the main desire is to obtain maximum torque and output power for low speed usages, while maintaining the construction lighter (no extra weight from stator cores) and at a minimum level of complexity.
The under investigation simulation models were compared for the same load and revolution speed. Summarizing the already established results, the models that show the best performance regarding the output power and torque, are Dual and Triangular skew magnet models. On the other hand, comparing the torque oscillations the best models are the Radial and Dual skew magnet models. However, as the simplicity and the cost of production must be taken under consideration too, the model selected for further investigation was the Triangular skew magnet topology, as shown in Figure 6.
4. Rotor Material Investigation
The selected model with triangular magnets was further simulated for several rotor disk materials. As the magnetic flux orientation of the used magnets is axial, it is necessary that the rotor material presents ferromagnetic characteristics as to assist and amplify the direction and density of the magnetic flux. Therefore, six different types of steel, commercially available, were selected to be tested.
Steel, is actually a lab sample of extremely soft iron with almost no impurities, created for our solver software by Thyssen, as an all purposed steel [9] .
Stainless steel 304 is the most common stainless steel. It is not very electrically or thermally conductive and is non magnetic. It has a higher corrosion resistance than regular steel and is widely used because of the ease in which it is formed into various shapes. Also it has excellent resistance to a wide range of atmospheric environments and many corrosive media. Stainless steel 304 is used for a variety of household and industrial applications such as screws, machinery parts, car headers etc [20] [21] .
Stainless Steel (SS) 416 is a martensitic free machining grade of stainless that can be hardened by heat treatment to achieve elevated strength and hardness. Due to its low cost and ready machinability, stainless steel 416 is readily used in its highly tempered state. It exhibits better machining characteristics than austenitic grades, however, sacrifices corrosion resistance. High sulfur, free-machining grades like Alloy 416 are unsuitable for marine or any chloride exposure situations. Stainless steel 416 can be supplied for any project big or small [22] [23] .
![]()
Figure 6. Chosen topology for further investigation.
Silicon steels, are used for electrical transformer cores and cores of other electrical devices for the following reasons: a) low hysteresis loss, b) high permeability, c) high resistance and d) virtually eliminated ageing. However, the primary reason is the low hysteresis loss caused due to the impeding action of silicon atoms in the path of eddy currents [24] [25] .
Electrical steel M19, also called lamination steel, is specialty steel tailored to produce certain magnetic properties, such as a small hysteresis area (small energy dissipation per cycle, or low core loss) and high permeability. The material is usually manufactured in the form of cold-rolled strips less than 2 mm thick. These strips are called laminations when stacked together to form a core. Once assembled, they form the laminated cores of transformers or the stator and rotor parts of electric motors [24] [25] .
Plain carbon-mild steel is a metal alloy and it is a combination of two elements, iron and carbon. Mild steel is the most common form of steel as its price is relatively low while it provides material properties that are acceptable for many applications. Mild steel has a low carbon content (up to 0.3%) and is therefore neither extremely brittle nor ductile. It becomes malleable when heated, and so can be forged. It is also often used where large amounts of steel need to be formed, for example as structural steel [26] [27] .
In Figure 7 the B-H curves of the aforementioned steel types are demonstrated.
The under investigation models, with different rotor material, were simulated. The calculated axial magnetic flux density in a radial length of 90.5 mm, along the z axis is presented in Figure 8.
The axial width of the model is approximately 50 mm. The magnetic flux must be confined in the limits of the axial width. The ferromagnetic properties of the various steel types, used in the rotor disks, provide a path through which the magnetic flux is maintained within the rotor disks. The variety of relative magnetic permeability (μr) of the materials in the linear region and also the effect of the B-H curves on the output open loop voltage are presented in Table 7.
All steel types, despite their different physical and magnetic properties and chemical composition, seem to have similar effect on the back EMF, with the only exception of
![]()
Figure 7. B-H curves of different steel types.
![]()
Figure 8. Magnetic flux in z direction, in radial length of 90.5 mm along the z axis.
![]()
Table 7. Relative magnetic permeability of materials in linear region and open loop rms phase voltage for different rotor disks materials.
the stainless steel 304 that presents significantly lower output voltage. The later happens because this type of material demonstrates properties similar to air (μr ≈ 1) [21] .
As shown in Figure 7 and Table 7 the B-H magnetic curves of the proposed materials present significant deviation. For the purpose of further investigation, an additional electromagnetic analysis was conducted in order to study and compare the behavior of the machine for two types of back-iron material. The selected types of steel are the steel (soft iron), which was used in section 3.2 and the mild steel, due to their obvious divergence. Their main differences lie in the value of relative magnetic permeability (μr) as well as in the fact that the mild steel saturation knee is approximately at 0.7 T, while the steel saturation knee is at 1.3 T. Because of the aforementioned attributes, the two models were simulated under various loads and the same rotational speed. The results are presented in Table 8.
As seen from Table 8 the machines with two different rotor materials present almost the same behavior, except for load values around 60 Ω, where the machine with the steel rotor discs performs slightly better. The final selection of the material of the rotor depends on the nature of the application, the availability of steel, the installation site, the corrosion factor and the construction cost.
5. Conclusion
The purpose of this paper was to investigate the behavior of a low speed axial flux permanent magnet synchronous generator for small power applications, providing options considering the operational behavior, the desirable construction complexity, the availability of material and the cost. Firstly, the chosen parameters of the AFPM machine were indicated, as well as, the calculated variables from the analytical equations. Using nonlinear 3D FEM electromagnetic analysis, the selected AFPM models preserving all properties and dimensions except the magnet shape were simulated. Performance results under both open loop and load were extracted. The simulation results were compared and a further investigation in torque ripple for each model was performed. The
![]()
Table 8. Comparison of performance behavior of steel and mild steel, as rotor material, under various loads and the same rotational speed.
triangular skew magnets model was chosen because of its high output power, power factor, low cost and the simplicity of production. A more extensive analysis was performed regarding the rotor disk material on the selected model. Finally, the simulations have shown how the different types of commercially available steel affect the magnetic field and the performance of the machine.
Acknowledgements
This work was supported by the Laboratory of Electromechanical Energy Conversion of Electrical and Computer Engineering Department in the University of Patras, Greece and its members.