Cubic Spline Regression: An Application to Early Bipolar Disorder Dynamics ()
1. Introduction
Spline is a numeric function that is piecewise-defined by polynomial functions and which possesses a high degree of smoothness at the places where the polynomial pieces connect (which are known as knots) Chen 2009 [1] , Judd 1998 [2] . As noted by Harrell et al. (1988) [3] , splines are smooth functions that can assume virtually any shape, and the most useful type of spline is generally a cubic spline function, which is restricted to be smooth at the junction of each cubic polynomial. A restricted cubic spline model has been used in epidemiological studies and it is often applied to nonlinear dose-response data as noted by Larsson and Orsini (2011) [4] . Takahashi et al. (2013) [5] applied a restricted cubic spline with three knots recently to a potential nonlinear association that was depicted as a J-shaped curve based on the likelihood-based assignment of values to grouped intervals of exposure. The most commonly used spline is the cubic spline functions. Spline regression has been widely used in different spheres.
Berberoglu and Berberoglu (2011) [6] applied cubic spline regression to model the structural shifts in exchange rate in Turkey from 1987-2008. Cubic spline regression was used to expose structural changes which resulted because of the economic policies. They built different cubic spline regression and picked the most significant of the models. In their study, cubic spline models was also identified as the most powerful and important weapon on the existence of structural shifts or changes in time series. They also pointed out how predicted sum of squares statistics residual can improve the analysis in cubic spline models. The usefulness of spline regression cannot be over emphazied because it represents a less biased and more efficient alternative to standard linear, curvilinear, or categorical analyses of continuous exposures and confounders in observational study [7] . Benefits of restricted cubic and quadratic splines have been described in the epidemiological and biomedical literature ( [3] and [8] ).
In order to draw our attention to some of the challenging issues to health, this paper thus addresses the two major problems of the MDQ which are
・ The problem of which rule is the best to decide bipolar risk tendency.
・ The problem of response bias from patients most especially when the patient’s statement is incoherent or contradicts that of the care giver.
The paper use the cubic spline curve to explore the bipolar disorder dynamics in relation to the behaviour of MDQ scores across the false negative and false positive knots and also estimate the real MDQ score for patient suspected of incoherent statements.
The importance of Mood Disorder Questionnaire (MDQ) developed by a committee of mental health experts in predicting the risk of bipolar disorder has been a course of concern for psychiatrist and researchers in mental health. The present rule of deciding bipolar risk is based on patients’ response during clerking; meeting some diagnostic criteria (Hirschfeld et al. 2000 [9] ). This is obviously subject to response bias as many patients may resort to lying just to avoid admission or avoid been stigmatized.
2. Methodology
Let the function
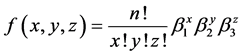(1)
be the trinomial distribution (a special case of the multinomial distribution); where x and y are non-negative integers with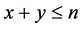 
and
. Also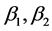
and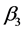
are the positive proper fraction with constrains 
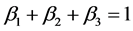and let 
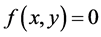elsewhere (Hogg and Craig [10] ), (Mood et al. [11] ).
The natural log-likelihood function of (1) for kth trials is given as
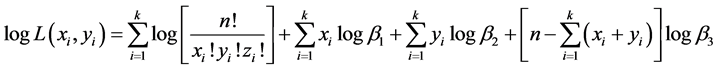(2)
Note that n is fixed and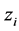 
is a random variable given as 
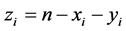which in reality is a partition beyond the space of
.
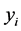Expressing (2) as a family of exponential class joint probability density function, then we have
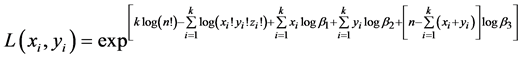(3)
Comparing (3) to the general form of the exponential class
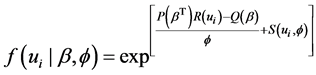we observed that the natural parameter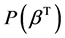 
is the vector of the model parameters
; the sufficient statistics
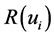is the vector of the model matrix
; the base measure is
, the log-partition function is ![]()
while the scale parameter is ![]()
= 1 (Hogg and Craig [9] , p. 231).
Hence the monotone and differentiable link functional relationship (g) between the expected response value of the random component ![]()
and the systematic (linear predictor) component is
![]()
(4)
Supposing![]()
, ![]()
and ![]()
are partitions according to the earlier assumptions of the committee of mental health experts (Hirschfeld et al. 2000 [9] ); then (4) is a piece-wise linear mixture of probability density for kth trials where each trial is partitioned into three groups of distinct intervals.
So extending the linear function representation in (4) to its cubic polynomial form, we have
![]()
(5).
Hence Equation (5) is the cubic polynomial spline equation for the kth trials trinomial model over the boundary conditions
![]()
(6)
To estimate the parameters, we maximized (5) by differentiating piece-wisely with respect to the parameters. The resulting homogeneous matrix ![]()
is then solved via characteristic function ![]()
for the eigen-values ![]()
and linear function ![]()
for the eigen vectors ![]()
(See Johnson and Wichern (2007) [12] ). A is the square of the rectangular matrices in (5).
3. Application
A total of seven hundred students that filled the mood disorder questionnaire and agreed to have landed in at least minor problems as a result of their irrational behaviour over a period of three months were used in the study. None of the respondents has reported in any psychiatric facility before. The observed scores were then simulated to a sample size of ![]()
each for the three different category of bipolar risk. Note that the scores are discrete. That is the number of yes score in a single trial (a single mood disorder questionnaire filled) is partitioned into three groups which are Bipolar NOS (Bipolar Not Otherwise Specified)![]()
, Bipolar I![]()
, and Bipolar II![]()
. The maximum number of yes scores in a single trial is fixed ![]()
(Hirschfeld et al. 2000 [9] ).
4. Result
Cubic spline equation for each of the mood disorder grouping.
Bipolar NOS: Bipolar Not Otherwise Specified.
5. Discussion of Result
Figure 1, reveals two maximum points (Knot 3 and Knot 7) and two minimum points (Knot 4 and Knot 8) indicating three separate density groups. The intermediate group is at knot 4 and knot 8, with false negative interval between knot 4 and knot 5 and false positive interval between knot 6 and knot 7. Any patient with a score of knot 3 belongs to the Bipolar NOS group. The Bipolar II group begins at knot (4). So there is uncertainty of classification between knot 3 and knot 4 and likewise between knot 7 and knot 8. So Bipolar I begin from Knot 8.
Figure 2 is useful to remove the problem of patients’ bias. Any incoherent patient with a claim of MDQ score 2 can be adjusted for bias via the graph in Figure 2. From the graph, the patient’s real estimated score in Bipolar II group is between 5 and is tending towards 8; while its score in the Bipolar I group is within the interval 8 - 9. This will guide the psychiatrist on the best therapy to give to the patient despite his/her incoherent claim.
![]()
Figure 1. The general bipolar mood disorder dynamics.
![]()
Figure 2. Combined curve of the general and the individual bipolar mood disorder dynamics.
Figure 3 is the plot of continuous scores for the MDQ as against the initial assumption of discrete scores as agreed by the experts that developed the questionnaire. The plot revealed that Bipolar NOS group is truly before the knot 4. While knot 4 marks the beginning of classifying bipolar patient to the Bipolar II group. However, the fluctuation in the bipolar disorder risk tendency is well captured in Figure 3 as against what we have in Figure 2. The bipolar disorder relative risk tendency is approximately 0.22 at knot 5, this dropped to 0.158 at knot 6 (a drop of about 28.2%). This implies that despite the increment in the mood disorder score, the bipolar disorder relative risk tendency is not directly increasing. Also, a more pronounced drop occurs between knot 9 and knot 10 (0.378 to 0.08 respectively representing a drop of about 78.8%).
![]()
Figure 3. Bipolar disorder dynamics assuming continuous score for MDQ.
6. Conclusion and Recommendation
The fluctuation in the dynamics of bipolar disorder at different knots is responsible for the unnoticed prolonged build up of bipolar disorder in the body. So this study recommends that any patient that has a MDQ score of at least 4 is a potential bipolar patient and should be treated accordingly given the necessary therapy. This is because bipolar disorder risk tendency begins to build up unnoticed from knot 4. Anyone with MDQ score of three below should be monitored appropriately until the level of mood disorder can be specified. We also recommend Figure 2 in addressing incoherent claim in patients’ submission. Finally we recommend proper awareness of mood control among individuals without psychiatric history majorly within students in tertiary institution.
Appendix (R 3.22)
Appendix: THE PROGRAM TO CONSTRUCT THE SPLINE CURVE
> a<-c(1,2,3)
> b<-c(4,5,6,7)
> c<-c(8,9,10,11,12,13)
> h<-array (a, dim=c(1,1416))
>I <-array (b, dim=c(1,1416))
> j<-array(c, dim=c(1,1416))
> s1<-0.9566+0.60366*h+2.110223*(h^2)+1.5384492*(h^3)
> s2<-0.9804259+0.709728*(i-3)+2.199303*((i-3)^2)+1.66667*((i-3)^3)
> s3<-0.9935901+0.8356599*(j-7)+2.4060235*((j-7)^2)+1.5584908*((j-7)^3)
> d<-c(h,i,j)
> s4<-c(s1,s2,s3)
>plot(d,s4)
> g <- plot(d,s4)
> lines(spline(h, s1, n = 1416, method = "natural"), col = 3)
> lines(spline(i, s2, n = 1416, method = "natural"), col = 2)
> lines(spline(j, s3, n = 1416, method = "natural"), col = 3)
> lines(spline(d, s4, n = 1416, method = "natural"), col = 4)