Enhancement in Channel Equalization Using Particle Swarm Optimization Techniques ()
1. Introduction
Channel equalization [1] [2] plays a pivotal role in high speed digital transmissions to recover the effect of inter symbol interference (ISI). An adaptive equalizer is positioned at the front end of the receiver to automatically adapt the time-varying nature of the communication channel. Adaptive algorithms are utilized in equalization to find the optimum coefficients. The normal gradient based adaptive algorithms such as Least Mean Square (LMS), Recursive least squares (RLS), Affine Projection algorithm (APA) and their variants [1] [2] [3] [4] applied in channel equalization converge to local minima [5] [6] [7] while optimizing the filter tap weights. The derivative free algorithms find the global minima by passing through local and global search processes. PSO is one of the derivative free optimization algorithms which search the minima locally and globally.
PSO is proven as an efficient method to update the weights of equalizer in adaptive Equalization [6] . PSO becomes one of the best algorithms for channel equalization in the recent years [6] [7] . While comparing to genetic algorithm, PSO needs minimum iterations to converge to minimum mean square error (MSE) in channel equalization [1] . To find the best optimum weights of equalizer, PSO updates the weights in each iteration using global best value and local best value [1] . The general equation [8] [9] used to update the weights in each iteration is,
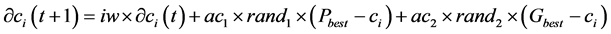 (1)
(1)
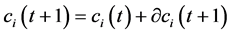 (2)
(2)
The positive constants 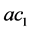 and
and 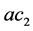 are called as cognitive and social acceleration coefficients.
are called as cognitive and social acceleration coefficients. 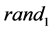 and
and 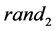 are two random functions in the interval [0,1].
are two random functions in the interval [0,1]. 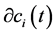 and
and 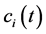 are velocity and position of particle i respectively in tth iteration.
are velocity and position of particle i respectively in tth iteration.
At each iteration, the change in weights are calculated by Equation (1) and the weights are modified to new one using Equation (2). Initially, the weights are randomly selected from the search space for P number of particles. Using the randomly selected weights, the fitness function is calculated and based on it, 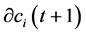 is updated and forwarded for next iterations.
is updated and forwarded for next iterations.
The PSO algorithm can be improved by modifying its inertia weight parameter and other parameters. Inertia weight parameter was initially introduced by Shi and Eberhart in [10] . Some of the time varying inertia weight modified methods are listed in Table 1.
2. Model and Methodology
Figure 1 depicts a basic block diagram used in adaptive equalization [1] . The input is the random bipolar sequence {x(n)} = ±1 and channel impulse response is raised cosine
![]()
Table 1. Time varying inertia weight modifications.
![]()
Figure 1. Block diagram of digital communication system.
pulse. The channel output is added with the random additive white Gaussian noise (AWGN). The noise sequence has zero-mean and variance 0.001.
The raised cosine channel response is represented as
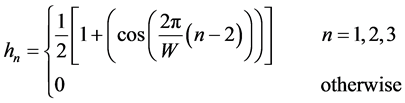 (3)
(3)
The factor W controls the amount of distortion. The effect of nonlinearities generated by the transmitter is modeled as three different nonlinear equations in (4), (5) and (6).
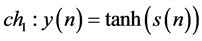 (4)
(4)
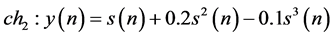 (5)
(5)
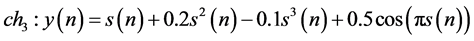 (6)
(6)
where 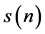 is the convolution of input
is the convolution of input 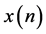 and channel impulse response
and channel impulse response 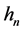 (i.e.)
(i.e.)![]() . The input to the receiver is
. The input to the receiver is
![]() (7)
(7)
where ![]() is the distorted version of the input signal.
is the distorted version of the input signal. ![]() is the noise component modeled as white Gaussian noise with variance
is the noise component modeled as white Gaussian noise with variance![]() . The noise added signal
. The noise added signal ![]() is given as input to equalizer.
is given as input to equalizer.
The error e(n) can be calculated as
![]()
where d(n) is the desired or training data. The adaptive algorithm updates the equalizer weights iteratively to minimize e2(n). Since e2(n) is always positive and gives the instantaneous power, it is selected as cost (fitness) function.
System Model
The system models [1] used for equalizer are simple linear transversal (tapped-delay- line) equalizer and decision feedback equalizer as shown in Figure 2 and Figure 3. In LTE structure the present and old values ![]() of the received signal are weighted by equalizer coefficients (tap weights) cq and summed to produce the output. The weights are trained to optimum value using adaptive algorithm. The output Zk becomes
of the received signal are weighted by equalizer coefficients (tap weights) cq and summed to produce the output. The weights are trained to optimum value using adaptive algorithm. The output Zk becomes
![]() (8)
(8)
DFE is a nonlinear equalizer usually adopted for channels with severe amplitude distortion. The sum of the outputs of the forward and feedback part is the output of the equalizer. Decisions made on the forward part are sent back via the second transversal filter. The ISI is cancelled by deducting past symbol values from the equalizer output. The output of DFE is calculated as
![]()
Figure 2. Linear transversal equalizer structure.
![]()
Figure 3. Decision feedback equalizer structure.
![]() (9)
(9)
3. Training by PSO
3.1. Basic PSO
The PSO based equalizer [6] optimizes the tap weights based on the following steps:
For LTE:
・ Error is estimated by comparing delayed version of each input sample with equalizer output
・ The mean square error function of each particle P is
![]()
・ Fitness value MSE(P) is minimized using PSO based optimization.
・ If the MSE of a particle is less than its previous value, term it as current local best value and its corresponding weight values as Pbest.
・ The minimum of MSE of all particles in every iteration is taken as global best value.
・ If the current global best value is better than the previous one, assign the corresponding tap weights to Gbest.
・ Calculated the change in position (Tap weights) of each particle using Equation (1).
・ Moved each particle (Tap weights) cq in Equation (8) to new position by Equation (2).
・ Repeated the above steps for the number of iterations specified or stopped when the algorithm converges to an optimum value with least MSE value.
For DFE:
・ The coefficients are initialized randomly for forward and feedback filter.
・ In the first iteration, only forward filter is active and after calculating the error the output of the forward filter is feedback through feedback filter.
・ The output of equalizer is calculated by subtracting the output of forward and feedback filters.
・ The forward and feedback filter coefficients cq and bi in Equation (9) are updated based on Equations (1) and (2).
3.2. Proposed Strategies
In most of the PSO variants the inertia value usually varies from high (1) to low (0). Initial search or global search requires high inertia value for particles to move freely in the search space. When inertia value gradually shifts to low, the search shifts from global to local to minimize MSE. The sudden shift of inertia weight from high to low after some initial steps minimizes the MSE better than gradual change of inertia value. The proposed algorithm uses a control function which suddenly shifts the inertia weight from high to low after a particular iteration as in Equations (10)-(12) and also shown in Figure 4.
![]() (10)
(10)
![]() (11)
(11)
![]() (12)
(12)
The common factor used in all time varying inertia weight algorithms is![]() , where m denotes maximum iteration and n denotes current iteration. This factor η changes linearly from 1 to 0. If Equation (10) is modified with a decreasing control function, it gives an effective time varying inertia weight strategy as shown in Equations (11) and (12). The term N in Equations (11) and (12) is the intermediate iteration value used to reduce the value of inertia weight suddenly after Nth iteration. This reduction produces optimum performance compared to existing inertia weight modified methods in terms of convergence speed and MSE.
, where m denotes maximum iteration and n denotes current iteration. This factor η changes linearly from 1 to 0. If Equation (10) is modified with a decreasing control function, it gives an effective time varying inertia weight strategy as shown in Equations (11) and (12). The term N in Equations (11) and (12) is the intermediate iteration value used to reduce the value of inertia weight suddenly after Nth iteration. This reduction produces optimum performance compared to existing inertia weight modified methods in terms of convergence speed and MSE.
In second modification, the position update ![]() in Equation (2) is updated by adding the change in position with its local best weight value. In all PSO variants the position is updated by adding change in position with previous iteration weights. If the previous iteration weights are replaced with its particle personal best value, it improves
in Equation (2) is updated by adding the change in position with its local best weight value. In all PSO variants the position is updated by adding change in position with previous iteration weights. If the previous iteration weights are replaced with its particle personal best value, it improves
![]()
Figure 4. Proposed inertia weight strategies.
the convergence speed more than 20 iterations and is proved in simulation results.
![]() (13)
(13)
where Pbest is the local best value of particle i till tth iteration. Since the local best weight is the best of all weights till that iteration for the corresponding particle, it automatically speeds up the convergence. The global best in Equation (1) includes the global search in each iteration to avoid local minima.
4. Simulation Results
4.1. Convergence Analysis
The general parameters assigned for simulations are specified in Table 2. The simulations are performed in MATLAB R2008b version. The simulations are observed for average of 10 independent runs. The proposed techniques, PSO with time varying inertia weights PSO-TVW1, PSO-TVW2 and PSO-TVW3 based on Equations (10) (11) and (12), are compared with the time varying inertia weight modified PSO variants listed in Table 1. Similarly the modification given in Equation (13) is added with PSO-TVW1, PSO-TVW2 and PSO-TVW3, is named as MP-PSO-TVW1 (Modified position PSO- TVW1), MP-PSO-TVW2 (Modified position PSO-TVW2) and MP-PSO-TVW3 (Modified position PSO-TVW3) respectively. The initial PSO parameters selected for simulation is given in Table 2.
The PSO variants are analyzed for linear and nonlinear channel conditions. Figure 1 exhibits the performance of different variants in linear channel and Table 3 presents it for linear and nonlinear channel conditions as stated in Equations (3), (4), (5), and (6). While comparing all PSO variants in Table 3, the proposed MP-PSO-TVW3 performs much better than other variants with minimum MSE. It shows convergence within 47 iterations and the convergence is achieved without compromising the MSE. The other proposed variants PSO-TVW1, PSO-TVW2, PSO-TVW3, MP-PSO-TVW1 and MP- PSO-TVW2 are also exhibit improved convergence rate and MSE. But the computational complexity is different. Table 3 gives the comparison and the effect of different channels with least mean square (LMS) algorithm, PSO algorithm by Shi et al. [8] , the proposed PSO-TVW2 and PSO-TVW3 for LTE and DFE structures. From Table 3 and Figure 5 to Figure 6 it is seen that the proposed modifications outperforms the other existing modifications based on convergence and MSE. The PSO-TVW3 algorithm shows best performance in all channel conditions. The LTE and DFE structures give approximately same MSE value but differ in convergence rate which is shown in Table 3.
![]()
Table 3. Comparison of convergence rate and MSE with different channel models.
![]()
Figure 5. Performance of proposed and other time varying strategies in linear channel for LTE.
![]()
Figure 6. Proposed position based PSO enhancements in linear channel for LTE.
The minimum MSE achieved by the proposed techniques are also nearly achieved by the PSO variants suggested by shi et al. [10] [11] , Chatterjee et al. [12] , and Lei et al. [15] and is given in Table 4. But these variants are lagging in convergence compared with the proposed methods.
To clearly examine the superiority of the proposed MP-PSO over all PSO variants, MP-PSO based position modification as in Equation (13) is applied to all time varying PSO variants listed in Table 1. If MP-PSO based position modification is added, it guarantees the convergence better than all PSO variants as in Table 5. Based on the simulations performed, it is observed that the MP-PSO based PSO algorithm shows guaranteed convergence within 50 iterations in all independent runs.
The proposed MP-PSO based PSO-TVW2 converges in 27th iteration to its minimum MSE −59 dB. The MP-PSO based PSO-TVW1 converges in the 45th iteration with minimum MSE of −60 dB as in Table 5. MP-PSO based PSO-TVW2 is good in convergence speed while MP-PSO based PSO-TVW1 is less in complexity. Because PSO- TVW2 needs one more division at each iteration after the intermediate iteration N, the complexity of the proposed and the other time varying variants are compared in Table 6. If position is modified based on MP-PSO, convergence is improved very fast without adding complexity. From Table 3, Figure 5 and Figure 6, it can be seen that the proposed modifications outperforms the other existing modifications in linear and nonlinear channel conditions.
To find the optimum value intermediate iteration “N”, simulations are performed for different N values and are shown in Figure 7. It is seen that if N is selected between 40
![]()
Table 4. Comparison of convergence rate and MSE OF PSO variants in LTE.
![]()
Table 5. Comparison of convergence rate and MSE of PSO variants with MP-PSO in linear channel.
and 50, it leads to optimal performance. If N is selected less than 40, MSE value is degraded and for greater values it delays the convergence.
To notify the computational complexity, all time varying inertia weight modification methods in Table 1 are compared with proposed modifications PSO-TVW1, PSO- TVW2 and PSO-TVW3. Since MP-PSO replaces the weight by the corresponding personal best weight; there is no point in addition of complexity in the algorithm. So it is not included in Table 6 for comparison. All other variants are compared and found that PSO-TVW1 has less complexity followed by PSO-TVW2. PSO-TVW1 needs m number of additions and m number of multiplications for m iterations. The variant
![]()
Table 6. Comparison of complexity of PSO variants for m number of iterations.
![]()
Figure 7. Effect of different Intermediate iteration value N on PSO-TVW2.
suggested by Zheng et al. has complexity nearer to PSO-TVW2 but its performance is poor. The proposed modifications have less complexity compared to all existing variants.
4.2. Sensitivity Analysis
The parameter values and choices of the PSO algorithm have high impact on the efficiency of the method, and few others have less or no effect. The analysis is done with respect to six key parameters namely, the intermediate iteration value N, the data window size ws, the acceleration constants ac1 and ac2, the population size P, number of tap weights T and distortion factor W. The effect of the basic PSO parameters swarm size or number of particles, window size, number of tap weights and acceleration coefficients are analyzed in [6] . The same is analyzed for PSO-TVW3 and is given in Table 7.
On average, an increase in the number of particles will always provide a better search and faster convergence. In contrast, the computational complexity of the algorithm increases linearly with population size, which is more time consuming. In Table 7, population size of 40 gives better convergence. So a problem dependent minimum population size is enough for better performance. The acceleration coefficients ac1 and ac2 control the rate at which the respective local and global optima are reached. Setting the acceleration coefficients to a minimum value slows down the convergence speed. The local search and global search are best when the summation of acceleration coefficients become ac1 + ac2 < 4 in adaptive equalization. The acceleration coefficients greater than 1 also seem to give the best performance. For equal value of acceleration constants, the algorithm converges fastest to its lowest MSE value. The MSE calculated on iterations is the average of the MSE over the window; a large window size increases the complexity per iteration and time consumption. From Table 7, window size does not make any greater changes in the MSE value. If the window size is small the complexity can be reduced.
The tap weights are problem dependent. As given in Table 7, the increase in tap weights above a certain limit does not make much difference in MSE value, but it may increase the complexity. Figure 7 shows the analysis for different intermediate iteration N for PSO-TVW2. Table 8 compares the convergence rate and MSE for PSO-TVW2 and PSO-TVW3 with reference to N. An increase in the value of N increases the number of iterations required for convergence. Decreasing N value degrades the MSE performance. The N value between 30 and 40 exhibits minimum MSE with faster convergence.
Table 9 explains the effect of amplitude distortion parameter W in linear channel.
![]()
Table 7. Effect of PSO parameters on Pso-Tvw3.
![]()
Table 8. Comparison of convergence rate with different intermediate iteration value N.
![]()
Table 9. Effect of amplitude distortion W on PSO-TVW2 for LTE and DFE.
The MSE is computed with different amplitude distortion that leads to different eigen value spread. An increase in amplitude distortion degrades the MSE performance. The performance degradation is not severe in proposed PSO based algorithms compared to existing algorithms. The MSE performance of DFE is better than the LTE structure. But the number of iterations required for convergence is less in LTE compared to DFE except for PSO-TVW2.
5. Conclusion
In this work, an enhanced PSO based channel equalization is proposed to improve convergence and mean square error of equalizer for adaptive equalization. The proposed time varying PSO algorithms, PSO-TVW2, PSO-TVW3 and MP-PSO improve the convergence speed much better than other existing variants in linear and nonlinear channels. All the existing PSO variants have improved convergence speed when enhanced with position based modification MP-PSO. MP-PSO based PSO-TVW1 is less in complexity and MP-PSO based PSO-TVW2 is fast in convergence. The proposed modifications reduce the computational complexity and also increase the convergence speed without compromising the MSE. Also the convergence is guaranteed within 50 iterations for all independent runs.