Asymptotically Antiperiodic Solutions for a Nonlinear Differential Equation with Piecewise Constant Argument in a Banach Space

William Dimbour¹, Vincent Valmorin²

¹UMR Espace-Dev Université de Guyane, Cayenne, Guyane.
²Laboratoire C.E.R.E.G.M.I.A. Université des Antilles, Pointe-à-Pitre, Guadeloupe.

DOI: 10.4236/am.2016.715145                

Abstract

In this paper, we give sufficient conditions for the existence and uniqueness of asymptotically w-antiperiodic solutions for a nonlinear differential equation with piecewise constant argument in a Banach space when w is an integer. This is done using the Banach fixed point theorem. An example involving the heat operator is discussed as an illustration of the theory.

Keywords

Asymptotically ω-Antiperiodic Functions, Differential Equations with Piecewise Constant Argument, Semi-Group

1. Introduction

We are concerned with the differential Cauchy problem with piecewise constant argument:

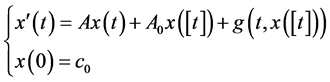(1)

where 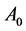is a bounded linear operator, 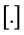is the largest integer function, g is a continuous function on 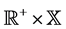and A is the infinitesimal generator of an exponentially semigroup 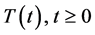acting on the Banach space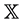. The main purpose of this work is to study, for the first time, the existence and the uniqueness of asymptotically w-anti- periodic solutions to (1) when w is an integer.

Differential equations with piecewise constant argument (EPCA) have the structure of continuous dynamical systems in intervals of constant length. Therefore they combine the properties of both differential and difference equations. They are used to model problems in biology, economy and in many other fields (see [1] - [7] ).

Recently, the authors of [18] introduced the concept of asymptotically antiperiodic functions and studied semilinear integrodifferential equations in this framework. In [19] , a new composition theorem for asymptotically antiperiodic functions is proved. This result is used to show the existence and the uniqueness of asymptotically antiperiodic mild solution to some fractional functional integro-differential equations in a Banach space. Motivated by [18] and [19] , we will show the existence and uniqueness of asymptotically antiperiodic mild solution for (1).

This work is organized as follows. In Section 2, we recall some fundamental properties of asymptotically antiperiodic functions. Section 3 is devoted to our main results. We illustrate our main result in Section 4, dealing with the existence and the uniqueness of asymptotically antiperiodic solution for a partial differential equation.

2 Preliminaries

Let 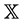be a Banach space. The space 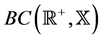of the continuous bounded functions from 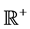into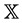, endowed with the norm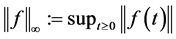, is a Banach space. The Banach subspace of functions f such that 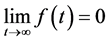is denoted by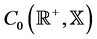. A positive number w being given, 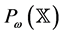will be the subset of 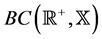constituted of all w-periodic functions; it is also a Banach space. We recall the following properties of antiperiodic and asymptotically antiperiodic functions. We refer to [18] where they are proved.

Definition 2.1. A function 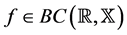is said to be w-antiperiodic (or simply antiperiodic) if there exists 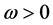such that for all. The least such w will be called the antiperiod of f.

We will denote by, the space of all w-antiperiodic functions.

Theorem 2.1. Let. Then the following are also in.

i), , c is an arbitrary real number.

ii), provided on. Here.

iii), a is an arbitrary real number.

Theorem 2.2. is a Banach space equipped with the supnorm.

Now we consider asymptotically w-antiperiodic function.

Definition 2.2. A function is said to be asymptotically w-antiperiodic if there exist and, such that

g and h are called respectively the principal and corrective terms of f.

We will denote by, the space of all asymptotically w-antiperiodic - valued functions.

Remark 2.1. is a Banach space equipped with the supnorm and the decomposition of an asymptotically antiperiodic is unique.

3. Main Results

We begin with the definition of a solution to (1).

Definition 3.1. A solution of Equation (1) on is a function x(t) that satisfies the conditions:

1-x(t) is continuous on.

2-The derivative exists at each point, with possible exception of the points where one-sided derivatives exists.

3-Equation (1) is satisfied on each interval with.

Let be the semigroup generated by A and x a solution of (1). Then the function m defined by is differentiable for and we can write:

which leads to

(2)

The function is a step function and is a continuous function in the intervals, where. Therefore, the functions and are integrable over with. Integrating both sides of (2) over, yields

Therefore, we give the following

Definition 3.2. Let be the semigroup generated by A. The function given by

is the mild solution of the Equation (1).

Now we assume that:

(H.1) The operator A is the infinitesimal generator of an exponentially stable semigroup such that there exist constants and with

The proof of the main result of this paper is based on the following two lemmas.

Lemma 3.1. Assume that (H.1) is satisfied and that is a linear bounded operator. Let, we define the nonlinear operator by: for each

Then the operator maps into itself.

Proof. Define the function F by

Since, it may be decomposed as holds, where and. We note that

where

and

We claim that. Since, then. Therefore:, there exists a constant such that for all. For all, we have that

from which it follows that

Hence,. Since H is clearly continuous, the claim is then proved. Now, we show that:

Therefore. It follows that and which proves that. ,

Lemma 3.2. Assume that (H.1) is satisfied and also that. Let be such that:

i);

ii).

Define the nonlinear operator by: for each

Then the operator maps into itself.

Proof. Let. Then with and. We have

with. We have

Since, we deduce that.

We note also that. In fact

We put

Since the function g is lipschitzian, then the function is piecewise continuous. Therefore the function F is well defined. Since with and, we observe that

where

and

The functions and are well defined because the function and are continuous on where n is an integer. Since and, it follows that and . ,

Now we can state and prove the main result of this work.

Theorem 3.3. We assume that the hypothesis (H.1) is satisfied. We assume also that. Let such that:

i)

ii).

Then the Equation (1) has a unique asymptotically antiperiodic solution if

Proof. Define the nonlinear operator,

for every, where

and

Since we have. Then, using Lemma 3.1 and Lemma 3.2, it follows that the operator maps into itself.

For every,

Therefore, since, using the Banach fixed point Theoren we conclude that Equation (1) has a unique asymptotically w-antiperiodic solution. ,

4. Application

As an application, consider for and, the Cauchy problem:

(3)

We take and we define the linear operator A by

i),

ii).

Note that such a function exists. Take for instance where f is a w-periodic function from into. Then we have

and

Theorem 4.1. We assume that. Then System (3) has a unique asymptotically w-antiperiodic if

Proof. We have, , and we apply Theorem 3.3. ,

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Shah, S.M. and Wiener, J. (1983) Advanced Differential Equations With Piecewise Constant Argument Deviations. International Journal of Mathematics and Mathematical Sciences, 6, 671-703. http://dx.doi.org/10.1155/S0161171283000599
[2]	Van Minh, N. and Tat Dat, N. (2007) On the Almost Automorphy of Bounded Solutions of Differential Equations with Piecewise Constant Argument. Journal of Mathematical Analysis and Application, 326, 165-178. http://dx.doi.org/10.1016/j.jmaa.2006.02.079
[3]	Wiener, J. (1999) A Second-Order Delay Differential Equation with Multiple Periodic Solutions. Journal of Mathematical Analysis and Application, 229, 6596-676. http://dx.doi.org/10.1006/jmaa.1998.6196
[4]	Wiener, J. and Debnath, L. (1997) Boundary Value Problems for the Diffusion Equation with Piecewise Continuous Time Delay. International Journal of Mathematics and Mathematical Sciences, 20, 187-195. http://dx.doi.org/10.1155/S0161171297000239
[5]	Wiener, J. and Debnath, L. (1995) A Survey of Partial Differential Equations with Piecewise Continuous Arguments. International Journal of Mathematics and Mathematical Sciences, 18, 209-228. http://dx.doi.org/10.1155/S0161171295000275
[6]	Wiener, J. and Lakshmikantham, V. (1999) Excitability of a Second-Order Delay Differential Equation. Nonlinear Analysis, 38, 1-11. http://dx.doi.org/10.1016/S0362-546X(98)00245-4
[7]	Wiener, J. (1993) Generalized Solutions of Functional Differential Equations. World Scientific, Singapore, New Jersey, London, Hong Kong.
[8]	Henríquez, H.R., Pierre, M. and Táboas, P. (2008) On S-Asymptotically ω-Periodic Function on Banach Spaces and Applications. Journal of Mathematical Analysis and Applications, 343, 1119-1130. http://dx.doi.org/10.1016/j.jmaa.2008.02.023
[9]	Henríquez, H.R., Pierre, M. and Táboas, P. (2008) Existence of S-Asymptotically ω-Periodic Solutions for Abstract Neutral Equations. Bulletin of the Australian Mathematical Society, 78, 365-382. http://dx.doi.org/10.1017/S0004972708000713
[10]	Liu, Y. and Liu, X. (2013) New Existence Results of Anti-Periodic Solutions of Nonlinear Impulsive Functional Differential Equations. Mathematica Bohemica, 138, 337-360.
[11]	Al-Islam, N.S., Alsulami, S.M. and Diagana, T. (2012) Existence of Weighted Pseudo Anti-Periodic Solutions to Some Non-Autonomous Differential Equations. Applied Mathematics and Computation, 218, 6536-6648. http://dx.doi.org/10.1016/j.amc.2011.12.026
[12]	Alvarez, E., Lizama, C. and Ponce, R. (2015) Weighted Pseudo Antiperiodic Solutions for Fractional Integro-Differential Equations in Banach Spaces. Applied Mathematics and Computation, 259, 164-172. http://dx.doi.org/10.1016/j.amc.2015.02.047
[13]	Chen, H.L. (1996) Antiperiodic Functions. Journal of Computational Mathematics, 14, 32-39.
[14]	Chen, Y.Q. (2006) Anti-Periodic Solutions for Semilinear Evolution Equations. Journal of Mathematical Analysis and Applications, 315, 337-348. http://dx.doi.org/10.1016/j.jmaa.2005.08.001
[15]	Freire, J.G., Cabeza, C., Marti, C., Pöschel, T. and Gallas, J.A.C. (2013) Antiperiodic Oscillations. Scientific Reports, 3, Article Number: 1958. http://dx.doi.org/10.1038/srep01958
[16]	Haraux, A. (1989) Anti-Periodic Solutions of Some Nonlinear Evolution Equations. Manuscripta Mathematica, 63, 479-505. http://dx.doi.org/10.1007/BF01171760
[17]	Okoshi, H. (1990) On the Existence of Antiperiodic Solutions to a Nonlinear Evolution Equation Associated with Odd Subdifferential Operators. Journal of Functional Analysis, 91, 246-258. http://dx.doi.org/10.1016/0022-1236(90)90143-9
[18]	N’Guérékata, H. and Valmorin, V. (2012) Antiperiodic Solutions of Semilinear Integrodifferential Equations in Banach Spaces. Applied Mathematics and Computation, 218, 11118-11124. http://dx.doi.org/10.1016/j.amc.2012.05.005
[19]	Mophou, G., N’Guérékata, G. and Valmorin, V. (2013) Asymptotic Behavior of Mild Solutions of Some Fractional Functional Integro-Differential Equations. African Diaspora Journal of Mathematics, 16, 70-81.
[20]	Diagana, T. and N’Guérékata, G.M. (2007) Almost Automorphic Solutions to Some Classes of Partial Evolution Equations. Applied Mathematics Letters, 20, 462-466. http://dx.doi.org/10.1016/j.aml.2006.05.015