Hidden Markov Models to Estimate the Lagged Effects of Weather on Stroke and Ischemic Heart Disease ()
Received 15 June 2016; accepted 1 August 2016; published 4 August 2016
1. Introduction
The association between low temperature and morbidity of disease is well recognized (e.g., [1] [2] ). The exact mechanism of this association is not described well. In this direction, to estimate the length of the lag period (delay) between exposure to temperature and its effect on the onset of diseases becomes important.
Many works have been done to clarify the lagged effects, and most of them used Poisson regression model with certain spline functions or some smoothing technique. This direction resulted to neglect all of the extreme cases in order to get “stochastically significant” correlation.
For example, in [3] , lagged effects of 3 to 5 days for hot temperature were observed for respiratory and cardiovascular deaths in 12 U.S. cities. They used smooth functions for distributed lag model. The shape of the mortality-temperature relation was examined by fitting cubic spline models ( [4] ). In [5] , daily temperatures and daily mortality on successive days before and after a reference day were regressed on the temperature of the reference day using high pass filtered data. The increases in deaths were maximal at 3 days after the peak in cold for IHD (Ischemic Heart Disease), at 12 days for RES (Respiratory Disease), and at 3 days for all cause mortality. Poisson regression and distributed lag models were used with a cubic regression spline of apparent temperature in [6] .
Thus, many works used Poisson regression model with certain smoothing functions to address the lagged effects. These methods inevitably neglected the existence of extreme case as exceptional cases or as random noise. However, such exceptional cases (e.g. combination of a rise in temperature and an increase in risk) were recognized to be important and not negligible for cerebral infarction by [7] and for ischemic heart disease by [8] . Therefore, the effects of lags must be estimated by models without use of regression models with spline functions. For this purpose we proposed, in this paper, a new method, i.e., Hidden Markov Models by Self- Organized Maps (HMM by SOM).
2. Method
2.1. Data
This study was carried out for the data from Nagoya city, Japan. Its population is over 2,260,000 inhabitants. It is situated in the middle of Japan, facing the Pacific Ocean. The climate in the city is that known as a typical mild Japanese climate, representing the change of four seasons.
The daily number of patients was obtained from Nagoya City Fire Department. The data contained the number of patients who were first transported by ambulance to a hospital and then diagnosed, at the hospital, as cerebral infarction, ischemic heart disease, myocardial infarction, angina pectoris and so on. The data contained all ages. These data was taken among two periods. One was from 2002 to 2005 and the other from 2009 to 2012.
As for meteorological data, we selected a daily data supplied by Japan Meteorological Agency. The data consisted of temperature (mean, maximum and minimum temperature) and the hours of sunshine and so on.
2.2. Self-Organized Map (SOM)
Self-Organizing Map (SOM) is a kind of “cluster mapping”, and was first introduced by [9] . It gives us an overview of multivariate data sets (called input layer), and supplies visualization on graphical map displays (called target layer). See [11] [12] for the details of application of SOM to the problem of links between diseases and weather.
SOM uses artificial neural networks to find a continuous mapping from input space or layer to a target layer or lattices in two-dimensional space. These lattices are considered as “neurons”. These points in lattices in plane were also called “units”. The map was realized so that as much as possible of the original structure of the measurement vectors in the n-dimensional space are to be conserved in lattice structure in plane. As a result, if the points in original data are “near” (or “distant”), then they were mapped to “near” (or “distant”) units in plane. Thus SOM visualizes cluster tendency of the data.
2.3. Hidden Markov Model (HMM)
A hidden Markov model was a tool for representing random change of states over time series of observations. The method was applied broadly to many fields, for example, to DNA profiles ( [12] ) and to a statistic model for precipitation ( [13] ). Here in this paper, observation data were supposed to be the daily data of numbers of patients of cerebral infarction or ischemic heart disease, transported by ambulance in Nagoya city.
The “states” in HMM were considered as a representation of a process in “background”. One can suppose there was a sort of “background” even for the incidence of diseases. Here we supposed that such background states were a kind of randomly changing weather states. In this article, such states were given by the classification due to Self-Organized Map (SOM) which was applied to meteorological elements. This idea realized the links between the change of weather patterns and the change of the risk of cerebral infarction and ischemic heart disease. For basic elements of HMM, see [14] in general or [10] [11] for this field of application.
3. Results
3.1. Results by Self-Organized Map (SOM)
In this article, SOM was carried out to the daily data of eight weather elements (such as maximum temperature, minimum temperature, precipitation, humidity, local pressure, wind velocity, the hours of daylight and solar radiation) in Nagoya city. The data were supplied by Japan Meteorological Agency and were collected during two periods, i.e., from 2002 to 2005 and from 2009 to 2012. Here we used the so-called “standard” SOM, based on unsupervised neural learning algorithms. The obtained units or classes were used as the states of Hidden Markov Models (described later).
As a target layer, lattices of 3 times 2 units (totally 6 units) were selected. Thus, we obtained our classification of meteorological data to just six classes of “weather states”. See Figure 1, where the classified classes were denoted by (a)-(f). The range of the scales varied from 0 to 1, because all the data were scaled so as to have mean 0 and variance 1. In Figure 1, the classes were roughly divided into two groups: (a) (b) were the group of high pressure of local atmosphere, and (c)-(f) were the group of low pressure. The group of high pressure was further divided into two classes: the class (a) was a type of warm weather with high pressure, and (b) a type of cold weather with high pressure. The low pressure group was divided into four classes: the class (c) expressed cold and windy weather, (d) rainy weather, (e) warm weather and (f) humid weather.
Thus these six classes were named “(a) high pressure (warm), (b) high pressure (cold), (c) low pressure (cold, windy), (d) low pressure (rainy), (e) low pressure (warm), and (f) low pressure (humid)”, according to the character of each class.
3.2. Hidden Markov Model
HMMs consist of two kinds of elements: one is the set of “states”, the other is series of “observation”. Both “states” and “observations” change randomly as times go by and the “states” were supposed to generate “observations” by some mechanism.
To understand links between the incidence of diseases and the weather, the variability of weather could be thought as a s “background” bringing the incidence of diseases such as stroke incidence and ischemic heart disease. Here we supposed that such background states of weather changed randomly and formed a set of states in HMM. The “states” were those classes obtained by the above SOM which express six weather patterns; “high pressure (warm), high pressure (cold), low pressure (cold, windy), low pressure (rainy), low pressure (warm), and low pressure (humid)”.
The “observation” was the daily data of numbers of patients who were once transported by ambulance in Nagoya city and were diagnosed later as cerebral infarction or ischemic heart diseases.
The observation at time t(day)is represented by the variable R(t) (the number of patients). The observation R(t) at time t is generated randomly by some process whose state S(t) (one of the six weather states given by SOM). HMM assumes that the state S(t) is determined randomly from the state S(t − 1) of the previous day. Both random processes are assumed to be Markov process. See Figure 2.
Each state is supposed to change to another state with some probability. The collection of all of these probabilities formes a “Transition Matrix” P, where j-th state changes to i-th state with probability Pij. Each state (e.g., j-th state) at time t generates an observed value, according to some distribution Qj. The collection of such distribution formes a “distribution matrix” Q, where j-th column of Q is equal to Qj. As a consequence, we have a set
,
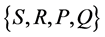where S and R are the sets of states and observation. This set defines a Hidden Markov Model. We calculated
![]()
![]()
Figure 1. The results of SOM; six patterns of weather states.
these two matrices P and Q by analyzing the data from 2002 January to 2004 December, and also from the data from 2009 to 2012, separately. See for details [12] .
3.3. How to Find Lags
Cold exposure is not generally associated with an immediate increase of patients or death with respect to cerebral
![]()
Figure 2. Sequences of states and observations in a hidden Markov model without delay.
infarction and ischemic heard disease. There appears to be some interval between the incidence of temperature change and the onset of these diseases. Such interval is called “lag” or “delay”.
Many studies used Poisson regression and distributed lag models. In this article, we applied our hidden Markov model to find “lag” or “delay”. For this purpose, hidden Markov model was shifted according to the amount of delay. This procedure was illustrated by the comparison of Figure 2 and Figure 3.
Figure 2 showed the non-shifted normal hidden Markov model (with delay = 0) with six states of weather patterns (classified by SOM). The observed value R(t) corresponds to the state S(t). Figure 3 described “shifted” HMM. The amount of shift was equal to “delay” (equal to 1 in this figure). For general delay d, the observed value R(t) corresponds to the state S(t − d).
To estimate the “lag”, the simulation was carried out for several times (500 or 1000 times) for this shifted hidden Markov model for the given delay. The comparison between the original observed values and these simulated sequences was performed by calculating the root mean square errors (RMSEs) of these two sequences. We first fixed the delay = d (days) and considered shifted HMM of delay d. Then, starting from certain day (e.g. 15-th of January in 2005), we let the HMM generate simulated sequences of the risk R(t) during T days:
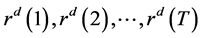
Here, T was taken to be equal to one of the numbers 3, 5 or 7 days.
We compared this simulated sequence with the original sequence of the number of patients:
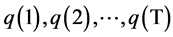
and calculated the Root Mean Square Error of these two sequences:
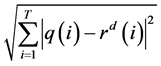
We repeated this process 500 times to get the 500 sequences of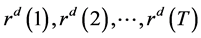 
and the corresponding RMSEs. By taking the average of these RMSEs, we thus associated the delay d with the mean of RMSEs. If we make delay d to vary like
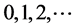, and collect the corresponding values of RMSE, then we get the graph of RMSE versus delay d.
For example, in Figure 4, we had the graph of RMSE versus lagged days in winter for cerebral infarction. Simulations were performed during 3 days and 5 days from 15-th of January 2005. RMSEs were the mean of RMSEs during winter season.
The next example was described in Figure 5. Here, the graph of RMSE versus lagged days was calculated for summer and the other conditions were supposed to be same as Figure 4. Again, the delay of 3 days was observed.
The calculations of RMSE versus delay were similarly performed for the data from 2009 to 2012 with respect to the incidence of both Cerebral Infarction (CI) and Ischemic Heart Disease (IHD). We fixed the month, and
![]()
Figure 3. Shifted hidden Markov model with delay of one day, i.e., d = 1. Here, the weather state of time t affects the risk of the next day t + 1.
![]()
Figure 4. The graph of RMSE between simulations and observed data (cerebral infarctions) versus lagged days in winter. Simulations began from 15-th of January 2005, The duration T was taken to be 3 days or 5 days. Here, the delay of 2 or 3 days was observed.
calculated transition matrix and distribution function looking at all the months from 2009 to 2012. Then we constructed the HMM by the transition matrix and distribution. By shifting this HMM according to each delay, we could get the graphs of RMSE versus delay for each month. The results were illustrated in Figure 6 for cerebral infarction and in Figure 7 for ischemic heart disease.
The existence of lags was shown by both graphs. The lags of 4 - 6 days were observed for the months, January, February, March, April, August, October and December for CI. The lags of 2 - 6 days were observed for the months, January, February, April, June, July, August, September, November and December for IHD.
The 4 - 6 days of delay were observed for the months 1, 2, 3, 4, 8, 10, 11 and 12. No delay was found for the months 5, 6, 7 and 9.
The 2 - 6 days of delay were observed for the months 1, 2, 4, 6, 7, 8, 9, 11 and 12. No delay was found for the months 3, 5 and 10.
![]()
Figure 5. The graph of RMSE versus lagged days in summer, from 2002 to 2005. The duration T was taken to be 3 days or 5 days.
![]()
Figure 6. The graphs of RMSE versus delay (days) plot for all months from 2009 to 2012, for cerebral infarction.
![]()
Figure 7. The graphs of RMSE versus delay (days) plot for all months from 2009 to 2012, for ischemic heart disease.
3.4. Stochastic Significance
The t-test and Wilcoxon-test were used to test the stochastic significance of the existence of lagged effects. To illustrate this process, we selected, for example, the case of cerebral infarction in August from 2009-2012 from Figure 6, and described it as Figure 8.
The lag of 4 days was observed in Figure 8. By setting d = 4, we calculated RMSEs of 500 sequences of simulated series of risk, during five days from 15-th of August in 2012. For the delay d = 0, we similarly got 500 RMSEs. Thus we had two groups of RMSEs. We compared these RMSEs of two groups and tested whether the difference of RMSE (more precisely the square of RMSE) was stochastically significant. The result was described in Table 1. Both t-test and Wilcoxon-test assured the stochastic significance. The stochastic significance of the existence of lags was assured for our HMM by SOM.
4. Discussion
The lagged effects of weather state on the onset of cerebral infarction (CI) and ischemic heart disease (IHD) were investigated using shifted hidden Markov model with weather states given by self-organized maps. We found the delay of 2 - 6 days both for CI and IHD. The existence of delay was examined by the graphs of root mean squared error (RMSE) versus delay. The stochastic significance of the existence of delay was assured by t-test and Wilcoxon-test.
![]()
Figure 8. RMSE versus delay (days) in August from 2009 to 2012, extracted from Figure 6.
![]()
Table 1. p-values of t-test and Wilcoxon. Test for the comparison of RMSE of delay = 0 with that of delay = 5 by Hidden Markov Model for cerebral infarction during December from 2009 to 2012.
4.1. Comparison with Regression Models
The existence of delay was already well-known, but most of researchers used regression models by excluding exceptional cases as noise and by smoothing with spline functions. The present paper proposed a use of hidden Markov models with weather states as a new method for this direction.
To compare regression models and our HMM, we performed to calculate the lagged effects by usual Poisson regression models. For this purpose, we selected “Residual standard error (RSE)” which were the standard index of errors for auto-regression models. Figure 9 showed Residual Standard Error versus delay for August from 2009 to 2012 with respect to cerebral infarction.
The delay of 3 - 4 days was seen from Figure 9. It might appear rigorous at first glance. However, if we focused on stochastic significance of auto-regressions themselves, we observed that all the coefficients of mean temperature failed to reduce effective p-values with resect to all the values of delay. See Table 2.
This result showed that regression models were not statistically significant if they did not use the spline or smoothing function, whereas our HMM included exceptional cases as randomness innature, which had been excluded by regression model.
4.2. The Mechanism of Delay
In [15] , they examined data in England and Wales and found that the temperature over the previous 3 - 4 days was relevant in deaths caused by cerebrovascular accident, and that temperature over the previous 2 days was of most critical relevance for deaths due to myocardial infarction. They suggested that cold exposure resulted an increase in arterial blood pressure and platelet viscosity.
![]()
Figure 9. The plot of RSE (Residual standard error) versus delay by the regression model for the data in August from 2009 to 2012.
![]()
Table 2. The p-values of poisson auto-regression in August, from 2009 to 2012 for each delay 0, 1, ・・・, 7.
In [16] , a positive effect of cold on blood pressure was described. The blood pressure became 3 - 5 mm Hg higher in the coldest month. There was seen the association to fibrinogen and thrombosis. They found significant increases in platelet counts, neurophil counts, plasma and whole blood viscosity. The most striking effect of cold seemed to be on plasma fibrinogen concentration.
In [17] , they showed that the exposure to cold in young healthy subjects caused changes in hematological factors known to be associated with the promotion of thrombo-genesis. The cold exposure was associated with an increase in plasma viscosity, leading increase in the risk for thrombosis. They observed also that cold exposure induced increases of hematocrit and brought the fluid loss from plasma which resulted hemo-concentration. Cold exposure might be responsible for initiating a mild inflammatory response.
All these evidences suggest that cold exposure does not direct the onset of CI or IHD immediately, and that it needs more time to lead to the thrombosis through the state of increase of plasma and whole blood viscosity.
5. Conclusion
In conclusion, our hidden Markov model is more natural than regression model to assess the lagged effects of weather states on the incidence of cerebral infarction and ischemic heart disease. While regression models are not statistically significant without use of spline or smoothing functions, our hidden Markov model encompasses exceptional cases (as random possibility) which were excluded normally by regression models. Our HMM could show the existence of lags for the effect of weather changes on cerebral infarctions and ischemic heart disease. This finding may make it possible to take precautionary measures against the fatal outcome after heat shock including cold exposure.