Subject Areas: Particle Physics
1. Introduction
Thermodynamical properties, like entropy and temperature, of black holes have been established about four decades ago [1] [2] . More recently thermodynamics has been considered as the major agent behind general relativity by Padmanabhan [3] . Thermodynamical concepts have been applied to black holes as well as to local Rindler, or acceleration, frames [4] . This analysis has indicated that the vacuum state of even Minkowski space has observer dependent temperature [5] and particle content. In [6] acceleration frame considerations have been applied to a model of stretched horizon black holes by calculating the partition function of the system.
I describe first a warmup model for the structure of quantum black holes. The black hole horizon is a spherical membrane covered with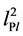 
size squares, each of which can be in k states. The membrane dynamics is represented by a two dimensional harmonic oscillator.
Secondly, I redefine the membrane partition function as a sum over black hole stretched horizon constituents based on [6] . This method gives as predictions of Hawking radiation and Bekenstein-Hawking entropy. The author regards the stretched horizon black holes as atoms of spacetime. I propose here that the structure of black holes is the same as the structure of spacetime atoms. An attempt for unified quantum picture for both spacetime and matter is proposed using a preon model by this author.
Large amounts of results of research by the various schools of thought towards quantum gravity are widely scattered around in various journals in the literature, see e.g. [7] [8] . The motivation of this note is to compile together some of them, as I see appropriate, from the point of view of physics, with some thoughts of mine.
This note is organized as follows. The presentation is very concise in all sections. After the Introduction the simple oscillator model for black holes is described in Section 2. In Section 3 I present the main points of the stretched horizon black hole model. An attempt for consistent quantization of spacetime and matter is discussed in Section 4 in connection with a model for composite quarks and leptons. Finally in Section 5 I give a brief discussion of results and conclusions.
2. Membrane Model of Horizon
As the first model for black holes of any size I assume the standard picture of a hole as a spherical horizon covered with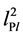 
size squares. The minimal horizon radius is of the order of
. All physics takes place on the surface of the sphere, and tentatively, none inside. Suppose there are n squares on the horizon and each square can be in k soft hair states [9] . Then the total number of states is
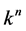. This gives for entropy S of the sphere the well known result
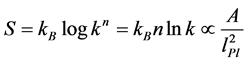(1)
where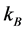 
is the Boltzmann constant and A is the area of the horizon.
The vibrations of an oscillator can be calculated in normal way, with certain frequency restrictions due to the grid. The geometry is a two dimensional sphere
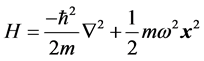(2)
The energy eigenvalues for a square are given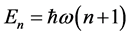 
where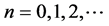
.
The partition function Z is (to be used in section 5)
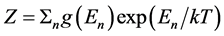(3)
where 
(=k in (1)) is the degeneracy of the n’th state and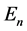 
its energy and T the temperature.
3. Model of Stretched Horizon
I consider a micro black hole dressed by a (virtual reality [10] ) stretched horizon, which is a membrane hovering about a Planck length outside the event horizon and which is both physical and hot. A treatment of the stretched horizon has been done by Mäkelä in [6] which paper I cite below. He assumes that the stretched horizon consists of finite number of discrete constituents each contributing to the stretched horizon an area of a non-negative integer times a constant
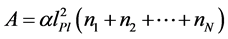(4)
where n is the number of constituents, the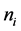 
define their area quantum states and 
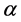is a number of the order unity, to be determined later. For the constituents themselves one assumes simply black holes of size![]()
. It is supposed that each stationary quantum state of a black hole is determined by the quantum numbers ![]()
of its stretched horizon. Other candidate constituents are Planck scale strings, scalar fields or, very likely, graviton configurations.
To calculate the partition function of a Schwarzschild black hole one needs to know the energy levels of the system. The energy of the hole from the point of view of an observer on its stretched horizon is called Brown- York energy [11]
![]()
(5)
where a is the constant proper acceleration of an observer on the stretched horizon and A is the area of the horizon. The possible energy values of a black hole are, from the point of view of an observer located on its stretched horizon, in terms of the acceleration
![]()
(6)
where![]()
. The number of microscopic states associated with energy ![]()
is the number of ways of writing a given positive integer n as a sum of exactly n positive integers, with![]()
, which is given by the binomial coefficient
![]()
(7)
It depends on n and N only1, and it gives the degeneracy function![]()
. The degeneracy of a state with energy ![]()
is
![]()
(8)
whenever![]()
. If![]()
, we have
![]()
(9)
If![]()
, ![]()
is simply the number of ways of expressing n as a sum of positive integers, no matter how many. Since the maximum number of those positive integers is n, we find that ![]()
is given by Equation (9), whenever![]()
.
The resulting partition function ![]()
of the Schwarzschild black hole may be calculated explicitly from (3), (6), (8) and (9)
![]()
(10)
where
![]()
(11a)
![]()
(11b)
where
![]()
(12)
The lengthy calculation yields a simple expression [6] :
![]()
(13)
and the temperature ![]()
is called the characteristic or critical temperature of the hole.
From the partition function one can calculate the average energy
![]()
(14)
of the hole at temperature ![]()
which yields
![]()
(15)
The average energy per constituent is
![]()
(16)
and one gets for large N
![]()
(17)
where
![]()
(18a)
![]()
(18b)
where ![]()
has been used.
It is shown in [6] that when ![]()
the average energy per a constituent of the stretched horizon is, in SI units,
![]()
(19)
and that
![]()
(20)
where ![]()
denotes the terms, which are of the order![]()
, or less. When the number N of constituents becomes large increase of energy does not change the temperature of the hole at![]()
. So the hole undergoes a phase transition at![]()
.
The most important implication of the observed phase transition at the characteristic temperature ![]()
is that it predicts the Hawking effect: the result that ![]()
is practically zero, when![]()
, and then suddenly jumps by the latent heat![]()
, when![]()
, the characteristic temperature ![]()
is the lowest possible temperature a black hole may have. If the temperature T of the black hole were less than its characteristic temperature![]()
, all of the constituents of its stretched horizon, except one, would be in vacuum, and there would be no black hole.
With some more effort one can obtain the Bekenstein-Hawking entropy law for the Schwarzschild black hole from its partition function which, in turn, followed from the specific microscopic model of its stretched horizon [6]
![]()
(21)
When![]()
, the energy of the hole from the point of view of an observer on its stretched horizon is exactly
![]()
(22)
It is interesting that, up to an unimportant numerical factor![]()
, this expression for energy is the same as the one used as a starting point in the scenario for an entropic theory of gravity in [12] .
How do we interpret the stretched horizon model? It applies both to black holes and atoms of spacetime. The next question is: are matter particles pointlike in this spacetime or do particles have some kind of substructure? In a unified model both spacetime and matter particles have the same type of substructure as we see in the next section.
4. Unified Model of Spacetime and Matter
Statistical methods of section 3 for spacetime offer a possibility to study the matter sector from a novel point of view for an attempt to build a consistent, unified statistical picture of both spacetime and matter. This goal would imply some internal structure at scale of the order of ![]()
for particles. Such a model has been proposed in [13] (though there never was experimental support for it).
The basic idea in [13] is that the quarks and lepton are made of maxons with charge 0 or ![]()
and “color” (i, j, k) as permutation index as follows
![]()
(23)
The construction (23) on maxon level is matter-antimatter symmetric and 'color' singlet, which is desirable for early cosmology.
The maxons are black holes [13] with stretched horizons. To get the standard model particles the problem of large mass difference between the Planck mass and particle masses has to be explained. It is accomplished from (4) by setting![]()
, which leads by (5) to zero, or a low mass remnant of the hole. However, this maxon, without stretched horizon, may interact with the Higgs field and gain additional mass from it. I assume now that the standard model quarks and leptons are bound states of maxons with the Higgs, or other scalar mediating the binding. The question of existence of free single maxons together with a scalar field is postponed to another study (see also [8] [14] ). It may be a new particle or it can also be assumed that some kind of confinement is operating.
The gauge bosons and the Higgs would be elementary (but their composite nature is not ruled out). The three generations would be due to a gravitational mechanism or a new symmetry. Missing at the moment are calculational methods for the bound states. Numerical methods can usually be developed at some level of accuracy.
5. Discussion and Conclusions
If a non-inertial observer perceives a horizon, he will attribute to it the Davies-Unruh temperature
![]()
(24)
where ![]()
is the acceleration of the observer. This result makes the notion of temperature and all of thermodynamics observer dependent phenomena. This problem was taken into account by the local Rindler frame procedure in the earlier sections.
It has turned out that horizons have profound importance in gravity both on thermodynamical and statistical levels. There are interesting questions of heat as inertial effect in a quantum equivalence principle and static observer’s virtual reality in [10] .
In the UV black holes cannot be probed deeper than![]()
. With increasing energy the hole begins to grow approaching the classical regime. This model is therefore consistent with the concept of self-completeness [15] .
The regime of real quantum gravity is limited to the vicinity of mini black holes and very early universe. Otherwise classical theory is accurate.
A model of decay and radiation of black holes has been proposed in [16] [17] . The lightest black hole state![]()
, the remnant or gravon, is expected to decay into standard model particles. Otherwise black holes radiate by the Hawking mechanism and by a classical no-hair theorem based mechanism producing non-thermal particles, dominantly light leptons.
There are at present a number competing theoretical schemes for quantum gravity like string theory, loop quantum gravity, causal dynamical triangulation, and others. The model of Section 3 goes deep into the structure of the physical universe and can be considered as a promising candidate. In that scenario the horizon properties of black holes and local Rindler frames are the origin of gravity and general relativity is its IR limit. These ideas have also been applied to the matter sector in connection of a preon model in Section 4.
The results of this simple model can be considered encouraging for the development of a more realistic model. A more involved model for the stretched horizon should include gravitons and is expected to produce a smoother transition for the system in getting down from Planck scale down to standard model particle mass scale. Finally, this note is a program definition for future work with a number of model results as guidelines.